Что такое пятая часть в математике

Обыкновенные дроби

Доли единицы

Единицу можно разделить на равные части.

Пример. Изобразим единицу отрезком и разделим его на три равных части:

Каждую из этих равных частей, на которые разделена единица, называют долей единицы, долей целого или просто долей.

Доля единицы — это каждая из равных частей, на которые разделена единица.

При делении единицы на равные части, доли получают название, которое зависит от того, на сколько частей была разделена единица.

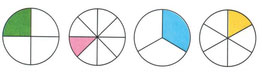
Пример. Если единица разделена на 5 равных частей, то каждая доля называется пятой (частью), а все вместе — пятые (части):

Название доли указывает, какая это часть единицы, а также даёт понять, на сколько равных частей была разделена единица.

Обыкновенные дроби

Для описания количества долей используются обыкновенные дроби.

Обыкновенная дробь — это число, выражающее количество долей. Обыкновенная дробь иначе называется простой дробью или просто дробью.

Дробь устно и письменно выражается двумя числами. Первое число указывает количество долей (например, три), второе — каких долей (например, пятых).

Записывается обыкновенная дробь так: пишут число, показывающее количество долей:

Под этим числом проводят горизонтальную черту и под чертой пишут второе число, показывающее, какие это доли:

где m — нуль или натуральное число, n — натуральное число.

Таким образом, математическая запись обыкновенной дроби состоит из двух чисел, которые отделяются друг от друга горизонтальной чертой.

Пример. Изобразим единицу отрезком, который разделён на 9 долей. Отметим на нём одну, две и четыре доли:

Выразим выделенные количества долей дробями. Одна доля выражается дробью , две доли выражается дробью , четыре доли — . Каждая доля является одной девятой частью единицы:

Некоторые обыкновенные дроби имеют свои названия, которые часто используются в обиходе. Так, одна вторая доля называется иначе половиной, одна третья доля — третью, одна четвёртая доля — четвертью:

Источник

Что такое пятая часть в математике

В этой теме мы познакомимся с образованием долей, научимся их записывать, читать и сравнивать.

Доли появляются, если нам нужно разделить ЦЕЛОЕ на равные части, например, яблоко:

.

На доли можно разделить окружность:

Доля – это каждая из равных частей целого.

Название доли зависит от того, на сколько частей разделили целое.

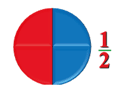
Половина

Например, яблоко разделили на две части, получилась половина яблока.

Любую долю можно записать как деление двух чисел. Мы разделили целое на две доли, каждую из долей мы можем записать в виде дроби, в которой черта обозначает знак деления.

Прочитать такую долю можно как ОДНА ВТОРАЯ.

Треть

Если целое разделили на три части, то получили ТРЕТЬ, третью часть.

Прочитать такую долю можно как ОДНА ТРЕТЬЯ.

Четверть

Если целое разделили на четыре части, получили ЧЕТВЕРТЬ, четвёртую часть.

Прочитать такую долю можно как ОДНА ЧЕТВЁРТАЯ.

Запись и чтение долей

одна пятая

одна шестая

одна восьмая

Сравнение долей

Для примера сравним две доли: одну шестую и одну третью.

Какая доля больше? Рассмотри рисунок:

Красным закрашены названные доли. Посмотри, какая доля больше? Одна третья.

Значит, одна третья часть БОЛЬШЕ, чем одна шестая часть.

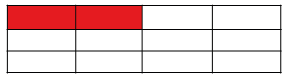
Сравним ещё две доли: одну восьмую и одну четвёртую.

Какая доля больше? Рассмотри рисунок:

Красным закрашены названные доли. Посмотри, какая доля больше? Одна четвёртая.

Значит, одна четвёртая часть БОЛЬШЕ, чем одна восьмая часть.

Вывод: Чем долей больше, тем одна её часть МЕНЬШЕ.

Поделись с друзьями в социальных сетях:

Источник

Решение простых арифметических задач, используя понятие что такое часть и целое

Сделать это очень просто.

Например: положите перед ребёнком 4 кружка красного цвета и 3 кружка синего цвета. Кружки должны быть одинакового размера и отличаться только цветом. Это обязательное условие. Предметы должны отличаться только одним признаком. Спросите, как можно назвать detkam.su все эти фигуры. Всё это кружки. Чем они отличаются? Разложи кружки на группы. Какие группы у тебя получились?

Все кружки – это целое. Целое можно разделить на части. На какие части ты разделил все кружки? (На красные кружки и синие кружки). Назови что здесь целое, а что часть-это главный вопрос упражнения.

Нужно будет научить ребёнка отвечать на вопросы:

Как, одним словом можно все эти предметы правильно назвать?

На какие части можно разделить эти предметы?

Как назовём целое? Как назовём часть? Или что здесь целое, а что часть?

Как только вы заметите, что ребёнок свободно различает и называет целое и части, начинайте при помощи тех же предметов складывать части и вычитать часть из целого. Теперь основной целью обучения является понимание, и запоминание двух основных правил, на основе которых можно решать любые задачи и уравнения на сложение и вычитание.

Следует объяснить и выучить формулу этих правил:

1) Чтобы найти целое необходимо все эти части сложить: Ц = Ч + Ч

Немного подробнее о том, как это сделать, объясню на примере с кружками красного и синего цвета. Назови что здесь целое, а что часть? Что нужно сделать, чтобы на столе остались только красные кружки? (Убрать синие кружки).

Запомни правило: Чтобы найти одну часть, нужно из целого вычесть другую(известную) часть. Что нужно сделать, чтобы на столе были все кружки? (Сложить вместе красные и синие кружки).

Запомни правило: Чтобы найти целое число, необходимо все части сложить.

Каждый раз, выполняя упражнение с разными предметами, обязательно повторяйте эти правила.

А теперь, давайте посмотрим, как применять эти правила при решении простых задач.

На веточке сидели 3 воробья и 4 синички. Сколько птичек сидело на ветке?
На столе стояло 2 чашки и столько же блюдец. Сколько посуды на столе?
Настя засушила 3 кленовых, 4 дубовых и 2 берёзовых листа. Сколько всего листьев засушила Настя?
На дереве сидели 7 птиц, 3 улетели. Сколько осталось?

Прочитай ещё раз вопрос. Что надо узнать часть или целое?

Повтори правило. Какие части нам известны и что нам о них известно? (Если надо найти целое).
Или предложите назвать известную часть и целое, если надо найти часть.

Такие арифметические задачи, как правило, затруднений не вызывают. А вот приведённые ниже задачи решить оказывается труднее, из-за того, что труднее представить условия задачи в виде картинки или фильма:

Разбирать задачу, начинаем с вопроса. Если ребёнок не совсем понял вопрос, уточните его спросив: «Ира исписала все тетради или только часть?» или «В задаче спрашивается обо всех картинках в книге или только о части картинок?» Затем действуйте по приведённому выше алгоритму.

_______________?______________
/_____воробьи_____|____синичек___\
3 4

__________9 тетр.____________________
/___исписала______|_______осталось_____\
? 6

Источник

Как решать задачи с процентами

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Основные определения

Когда мы сравниваем разные части целого, мы используем такие понятия, как половина (1/2), треть (1/3), четверть (1/4). Это удобно: отрезать половину пирога, пройти треть пути, закончить первую четверть в школе.

Чтобы сравнивать сотые доли, придумали процент (1/100): с латинского языка — «за сто».

Процент — это одна сотая часть от любого числа. Обозначается вот так: %.

Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить число на 100, как в примере выше.

А если нужно перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Например:

А вот, как перевести проценты в десятичную дробь — обратным действием:

Выразить дробь в процентах просто. Для перевода сначала превратим её в десятичную дробь, а потом используем предыдущее правило:

Типы задач на проценты

В 5, 6, 7, 8, 9 классах в задачках по математике на проценты сравнивают части одного целого, определяют долю части от целого, ищут целое по части. Давайте рассмотрим все виды задач на проценты.

Тип 1. Нахождение процента от числа

Чтобы найти процент от числа, нужно число умножить на процент.

Задача. За месяц на заводе изготовили 500 стульев. 20% изготовленных стульев не прошли контроль качества. Сколько стульев не прошло контроль качества?

Как решаем: нужно найти 20% от общего количества изготовленных стульев (500).

Из общего количества изготовленных стульев контроль не прошли 100 штук.

Тип 2. Нахождение числа по его проценту

Чтобы найти число по его проценту, нужно его известную часть разделить на то, сколько процентов она составляет от числа.

Задачи по поиску процента по числу и числа по его проценту очень похожи. Чтобы не перепутать — внимательно читаем условия, иначе зайдем в тупик или решим неправильно. Если в задании есть слова «который», «что составляет» и «который составляет» — перед нами задача по нахождению числа по его проценту.

Задача. Школьник решил 38 задач из учебника. Что составляет 16% числа всех задач в книге. Сколько всего задач собрано в этом учебнике?

Как решаем: мы не знаем, сколько всего задач в учебнике. Но нам известно, что 38 задач составляют 16% от общего количества. Запишем 16% в виде дроби: 0,16. Далее известную нам часть целого разделим на ту долю, которую она составляет от всего целого.

38/0,16 = 38 * 100/16 = 237,5

Значит 237 задачи включили в этот сборник.

Тип 3. Нахождение процентного отношения двух чисел

Чтобы найти, сколько процентов одно число составляет от другого, нужно ту часть, о которой спрашивается, разделить на общее количество и умножить на 100%.

Задача. В классе учится 25 человек. 10 из них — девочки. Сколько процентов девочек в классе?

Как решаем: возьмем алгоритм из правила выше:

10/25 * 100% = 2/5 * 100% = 2 * 100/5 = 40%

В классе учится 10 девочек — это 40%.

Тип 4. Увеличение числа на процент

Чтобы увеличить число на некоторое количество процентов, нужно найти число, которое выражает нужное количество процентов от данного числа, и сложить его с данным числом.

Формула расчета процента от числа выглядит так:

где a — число, которое нужно найти,

b — первоначальное значение,

c — проценты.

Задача. В прошлом месяце стикер-пак стоил 110 рублей. А в этом месяце на 12% больше. Сколько стоит стикер-пак?

Как решаем: подставим в формулу данные из условий задачи.

110 * (1 + 12/100) = 110 * 1,12 = 123,2.

Стоимость стикер-пака в этом месяце — 123 рубля 20 копеек.

Тип 5. Уменьшение числа на процент

Чтобы уменьшить число на несколько процентов, нужно найти число, которое выражает нужное количество процентов данного числа, и вычесть его от данного числа.

Формула расчета выглядит так:

где a — число, которое нужно найти,

b — первоначальное значение,

c — проценты.

Задача. В прошлом году школу закончили 100 ребят. А в это году выпускников на 25 меньше. Сколько выпускников в этом году?

Как решаем: подставим в формулу данные из условий задачи.

75 выпускников закончат школу в этом году.

Тип 6. Задачи на простые проценты

Простые проценты — метод расчета процентов, при котором начисления происходят на первоначальную сумму вклада или долга.

Формула расчета выглядит так:

где a — исходная сумма,

S — сумма, которая наращивается,

x — процентная ставка,

y — количество периодов начисления процента.

Задача. Родители взяли в банке кредит 5000 рублей, чтобы купить тебе что-то классное. Кредит на год под 15% ежемесячно. Сколько денег они внесут через год?

Как решаем: подставим в формулу данные из условий задачи.

5000 * (1 + 12 * 15/100) = 14000

Родители через год внесут в банк 14000 рублей.

Тип 7. Задачи на сложные проценты

Сложные проценты — это метод расчета процентов, когда проценты прибыли прибавляют к сумме на остатке каждый месяц. В следующий раз проценты начисляют на эту новую сумму.

Формула расчета выглядит так:

где S — наращиваемая сумма,

a — исходная,

x — процентная ставка,

y — количество периодов начисления процента.

Задача. Папа взял в банке кредит 25000 рублей на 3 месяца под 15%. Нам нужно узнать, сколько денег придется заплатить банку по истечении срока кредита.

Как решаем: просто подставим в формулу данные из условий задачи:

25000 * (1 + 15/100)3 = 38021,875 — искомая сумма.

Курсы по математике для учеников с 1 по 11 классы. Вводный урок — бесплатно!

Способы нахождения процента

Универсальная формула для решения задач на проценты:

Чтобы применить алгоритм, нужно прочитать задачу, отметить, какие два числа нам известны и найти третье.

Есть еще четыре способа поиска процентов. Рассмотрим каждый из них.

Деление числа на 100

При делении на 100 получается 1% от этого числа. Это правило можно использовать по-разному. Например, чтобы узнать процент от суммы, нужно умножить их на размер 1%. А чтобы перевести известное значение, следует разделить его на размер 1%. Этот метод отлично помогает в вопросе, как перевести целое число в проценты.

Представьте, что вы пришли в магазин за шоколадом. Обычно он стоит 250 рублей, но сегодня скидка 15%. Если у вас есть дисконтная карта магазина, шоколад обойдется вам в 225 рублей. Чем будет выгоднее воспользоваться: скидкой или картой?

Ответ: выгоднее воспользоваться скидкой 15%.

Составление пропорции

Пропорция — определенное соотношение частей между собой.

С помощью метода пропорции можно рассчитать любые %. Выглядит это так:

Читается: a относится к b так, как с относится к d. Также важно помнить, что произведение крайних членов равно произведению средних. Чтобы узнать неизвестное из этого равенства, нужно решить простейшее уравнение.

Рассмотрим пример. На сколько выгодно покупать спортивную футболку за 1390 рублей при условии, что в магазине в честь дня всех влюбленных действует скидка 14%?

Ответ: купить спортивную футболку выгоднее на 194,6 рубля.

Соотношения чисел

Есть случаи, при которых можно использовать простые дроби.

Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?

Ответ: средств хватит, так как пиджак стоит 6375 рублей.

Задачи на проценты с решением

Как мы уже убедились, решать задачи на проценты совсем несложно. Для закрепления материала рассмотрим реальные примеры на проценты из учебников и несколько заданий для подготовки к ЕГЭ.

Задача 1. Организм взрослого человека на 70% состоит из воды. Какова масса воды в теле человека, который весит 76 кг?

76 : 100 = 0,76 — 1% от массы человека

Ответ: масса воды 53,2 кг

Задача 2. Цена товара понизилась на 40%, затем еще на 25%. На сколько процентов понизилась цена товара по сравнению с первоначальной ценой?

Обозначим первоначальную цену товара через х. После первого понижения цена станет равной.

Второе понижение цены составляет 25% от новой цены 0,6х, поэтому после второго понижения получим:

После двух понижений изменение цены составит:

Так как величина 0,55x составляет 55% от величины x, то цена товара понизилась на 55%.

Задача 3. Четыре пары брюк дешевле одного пальто на 8%. На сколько процентов пять пар брюк стоят дороже, чем одно пальто?

По условиям задачи стоимость четырех пар брюк — это 92% от стоимости пальто

Получается, что стоимость одной пары брюк — это 23% стоимости пальто.

Теперь умножим стоимость одной пары брюк на пять и узнаем, что пять пар брюк обойдутся в 115% стоимости пальто.

Ответ: пять пар брюк на 15% дороже, чем одно пальто.

Задача 4. Семья состоит из трех человек: муж, жена и дочь-студентка. Если зарплата мужа вырастет в два раза, общий доход семьи возрастет на 67%. Если дочери в три раза урежут стипендию, общий доход этой семьи уменьшится на 4%. Вычислить, какой процент в общий доход семьи приносит заработок жены.

По условиям задачи общий доход семьи напрямую зависит от доходов мужа. Благодаря увеличению зарплаты общий доход семьи вырастет на 67%. Значит, зарплата мужа составляет как раз 67% от общего дохода.

Если стипендия дочери уменьшится в три раза (т.е. на 1/3), останется 2/3 — это и есть 4%, на которые уменьшился бы семейных доход.

Можно составить простую пропорцию и выяснить, что раз 2/3 стипендии — это 4% дохода, то вся стипендия — это 6%.

А теперь отнимем от всего дохода вклад мужа и дочери и узнаем, какой процент составляет заработок жены в общем доходе семьи: 100 – 67 – 6 = 27.

Ответ: заработок жены составляет 27%.

Задача 5. В свежих абрикосах 90% влаги, а в сухофрукте кураге только 5%. Сколько килограммов абрикосов нужно, чтобы получить 20 килограммов кураги?

Исходя из условия, в абрикосах 10% питательного вещества, а в кураге в концентрированном виде — 95%.

Поэтому в 20 килограммах кураги 20 * 0,95 = 19 кг питательного вещества.

На вопрос задачи мы ответим, если разделим одинаковое количество питательного вещества, которое содержится в разных объемах свежих абрикосов и кураги, на его процентное содержание в абрикосах.

Ответ: 190 кг свежих абрикосов потребуется для изготовления 20 кг кураги.

Источник

Обыкновенные дроби

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Доля целого

Доля — это каждая равная часть, из суммы которых состоит целый предмет.

Для примера возьмем два мандарина. Когда мы их почистим, то получим в каждом мандарине разное количество долек или долей. В одном может быть 6, а в другом — целых 9. Размеры долей у каждого мандарина тоже разные.

У каждой доли есть свое название: оно зависит от количества долей в конкретном предмете. Если в мандарите шесть долей — каждая из них будет определяться, как одна шестая от целого.

Понятие доли можно применить не только к предметам, но и величинам. Так, например, картина занимает четверть стены — при этом ее ширина треть метра.

Чтобы быстрее запомнить соотношения частей и целого, можно использовать наглядную табличку:

Понятие дроби

Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:

Виды дробей:

Какие еще бывают дроби:

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.

Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3\5.

Выделение целой части из неправильной дроби — это запись неправильной дроби в виде суммы натурального числа и правильной дроби. Например, 11/5 = 2 + 1/5.

Как устроена обыкновенная дробь

Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.

Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.

Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.

Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим.

Черта между числителем и знаменателем — символ деления.

Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.

Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.

Как устроена десятичная дробь

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Свойства дробей

Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:

где a, b, k — натуральные числа.

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:

У нас есть отличные курсы по математике для учеников с 1 по 11 классы, записывайтесь!

Действия с дробями

С дробями можно выполнять те же действия, что и с обычными числами: складывать, вычитать, умножать и делить. А еще дроби можно сокращать и сравнивать между собой. Давайте попробуем.

Сравнение дробей

Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.

Сравним 1/5 и 4/5. Как рассуждаем:

Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. А после приведения дробей к общему знаменателю, можно применить правило сравнения дробей с одинаковыми знаменателями.

Пример. Сравнить 2/7 и 1/14.

Важно запомнить: любая неправильная дробь больше любой правильной. Потому что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.

Чтобы сравнить дроби с разными числителями и знаменателями, нужно:

Чтобы привести дроби к наименьшему общему знаменателю, нужно:

Сокращение дробей

Сокращение дроби — это деление числителя и знаменателя дроби на одно и то же натуральное число. Сократить дробь значит сделать ее короче и проще для восприятия. Например, дробь 1/3 выглядит намного проще и красивее, чем 27/81.

Сокращение дроби выглядит так: зачеркивают числитель и знаменатель, а рядом записывают результаты деления числителя и знаменателя на одно и то же число.

В этом примере делим обе части дроби на двойку.

Можно никуда не спешить и сокращать дроби последовательно, в несколько действий.

Сложение и вычитание дробей

При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.

Не забудьте проверить, можно ли сократить дробь и выделить целую часть.

При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).

Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.

НОК (15, 18) = 3 * 2 * 3 * 5 = 90

Полученные числа запишем справа сверху над числителем.

Ход решения одной строкой:

Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:

Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.

Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.

Умножение и деление дробей

Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:

Не забываем про сокращение. Это может облегчить вычисления.

Чтобы умножить два смешанных числа, надо:

Чтобы разделить дробь на дробь нужно выполнить следующую последовательность действий:

Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.

Числа, произведение которых равно 1, называют взаимно обратными.

Как делить дроби с разными знаменателями? На самом деле одинаковые или разные знаменатели у дробей — неважно, потому что все дроби делятся по правилу, описанному выше.

Для деления смешанных чисел необходимо:

Источник