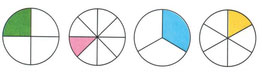
Что такое пятая часть
Что такое пятая часть
В этой теме мы познакомимся с образованием долей, научимся их записывать, читать и сравнивать.
Доли появляются, если нам нужно разделить ЦЕЛОЕ на равные части, например, яблоко:

На доли можно разделить окружность:
Доля – это каждая из равных частей целого.
Название доли зависит от того, на сколько частей разделили целое.
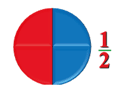
Половина
Например, яблоко разделили на две части, получилась половина яблока.
Любую долю можно записать как деление двух чисел. Мы разделили целое на две доли, каждую из долей мы можем записать в виде дроби, в которой черта обозначает знак деления.
Прочитать такую долю можно как ОДНА ВТОРАЯ.
Треть
Если целое разделили на три части, то получили ТРЕТЬ, третью часть.
Прочитать такую долю можно как ОДНА ТРЕТЬЯ.
Четверть
Если целое разделили на четыре части, получили ЧЕТВЕРТЬ, четвёртую часть.
Прочитать такую долю можно как ОДНА ЧЕТВЁРТАЯ.
Запись и чтение долей



Сравнение долей
Для примера сравним две доли: одну шестую и одну третью.
Какая доля больше? Рассмотри рисунок:
Красным закрашены названные доли. Посмотри, какая доля больше? Одна третья.
Значит, одна третья часть БОЛЬШЕ, чем одна шестая часть.
Сравним ещё две доли: одну восьмую и одну четвёртую.
Какая доля больше? Рассмотри рисунок:
Красным закрашены названные доли. Посмотри, какая доля больше? Одна четвёртая.
Значит, одна четвёртая часть БОЛЬШЕ, чем одна восьмая часть.
Вывод: Чем долей больше, тем одна её часть МЕНЬШЕ.
Поделись с друзьями в социальных сетях:
Что такое круг пятых и как его можно использовать в написании песен?

Что такое пятая часть?
Интервал пятерки равен семи полушагам. Это понятие может показаться немного неинтуитивным; вы можете подумать, что пятая часть должна быть равна пяти полушагам, верно? Давайте посмотрим немного ближе.
Несмотря на то, что от C до G семь полушагов, G находится всего в пяти буквах от C (C, D, E, F, G). Все, что находится на расстоянии 5 букв друг от друга, обозначается пятой долей. То же самое относится и к другим интервалам, но мы оставим эту кроличью нору для другого раза.
Использование круга в написании песен
Прежде чем углубиться в теорию, вы, возможно, зададитесь вопросом, как я могу использовать эти паттерны в написании песен? Не можем ли мы просто перейти к самому интересному?
Использование пятых для построения круга
Теперь, когда вы понимаете, что пятая часть равна семи половинным ступеням, вы можете использовать это знание для построения круга пятых.
Для начала нарисуйте круг и поставьте 12 равномерно расположенных точек по внешней стороне, как цифры на часах. Нарисуйте букву «С» в верхней части круга следующим образом:
Двигаясь по кругу по часовой стрелке, следующая нота будет пятой вверх от С. Отсчитайте семь полушагов вверх от С, и вы достигнете G. Отметьте G в положении «один час» на круге следующим образом:
Ключевые подписи и энгармонические эквиваленты
Эта схема продолжается до тех пор, пока мы не достигнем мажорной гаммы C♯, в которой семь диезов. На этом этапе все ноты в мажорной гамме диезные, поэтому, если мы хотим продолжить, нам нужно добавить двойные диезы. Двойные диезы довольно сложны для быстрого осмысления, поэтому большинство людей переходят к бемольным клавишам, используя концепцию энгармонических эквивалентов.
Использование энгармонических эквивалентов для завершения круга
Вернитесь на несколько шагов назад к ноте B на круге. Можете ли вы вспомнить энгармонический эквивалент ноты B? Если вы играете на клавишном инструменте, посмотрите на одну клавишу вправо от B. В противном случае переместитесь на одну ноту вправо в музыкальном алфавите, а затем добавьте бемоль.
C♭ является энгармоническим эквивалентом B. Отметьте C♭ на внутренней стороне круга следующим образом:
Поздравляем! Вы успешно построили круг пятых!
Некоторые основные узоры на окружности
Ранее мы узнали, что мажорный ключ, расположенный в верхней части круга, не имеет ни диезов, ни бемолей и что мажорный ключ C♯ имеет семь диезов. Отсюда следует, что мажорный лад C♭ будет иметь семь бемолей. Если мы соединим эти три точки на окружности, то получим треугольник, который выглядит следующим образом:
Продолжаем, на чем остановились
Начиная с аккорда F, сделайте один шаг против часовой стрелки до B♭. Затем перейдите на A♭ и сделайте один шаг против часовой стрелки до D♭. Посмотрите, можете ли вы проследить этот узор на вашем круге, он должен быть довольно простым. Теперь давайте поработаем с ним.
Вы можете использовать этот подход практически для любой песни. Вы обнаружите, что большинство популярных аккордовых прогрессий хорошо ложатся на круг пятых.
Вырастите свой собственный
Вы также можете использовать круг как инструмент для построения собственных аккордовых прогрессий. Например, начните с соль минора. Как он будет звучать, если вы перейдете от соль минора на шаг по часовой стрелке к ре мажору? А как насчет ре минора? А что если перейти по кругу к фа мажору, за которым последует фа минор? Затем перейти по часовой стрелке к до и, наконец, вернуться к соль минору?
Заключение
Круг пятых подобен музыкальному цветовому кругу. Это способ организации всех 12 тонов таким образом, чтобы каждый лад находился на равном расстоянии друг от друга. Эта структура также содержит прогрессию ключевых подписей, что может быть полезно при чтении нотной записи или сочинении мелодий. Обучение использованию пятых ладов принесет много пользы при написании песен и поможет углубить понимание музыки при каждом прослушивании.
Как решать задачи с процентами
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные определения
Когда мы сравниваем разные части целого, мы используем такие понятия, как половина (1/2), треть (1/3), четверть (1/4). Это удобно: отрезать половину пирога, пройти треть пути, закончить первую четверть в школе.
Чтобы сравнивать сотые доли, придумали процент (1/100): с латинского языка — «за сто».
Процент — это одна сотая часть от любого числа. Обозначается вот так: %.
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить число на 100, как в примере выше.
А если нужно перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Например:
А вот, как перевести проценты в десятичную дробь — обратным действием:
Выразить дробь в процентах просто. Для перевода сначала превратим её в десятичную дробь, а потом используем предыдущее правило:
Типы задач на проценты
В 5, 6, 7, 8, 9 классах в задачках по математике на проценты сравнивают части одного целого, определяют долю части от целого, ищут целое по части. Давайте рассмотрим все виды задач на проценты.
Тип 1. Нахождение процента от числа
Чтобы найти процент от числа, нужно число умножить на процент.
Задача. За месяц на заводе изготовили 500 стульев. 20% изготовленных стульев не прошли контроль качества. Сколько стульев не прошло контроль качества?
Как решаем: нужно найти 20% от общего количества изготовленных стульев (500).
Из общего количества изготовленных стульев контроль не прошли 100 штук.
Тип 2. Нахождение числа по его проценту
Чтобы найти число по его проценту, нужно его известную часть разделить на то, сколько процентов она составляет от числа.
Задачи по поиску процента по числу и числа по его проценту очень похожи. Чтобы не перепутать — внимательно читаем условия, иначе зайдем в тупик или решим неправильно. Если в задании есть слова «который», «что составляет» и «который составляет» — перед нами задача по нахождению числа по его проценту.
Задача. Школьник решил 38 задач из учебника. Что составляет 16% числа всех задач в книге. Сколько всего задач собрано в этом учебнике?
Как решаем: мы не знаем, сколько всего задач в учебнике. Но нам известно, что 38 задач составляют 16% от общего количества. Запишем 16% в виде дроби: 0,16. Далее известную нам часть целого разделим на ту долю, которую она составляет от всего целого.
38/0,16 = 38 * 100/16 = 237,5
Значит 237 задачи включили в этот сборник.
Тип 3. Нахождение процентного отношения двух чисел
Чтобы найти, сколько процентов одно число составляет от другого, нужно ту часть, о которой спрашивается, разделить на общее количество и умножить на 100%.
Задача. В классе учится 25 человек. 10 из них — девочки. Сколько процентов девочек в классе?
Как решаем: возьмем алгоритм из правила выше:
10/25 * 100% = 2/5 * 100% = 2 * 100/5 = 40%
В классе учится 10 девочек — это 40%.
Тип 4. Увеличение числа на процент
Чтобы увеличить число на некоторое количество процентов, нужно найти число, которое выражает нужное количество процентов от данного числа, и сложить его с данным числом.
Формула расчета процента от числа выглядит так:
где a — число, которое нужно найти,
b — первоначальное значение,
c — проценты.
Задача. В прошлом месяце стикер-пак стоил 110 рублей. А в этом месяце на 12% больше. Сколько стоит стикер-пак?
Как решаем: подставим в формулу данные из условий задачи.
110 * (1 + 12/100) = 110 * 1,12 = 123,2.
Стоимость стикер-пака в этом месяце — 123 рубля 20 копеек.
Тип 5. Уменьшение числа на процент
Чтобы уменьшить число на несколько процентов, нужно найти число, которое выражает нужное количество процентов данного числа, и вычесть его от данного числа.
Формула расчета выглядит так:
где a — число, которое нужно найти,
b — первоначальное значение,
c — проценты.
Задача. В прошлом году школу закончили 100 ребят. А в это году выпускников на 25 меньше. Сколько выпускников в этом году?
Как решаем: подставим в формулу данные из условий задачи.
75 выпускников закончат школу в этом году.
Тип 6. Задачи на простые проценты
Простые проценты — метод расчета процентов, при котором начисления происходят на первоначальную сумму вклада или долга.
Формула расчета выглядит так:
где a — исходная сумма,
S — сумма, которая наращивается,
x — процентная ставка,
y — количество периодов начисления процента.
Задача. Родители взяли в банке кредит 5000 рублей, чтобы купить тебе что-то классное. Кредит на год под 15% ежемесячно. Сколько денег они внесут через год?
Как решаем: подставим в формулу данные из условий задачи.
5000 * (1 + 12 * 15/100) = 14000
Родители через год внесут в банк 14000 рублей.
Тип 7. Задачи на сложные проценты
Сложные проценты — это метод расчета процентов, когда проценты прибыли прибавляют к сумме на остатке каждый месяц. В следующий раз проценты начисляют на эту новую сумму.
Формула расчета выглядит так:
где S — наращиваемая сумма,
a — исходная,
x — процентная ставка,
y — количество периодов начисления процента.
Задача. Папа взял в банке кредит 25000 рублей на 3 месяца под 15%. Нам нужно узнать, сколько денег придется заплатить банку по истечении срока кредита.
Как решаем: просто подставим в формулу данные из условий задачи:
25000 * (1 + 15/100)3 = 38021,875 — искомая сумма.
Курсы по математике для учеников с 1 по 11 классы. Вводный урок — бесплатно!
Способы нахождения процента
Универсальная формула для решения задач на проценты:
| A * b = C, где A — исходное число, b — проценты, переведенные в десятичную дробь, C — новое число. |
Чтобы применить алгоритм, нужно прочитать задачу, отметить, какие два числа нам известны и найти третье.
Есть еще четыре способа поиска процентов. Рассмотрим каждый из них.
Деление числа на 100
При делении на 100 получается 1% от этого числа. Это правило можно использовать по-разному. Например, чтобы узнать процент от суммы, нужно умножить их на размер 1%. А чтобы перевести известное значение, следует разделить его на размер 1%. Этот метод отлично помогает в вопросе, как перевести целое число в проценты.
Представьте, что вы пришли в магазин за шоколадом. Обычно он стоит 250 рублей, но сегодня скидка 15%. Если у вас есть дисконтная карта магазина, шоколад обойдется вам в 225 рублей. Чем будет выгоднее воспользоваться: скидкой или картой?
Ответ: выгоднее воспользоваться скидкой 15%.
Составление пропорции
Пропорция — определенное соотношение частей между собой.
С помощью метода пропорции можно рассчитать любые %. Выглядит это так:
Читается: a относится к b так, как с относится к d. Также важно помнить, что произведение крайних членов равно произведению средних. Чтобы узнать неизвестное из этого равенства, нужно решить простейшее уравнение.
Рассмотрим пример. На сколько выгодно покупать спортивную футболку за 1390 рублей при условии, что в магазине в честь дня всех влюбленных действует скидка 14%?
Ответ: купить спортивную футболку выгоднее на 194,6 рубля.
Соотношения чисел
Есть случаи, при которых можно использовать простые дроби.
Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?
Ответ: средств хватит, так как пиджак стоит 6375 рублей.
Задачи на проценты с решением
Как мы уже убедились, решать задачи на проценты совсем несложно. Для закрепления материала рассмотрим реальные примеры на проценты из учебников и несколько заданий для подготовки к ЕГЭ.
Задача 1. Организм взрослого человека на 70% состоит из воды. Какова масса воды в теле человека, который весит 76 кг?
76 : 100 = 0,76 — 1% от массы человека
Ответ: масса воды 53,2 кг
Задача 2. Цена товара понизилась на 40%, затем еще на 25%. На сколько процентов понизилась цена товара по сравнению с первоначальной ценой?
Обозначим первоначальную цену товара через х. После первого понижения цена станет равной.
Второе понижение цены составляет 25% от новой цены 0,6х, поэтому после второго понижения получим:
После двух понижений изменение цены составит:
Так как величина 0,55x составляет 55% от величины x, то цена товара понизилась на 55%.
Задача 3. Четыре пары брюк дешевле одного пальто на 8%. На сколько процентов пять пар брюк стоят дороже, чем одно пальто?
По условиям задачи стоимость четырех пар брюк — это 92% от стоимости пальто
Получается, что стоимость одной пары брюк — это 23% стоимости пальто.
Теперь умножим стоимость одной пары брюк на пять и узнаем, что пять пар брюк обойдутся в 115% стоимости пальто.
Ответ: пять пар брюк на 15% дороже, чем одно пальто.
Задача 4. Семья состоит из трех человек: муж, жена и дочь-студентка. Если зарплата мужа вырастет в два раза, общий доход семьи возрастет на 67%. Если дочери в три раза урежут стипендию, общий доход этой семьи уменьшится на 4%. Вычислить, какой процент в общий доход семьи приносит заработок жены.
По условиям задачи общий доход семьи напрямую зависит от доходов мужа. Благодаря увеличению зарплаты общий доход семьи вырастет на 67%. Значит, зарплата мужа составляет как раз 67% от общего дохода.
Если стипендия дочери уменьшится в три раза (т.е. на 1/3), останется 2/3 — это и есть 4%, на которые уменьшился бы семейных доход.
Можно составить простую пропорцию и выяснить, что раз 2/3 стипендии — это 4% дохода, то вся стипендия — это 6%.
А теперь отнимем от всего дохода вклад мужа и дочери и узнаем, какой процент составляет заработок жены в общем доходе семьи: 100 – 67 – 6 = 27.
Ответ: заработок жены составляет 27%.
Задача 5. В свежих абрикосах 90% влаги, а в сухофрукте кураге только 5%. Сколько килограммов абрикосов нужно, чтобы получить 20 килограммов кураги?
Исходя из условия, в абрикосах 10% питательного вещества, а в кураге в концентрированном виде — 95%.
Поэтому в 20 килограммах кураги 20 * 0,95 = 19 кг питательного вещества.
На вопрос задачи мы ответим, если разделим одинаковое количество питательного вещества, которое содержится в разных объемах свежих абрикосов и кураги, на его процентное содержание в абрикосах.
Ответ: 190 кг свежих абрикосов потребуется для изготовления 20 кг кураги.
Десятичные дроби
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
Обучение на курсах по математике — отличный способ закрепить полученные знания на практике и подтянуть сложные темы.
Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.
Пример 2. Перевести 37/1000 в десятичную дробь.
Ответ: 37/1000 = 0,037.
Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
| и т.д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Преобразование десятичных дробей
Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!
Как перевести десятичную дробь в проценты
Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.
А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:
Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.
2/5 = 0,4
0,4 · 100% = 40%
8/25 = 0,32
0,32 · 100% = 32%
Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:
Преобразование десятичных дробей
Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.
Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).
Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!
Пример 1. Перевести 5,4 в смешанное число.
Пример 2. Перевести 4,005 в смешанное число.
Ответ: 4,005 = 4 1/200.
Пример 3. Перевести 5,60 в смешанное число.
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
Действия с десятичными дробями
С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.
Как разделить десятичную дробь на натуральное число
Пример 2. Разделить 183,06 на 45.
Ответ: 183,06 : 45 = 4,068.
Как разделить десятичную дробь на обыкновенную
Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.
Пример 1. Разделить 0,25 на 3/4.
Пример 2. Разделить 2,55 на 1 1/3.
Ответ: 2,55 : 1 1/3 = 1 73/80.
Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Пример 1. Умножить 2/5 на 0,8.
Пример 2. Умножить 0,28 на 6 1/4.
Ответ: 0,28 ∗ 6 1/4 = 0,8.