Что такое спектр в музыке
Спектр звука
Смотреть что такое «Спектр звука» в других словарях:
СПЕКТР ЗВУКА — выражает частотный состав звука и получается врезультате звука анализа. С. з. представляют обычно на координатнойплоскости, где по оси абсцисс отложена частота f, по оси ординат амплитуда А или интенсивность I гармонической составляющейзвука.… … Физическая энциклопедия
спектр звука — garso spektras statusas T sritis fizika atitikmenys: angl. audible spectrum; sound spectrum vok. Klangspektrum, n; Schallspektrum, n rus. звуковой спектр, m; спектр звука, m pranc. spectre acoustique, m; spectre du son, m; spectre sonore, m … Fizikos terminų žodynas
спектр звука — garso spektras statusas T sritis Standartizacija ir metrologija apibrėžtis Sudėtinio (kelių tonų) garso skirtingų amplitudžių ir dažnių harmoninių virpesių visuma. atitikmenys: angl. acoustic spectrum; sound spectrum vok. akustisches Spektrum, n; … Penkiakalbis aiškinamasis metrologijos terminų žodynas
СПЕКТР ЗВУКА — (от лат. spectrum видимое, видение. ) объективная характеристика звука сложного состава, отражающая его внутреннюю физическую структуру (в отличие от внешней структуры, отражаемой формой колебаний или осциллограммой). С. з. графически… … Энциклопедический словарь по психологии и педагогике
Спектр звука — совокупность простых гармонических волн, на которые можно разложить сложную звуковую волну. Получить С. какого либо звука значит получить совокупность значений амплитуд всех частотных составляющих, образующих данный звук. Такой С. называется… … Педагогическое речеведение
Спектр звука (света) — спектр звука (света): интенсивность или уровень звукового давления применительно к звуку (свету), представляющие собой функцию частоты или длины волны. Источник: ГОСТ Р 51340 99. Государственный стандарт Российской Федерации. Безопасность машин … Официальная терминология
спектр звука (света) — спектр звука (света): Интенсивность или уровень звукового давления применительно к звуку (свету), представляющие собой функцию частоты или длины волны; Источник … Словарь-справочник терминов нормативно-технической документации
акустический спектр звука — acoustical spectrum совокупность синусоидальных составляющих сложного звука, заданных с помощью амплитуд и частот этих составляющих … Русский индекс к Англо-русскому словарь по музыкальной терминологии
ЗВУКА АНАЛИЗ — разложение сложного звук. процесса на ряд простых колебаний. Применяются два вида З. а.: частотный и временной. При частотном З. а. звук. сигнал представляется суммой гармонич. составляющих, характеризующихся частотой, фазой и амплитудой.… … Физическая энциклопедия
Спектр (в физике) — Спектр (от лат. spectrum ≈ представление, образ) в физике, совокупность различных значений, которые может принимать данная физическая величина. С. могут быть непрерывными и дискретными (прерывными). Наиболее часто понятие С. применяется к… … Большая советская энциклопедия
Что такое спектр и от чего зависит уровень шумовой полки? FAQ для «чайников»
Именно для этой категории пользователей и сделан краткий FAQ на простых примерах о спектрах.
Прежде всего, спектр, это не набор синусов в чистом виде. Это набор частотных полос равной ширины с определенным уровнем мощности. Эти полосы частот называются бинами.
Количество и ширина бинов зависит от величины спектрального окна FFT Size. Если величина окна равна 32-м семплам, то мы получим 16 бинов (количество бинов всегда в два раза меньше величины окна). Ширина бинов будет зависеть от частоты дискретизации и для 44,1 кГц это будет 1378 Гц. Первый бин будет представлять частотный диапазон от 0 до 1378, второй от 1378 до 2756 и т.д.
Когда берется окно с малым количеством семплов, то у нас определенно частотные полосы, которые нельзя сопоставить с конкретной частотой. Бин с диапазоном от 0 до 1378 Гц не являет ни частотой 500 Гц, ни 1 кГц, а является суммой мощностей частот с 0 до 1378 Гц.
Для окна в 65536 семплов будет 32768 бина с шириной в 0,67 Гц. На графике на 1 пиксель будет приходится по сотне бинов, а конечная амплитуда будет взята по максимально высокому бину. Для такого окна для частоты в 500 Гц есть бин с диапазоном от 499,974 до 500,646 Гц и формально идеологическая разница между бином, как частотный диапазоном и просто частотой исчезает.
Величина окна в семплах – это сколько взяли последовательных координат из звуковой волны. Чем больше величина окна в семплах, тем более длинный участок звуковой волны анализируется.
По этой причине, не зная исходных данных для FFT Size, невозможно по виду спектра определить конечную суммарную мощность шума.
Более того, так как уровень шума все равно визуально определить нельзя, то его «давят» всеми возможными способами, начиная от использования весовых окон и заканчивая различным усреднением спектров.
Основной задачей спектров является выявление периодических сигналов. И чем больше величина FFT Size, тем ниже шумовая полка и отчетливее видно основные гармоники. И разумеется, чем больше величина FFT Size, тем точнее мы можем определить частоту каждой гармоники.
Независимо от величины FFT Size, бины, содержащие гармонические сигналы, постоянны по своей мощности, в то время как содержащие шум при последующем делении уменьшаются по амплитуде. При делении же бина с гармоническим сигналом, тот бин, в который попадает гармонический сигнал принимает его мощность, а остальные получаются с мощностью шумовой полки.
Так как для большого окна надо использовать сигнал большой продолжительности, то величину FFT Size ставят разную в зависимости от ситуации. Где-то достаточно малого окна, что бы бегло оценить общий характер спектра, где-то для работы в real-time доступны лишь небольшие окна. Где-то нет смысла получать спектр «под микроскопом». А где-то спектр строит «прибор», который физически ограничен по максимальному значению. FFT анализ требует не малых ресурсов и при увеличении FFT Size нагрузка на процессор и величину используемой оперативной памяти растет по экспоненте.
Именно по этой причине графики на одно устройство, сделанные в разном софте совпадают по уровню основных гармоник, но существенно отличаются по уровню шумовой полки.
Почему еще стараются подавить шум? Спектр не является строго одинаковым в любой момент времени. Гармонические сигналы постоянной амплитуды с течением времени меняются крайне незначительно, а вот шум меняется постоянно. Если сделать усреднение по нескольким спектрам, то мы можем визуально «отфильтровать» часть шума и отчетливее увидеть основные гармоники.
В отчетах Reference Audio Analyzer проводится анализ в следующих типах разрешения спектра.
Для анализа на длительных сигналах используется FFT Size 262144 семпла с 18 кратным усреднением. Для этого требуется тестовый участок длительностью в минуту.
Для тестов зависимости искажений от амплитуды используются более короткие тестовые участки с FFT Size 65536 с двукратным усреднением. Для этого требуется участок в 3 сек. Конечно, хотелось бы все графики получать с максимально большим FFT Size, но тогда тест будет требовать уже не один час а целый месяц и количество протестированных устройств пропорционально сократится.
Для теста мультитонов используется FFT Size 2097152 семпла для минутного участка без усреднения. Такой вариант не самый эффективный по подавлению шума, но позволяет получить максимально возможную разборчивость в низкочастотной области.
О звуках, спектрах и обманутых ожиданиях
(c) Илья Мамонтов, 2021
Согласно общепринятой теории фазовые соотношения в спектре звука не важны для восприятия тембра. Как выясняется, это справедливо лишь отчасти (для частот выше 200 Гц). Для звуков низкой частоты (менее сотни Гц) начинает работать другой механизм, в чем и предлагаю убедиться.
Вначале небольшая предыстория.
Мне как-то потребовался периодический звуковой сигнал с достаточно широким спектром (много гармоник). Таким свойством обладает последовательность очень коротких импульсов, вот только их энергия заключена в коротких интервалах времени. При сохранении средней мощности сигнала это приводит к росту пиковой амплитуды. А диапазон что в аналоге, что в цифре – он ограничен. Лучшими амплитудными свойствами обладает двуполярный импульс, но у меня возник вопрос – а можно ли создать такой широкополосный периодический сигнал, чтобы его энергия была равномерно «размазана» по всему периоду? И как он будет выглядеть, если его спектр ограничить некоторой максимальной частотой (для реализации в цифре?).
Интуиция подсказывала варьировать начальные фазы гармоник, но готового решения я нигде не нашел. Тогда начались эксперименты, во время которых выяснилось, что общепринятое представление об отсутствии влияния фазы на восприятие тембра справедливо лишь отчасти. Для высоких звуков это выполняется на 100%, но перестает работать для звуков низкой частоты. Сей факт указывает на то, что в низкочастотной области начинает действовать другой механизм, отличный от спектрального анализа, вроде бы как производимого органом слуха. Вопрос требует дальнейшего изучения (с возможным пересмотром физиологии), здесь же просто демонстрируется этот факт.
Итак, сгенерируем тестовый сигнал с ограниченным спектром – основной тон и первые 19 гармоник (со 2-й по 20-ую), все – с одинаковыми амплитудами. Выбор такого сигнала обусловлен возможностью свободно менять его частоту и не заморачиваться при этом с критерием Котельникова-Найквиста (невыполнение которого приводит к появлению побочных частот-призраков) при экспериментах на компьютере. При стандартной частоте дискретизации 44100 Гц это даст максимальную позволенную частоту основного тона 1100 Гц, что вполне достаточно для покрытия музыкального диапазона (более высокие ноты хоть и употребляются на практике, но воспринимаются больше как писк). Для тестирования выберем три частоты, отстоящие друг от друга достаточно далеко – 40, 200 и 800 Гц.
Если суммировать косинусоиды, то получим форму сигнала, приближающуюся к дельта-функции (короткий высокий импульс):
Если суммировать синусоиды (это те же косинусоиды, только сдвинутые на угол пи/2), получим последовательность двуполярных импульсов:
Пока все идет в соответствии с теорией, и даже звон, появляющийся из-за ограниченности спектра, хорошо слышен. Ниже приведен пример звучания «косинусоидального» и «синусоидального» сигналов, следующих друг за другом с небольшим интервалом. Если зациклить такой фрагмент, то можно настроиться на выявление малейших отличий.
Отличия (если нет перегруза, а звуковоспроизводящая аппаратура обладает высоким качеством) не обнаруживаются – несмотря на то, что формы сигналов кардинально различаются. Не будет разницы и если понизить частоту:
Так в чем вопрос? – спросите вы. А в том, что мы рассмотрели только два частных случая, а в жизни их существует бесчисленное множество. И некоторые могут выбиваться из правила.
Не будем изобретать что-то изощренное, а просто смоделируем распространение звука в дисперсной среде – такой, где скорость распространения зависит от частоты. Простейший случай – когда высокие частоты распространяются быстрее низких по пропорциональному закону. Сигнал при этом будет описываться такой функцией:
где k – достаточно малое число. Назовем его «коэффициент дисперсии», а физический смысл заключается в степени зависимости фазового сдвига гармоники от ее номера. Величине 0 соответствует отсутствие фазовых сдвигов, величине 0,25 (это уже чрезвычайно много) – набег на четверть периода для каждой последующей гармоники (имеется в виду период результирующего сигнала), величине 0,5 (это колоссально много) – набег на половину периода, а величине 1,0 (это уже неприлично много) – набег на целый период. Отрицательным значениям соответствует ситуация, когда высокие частоты распространяются медленнее низких.
Вот как выглядит постепенное увеличение k:






Попутно замечаем, что амплитуды «волн» выравниваются, а следовательно, запас по амплитуде растет (немного не доходит до 4-х кратного).
А теперь послушайте, как звучит этот «размазанный» сигнал. Как и в предыдущем случае, для сравнения в фонограмму добавлен второй сигнал, в качестве которого взят исходный (с k =0). Итог – на 200 и 800 Гц отличий нет (на 200 Гц при использовании хороших головных телефонов, может, кто-то и отметит едва уловимую разницу), а вот на 40 Гц отличие становится заметным даже неискушенному слуху.
Здесь можно было бы остановиться (для опровержения достаточно одного контрпримера), либо рассмотреть другие экзотические случаи, но мне стало интересно – что же будет дальше?
А дальше импульс «расползается» настолько сильно, что затрагивает уже несколько последующих периодов. В результате сигнал становится похожим на случайный (внутри периода, конечно):

Дальнейшее увеличение k ничего нового не дает – характер картинки остается тот же. Все те же волны, возникающие случайно на разных местах и с разными амплитудами. Между тем, меняя k, можно наткнуться на несколько «магических» значений, при которых хаос неожиданно сменяется некоторым порядком. Вот самые яркие случаи:

Пример звучания (k=0,25):
– 40 Гц

А при k=1 вообще получается исходный сигнал (а чего вы ждали – это напрямую следует из формулы)!
Выяснилось, что упорядочивание происходит при k, равном отношению целых чисел (2/3, 3/4 и т.д.). Вспоминая Архимеда, Леонардо да Винчи и прочих великих математиков древности, любивших играться с числами, можно предположить, что наименьшую упорядоченность даст «золотое сечение» (G=[корень(5)-1]/2 = 0,61803..), либо его производные (G/2, G/3, 1/G, 1/2G и т.д.). Соответствующий случай приведен ниже.

Я перестал приводить примеры для 200 и 800 Гц, т.к. отличий в звучании все равно нет. Вместо этого в последнем случае добавился пример для 20 Гц – чтобы разница проявилась во всем своем блеске. Чтобы сравнить звучания сигналов с разными k между собой (а не с эталонным сигналом), используйте звуковые редакторы и команды «вырезать»–«вставить». Таким же способом можно размножить фрагмент – чтобы не использовать зацикливание.
На этом пока, собственно, все. На низких частотах прослеживается зависимость тембра звука от фазовых соотношений. Помимо спектрального анализа орган слуха начинает вовлекать другой механизм, суть которого, по-видимому, заключается в прямом восприятии пульсаций. Также показано, как можно создать звуковой сигнал с широким спектром, но не имеющий высоких «выбросов». Выигрыш по сравнению с импульсным сигналом достигает почти четырех раз (для данного случая), однако к этому следует подходить с осторожностью, т.к. на низких частотах меняется тембр.
Спектральная музыка
Спектра́льная му́зыка (также «спектрализм», фр. Musique spectrale ) — вид современной музыки, характерной особенностью которого является техника музыкальной композиции, опирающаяся на анализ звукового спектра создаваемого произведения. Выполняя подобный анализ на компьютере, композитор может использовать программное обеспечение, использующее дискретное преобразование Фурье, быстрое преобразование Фурье и спектрограммы. Спектральная композиция рождается из манипуляций с различными параметрами, полученными в результате такого анализа.
Содержание
История
Среди композиторов-предшественников спектральной композиции можно выделить Клода Дебюсси, Эдгара Вареза, Джачинто Шельси, Оливье Мессиана, Дьёрдя Лигети, Яниса Ксенакиса и Карлхайнца Штокхаузена. Кроме них, теоретически спектральную музыку осмысляли также Гарри Парч, Генри Коуэлл и Пауль Хиндемит.
Спектральная музыка как особое течение зарождается в 1970-е годы во Франции (в кругу композиторов, принадлежащих к Groupe de l’Itinéraire и вдохновлявшихся работами Мориса Равеля и Оливье Мессиана), в Германии (среди членов кёльнского ансамбля Feedback) и Румынии (среди композиторов, примыкавших к Hyperion Ensemble). Их гармонии и оркестровки основывались на гармонических обертонах сложных созвучий (таких как органные аккорды, колокольные тона и пение птиц).
Спектральная музыка являлась реакцией на престижный в то время сериализм и пост-сериализм, заявив о себе как об авангардном течении со своими собственными, уникальными композиторскими техниками.
Понятия. Диета для динамиков. Спектр музыкального сигнала. Какой он на самом деле?
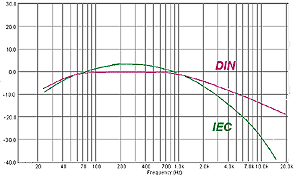
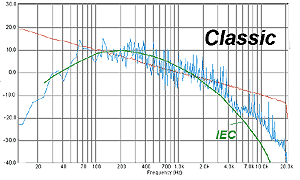
Кривые стандартной спектральной плотности: старая, «филармоническая» (зеленая) и новая (фиолетовая).
В пасторальных ранних 60-х эксперты смотрели в основном в филармоническую сторону, и утвержденная высокими подписями и печатями стандартная кривая спектра музыкальных записей по большей части основывалась на записях классической музыки. В конце 60-х, когда «Битлз» уже почти все отыграли, а другие как раз разошлись не на шутку, стало ясно, что музыка изменилась. То есть не вся, а та, что составляла основную нагрузку для звукозаписывающих компаний и основную диету для динамиков. «Современная» (для тех времен) музыка требовала большей терпимости к повышенному содержанию верхних частот, волосатые гитаристы, топчущие фузы, и взмокшие ударники с двадцатью тарелками на душу ударного населения об этом позаботились. Новую, постреволюционную кривую утвердила МЭК, а чуть позже взяла на вооружение святая инквизиция международной стандартизации – германская контора промышленных стандартов DIN. Что принято DIN, то принято всеми, это проверено неоднократно. Прогрессивная кривая стандартного спектра DIN, ныне принятая всеми, – на том же графике, лиловым цветом.
Культурная революция в конце 60-х изменила частотную характеристику.
Понимание вот этих вот кривых, хоть прошлой, классической, хоть новой, хипповой, уже само по себе проливает свет на посулы производителей насчет мощности. 100 Вт (или сколько там) максимальной мощности, указанной для динамика, не означает, не означало и никогда, до следующей культурной революции, не будет означать, что на него можно подать сигнал любой частоты в пределах заявленной рабочей полосы с мощностью, заявленной производителем, и ожидать, что все будет в порядке. На каких-то частотах, скорее всего, так и будет. А на других – нет, но теперь вы знаете, что вам этого и не обещали, в суде дело не пройдет.
Теперь третье условие измерения, оказавшееся, увы, для чересчур многих довольно дорогостоящим. Это касается ВЧ-излучателей. Пищалок, короче. На третьей странице (из семи) официального текста стандарта МЭК содержится фраза: «для излучателей, предназначенных для работы в пределах части звукового диапазона, измерение мощности производится на входе фильтра, выделяющего необходимую полосу частот». Нудно сказано, спору нет. Но суть-то вот в чем. Предположим, что у вас есть пищалка, для которой указано: рабочая полоса частот 2 – 20 кГц. По стандарту (стандарт – святое, особенно если в результате его приложения цифры становятся красивше) надо подключать пищалку через фильтр, пропускающий частоты выше 2 кГц, а амплитуду (и мощность, следовательно) мерить НА ВХОДЕ фильтра. Тогда получится: на входе – вся мощность, соответствующая стандартной кривой распределения по спектру, как на графике. То есть на средних – много, на нижних – тоже, а на верхние частоты спектра приходится с гулькин нос. Этот нос и попадает на пищалку, и она прекрасно себя чувствует.
Наиболее компетентные (и, как следствие, наиболее добросовестные) производители приводят показатели мощности и на входе, и на выходе стандартного фильтра. И указывают (дальше – цитата из профессиональной техдокументации Philips): «Максимально допустимая мощность (на входе/выходе фильтра) – 20/4 Вт (фильтр 2000 Гц, 12 дБ/окт.) или 50/6 Вт (фильтр 4000 Гц, 12 дБ/окт.)». Для специалистов-то ясно: в числителе – на входе фильтра, в знаменателе – на выходе. Разницу почувствовали, или как? В бумажке, прикладываемой к динамику, уж будьте любезны, вам напишут только числитель. В числителе – лютая мощность широкополосного сигнала, приходящего на фильтр кроссовера, выделяющий сигнал для пищалки. Фильтр из всего этого на входе вырезает (в соответствии со своими характеристиками) малую долю верхнечастотных составляющих, предназначенных для воспроизведения ВЧ-головкой. Уже благодаря стандартизованному спектру там не бог весть сколько остается от общей мощности. А после фильтра – ну сами приложите линейку к графику и увидите, сколько. Динамику предстоит переваривать и выносить как раз знаменатель дроби, приводимой честным производителем. А вот сколько было сожжено пищалок в ходе этой вечной войны числителя со знаменателем – сказать невозможно, а выплатить ущерб – еще труднее. Практический вывод: при прочих равных жизнестойкость пищалки напрямую связана с характеристиками фильтра, через который она подключена. В большей степени, чем с характеристиками самой пищалки как образца инженерной мысли.
Сколько же было сожжено пищалок в ходе вечной войны числителя со знаменателем.
Ну, это – стандарт, эталон, принцип и усредненный ориентир. А как по жизни-то, в смысле – «чисто-конкретно», на основаниях живого музыкального материала. Давайте посмотрим: вот кривая спектрального распределения амплитуды сигнала, усредненная по приблизительно 20 компакт-дискам с записями музыки классического жанра: по большей части – в исполнении полного состава симфонического оркестра.
На графике – усредненный спектр классической музыки (долго копили и усредняли) – это синяя кривая. Красная – спектральная характеристика розового шума. Она будет всюду присутствовать на дальнейших графиках, чтобы служить ориентиром. Поскольку спектр розового шума – образец равномерного распределения энергии по октавным полосам. Спектр розового шума в наших опытах снимался с того же CD-проигрывателя, что и остальные фонограммы, так что есть уверенность, что тракт пропускает все частоты исследуемого диапазона. (Запись розового шума использовалась с диска IASCA Competition. Качество сигнала не нуждается в комментариях – и так все видно. Для сведения экспериментаторов: мы пробовали несколько записей на тестовых дисках, обозначенных как розовый шум, но по-настоящему равномерная характеристика обнаружилась только на IASCA, Competition или Setup&Test, не важно, запись одинаковая.)
Возвращаясь к графику. Посмотрите: действительно, распределение мощности по спектру очень похоже на то, что предлагалось (до 1969 года) Международной Электротехнической на верхних частотах, правда, современные записи дают больше амплитуды, чем ожидалось, но этот фактор мы оценим позже, на особом материале. Теперь – к року, под напором которого в 1969 году кривая «музыки всех времен» была откорректирована.
«Races» в исполнении Yello – эталон равномерного распределения энергии.
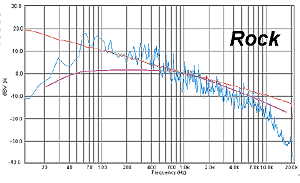
Усредненная, нашими усилиями, спектральная характеристика рок-записей (от Dire Straits до AC/DC) – на графике. Здесь на верхних частотах музыка даже недотягивает до «дисциплинирующей» кривой стандартного спектра. Зато на нижних показывает: мощность реального сигнала может быть заметно выше, чем предполагается по стандарту.
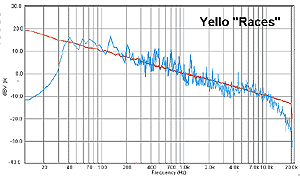
Чуть, может быть, отвлекаясь от общего плана повествования, покажем еще одну АЧХ, уж очень характерной она оказалась. Мало какая презентация, шоу или прочий перформанс с имиджем и вручением призов проходит сейчас без исполнения произведения группы Yello под названием «Races». Действительно – очень эмоционально и захватывающе. Мы при тестовых прослушиваниях аппаратуры всегда включаем эту фонограмму в репертуар, поскольку на ней многое слышно. Однако, только сняв спектрограмму, стало ясно, хотя бы отчасти, откуда такая наполненность. Посмотрите, вещь редкая.
Оказалось, что спектр «Races» в исполнении Yello практически без отклонений повторяет спектр розового шума – эталона равномерного распределения энергии. Так что ценность этой записи для тестирования аудиоаппаратуры не просто подтвердилась, а получила (почти случайно) естественнонаучное обоснование.
Такой инструмент будет в ЛЮБОЙ аудиосистеме воспроизводиться как минимум двумя динамиками в каждом канале.
Однако в целом наука недалеко отдалилась от реальности по части спектра, и поэтому стандартные кривые могут быть положены в основание такого важнейшего, по всем статьям, фактора в проектировании автомобильной аудиосистемы, как распределение мощности по полосам частот. Это наиболее важно именно для автомобильных систем, где поканальное усиление – вещь далеко не экзотическая. Справа от «Yello» – кривая рекомендованного распределения мощности по частотным каналам, основанная на «старой» и на «новой» кривых стандартного музыкального спектра.
Вот вам, и будьте любезны! Ни в чем противоправном не замеченная, Дайана Кролл при измерениях по пиковой шкале показала, что на ВЧ-полосу (выше 3 кГц) временами приходится больше 50% мощности. Так что принятая и очень комфортная для конструкторов аудиоаппаратуры школа маломощных ВЧ-каналов при многополосном усилении современных записей с большой динамикой может дать сбой и явно выиграет от критического взгляда. Практическая рекомендация: пиковую мощность ВЧ-канала многополосной системы при достаточно низкой частоте раздела СЧ/ВЧ (типа 3 кГц, ниже у нас уже не бывает) надо выбирать одного порядка с мощностью СЧ-канала.
Комфортная школа маломощных ВЧ-каналов мало приспособлена к современным записям с большой динамикой.
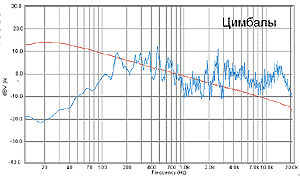
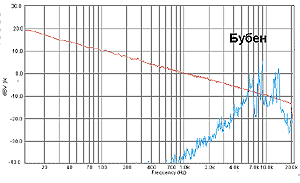
А насколько далеко и насколько энергично проникают музыкальные инструменты в верхнечастотную область? Не вдаваясь в ситуацию выше 20 кГц, куда уж там, ограничимся тем, что творится в привычном нам звуковом диапазоне. Вот, например, академические оркестровые цимбалы. Кто последний раз в консерватории был никогда, поясним: цимбалы – это тарелки, которые музыкант держит в руках (с помощью петель на тыльной стороне тарелок) и по сигналу дирижера шарашит ими друг об дружку, придавая драматизм исполнению произведения в соответствии с замыслом автора. Звучат цимбалы, с точки зрения спектра частот – вот так, как на графике.
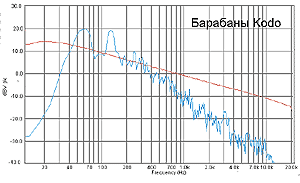
Даже огромные японские барабаны Kodo бьют в основном в полосе 40 – 60 Гц.
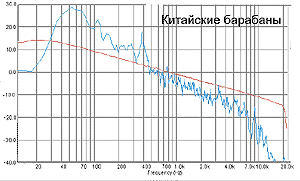
Китайский вариант басовых барабанов. Уже ниже, но н е так, как можно было подумать.
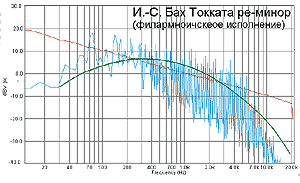
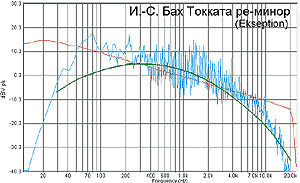
Популяризованное исполнение токкаты. Мидбасов – больше, суббасов – меньше, а с верхними частотами – история совсем грустная.
А вот в конце тех же 60-х был такой ансамбль из Голландии под названием Ekseption. (Это не опечатка, пишется именно так.) Они первыми, или почти первыми, начали популяризировать классические музыкальные произведения, сочетая филармонические инструменты с современными для 60-х. Токката ре-минор (автор – И.С. Бах, аранжировка Р. Ван ден Линден) всегда была визитной карточкой Ekseption. Спектр их визитной карточки – слева.
Забавно, что на характере спектрограммы в большей степени сказались следы прогресса в деле звукозаписи за последние 30 лет, нежели популяризация исполнения. Спектр на нижних частотах – более «доходчивый», чем при классическом исполнении, нетрудных для прочтения простой аппаратурой мидбасов полно, а серьезных низких – совсем даже не очень. А вот на верхних частотах, несмотря на то, что к баховской партитуре щедрой рукой герра Ван ден Линдена были добавлены ударные, энергия существенно скромнее того, что сейчас записывается. А уж как мы в свое время совели от линденовских тарелочек, казалось – уж шире полосы записи не бывает. А она, как выяснилось, вот какая, выше 10 кГц – слезы, да и только. Ничто так не старит, как годы.
Однако вернемся к басам, это голландцы и ностальгия отвлекли, общими усилиями. Итак, первое заключение, которое мы имеем право сделать: реальный музыкальный сигнал существенных составляющих ниже 30 – 40 Гц почти никогда не содержит. А раз так, то и характеристики сабвуфера надо оптимизировать под реальный сигнал, а не под математическую абстракцию.
В этой связи в несколько новом свете предстает столь распространенное устройство для подъема басов в усилителях – bass boost, который практически всегда настроен на частоты между 40 и 45 Гц. На первый взгляд устройство – не царских кровей, типа – для долбежки, в ущерб музыкальности. А теперь давайте посмотрим непредвзято: подъем частот на 40 Гц означает их (относительное) ослабление на частотах ниже 40, 30 и так далее. Значит, если организовать АЧХ сабвуфера с разумным спадом к 40 Гц, а затем приподнять АЧХ на этой отметке, то есть шанс получить частотную характеристику, оптимизированную по отношению к спектру реального музыкального сигнала.
В свете реального музыкального спектра распространенное устройство bass boost начинает выглядеть по-другому.
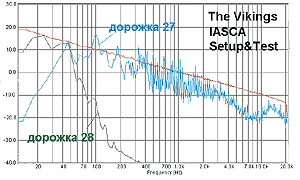
На соревнованиях по автозвуку возможности аудиосистемы по части суббасовых частот оцениваются по одной и той же стандартной фонограмме с судейского диска IASCA Competition. Это – запись произведения под названием «The Vikings», выполненная в музыкальном центре имени Мортона Майерсона в Далласе, штат, сами понимаете, Техас. Чудовищного размера (как сообщается в сопроводительной брошюре) орган, играющий в очень большом помещении, производит величественные звуки. Спектр, отражающий это величие, – внизу слева.
Спору нет, здесь суббасовые частоты – в изобилии. Амплитуда сигнала даже на 10 Гц более чем существенная. Система, способная не напрягаясь отыграть то, что записано на этой дорожке судейского диска, действительно заслуживает призов и наград. Но посмотрим на все это практичным взором. Тем более что составители диска нам в этом сами помогли. На настроечном диске Setup&Test, записанном в лаборатории Sheffield также по заказу IASCA, есть еще два варианта «Викингов». На одном из них исходная запись подверглась процедуре «обрезания» нижних частот фильтром шестого порядка с частотой среза 50 Гц. Результат – на дорожке 27 диска IASCA Setup&Test. На следующей дорожке записано то, что изъято из исходной фонограммы в результате небезболезненной процедуры.
«The Vikings»: эталонная запись для оценки суббасов на соревнованиях во всем мире.
Слушателю предлагается оценить, насколько изменилось звучание его системы при воспроизведении нетронутой фонограммы, содержащей весь спектр частот, и «обрезанной». Как правило, разница слышна. В большом числе случаев (не во всех, но в большом числе) отфильтрованная запись звучит лучше. Но побеждают те, у кого лучше звучит неотфильтрованная, ведь только она содержится на судейском диске.
Многие великолепно звучащие аудиосистемы не воспроизведут того, что записано на судейском диске IASCA. Правда, это не записано больше нигде. Или почти нигде.
Но теперь взгляните: отфильтрованная фонограмма по своему спектральному составу на удивление близка к спектру «нормальной» (типичной, ожидаемой, назовите как угодно) записи. Получается, что требования к «спортивной» установке и к обычной, мягко говоря, не совсем совпадают. С одной стороны, это оправдано: судейская запись предъявляет повышенные требования к системе, как полагается на соревнованиях. А с другой стороны, многие великолепно звучащие аудиосистемы в таком соревновании проиграют, ибо не воспроизведут того, что записано на судейском диске и не записано больше нигде. Или почти нигде. Вот теперь про это «почти».
Так что же, не бывает в звукозаписи частот, достойных названия суббасовых? Да нет же, бывает. Только не совсем там, где мы искали. Прежде всего, предлагаю вам согласиться с тем, что, с учетом звуковых реалий, сабвуфер в машине, строго говоря, является не «саб-», а просто «вуфером», то есть низкочастотным динамиком, призванным дополнять в области низких частот малогабаритную фронтальную акустику. А сабвуфер в истинном смысле слова – атрибут домашнего театра, где на него возлагаются задачи воспроизведения звуков не музыкального, а природно-техногенного происхождения. Вот вам пример. «Нормальный летний дождь», вернее – нормальная летняя гроза, аккуратно записанная Аланом Парсонсом для студии Telarc. Ее спектр – ниже.
Обыкновенный гром содержит суббасовых частот больше, чем любая музыкальная фонограмма.
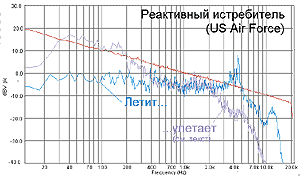
Звук реактивного истребителя, пролетающего над головой и уходящего «в сторону моря». Хорошо, что это не бомбардировщик, а то кривая была бы только одна
На фоне немудреного природного явления возможности музыкального центра в Далласе представляются пределом деликатности.
Звуки с такими характеристиками – принадлежность природы и техники. Стало быть, появляются они, как правило, в контексте видеоряда, то есть – вне типичной автомобильной аудиосистемы. Есть, однако, считанные, но очень эффектные исключения. Петр Ильич Чайковский в порыве вдохновения и патриотизма вписал в партитуру «Увертюры 1812 года» партию для артиллерии. Оттого-то это произведение в полной оркестровке исполняется нечасто, боеприпасы в смете расходов большинства симфонических оркестров не предусмотрены. Но уж когда «Увертюра» исполняется, частоты появляются знатные. Вот спектр одной из лучших существующих записей этого произведения. Половина лавров по праву – Петра Ильича, а половина – студии Telarc.
Увертюра 1812 года с пушками и без. Партия артиллерии делает эту запись уникальной по содержанию инфразвука.
До одиннадцатой минуты спектр инструментов большого, энергично играющего, но все же обычного симфонического оркестра, тоже обычный. А когда на 11-ой минуте шарахают пушки на дымном порохе (согласно партитуре, при П.И. бездымного еще не было), появляется имеющая немного равных по амплитуде добавка к спектру инфранизких частот.
Это произведение в полной оркестровке исполняется нечасто, боеприпасы в смете расходов не предусмотрены.
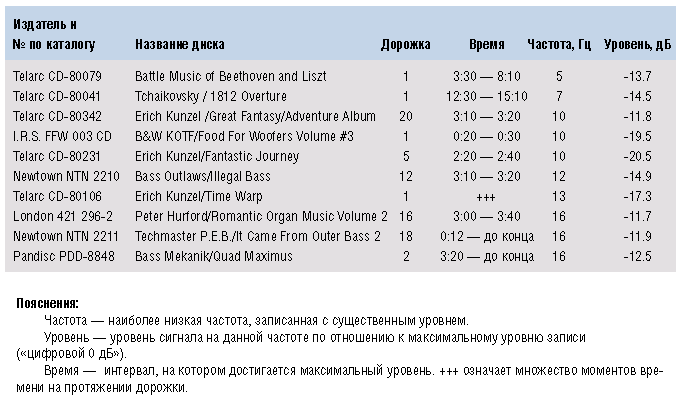
Не случайно хорошие записи «Увертюры 1812 года» находятся на самом верху списка самых басовых компакт-дисков, составленного в свое время в акустической лаборатории Оклендского университета. В таблице на обороте – первые 10 позиций этого списка.
Обратите внимание: специализированных «басовых» дисков в таблице мало, и они далеко не возглавляют список, упорядоченный по возрастанию наинизшей частоты, присутствующей в записи. Первый басовый диск – на четвертом месте в таблице, а тот, что составил материал для SPL-фонограмм судейского диска IASCA – только на 10-м. Дело в том, что «эспиэльные» диски – это, как правило, не про суббас, это про другое.
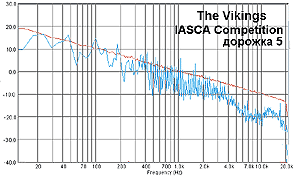
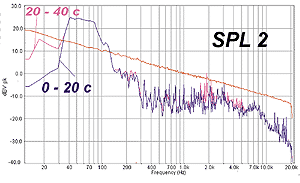
Там же есть спектрограмма одной из эспиэльных дорожек (второй по счету) с диска IASCA Competition.
В течение первых 20 секунд львиная доля энергии сосредоточена в полосе 40 – 80 Гц. И только в течение следующих 20 с добавляются инфранизкочастотные составляющие, на случай, если так настроена басовая акустика. На остальных трех SPL-дорожках (первой, третьей и четвертой) таких низких частот вообще нет, лучше не ищите, а поверьте на слово.
Вместо заключения
У комара длинный нос, чтобы сосать кровь, у кита – усы, чтобы фильтровать планктон, у акулы – 12 рядов зубов, чтобы лопать рыбу. Эволюция приспособила биологические виды к положенной им диете. Аудиосистемы не порождение природы или Создателя, о них придется позаботиться нам с вами. Задача почетная, ставящая конструктора на одну ступень с природой или Создателем. Мы в этой публикации ставили задачу снабдить читателя (если он в какой-то степени конструктор аудиосистемы) фактами, а не конкретными рецептами, предполагая, что это уж он нам не доверит. Однако трудно удержаться от того, что идет прямо в руки. Вот посмотрите: спроектировав сабвуфер так, чтобы он эффективно воспроизводил частоты выше 30 Гц, а ниже не воспроизводил ничего, вы лишите себя возможности оценить всю полноту звучания примерно трех музыкальных произведений из сотен тысяч существующих в записи. А жизнь и себе, и сабвуферу облегчите существенно.
Специальная запись для соревнований по SPL. На каких частотах в основном соревнуются – видно невооруженным глазом.
Или другой ориентир. Если учесть реальный спектр музыкального сигнала, то окажется, что в многополосной системе уровень сигнала, подведенного к пищалкам – самому уязвимому звену акустики, от порядка разделительных фильтров зависит сильнее, чем от чего бы то ни было еще. Это – реальный резерв, если правильно воспользоваться. Впрочем, последнее выводит нас на разговор о кроссоверах и о том, что от них зависит, а это разговор отдельный и непростой. В другой раз.
Источник: журнал Автозвук, 11/2000. Андрей Елютин