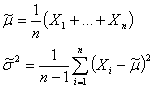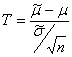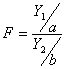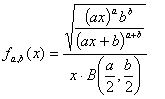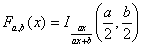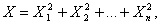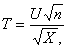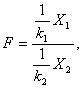Что такое распределение стьюдента

Конспект курса «Основы статистики»

1. Введение

Способы формирования репрезентативной выборки:

Простая случайная выборка (simple random sample)

Стратифицированная выборка (stratified sample)

Групповая выборка (cluster sample)

Типы переменных:

непрерывные (рост в мм)

дискретные (количество публикаций у учёного)

Ранговые (успеваемость студентов)

Гистограмма частот:

Позволяет сделать первое впечатление о форме распределения некоторого количественного признака.

Описательные статистики:

Меры центральной тенденции (узкий диапазон, высокие значения признака):

( используется для среднего значения из выборки, а для генеральной совокупности латинская буква )

Свойства среднего:

Если к каждому значению выборки прибавить определённое число, то и среднее значение увеличится на это число.

Если к каждому значению выборки прибавить определённое число, то и среднее значение увеличится на это число.

Если для каждого значения выборки, рассчитать такой показатель как его отклонение от среднего арифметического, то сумма этих отклонений будет равняться нулю.

Меры изменчивости (широкий диапазон, вариативность признака):

При добавлении сильно отличающегося значения данные меняются сильно и могут быть некорректные.

Дисперсия генеральной совокупности:

(среднеквадратическое отклонение генеральной совокупности)

(среднеквадратическое отклонение выборки)

Свойства дисперсии:

Квартили распределения и график box-plot

Нормальное распределение

Отклонения наблюдений от среднего подчиняются определённому вероятностному закону.

Стандартизация

Правило «двух» и «трёх» сигм

Центральная предельная теорема

Есть признак, распределенный КАК УГОДНО* с некоторым средним и некоторым стандартным отклонением. Тогда, если выбирать из этой совокупности выборки объема n, то их средние тоже будут распределены нормально со средним равным среднему признака в ГС и стандартным отклонением .

30″ alt=»SE = \frac<\sqrt>, n>30″ src=»https://habrastorage.org/getpro/habr/upload_files/20c/135/3bc/20c1353bcfedf2ff8851752cf7f49f37.svg»/>

Доверительные интервалы для среднего

Доверительный интервал является показателем точности измерений. Это также показатель того, насколько стабильна полученная величина, то есть насколько близкую величину (к первоначальной величине) вы получите при повторении измерений (эксперимента).

Идея статистического вывода

2. Сравнение средних

T-распределение

Если число наблюдений невелико и \sigma неизвестно (почти всегда), используется распределение Стьюдента (t-distribution).

Унимодально и симметрично, но: наблюдения с большей вероятностью попадают за пределы от

«Форма» распределения определяется числом степеней свободы ().

С увеличением числа распределение стремится к нормальному.

t-распределение используется не потому что у нас маленькие выборки, а потому что мы не знаем стандартное отклонение в генеральной совокупности.

Сравнение двух средних; t-критерий Стьюдента

Критерий, который позволяет сравнивать средние значения двух выборок между собой, называется t-критерий Стьюдента.

Условия для корректности использования t-критерия Стьюдента:

Две независимые группы

Формула стандартной ошибки среднего:

Формула числа степеней свободы:

Формула t-критерия Стьюдента:

Переход к p-критерию:

Проверка распределения на нормальность, QQ-Plot

Однофакторный дисперсионный анализ

Часто в исследованиях необходимо сравнить несколько групп между собой. В таком случае применятся однофакторный дисперсионный анализ.

Группы:

Нулевая гипотеза:

Альтернативная гипотеза:

Среднее значение всех наблюдений:

Общая сумма квадратов (Total sum of sqares):

Показатель, который характеризует насколько высока изменчивость данных, без учёта разделения их на группы.

Число степеней свободы:

— Межгрупповая сумма квадратов (Sum of sqares between groups)

— Внутригрупповая сумма квадратов (Sum of sqares within groups)

F-значение (основной статистический показатель дисперсионного анализа):

При делении значения межгрупповой суммы квадратов на число степеней свободы, полученный показатель усредняется.

Поэтому формула F-значения часто записывается:

Множественные сравнения в ANOVA

Проблема множественных сравнений:

Поправка Бонферрони

Самый простой (и консервативный) метод: P-значения умножаются на число выполненных сравнений.

Критерий Тьюки

Критерий Тьюки используется для проверки нулевой гипотезы против альтернативной гипотезы , где индексы и обозначают любые две сравниваемые группы.

Указанные сравнения выполняются при помощи критерия Тьюки, который представляет собой модифицированный критерий Стьюдента:

где — рассчитываемая в ходе дисперсионного анализа внутригрупповая дисперсия.

Многофакторный ANOVA

При применении двухфакторного дисперсионного анализа исследователь проверяет влияние двух независимых переменных (факторов) на зависимую переменную. Может быть изучен также эффект взаимодействия двух переменных.

Исследуемые группы называют эффектами обработки. Схема двухфакторного дисперсионного анализа имеет несколько нулевых гипотез: одна для каждой независимой переменной и одна для взаимодействия.

Условия применения двухмерного дисперсионного анализа:

Генеральные совокупности, из которых извлечены выборки, должны быть нормально распределены.

Выборки должны быть независимыми.

Дисперсии генеральных совокупностей, из которых извлекались выборки, должны быть равными.

Группы должны иметь одинаковый объем выборки.

АБ тесты и статистика

3. Корреляция и регрессия

Понятие корреляции

Коэффициент корреляции – это статистическая мера, которая вычисляет силу связи между относительными движениями двух переменных.

Принимает значения [-1, 1]

— показатель силы и направления взаимосвязи двух количественных переменных.

Знак коэффициента корреляции показывает направление взаимосвязи.

Коэффициент детерминации

— показывает, в какой степени дисперсия одной переменной обусловлена влиянием другой переменной.

Равен квадрату коэффициента корреляции.

Принимает значения [0, 1]

Условия применения коэффициента корреляции

Для применения коэффициента корреляции Пирсона, необходимо соблюдать следующие условия:

Сравниваемые переменные должны быть получены в интервальной шкале или шкале отношений.

Распределения переменных и должны быть близки к нормальному.

Число варьирующих признаков в сравниваемых переменных и должно быть одинаковым.

Коэффициент корреляции Спирмена

Регрессия с одной независимой переменной

Уравнение прямой:

— (intersept) отвечает за то, где прямая пересекает ось y.

— (slope) отвечает за направление и угол наклона, образованный с осью x.

Метод наименьших квадратов

Формула нахождения остатка:

— остаток

— реальное значение

— значение, которое предсказывает регрессионная прямая

Сумма квадратов всех остатков:

Параметры линейной регрессии:

Гипотеза о значимости взаимосвязи и коэффициент детерминации

Коэффициенты линейной регрессии

Коэффициенты регрессии (β) — это коэффициенты, которые рассчитываются в результате выполнения регрессионного анализа. Вычисляются величины для каждой независимой переменной, которые представляют силу и тип взаимосвязи независимой переменной по отношению к зависимой.

Коэффициент детерминации

— доля дисперсии зависимой переменной (Y), объясняем регрессионной моделью.

— сумма квадратов остатков

— сумма квадратов общая

Условия применения линейной регрессии с одним предиктором

Линейная взаимосвязь и

Нормальное распределение остатков

Регрессионный анализ с несколькими независимыми переменными

Множественная регрессия (Multiple Regression)

Множественная регрессия позволяет исследовать влияние сразу нескольких независимых переменных на одну зависимую.

Требования к данным

линейная зависимость переменных

нормальное распределение остатков

проверка на мультиколлинеарность

нормальное распределение переменных (желательно)

Источник

T-распределение Стьюдента

При этом оценка математического ожидания не равна в точности μ, а лишь колеблется вокруг этой величины. Разность истинного математического ожидания и рассчитанного на основе выборки, поделенная на масштабирующий коэффициент

имеет распределение, которое называется распределением Стьюдента с N степенями свободы. Есть и другие разделы статистики, в которых появляются случайные величины, распределенные по Стьюденту. Например, распределение Стьюдента используется при оценке значимости коэффициента корреляции Пирсона.

Чаще всего критерий Стьюдента применяется для проверки равенства средних значений в двух выборках.

Пример 1. Первая выборка — это пациенты, которых лечили препаратом А. Вторая выборка — пациенты, которых лечили препаратом Б. Значения в выборках — это некоторая характеристика эффективности лечения (уровень метаболита в крови, температура через три дня после начала лечения, срок выздоровления, число койко-дней, и т.д.) Требуется выяснить, имеется ли значимое различие эффективности препаратов А и Б, или различия являются чисто случайными и объясняются «естественной» дисперсией выбранной характеристики.

Пример 2. Первая выборка — это значения некоторой характеристики состояния пациентов, записанные до лечения. Вторая выборка — это значения той же характеристики состояния тех же пациентов, записанные после лечения. Объёмы обеих выборок обязаны совпадать; более того, порядок элементов (в данном случае пациентов) в выборках также обязан совпадать. Такие выборки называются связными. Требуется выяснить, имеется ли значимое отличие в состоянии пациентов до и после лечения, или различия чисто случайны.

Основные распределения, используемые в математической статистике:

F-распределение Фишера. Примеры использования распределения.

Если у нас есть две случайные величины, Y₁ и Y₂ , имеющие распределение хи-квадрат со степенями свободы a и b соответственно, то их отношение

имеет распределение, которое называется F-распределением со степенями свободы a и b. Также это распределение известно, как распределение Фишера.

Функция плотности вероятности F-распределения для некоторых a и b приведена на графике справа. Её аналитическая форма имеет вид:

Интегральная функция вероятности F-распределения имеет вид:

С помощью нормального распределения определяются три распределения, которые в настоящее время часто используются при статистической обработке данных. В дальнейших разделах книги много раз встречаются эти распределения.

где случайные величины X₁, X₂, X_n независимы и имеют одно и тоже распределение N(0,1). При этом число слагаемых, т.е. n, называется «числом степеней свободы» распределения хи – квадрат.

Распределение хи-квадрат используют при оценивании дисперсии (с помощью доверительного интервала), при проверке гипотез согласия, однородности, независимости, прежде всего для качественных (категоризованных) переменных, принимающих конечное число значений, и во многих других задачах статистического анализа данных.

Распределение t Стьюдента – это распределение случайной величины

где случайные величины U и X независимы, U имеет распределение стандартное нормальное распределение N(0,1), а X – распределение хи – квадрат с n степенями свободы. При этом n называется «числом степеней свободы» распределения Стьюдента.

В настоящее время распределение Стьюдента – одно из наиболее известных распределений среди используемых при анализе реальных данных. Его применяют при оценивании математического ожидания, прогнозного значения и других характеристик с помощью доверительных интервалов, по проверке гипотез о значениях математических ожиданий, коэффициентов регрессионной зависимости, гипотез однородности выборок и т.д.

Распределение Фишера – это распределение случайной величины

где случайные величины Х₁ и Х₂ независимы и имеют распределения хи – квадрат с числом степеней свободы k₁ и k₂ соответственно. При этом пара (k₁, k₂) – пара «чисел степеней свободы» распределения Фишера, а именно, k₁ – число степеней свободы числителя, а k₂ – число степеней свободы знаменателя. Распределение случайной величины F названо в честь великого английского статистика Р. Фишера (1890-1962), активно использовавшего его в своих работах.

Распределение Фишера используют при проверке гипотез об адекватности модели в регрессионном анализе, о равенстве дисперсий и в других задачах прикладной статистики.

Геометрическое распределение, параметры распределения

Источник