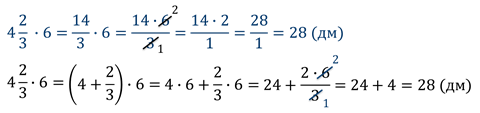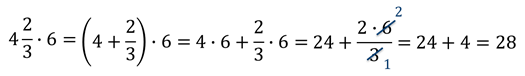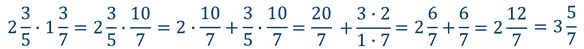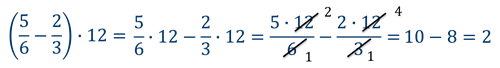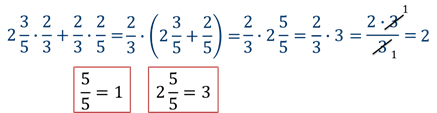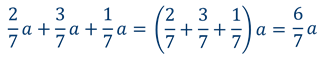Что такое распределительное свойство умножения 6 класс дроби
Урок 16 Бесплатно Применение распределительного свойства умножения
В этом уроке мы узнаем, как умножать смешанное число на натуральное, и разберем, как использовать распределительное свойство умножения для рационализации вычислений с обыкновенными дробями и смешанными числами.
Распределительное свойство умножения
Это свойство говорит нам о том, что если необходимо умножить одно число, назовем его a, на сумму двух других чисел, обозначим их b и c, то ответом будет сумма двух произведений: произведения a и b и произведения a и c
Вторая строка говорит о том же самом, что и первая; просто показывает, что коммутативное свойство умножения работает и в этом случае.
Умножение смешанного числа на натуральное используя распределительной свойство
В уроке «Умножение дробей» мы уже касались этих моментов. Теперь рассмотрим их более подробно.
Самый простой способ умножения смешанного числа на натуральное заключается в том, чтобы перевести смешанное число в натуральную дробь, домножив целую часть на знаменатель и прибавив его к числителю, а далее домножить полученную неправильную дробь на натуральное число, перемножив числитель дроби и натуральное число.
Это и будет результатом.
Пример:
Этот пример нам показывает, что даже такая простая операция, как умножение на 2, приводит нас к множеству умножений, сложений и даже делению. Для больших чисел такой путь неудобен. Стоит только представить, что целая часть смешанного числа будет больше 100, и знаменатель также также весьма сложный, то мы получим операции, которые с трудом делаются в уме.
Здесь нас выручит распределительное свойство.
Если представить \(\mathbf<43\frac<1><3>>\) как сумму его целой и дробной частей, то есть
\(\mathbf<43\frac<1><3>=43+\frac<1><3>>\), то нам нужно будет в дальнейшем умножать только 43 и \(\mathbf<\frac<1><3>>\), что значительно проще.
Посмотрим, как это все будет выглядеть целиком:
Можно заметить, что несмотря на то, что мы удлинили запись выражения, сами вычисления стали проще.
Может возникнуть необходимость выделения целой части, про это забывать нельзя. Но даже в таком случае делимое будет значительно меньше, чем если бы мы выносили целую часть из произведения, полученного классическим способом.
Пример:
Пройти тест и получить оценку можно после входа или регистрации
Урок-путешествие по математике «Применение распределительного свойства умножения» в 6-м классе
Разделы: Математика
Применение распределительного свойства умножения
Форма урока: Урок – путешествие.
Тип урока: Урок обобщения и систематизации знаний.
Методы обучения: фронтальная работа, самостоятельная работа, работа по вариантам.
Оборудование: компьютер, проектор, экран, листочки с числами от 1 до 9, презентация.
I. Организационный момент. Постановка целей урока.
Здравствуйте, ребята, садитесь. Сегодня у нас необычный урок, урок-путешествие. А отправимся мы с вами к острову “Дробей”. Но путешествие не обещает быть легким, ведь нам придется плыть по морю Сомнений, преодолев скалы Волнений, постараться не сесть на отмель Ошибок и не зацепить рифы Незнаний.
Давайте подумаем, чтобы путешествие было удачным, что нам надо взять с собой в дорогу, какие знания? (Ответы детей – правила умножения дробей, знание распределительного свойства умножения, и т. д.) Правильно, ребята, все это пригодится нам сегодня, мы повторим изученные правила и продолжим учиться применять их на практике.
II. Проверка домашнего задания.
Если х=1


Если х=



Ответ: 27
Итак, команда сформирована, отправляемся в путь!
III. Актуализация знаний. Устный счет.
IV. Тренировочные упражнения. Решение задач.
Кто решил №527 другим способом? Обсудить.
V. Закрепление знаний изученных правил.
Правильно решив задачи, мы не сели на отмель Ошибок и движемся дальше! (Корабль в пункте “2”) Предлагаю еще раз вспомнить правила действий с дробями. У вас на столах лежат листочки с цифрами от 1) до 9).
Я зачитываю вопрос, если он верный то напротив соответствующего номера ставите “+”, если неверный, то “-”.
Соедините знаки “+”, расположенные по одной линии. Что получили? Каким образом полученный символ связан с математикой? Где он нам встречается? Правильно, это х – неизвестное в уравнении. И, конечно, нам не миновать решения уравнений, если мы хотим добраться до цели нашего путешествия. Наш корабль тем временем перемещается в пункт “3”.
VI. Решение уравнений с использованием распределительного свойства умножения.
Дополнительные уравнения на карточках:
Вы замечательно справились и с этим испытанием, остался последний, самый опасный пункт – рифы Незнаний, желаю всем благополучно их преодолеть, выполнив задания самостоятельной работы, но перед этим предлагаю сделать небольшую паузу, послушать историческую справку.
Дроби появились в глубокой древности. При разделе добычи, при измерениях величин, да и в других похожих случаях люди встретились с необходимостью ввести дроби, так как результат измерений не всегда удавалось выразить натуральным числом, приходилось учитывать и части употребляемой меры.
Знание дробей считалось очень важным, ещё в первом веке до нашей эры выдающийся римский оратор и писатель Цицерон говорил: “Без знания дробей никто не может признаваться знающим арифметику!”
Наше обозначение обыкновенных дробей при помощи числителя и знаменателя было принято в Индии еще в VIII веке до н.э. однако без дробной черты. Только там писали знаменатель сверху, а числитель – снизу.
А записывать дроби в точности, как сейчас, стали арабы.
VII. Самостоятельная работа.
Задания из дидактического сборника. 1 вариант – стр 39, №127, №129, 2 вариант – стр 67, №127, №129.
VIII. Подведение итогов. Домашнее задание. Рефлексия.
Достигнув конечной точки нашего маршрута, давайте подведем итоги, насколько успешно мы разрешили встретившиеся на нашем пути проблемы? Кто с чем пришел к финишу?
Распределительное свойство умножения

Всего получено оценок: 146.
Всего получено оценок: 146.
Свойства умножения – это, прежде всего, возможность быстро произвести вычисление. Знание распределительного свойства поможет вам без проблем посчитать сложный пример или решить уравнение. Рассмотрим в в подробностях применение распределительного свойства умножения.
Умножение
Умножение – это сокращенный процесс сложения. Что это значит? Первый множитель это число, которое складывается само с собой число раз, равное второму множителю.
3*6=3+3+3+3+3+3=18 – вот как это выглядит на практике. Умножение было изобретено во время, когда потребовались большие вычисления, которые неудобно записывать в виде сложения.
Можно 3 раза сложить число 6, а можно 6 раз сложить число 3. Результат от этого не поменяется, в этом заключается смысл переместительного свойства умножения.
Умножение позволило решить достаточно много проблем, но вместе с ним в математику пришло и деление, как противоположная операция.
Свойства умножения
Всего у умножения 3 свойства:
Распределительное свойство
Распределительно свойство можно использовать для быстрого расчета. Рассмотрим большой пример для 6 класса с применением этого свойства умножения:
Обратите внимание, что пример представляет собой сумму слагаемых, каждый из которых представлен произведением. Рассмотрим каждое произведение в отдельности, а потом сложим результаты.
$$<1\over<2>>*18-<1\over<2>>*16=9-8=1$$ – такие ответы иногда бывают в сложных на вид примерах.
$$(<7\over<3>>+<56\over<3>>)=<63\over<3>>=21$$ – теперь воспользуемся распределительным свойством и умножим число 21 на каждое из чисел в скобках:
1+2+16-1=18 – вот такой маленький ответ получился в большом примере.
При решении этого примера, важно понять, что не всегда нужно использовать распределительное свойство умножения. Важно понимать, когда лучше им воспользоваться, а когда решить другим путем.
Что мы узнали?
Мы узнали, что такое умножение. Поговорили о свойствах умножения и особенно выделили распределительное свойство умножения. Решили большой пример на тему применения этого свойства.
Применение распределительного свойства умножения
Урок 15. Математика 6 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Применение распределительного свойства умножения»
Сегодня на уроке мы вспомним уже известное вам распределительное свойство умножения и применим его при решении задач и примеров.
Для начала давайте вспомним распределительное свойство умножения относительно сложения и относительно вычитания и запишем их в буквенном виде.
Итак, распределительное свойство умножения относительно сложения гласит, что для того чтобы умножить сумму на число, можно умножить на это число
каждое слагаемое и сложить получившиеся произведения.
Распределительное свойство умножения относительно вычитания говорит, что
для того чтобы умножить разность на число, можно умножить на это число
уменьшаемое и вычитаемое и из первого произведения вычесть второе.
Также мы с вами знаем, что с помощью распределительного свойства очень удобно упрощать выражения. А ещё мы помним, что распределительное свойство позволяет раскрывать скобки и выносить общий множитель за скобки.
Итак, мы вооружились знаниями распределительного свойства умножения, а значит, теперь можем приступить к изучению новой темы.
Муравей за одну минуту пробегает 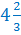
Но смотрите, эту задачу можно решить проще. Мы помним, что смешанное число это сумма целой и дробной части, значит, смешанное число можно записать в виде суммы. Что мы сейчас и сделаем.
Мы применили распределительное свойство умножения относительно сложения и упростили себе вычисления.
Чтобы умножить смешанное число на натуральное число, можно:
1) умножить целую часть на натуральное число;
2) умножить дробную часть на это натуральное число;
Помните, что всегда надо смотреть, как удобнее выполнять вычисления!
Правило умножения смешанных чисел:
Для того чтобы умножить смешанное число на смешанное число, можно:
1) перевести одно смешанное число в неправильную дробь;
2) умножить целую часть второго множителя на неправильную дробь;
3) умножить дробную часть второго множителя на неправильную дробь;
Найдите значение выражения:
Используя распределительное свойство умножения можно упрощать и буквенные выражения.
Итак, сегодня на уроке мы с помощью распределительного свойства умножения вывели правила умножения смешанных чисел.
Свойства умножения и деления
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Свойства умножения
Умножение — арифметическое действие, в котором участвуют два аргумента: множимый и множитель. Результат их умножения называется произведением.
Узнаем, какие бывают свойства умножения и как их применять.
Переместительное свойство умножения
От перестановки мест множителей произведение не меняется.
То есть, для любых чисел a и b верно равенство: a * b = b * a.
Это свойство можно применять к произведениям, в которых больше двух множителей.
Сочетательное свойство умножения
Произведение трех и более множителей не изменится, если какую-то группу множителей заменить их произведением.
То есть, для любых чисел a, b и c верно равенство: a * b * c = (a * b) * c = a * (b * c).
Сочетательное свойство можно использовать, чтобы упростить вычисления при умножении. Например: 25 * 15 * 4 = (25 * 4) * 15 = 100 * 15 = 1500.
Если не применять сочетательное свойство и вычислять последовательно, решение будет значительно сложнее: 25 * 15 * 4 = (25 * 15) * 4 = 375 * 4 = 1500.
Распределительное свойство умножения относительно сложения
Чтобы умножить сумму на число, нужно умножить на это число каждое слагаемое и сложить полученные результаты.
То есть, для любых чисел a, b и c верно равенство: (a + b) * c = a * c + b * c.
Это свойство работает с любым количеством слагаемых: (a + b + с + d) * k = a * k + b * k + c * k + d * k.
В обратную сторону распределительное свойство умножения относительно сложения звучит так:
Чтобы число умножить на сумму чисел, нужно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
Распределительное свойство умножения относительно вычитания
Чтобы умножить разность на число, нужно умножить на это число сначала уменьшаемое, затем вычитаемое, и из первого произведения вычесть второе.
То есть, для любых чисел a, b и c верно равенство: (a − b) * c = a * c − b * c.
В обратную сторону распределительное свойство умножения относительно вычитания звучит так:
Чтобы число умножить на разность чисел, нужно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.
Свойство нуля при умножении
Если в произведении хотя бы один множитель равен нулю, то само произведение будет равно нулю.
То есть, для любых чисел a, b и c верно равенство:
0 * a * b * c = 0.
Свойство единицы при умножении
Если умножить любое целое число на единицу, то в результате получится это же число.
То есть, умножение на единицу не изменяет умножаемое число: a * 1 = a.
Свойства деления
Деление — арифметическое действие обратное умножению. В результате деления получается число (частное), которое при умножении на делитель дает делимое.
Основные свойства деления целых чисел
И еще одно важное свойство деления, которое проходят в 5 классе:
Если делимое и делитель умножить или разделить на одно и тоже натуральное число, то их частное не изменится.
В буквенной форме это свойство выглядит так: a : b = (a * k) : (b * k), где k — любое натуральное число.
Применим свойства деления на практике.
Пример 1
Мама купила 6 кг конфет и разложила их в три пакета. Сколько килограммов конфет в каждом пакете?
Так как в каждом пакете одинаковое количество конфет, разделим 6 кг на три равные части: 6 : 3 = 2. Значит в каждом пакете по 2 кг конфет.
Пример 2
Вычислить: 500 * (100 : 5).
Как решаем: 500 * (100 : 5) = (500 * 100) : 5 = 50000 : 5 = 10000.
Ответ: 500 * (100 : 5) = 10000.
Пример 3
Упростить выражение: 27a – 16a.
Свойства умножения и деления помогают упрощать выражения. То есть, если запомнить эти свойства и научиться их применять, то решать задачки можно быстрее.