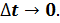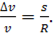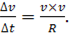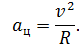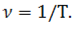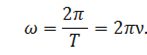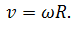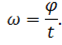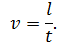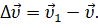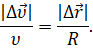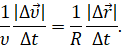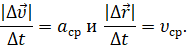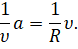Что такое равномерное движение точки по окружности

Кинематика. Равномерное движение по окружности.

Среди различных видов криволинейного движения особый интерес представляет равномерное движение тела по окружности. Это самый простой вид криволинейного движения. Вместе с тем любое сложное криволинейное движение тела на достаточно малом участке его траектории можно приближенно рассматривать как равномерное движение по окружности.

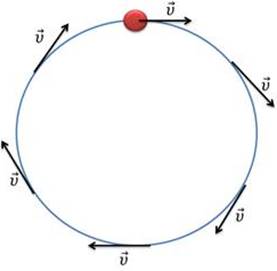
Такое движение совершают точки вращающихся колес, роторов турбин, искуственные спутники, вращающиеся по орбитам и т. д. При равномерном движении по окружности численное значение скорости остается постоянным. Однако направление скорости при таком движении непрерывно изменяется.

Скорость движения тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке. В этом можно убедиться, наблюдая за работой точила, имеющего форму диска: прижав к вращающемуся камню конец стального прута можно увидеть отрывающиеся от камня раскаленные частицы. Эти частицы летят с той скоростью, которой они обладали в момент отрыва от камня. Направление вылета искр всегда совпадает с касательной к окружности в той точке, где пруток касается камня. По касательной к окружности движутся также брызги от колес буксующего автомобиля.

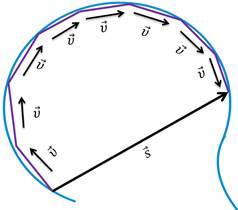
Таким образом, мгновенная скорость тела в разных точках криволинейной траектории имеет различные направления, тогда как модуль скорости может быть или всюду одинаковым, или изменяться от точки к точке. Но даже если модуль скорости не изменяется, ее все равно нельзя считать постоянной. Ведь скорость – величина векторная, а для векторных величин модуль и направление одинаково важны. Поэтому криволинейное движение всегда ускоренное, даже если модуль скорости постоянен.

При криволинейном движении могут изменяться модуль скорости и ее направление. Криволинейное движение, при котором модуль скорости остается постоянным, называют равномерным криволинейным движением. Ускорение при таком движении связано только с изменением направления вектора скорости.

И модуль, и направление ускорения должны зависеть от формы кривлинейной траектории. Однако нет необходимости рассматривать каждую из ее бесчисленных форм. Представив каждый участок как отдельную окружность с некоторым радиусом, задача нахождения ускорения при криволинейном равномерном движении сведется к отысканию ускорения при равномерном движении тела по окружности.

Равномерное движение по окружности характеризуется периодом и частотой обращения.

Время, за которое тело делает один оборот, называют периодом обращения.

При равномерном движении по окружности период обращения определяется делением пройденного пути, т. е. длины окружности на скорость движения:

Величина, обратная периоду, называется частотой обращения, обозначается буквой ν. Число оборотов в единицу времени ν называют частотой обращения:

Из-за непрерывного изменения направления скорости, движущееся по окружности тело имеет ускорение, которое характеризует быстроту изменения ее направления, численное значение скорости в данном случае не меняется.

При равномерном движении тела по окружности ускорение в любой ее точке всегда направлено перпендикулярно скорости движения по радиусу окружности к ее центру и называется центростремительным ускорением.

Поскольку угол равен отношению длины дуги АВ к радиусу R, получим

Выражение для модуля вектора ускорения а имеет вид:

Источник

Равномерное движение тела по окружности

1. Движением тела по окружности называют движение, траекторией которого является окружность. По окружности движутся, например, конец стрелки часов, точки лопасти вращающейся турбины, вращающегося вала двигателя и др.

При движении по окружности направление скорости непрерывно изменяется. При этом модуль скорости тела может изменяться, а может оставаться неизменным. Движение, при котором изменяется только направление скорости, а её модуль сохраняется постоянным, называется равномерным движением тела по окружности. Под телом в данном случае имеют в виду материальную точку.

2. Движение тела по окружности характеризуется определёнными величинами. К ним относятся, прежде всего, период и частота обращения. Период обращения тела по окружности ​ \( T \) ​ — время, в течение которого тело совершает один полный оборот. Единица периода — ​ \( [\,T\,] \) ​ = 1 с.

Связь между частотой и периодом обращения выражается формулой: ​ \( n=1/T \) ​.

Пусть некоторое тело, движущееся по окружности, за время ​ \( t \) ​ переместилось из точки А в точку В. Радиус, соединяющий центр окружности с точкой А, называют радиусом-вектором. При перемещении тела из точки А в точку В радиус-вектор повернётся на угол ​ \( \varphi \) ​.

Быстроту обращения тела характеризуют угловая и линейная скорости.

Угловая скорость ​ \( \omega \) ​ — физическая величина, равная отношению угла поворота \( \varphi \) радиуса-вектора к промежутку времени, за которое этот поворот произошел: ​ \( \omega=\varphi/t \) ​. Единица угловой скорости — радиан в секунду, т.е. ​ \( [\,\omega\,] \) ​ = 1 рад/с. За время, равное периоду обращения, угол поворота радиуса-вектора равен ​ \( 2\pi \) ​. Поэтому ​ \( \omega=2\pi/T \) ​.

Линейная скорость тела ​ \( v \) ​ — скорость, с которой тело движется вдоль траектории. Линейная скорость при равномерном движении по окружности постоянна по модулю, меняется по направлению и направлена по касательной к траектории.

Линейная скорость равна отношению пути, пройденному телом вдоль траектории, ко времени, за которое этот путь пройден: ​ \( \vec=l/t \) ​. За один оборот точка проходит путь, равный длине окружности. Поэтому ​ \( \vec=2\pi\!R/T \) ​. Связь между линейной и угловой скоростью выражается формулой: ​ \( v=\omega R \) ​.

Из этого равенства следует, что чем дальше от центра окружности расположена точка вращающегося тела, тем больше её линейная скорость.

4. Ускорение тела равно отношению изменения его скорости ко времени, за которое оно произошло. При движении тела по окружности изменяется направление скорости, следовательно, разность скоростей не равна нулю, т.е. тело движется с ускорением. Оно определяется по формуле: ​ \( \vec=\frac<\Delta\vec>\) ​ и направлено так же, как вектор изменения скорости. Это ускорение называется центростремительным ускорением.

Центростремительное ускорение при равномерном движении тела по окружности — физическая величина, равная отношению квадрата линейной скорости к радиусу окружности: ​ \( a=\frac \) ​. Так как ​ \( v=\omega R \) ​, то ​ \( a=\omega^2R \) ​.

При движении тела по окружности его центростремительное ускорение постоянно по модулю и направлено к центру окружности.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. При равномерном движении тела по окружности

1) изменяется только модуль его скорости
2) изменяется только направление его скорости
3) изменяются и модуль, и направление его скорости
4) не изменяется ни модуль, ни направление его скорости

2. Линейная скорость точки 1, находящейся на расстоянии ​ \( R_1 \) ​ от центра вращающегося колеса, равна ​ \( v_1 \) ​. Чему равна скорость ​ \( v_2 \) ​ точки 2, находящейся от центра на расстоянии ​ \( R_2=4R_1 \) ​?

1) ​ \( v_2=v_1 \) ​
2) ​ \( v_2=2v_1 \) ​
3) ​ \( v_2=0,25v_1 \) ​
4) ​ \( v_2=4v_1 \) ​

3. Период обращения точки по окружности можно вычислить по формуле:

1) ​ \( T=2\pi\!Rv \) ​
2) \( T=2\pi\!R/v \) ​
3) \( T=2\pi v \) ​
4) \( T=2\pi/v \) ​

4. Угловая скорость вращения колеса автомобиля вычисляется по формуле:

1) ​ \( \omega=a^2R \) ​
2) \( \omega=vR^2 \) ​
3) \( \omega=vR \)
4) \( \omega=v/R \) ​

5. Угловая скорость вращения колеса велосипеда увеличилась в 2 раза. Как изменилась линейная скорость точек обода колеса?

1) увеличилась в 2 раза
2) уменьшилась в 2 раза
3) увеличилась в 4 раза
4) не изменилась

6. Линейная скорость точек лопасти винта вертолёта уменьшилась в 4 раза. Как изменилось их центростремительное ускорение?

1) не изменилось
2) уменьшилось в 16 раз
3) уменьшилось в 4 раза
4) уменьшилось в 2 раза

7. Радиус движения тела по окружности увеличили в 3 раза, не меняя его линейную скорость. Как изменилось центростремительное ускорение тела?

1) увеличилось в 9 раз
2) уменьшилось в 9 раз
3) уменьшилось в 3 раза
4) увеличилось в 3 раза

8. Чему равен период обращения коленчатого вала двигателя, если за 3 мин он совершил 600 000 оборотов?

9. Чему равна частота вращения точки обода колеса, если период обращения составляет 0,05 с?

1) 0,05 Гц
2) 2 Гц
3) 20 Гц
4) 200 Гц

10. Линейная скорость точки обода велосипедного колеса радиусом 35 см равна 5 м/с. Чему равен период обращения колеса?

1) 14 с
2) 7 с
3) 0,07 с
4) 0,44 с

11. Установите соответствие между физическими величинами в левом столбце и формулами для их вычисления в правом столбце. В таблице под номером физической
величины левого столбца запишите соответствующий номер выбранной вами формулы из правого столбца.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
А) линейная скорость
Б) угловая скорость
В) частота обращения

ФОРМУЛА
1) ​ \( 1/T \) ​
2) ​ \( v^2/R \) ​
3) ​ \( v/R \) ​
4) ​ \( \omega R \) ​
5) ​ \( 1/n \) ​

12. Период обращения колеса увеличился. Как изменились угловая и линейная скорости точки обода колеса и её центростремительное ускорение. Установите соответствие между физическими величинами в левом столбце и характером их изменения в правом столбце.
В таблице под номером физической величины левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) угловая скорость
Б) линейная скорость
B) центростремительное ускорение

ХАРАКТЕР ИЗМЕНЕНИЯ ВЕЛИЧИНЫ
1) увеличилась
2) уменьшилась
3) не изменилась

Часть 2

13. Какой путь пройдёт точка обода колеса за 10 с, если частота обращения колеса составляет 8 Гц, а радиус колеса 5 м?

Источник

Равномерное движение точки по окружности

Урок 11. Физика 10 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Равномерное движение точки по окружности»

Движение тела по окружности довольно часто встречается в повседневной жизни. Взять хотя бы движение Земли вокруг своей оси или вокруг Солнца.

Кроме этого существуют ещё сотни примеров: вращение колеса автомобиля, вращение электронов вокруг ядра атома, движение стрелок часов и многое другое.

В первую очередь, давайте условимся, что называется равномерным движением по окружности? При прямолинейном движении мы говорили о том, что тело совершает одинаковые перемещения за равные промежутки времени. В случае с движением тела по окружности, равномерным движением называется такое движение, при котором тело поворачивается на одинаковые углы за равные промежутки времени.

Мы уже говорили о том, что мгновенная скорость направлена по касательной к траектории движения. Значит, при движении тела по окружности, его скорость будет направлена по касательной к этой окружности в данной точке. При этом, модуль скорости, так же, как и модуль ускорения остаётся постоянным, в то время как их направления постоянно меняются.

Из этого можно сделать вывод, что любое криволинейное движение является ускоренным, даже если модуль скорости остаётся постоянным.

Давайте рассмотрим ускорение при движении тела по кривой. Поскольку направление ускорения постоянно меняется, имеет смысл рассматривать мгновенное ускорение. Точно так же, как и в случае с мгновенной скоростью, мы будем брать все меньшие и меньшие промежутки времени.

Тогда, можем записать, что мгновенное ускорение — отношение изменения скорости к промежутку времени, за который это изменение произошло, при

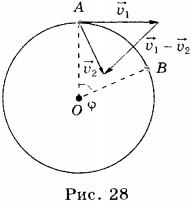
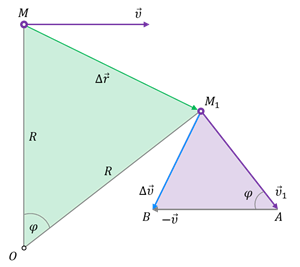
Возьмём две произвольные точки А и В, принадлежащие окружности. В обеих точках скорость будет направлена по касательной, а модуль скорости в точке A будет равен модулю скорости в точке B.

Воспользуемся теперь сложением скоростей, чтобы найти вектор показывающий направление изменения скорости. Рассмотрим два треугольника, показанные на рисунке. Один из этих треугольников образован двумя радиусами и вектором перемещения, а второй — двумя модулями скорости и вектором изменения скорости. Эти треугольники подобны, т.к. являются равнобедренными и имеют одинаковый угол при вершине. Напомним, что мы рассматриваем промежуток времени, стремящийся к нулю. В этом случае, угол поворота будет стремиться к нулю, а значит и угол между скоростью в точке A и скоростью в точке B — тоже будет стремиться к нулю.

Теперь разберёмся с модулем ускорения. Мы снова используем те же два треугольника. Поскольку треугольники подобны, мы можем записать, что

Перемещение мы можем записать как произведение скорости и времени:

Теперь преобразуем выражение:

Это, как раз, и будет модулем ускорения:

Таким образом, мы выяснили, что ускорение при движении по окружности направлено к центру и численно равно отношению квадрата скорости к радиусу окружности.

В завершении темы, вспомним несколько важных физических величин, описывающих криволинейное движение. В первую очередь, это, конечно, период обращения. Периодом обращения называется время, за которое тело совершает полный оборот.

Например, период обращения Земли вокруг Солнца равен одному году.

Существует также величина, обратная периоду, которая называется частотой. Эта величина равна числу оборотов в единицу времени. Очевидно, что период обращения и частота обратно пропорциональны:

К примеру, чем быстрее вращаются лопасти вентилятора, тем больше он оборотов совершит в единицу времени и тем меньше период обращения.

Еще одной важной характеристикой движения по окружности является угловая скорость. Скорость, о которой мы говорили до этого — это фактическая скорость движения, которая называется линейной.

Угловая скорость характеризует скорость поворота, то есть изменение угла поворота в единицу времени.

Таким образом, угловая скорость измеряется в радианах в секунду:

.

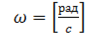
Напомним, что радиан — это угол между двумя радиусами окружности, вырезающими на окружности дугу, длина которой равна радиусу окружности. Применительно к физике, мы можем сказать, что радиан — это такой угол, при повороте на который, точка проходит путь, равный радиусу окружности.

Мы знаем, что полный оборот — это поворот на угол, равный 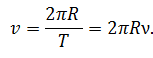. Тогда, угловая скорость будет равна:

Линейная скорость будет определяться:

Также можно записать, что линейная скорость равна произведению угловой скорости и радиуса окружности:

Это вполне логично: чем дальше точка находится от центра, вокруг которого она вращается, тем больше должна быть её линейная скорость, чтобы за одинаковое время совершить поворот на одинаковый угол.

Мы рассмотрели частный случай: когда точка совершает полный оборот по окружности. В более общем случае, угловая скорость будет определяться как отношение угла поворота ко времени, за который этот поворот был совершён:

Аналогично, линейная скорость определяется как отношение длины пройденной дуги ко времени:

Для примера рассмотрим, так называемый, геостационарный спутник. Это искусственный спутник Земли, который постоянно находится над одной и той же точкой поверхности Земли (с помощью таких спутников работает спутниковое телевидение, к примеру). Для выполнения этого условия необходимо, чтобы спутник вращался с той же угловой скоростью, что и Земля.

Пример решения задачи.

Задача. Спидометр автомобиля показывает 90 км/ч, а тахометр — 2400 об/мин. Чему равен радиус колеса в таком случае?

Источник

Равномерное движение точки по окружности

Урок 7. Физика 10 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Равномерное движение точки по окружности»

Вы уже знаете, что прямолинейное движение, тем более равномерное, встречается гораздо реже, нежели движение по криволинейной траектории. Кто из вас не наблюдал, как вращается волчок? А кто не катался на каруселях? Наконец, всем вам известно, что спутники обращаются вокруг планет почти по круговым траекториям, а планеты — вокруг центрального тела нашей Солнечной системы.

Криволинейных траекторий существует бесчисленное множество. Но оказывается, что любую кривую мы можем представить в виде совокупностей дуг окружностей разных радиусов и прямолинейных участков. Поэтому чаще всего изучение криволинейного движения сводится к изучению движения точки по окружности.

Мы будем изучать самый простой вид такого движения — равномерное движение точки по окружности. При таком движении направления векторов скорости и ускорения непрерывно изменяются, но вот их модули остаются постоянным.

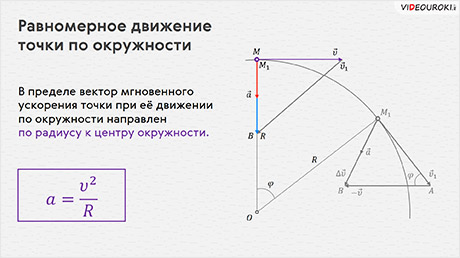
Итак, пусть материальная точка, равномерно движущаяся по окружности радиуса R, в некоторый момент времени t занимает положение М и имеет скорость υ, а спустя некоторый промежуток времени — положением М₁ и скорость υ₁. Найдём модуль и направление вектора ускорения точки в положении М.

Давайте найдём вектор изменения скорости за исследуемый промежуток времени:

Теперь давайте посмотрим на два треугольника ОММ₁ и М₁АВ. Что можно о них сказать? Во-первых, очевидно, что это два равнобедренных треугольника, так как ОМ и ОМ₁ — это радиусы окружности, а длины векторов скорости (их модули) одинаковы, так как движение точки у нас равномерное. Наконец, угол 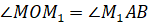как углы между двумя взаимно перпендикулярными сторонами. Следовательно, эти два треугольника подобны. Поэтому мы можем записать, что модуль изменения скорости точки так относится к модулю её скорости, как модуль перемещения к радиусу окружности, по которой эта точка движется:

Как мы уже с вами знаем, отношение модуля изменения скорости к промежутку времени, в течении которого это изменение произошло, — это модуль среднего ускорения точки. А отношение модуля перемещения к этому промежутку времени — это модуль средней скорости перемещения:

Теперь давайте с вами вспомним, что при стремлении промежутка времени к нулю отношение изменения скорости к промежутку времени, в течение которого это изменение произошло, называется ускорением. А отношение перемещения к промежутку времени называется мгновенной скоростью. Эти определения справедливы и для модулей скорости и ускорения:

После простых преобразований получим, что модуль ускорения точки при её движении по окружности прямо пропорционален квадрату модуля её скорости и обратно пропорционален радиусу окружности:

Учитывая, что при равномерном движении точки по окружности модуль её скорости и радиус окружности не меняются с течением времени, то и модуль вектора ускорения всё время остаётся неизменным. Но вот его направление, как и направление вектора скорости, меняется от точки к точке.

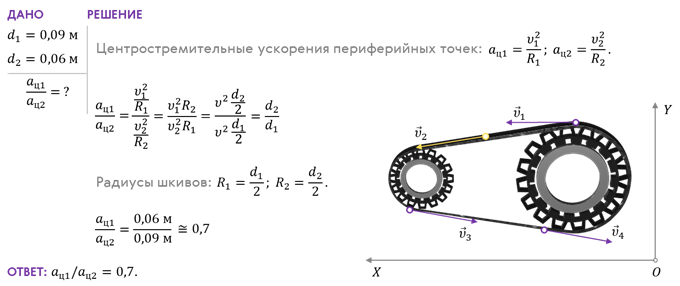
Задача 1. В ремённой передаче диаметр ведущего шкива равен 6 см, а ведомого — 9 см. Сравните центростремительные ускорения периферийных точек каждого шкива.

В заключение отметим, что равномерное движение точки по окружности является движением с переменной скоростью и переменным ускорением, так как направление их векторов непрерывно изменяется. Но их модули при этом остаются неизменными.

Источник