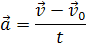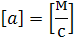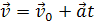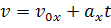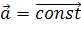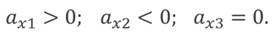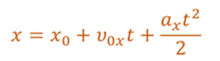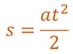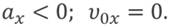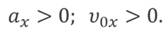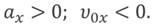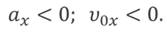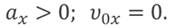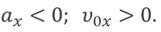Что такое равноускоренное ускорение
Ускорение при равноускоренном прямолинейном движении
теория по физике 🧲 кинематика
Ускорение тела равно отношению изменения вектора скорости ко времени, в течение которого это изменение произошло:
v — скорость тела в данный момент времени, v 0 — скорость тела в начальный момент времени, t — время, в течение которого изменялась скорость
Пример №1. Состав тронулся с места и через 20 секунд достиг скорости 36 км/ч. Найти ускорение его разгона.
Сначала согласуем единицы измерения. Для этого переведем скорость в м/с: умножим километры на 1000 и поделим на 3600 (столько секунд содержится в 1 часе). Получим 10 м/с.
Начальная скорость состава равно 0 м/с, так как изначально он стоял на месте. Имея все данные, можем подставить их в формулу и найти ускорение:
Проекция ускорения
vx — проекция скорости тела в данный момент времени, v0x — проекция скорости в начальный момент времени, t — время, в течение которого изменялась скорость
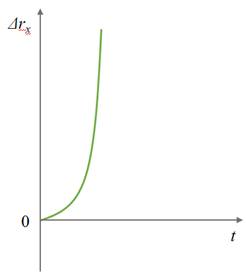
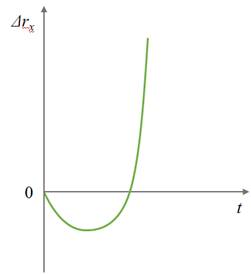
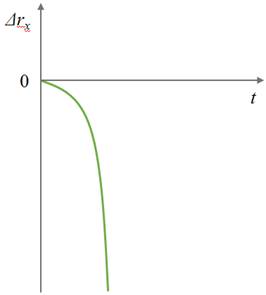
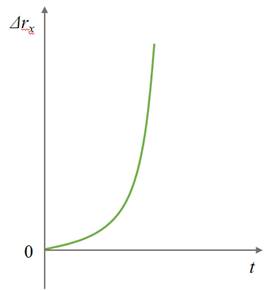
Знак проекции ускорения зависит от того, в какую сторону направлен вектор ускорения относительно оси ОХ:
При решении задач на тему равноускоренного прямолинейного движения проекции величин можно записывать без нижнего индекса, так как при движении по прямой тело изменяет положение относительно только одной оси (ОХ). Их обязательно нужно записывать, когда движение описывается относительно двух и более осей.
Направление вектора ускорения
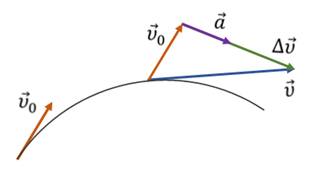
Направление вектора ускорения не всегда совпадает с направлением вектора скорости!
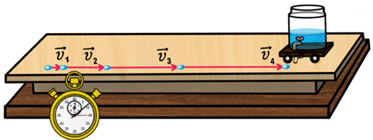
Равноускоренным движением называют такое движение, при котором скорость за одинаковые промежутки времени изменяется на одну и ту же величину. При этом направления векторов скорости и ускорения тела совпадают ( а ↑↑ v ).
Равнозамедленное движение — частный случай равноускоренного движения, при котором скорость за одинаковые промежутки времени уменьшается на одну и ту же величину. При этом направления векторов скорости и ускорения тела противоположны друг другу ( а ↑↓ v ).
Пример №2. Автомобиль сначала разогнался, а затем затормозил. Во время разгона направления векторов его скорости и ускорения совпадают, так как скорость увеличивается. Но при торможении скорость уменьшается, потому что вектор ускорения изменил свое направление в противоположную сторону.
График ускорения
График ускорения — график зависимости проекции ускорения от времени. Проекция ускорения при равноускоренном прямолинейном движении не изменяется (ax=const). Графиком ускорения при равноускоренном прямолинейном движении является прямая линия, параллельная оси времени.
Зависимость положения графика проекции ускорения относительно оси ОХ от направления вектора ускорения:
Если график ускорения лежит на оси времени, движение равномерное, так как ускорение равно 0. Скорость в этом случае — величина постоянная.
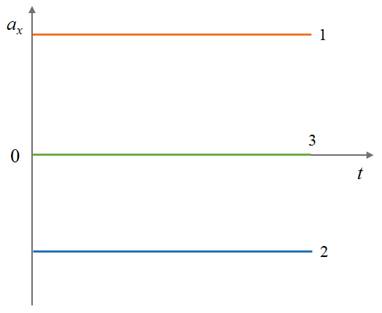
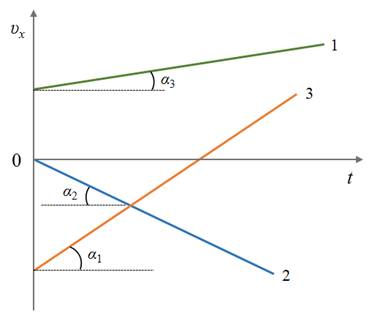
Чтобы сравнить модули ускорений по графикам, нужно сравнить степень их удаленности от оси времени независимо от того, лежат они выше или ниже нее. Чем дальше от оси находится график, тем больше его модуль. На рисунке график 2 находится дальше от оси времени по сравнению с графиком один. Поэтому модуль ускорения тела 2 больше модуля ускорения тела 1.
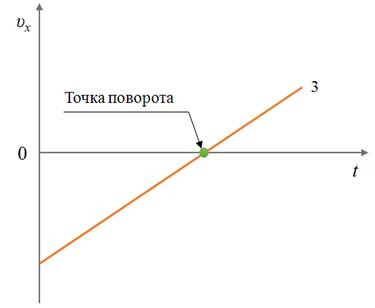
Пример №3. По графику проекции ускорения найти участок, на котором тело двигалось равноускорено. Определить ускорение в момент времени t1 = 1 и t2 = 3 с.
В промежуток времени от 0 до 1 секунды график ускорения рос, с 1 до 2 секунд — не менялся, а с 2 до 4 секунд — опускался. Так как при равноускоренном движении ускорение должно оставаться постоянным, ему соответствует второй участок (с 1 по 2 секунду).
Чтобы найти ускорение в момент времени t, нужно мысленно провести перпендикулярную прямую через точку, соответствующую времени t. От точки пересечения с графиком нужно мысленно провести перпендикуляр к оси проекции ускорения. Значение точки, в которой пересечется перпендикуляр с этой осью, покажет ускорение в момент времени t.
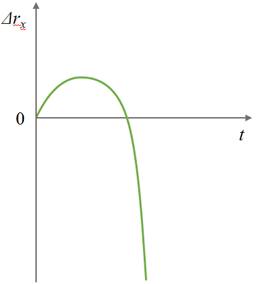
На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.
Алгоритм решения
Решение
График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:
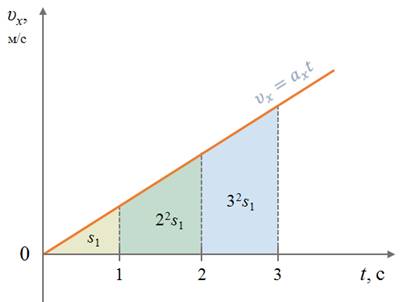
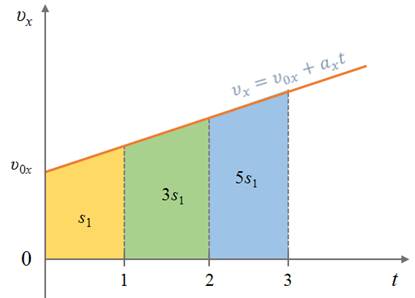
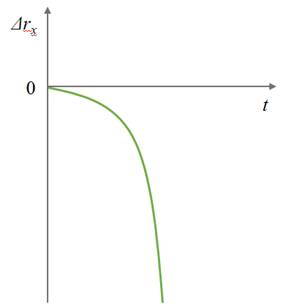
Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.
График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.
График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.
Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.
График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».
График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
Решение
Запишем исходные данные:
Формула, которая связывает ускорение тела с пройденным путем:
Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».
Выразим из формулы ускорение:
Подставим известные данные и вычислим ускорение автомобиля:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Внимательно прочитайте текст задани я и выберите верный ответ из списка. На рисунке приведён график зависимости проекции скорости тела vx от времени.
Какой из указанных ниже графиков совпадает с графиком зависимости от времени проекции ускорения этого тела ax в интервале времени от 6 с до 10 с?
Алгоритм решения
Решение
Согласно графику проекции скорости в интервале времени от 6 с до 10 с тело двигалось равнозамедленно. Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.
Чтобы выбрать между вариантами «б» и «г», нужно вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:
Используем для вычислений следующую формулу:
Подставим в нее известные данные и сделаем вычисления:
Этому значению соответствует график «г».
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
Решение
Записываем формулу ускорения:
По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий вид:
Выбираем любые 2 точки графика. Пусть это будут:
Подставляем данные формулу и вычисляем модуль ускорения:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Равномерное и равноускоренное движение
В процессе такого перемещения скорость тела периодически изменяется, поэтому для описания данного процесса применяют понятия средней и мгновенной скоростей.
Мгновенная скорость – это скорость движения тела, которая фиксируется в конкретный момент времени в заданной точке пути. Другими словами, мгновенной скоростью \(v\) есть предел стремления средней скорости тела \(v_<ср>\) при бесконечно малом промежутке времени:
Известно, что предел отношения приращения функции к приращению аргумента, в случае стремления последнего к нулю, – это главная производная функции по аргументу.
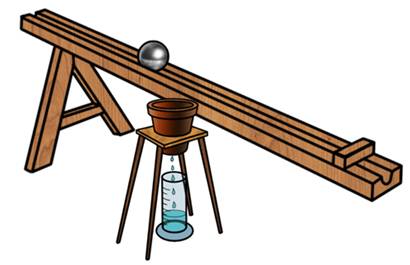
Рассмотрим пример скатывания шарика по наклонной поверхности. При этом мы наблюдаем, что шарик движется неравномерно: расстояния, которые он проходит за одинаковые последовательные интервалы времени, постоянно увеличиваются. То есть, темп его движения постоянно растёт. Данное движение, как и скачивание любого предмета, является классикой прямолинейного равноускоренного перемещения.
Еще одним примером такого движения является перемещение транспорта, когда он разгоняется, а так же когда тормозит. То есть равноускоренным движением может считаться не только ускоренное, но и замедленное движение.
Дело в том, что понятие «ускорение» в физическом смысле более широкое, нежели мы привыкли использовать в ежедневной жизни. Слово ускорение в широком потреблении понимается как увеличение скорости, но физически под ускорением понимается передвижение тела с постоянным изменением скорости, при этом неважно увеличивается она или уменьшается.
Сложно разобраться самому?
Попробуй обратиться за помощью к преподавателям
Понятие прямолинейного равноускоренного движения достаточно широко используется при изучении законов механики.
Стоит отметить, что при влиянии постоянной силы тело будет перемещаться равноускорено.
Равномерное движение
Равномерное движение – это такое механическое перемещение тела, когда за равные промежутки времени оно преодолевает равные расстояния.
Для равномерного перемещения характерно постоянное значение скорости:
где \(v\) – скорость равномерного перемещения, м/с;
\(l\) – расстояние, преодоленное объектом, м;
\(δt\) – промежуток времени перемещения, с.
При равномерном перемещении скорость предмета остаётся равной на каждом промежутке пути.
Если перемещение тела не только равномерное, а также прямолинейное, то его путь равен модулю его перемещения. Значит, аналогично предыдущему выражению, определяем скорость равномерного прямолинейного перемещения:
где \(\overline
\(\overline\) – перемещение тела, м;
\(δt\) – промежуток времени перемещения, с.
Скорость равномерного прямолинейного перемещения является векторной величиной. То есть её направление также имеет значение, как и модуль.
Равноускоренное движение тела
При равноускоренном перемещении скорость постоянно изменяется. Если речь идет об убыстрении, скорость постоянно растет. То есть ускорение остаётся величиной постоянной, а темп постоянно растет.
Помимо равноускоренного движения еще выделяют равнозамедленное, где темп постоянно уменьшается с одинаковой быстротой.
Различают одномерное и многомерное ускорение. Первое происходит вдоль одной оси координат, а второе – в плоскости или в пространстве.
Не нашли что искали?
Просто напиши и мы поможем
Ускорение тела
Формулы равномерного движения для расчета ускорения могут применяться без учёта времени в разных плоскостях. Например, при расчёте свободного падения жестких тел, можно определять их местоположение. Это бывает полезно при различных геометрических расчётах.
Неравномерное перемещение тела, так же как и равноускоренное, характеризуется изменением скорости. Но в чём же тогда их отличие? При равноускоренном – скорость тела не просто изменяется, она равно ускоряется.
Понятие ускорения часто ассоциируют с ростом скорости. Поскольку скорость растет одинаково, говорят о равном возрастании скорости. Как же определить, скорость растет равномерно или нет? Для этого засекают время, оценивают приращение скорости за равные промежутки времени, если при этом приращение одинаково на каждом новом участке, передвижение считается равноускоренным.
Ускорение – это физическая величина, показывающая на сколько возрастает скорость.
Замедленным движением есть перемещение с уменьшающейся скоростью. Поскольку в физике любое перемещение с меняющейся скоростью называется ускоренным, то неважно разгоняется автомобиль либо тормозит, в любом случае он передвигается с ускорением.
Значит, ускорение описывает быстроту изменения скорости. Оно показывает на сколько меняется скорость за одну секунду. Чем больше величина ускорения, тем стремительнее тело набирает скорость либо сбрасывает её. Ускорение обозначается буквой a и определяется соотношением изменения скорости δv к промежутку времени δt, за которое оно осуществлено:
Механическое движение
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Механическое движение
Когда мы идем в школу или на работу, автобус подъезжает к остановке или сладкий корги гуляет с хозяином, мы имеем дело с механическим движением.
Механическим движением называется изменение положения тел в пространстве относительно других тел с течением времени.
«Относительно других тел» — очень важные слова в этом определении. Для описания движения нам нужны:
В совокупности эти три параметра образуют систему отсчета.
В механике есть такой раздел — кинематика. Он отвечает на вопрос, как движется тело. Дальше мы с помощью кинематики опишем разные виды механического движения. Не переключайтесь 😉
Прямолинейное равномерное движение
Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.
Например, если у вас ограничение скорости на дороге 60 км/ч, и у вас нет никаких препятствий на пути — скорее всего, вы будете двигаться прямолинейно равномерно.
Мы можем охарактеризовать это движение следующими величинами.
Скалярные величины (определяются только значением)
Векторные величины (определяются значением и направлением)
Проецирование векторов
Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.
Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.
Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю.
Скорость может определяться по вектору перемещения и пути, только это будут две разные характеристики.
Скорость — это векторная физическая величина, которая характеризует быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.
Скорость
→ →
V = S/t
→
V — скорость [м/с]
→
S — перемещение [м]
t — время [с]
Средняя путевая скорость
V ср.путевая = S/t
V ср.путевая — средняя путевая скорость [м/с]
S — путь [м]
t — время [с]
Задача
Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.
Решение:
Возьмем формулу средней путевой скорости
V ср.путевая = S/t
Подставим значения:
V ср.путевая = 210/2,5 = 84 км/ч
Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч
Уравнение движения
Основной задачей механики является определение положения тела в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).
Уравнение движения
x(t) = x0 + vxt
x(t) — искомая координата [м]
x0 — начальная координата [м]
vx — скорость тела в данный момент времени [м/с]
t — момент времени [с]
Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v