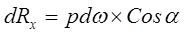Что такое равновесное состояние жидкости

РАВНОВЕСИЕ ЖИДКОСТИ

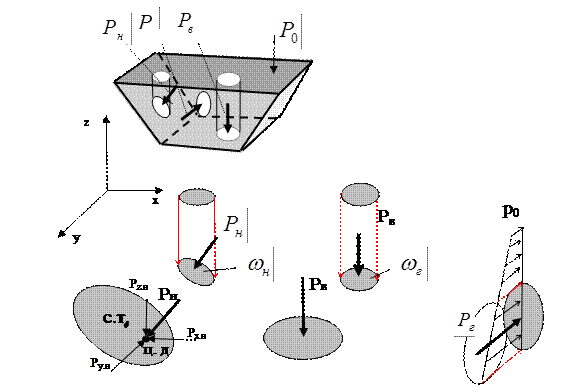
Действующие силы и равновесное состояние жидкости.Рассмотрим некоторый объем жидкости рис.2.2.1

Рассматриваемый объем жидкости находится в состоянии относительного равновесия. В этом случае выделенная точка М также находится в состоянии равновесия. Такое состояние предполагает равновесное состояние сил, воздействующих на выделенный объем.

Рис. 2.2.1.

На выделенный объем действуют внешние силы – поверхностные и объемные силы. Объемные силы – это внешние силы пропорциональные объему и плотности вещества. Поверхностные силы – силы, действующие в границах выделенного объема. Условие равновесия предполагает присутствие нормальной составляющей N и касательной составляющей K. Касательная составляющая К для условия относительного равновесия должна бать равна нулю. Таким образом, условие относительного равновесия в рассматриваемом случае предполагает равенство поверхностных и объемных сил.

Поверхностные силы. Поверхностные силы определяют так называемое поверхностное «напряжение». Поверхностное напряжение определяется выражением:

, (11)

Объемные силы. Объемные силы (массовые силы) определяются воздействие внешних сил. Для них можно записать:

(12)

Основная теорема гидростатики.Основная теорема гидростатики устанавливает то, что гидростатическое давление (р) в данной точке не зависит от его направления, т.е.:

, (13)

.где давления по направлению осей координат x,y,z и произвольному направлению i.

Рассмотрим некоторый элементарный объем жидкости (рис.2.2.2.) при условии, что он находится в состоянии равновесия.

В этом случае можно состояние равновесия выразить в виде трех уравнений проекций действующих сил и трех уравнений моментов:

и

и

и

При уменьшении граней выделенного объема в пределе до нуля система действующих сил превратится в систему сил, проходящих через точку, а система уравнений моментов теряет смысл.

Проекции этих сил на оси x, y, z можно представить в виде:

,

Где угол между нормальным направлением силы и соответствующей осью координат, а углы между составляющей равнодействующих массовых сил и осями координат.

;

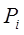
и .

Проводя подобные рассуждения, относительно проекций сил на другие оси координат, и осуществляя соответствующие преобразования, получим:

—

—

Или, проведя соответствующие преобразования окончательно, получим:

Учитывая, что последняя составляющая в данной системе уравнений, представляет величину высшего порядка малости, можем записать:

Что и требовалось доказать.

В данном случае было доказано равнозначность гидростатического давления в точке по любому направлению, однако не следует забывать, что давление является функцией координат и времени.

Основной закон гидростатики.Выделим в объеме некоторую элементарную площадку 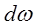. Данная площадка сверху нагружена столбом жидкости высотою , где высота столба жидкости (воздуха) над свободной поверхностью жидкости.

Рис.2.2.3.

Предполагая, что жидкость находится в состоянии относительного покоя. Выделим элементарный объем рис.2.2.3.

Условие равновесия выделенного элементарного объема предполагает равенство массовых и поверхностных сил. В проекциях на оси x, y, z можем записать:

(19)

(19 а)

Система уравнений (19 а) описывает относительное равновесное состояние жидкости (система уравнений равновесного состояния жидкости-Эйлера).

Сложение правых и левых частей уравнения позволяет получить уравнение:

(20)

Уравнение (20) представляет собой основное уравнение гидростатики.

Уравнение поверхности уровня. Поверхность уровня представляет поверхность равного давления. Поверхность уровня предполагает или

В этом случае уравнении (20) примет вид:

(21)

Уравнение (21) представляет уравнение поверхности уровня.

Поверхность уровня обладает определенными свойствами:

1. Поверхности уровня не пересекаются.

2. Направление объемных сил нормально к поверхности уровня.

Равновесие жидкости в поле земного тяготения.Рассматривая уравнение (20) для случая работы его в поле земного тяготения, т.е. X=0, Y=0, а Z=-g (см. рис. 2.2.3). В данном случае уравнение (20) примет вид

(22)

Проводя интегрирование уравнения (22) окончательно получим

(23)

Где величина гидростатического давления столба воздуха над выделенной поверхностью; -высота столба воздуха; — высота столба жидкости над выделенной поверхности.

Окончательно уравнение (23) примет вид:

(23 а)

Сила давления жидкости на плоские поверхности. Определим силу давления P_н на произвольную наклонную площадь (рис.2.2.3). В данном случае величина P_н определяется из соотношения:

, (24)

Проекции силы P_н на оси xyz можно определить из выражений:

(25)

Где углы пространственной ориентации силы P_н

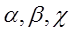
и осей координат xyz.

Центр давления. Центром давления называется точка приложения силы давления в столбе жидкости на расчетную площадку. Центр давления характеризуется координатами xyz, а для плоскости двумя координатами. В этом случае положение центра давления можно определить из выражения

, (26)

Где расстояние от поверхности уровня жидкости до точки приложения силы давления;

момент инерции площадки относительно рассматриваемой оси, проходящей через центр тяжести площадки;

расстояние от поверхности уровня жидкости до центра тяжести площадки;

угол ориентации площадки .

Для рассматриваемого случая, величина, т.е. центр давления всегда ниже центра тяжести рассматриваемой площадки. Исключение составляет частный случай, когда площадка, расположена горизонтально, в плоскости xoy. В этом случае центр давления совпадает с центром тяжести площадки. Расстояние между центром тяжести и центром давления принимается как эксцентриситетом приложения силы давления и центром тяжести.

Давление жидкости на криволинейные поверхности.Рассмотрим криволинейную поверхность (рис.2.2.4).

Так как поверхность пластины криволинейная, то силы dR образуют систему не параллельных сил. Такую систему можно привести к главному вектору R. В общем случае можем записать:

(27)

,

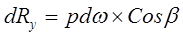
где 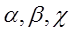углы пространственной ориентации силы R

и осей координат x y z.

Сумма проекций элементарных сил может быть выражена в виде равнодействующей силы R;

(28)

,

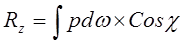
Сила R по величине будет рана;

, (29)

Решение уравнений (28) можно представить в виде:

(30)

,

где — глубина погружения центра тяжести площадок, соответственно .

Закон Архимеда. Погрузим тело произвольной формы (рис. 2.2.5) в жидкость. Определим величину сил воздействующих на рассматриваемое тело. На рассматриваемое тело действуют поверхностные и массовые силы. Проекции рассматриваемых сил приведены на рис. 2.2.5.

P_x, P_y, P_z –проекции поверхностных сил соответственно на оси координат x,y,z. Учитывая, что данная система находится поле сил земного тяготения, массовая сила, действующая на погруженное тело, составит

где h_н и h_в глубина погружения нижней и верхней граней тела, γ_т=ρg удельный вес погруженного тела, площадь грани нормальной к оси z.

В случае нахождения рассматриваемого тела в состоянии равновесия сумма поверхностных и массовых сил должна быть равна нулю.

, (32)

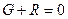
где G – сумма проекций массовых сил, R- сумма проекций поверхностных сил.

Подставляя в уравнение (32) составляющие получим

Из анализа уравнения (34) следует, что в случае равенства удельного веса тела и воды тело находится в состоянии покоя. При условии γ_в >γ_т тело должно всплыть, а при условии γ_в

Источник

Что такое равновесное состояние жидкости

Молекулярно-кинетическая теория позволяет не только понять, почему вещество может находиться в газообразном, жидком или твердом состояниях, но и объяснить процесс перехода вещества из одного состояния в другое. Фазой вещества называется термодинамически равновесное состояние вещества, отличающееся по физическим свойствам от других возможных равновесных состояний того же вещества. В однокомпонентной системе разные фазы могут быть представлены различными агрегатными состояниями или разными полиморфными модификациями вещества. В многокомпонентной системе фазы могут иметь различный состав и структуру. Переходы вещества из одного агрегатного состояния в другое, сопровождающееся изменением характера упаковки частиц системы, называются фазовыми переходами первого рода.

Из уравнения Ван-дер-Ваальса в применении к реальным газам следует, что при известных значениях температуры, давления и величин а и b газ образует систему из жидкости и газа (пара). До сих пор нет законченной теории жидкости, и потому мы рассмотрим систему жидкость – пар только с точки зрения учения о физическом равновесии.

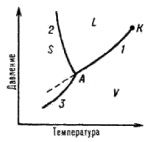
Рис. 1. Диаграмма состояния однокомпонентной системы

Двухфазное равновесие между жидкостью и паром изображается кривой кипения (или испарения) 1, между жидкостью и кристаллами – кривой плавления 2, между кристаллами и паром – кривой возгонки (или сублимации) 3. Здесь S, L и V – соответственно области существования твердой, жидкой и паровой фаз; К – критическая точка; А – тройная точка. Все двухфазные равновесия моновариантны, т.е. не нарушаются при произвольном изменении только одного из параметров, Т или р.

На практике при изучении равновесного состояния жидкость-пар на примере системы: уксусная кислота–диацетат–α–пропиленгликоль были получены следующие данные:

Источник

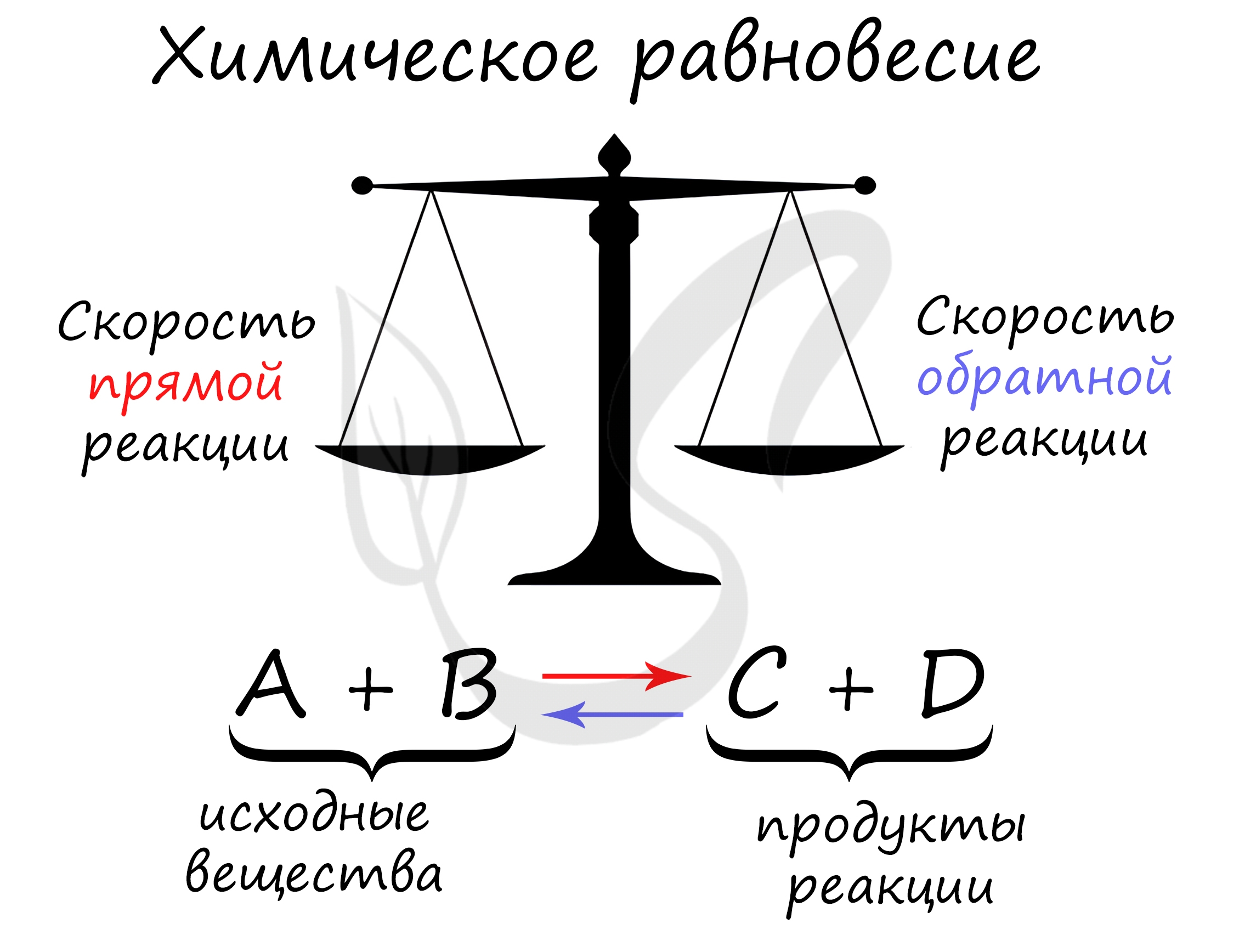
Химическое равновесие

Принцип Ле Шателье

В 1884 году французским химиком Анри Ле Шателье был предложен принцип, согласно которому, если на систему, находящуюся в состоянии равновесия, оказать внешнее воздействие (изменить температуру, давление, концентрацию), то система будет стремиться компенсировать внешнее воздействие.

Это принцип обоснован термодинамически и доказан. Однако в такой абстрактной формулировке его сложно применить для решения конкретных задач по химическому равновесию. В этой статье я покажу конкретные примеры и обозначу алгоритм действия, чтобы вы могли успешно справляться с заданиями.

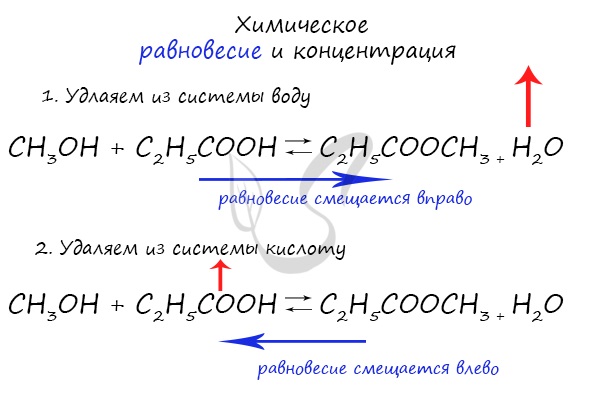
Влияние изменения концентрации на химическое равновесие

При увеличении концентрации какого-либо компонента химической реакции, система будет стремиться восстановить равновесие: равновесие будет смещаться в сторону расходования добавленного компонента.

Если мы попытаемся удалить какое-либо вещество из системы (уменьшить его концентрацию), то система будет стремиться заполнить «пустое» место, которые мы создали. Наглядно демонстрирую на примере:

Изменения давления и химическое равновесие

Если речь в задании идет об изменении давления, то первое, что нужно сделать, это посчитать количество газов в уравнении слева и справа. Твердые вещества и жидкости считать не нужно. Например:

В случае, если слева и справа количество молекул газа одинаково, например, в реакции:

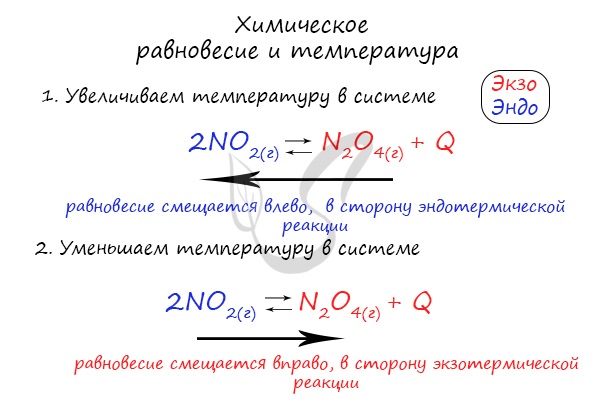
Изменение температуры и химическое равновесие

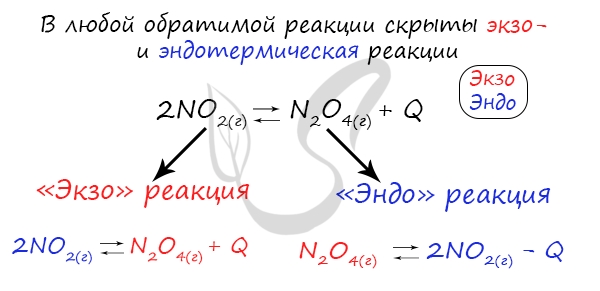
Если в задании увеличивают или уменьшают температуру, то первое, что вы должны оценить: экзотермическая это реакция или эндотермическая.

Поэтому данное правило универсально и применимо для всех реакций. Для примера разберем следующие задачи:

Чтобы не осталось белых пятен, возьмем экзотермическую реакцию и повторим с ней подобный эксперимент.

Катализатор и ингибитор

Действие катализатора и ингибитора соответственно касается только ускорения и замедления химической реакции. Они никоим образом не влияют на равновесие.

Константа равновесия

Константой равновесия называют отношения скоростей прямой и обратной реакции. Для реакции типа aA + bB = cC + dD константа равновесия будет записана следующим образом:

© Беллевич Юрий Сергеевич 2018-2021

Данная статья написана Беллевичем Юрием Сергеевичем и является его интеллектуальной собственностью. Копирование, распространение (в том числе путем копирования на другие сайты и ресурсы в Интернете) или любое иное использование информации и объектов без предварительного согласия правообладателя преследуется по закону. Для получения материалов статьи и разрешения их использования, обратитесь, пожалуйста, к Беллевичу Юрию.

Источник