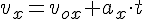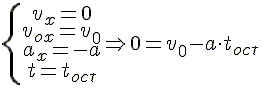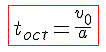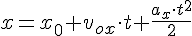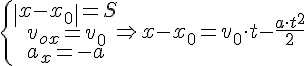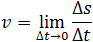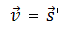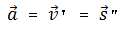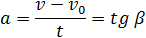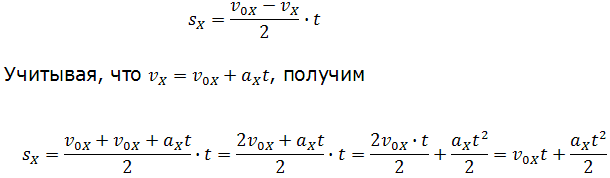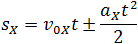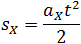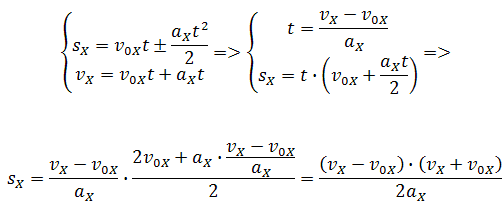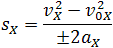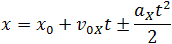Что такое равнозамедленное прямолинейное движение

Что такое равнозамедленное прямолинейное движение

§ 25. Равнозамедленное движение. Формула пути

1. Понятие равнозамедленного движения. Формула пути.

Это движение также является частным случаем движения с постоянным ускорением, поэтому любую задачу на это движение можно решать с помощью известных формул проекций скорости и координат движения с постоянным ускорением. Но иногда для более быстрого решения задач можно использовать формулы модуля скорости и пути.

Вначале найдём время, в течение которого тело движется равнозамедленно до остановки.

Получим теперь формулу модуля скорости равнозамедленного движения.

, где , то есть .

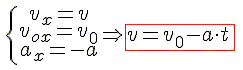
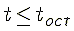
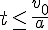
Из формулы координаты движения с постоянным ускорением можно получить формулу пути равнозамедленного движения.

, где .

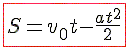
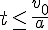
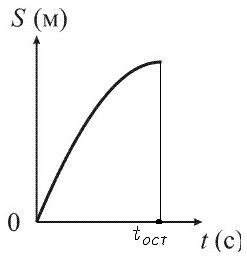
2. График пути равнозамедленного движения.

Графиком пути при равнозамедленном движении является ветвь параболы; вершина параболы расположена в конце времени движения.

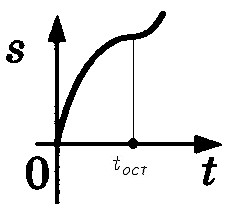
2а. Тело двигалось равнозамедленно, остановилось, а затем вновь начало двигаться (равноускоренно) в противоположном направлении: например, мяч, брошенный вертикально вверх.

График пути в этом случае будет выглядеть так.

Никакую часть этого материала ни в каких целях, включая образовательные и научные, нельзя без письменного разрешения владельца авторских прав дублировать в сети Интернет и воспроизводить в какой бы то ни было форме и какими бы то ни было средствами, будь то электронные или механические, включая запись на магнитный или электронный носитель, вывод на печать, фотокопирование.

Источник

Равнопеременное движение

Рассмотрим прямолинейное движение тела вдоль оси (одномерный случай) и пусть при этом скорость тела изменяется.

Когда скорость изменяется, появляется ускорение. Ускорение, в свою очередь, тоже может меняться.

Если изменяется и ускорение, и скорость тела – движение сложное, например, колебательное;

Движение равнопеременное — если изменяется только скорость, а ускорение постоянное.

Термин «равнопеременное» применяют потому, что за одинаковые интервалы времени перемещение изменяется на одну и ту же величину.

При этом, если скорость увеличивается – движение называют равноускоренным, а если скорость уменьшается – равнозамедленным.

Примечание: Вместо слов «ускорение постоянное» можно произнести «ускорение не меняется», или «ускорение одно и то же».

Рекомендую предварительно ознакомиться с основными терминами для описания движения.

Будем выбирать направления для векторов скорости и ускорения относительно оси. Разберем несколько возможных вариантов.

Равноускоренное движение

Пусть при движении по прямой скорость тела увеличивается. Обратим внимание на перемещение тела.

Примечание: Движение равноускоренное, значит, за одинаковые интервалы времени перемещение будет увеличиваться на одну и ту же величину.

Этот факт иллюстрирует рисунок 1. Из рисунка видно: по сравнению с первой секундой, за вторую секунду пути перемещение увеличивается на небольшой отрезок, а за третью секунду – на два таких отрезка.

Считаем, что векторы скорости и ускорения сонаправлены с осью, вдоль которой движется тело (рис. 2).

Примечание: Скорость увеличивается, когда вектор ускорения сонаправлен с вектором скорости.

В начальный и в конечный моменты времени скорости будут различаться.

Формулы можно записать в скалярном виде, так как движение происходит вдоль одной прямой и направления векторов известны.

Связь между начальной и конечной скоростью выглядит так:

Уравнение движения выглядит так:

\[ S = v_ <0>\cdot t + a \cdot \frac <2>\]

\[ x – x_ <0>= v_ <0>\cdot t + a \cdot \frac <2>\]

Кроме уравнения движения теперь есть связь между скоростями. Поэтому, решая задачи, в которых скорость увеличивается, используем систему, состоящую из двух таких уравнений:

\[ \large \boxed < \beginv = v_ <0>+ a \cdot t \\ S = v_ <0>\cdot t + a \cdot \frac <2>\end > \]

Примечание: Перемещение тела можно вычислить, не обладая информацией о времени движения, зная только начальную и конечную скорость тела и его ускорение. Об этом подробно написано в статье о формуле пути без времени.

Равнозамедленное движение

Пусть теперь тело движется по прямой и его скорость уменьшается. Рассмотрим перемещение тела.

Примечание: Движение равнозамедленное, значит, за одинаковые интервалы времени перемещение будет уменьшаться. При чем, на одну и ту же величину.

На рисунке 3 представлено изменение перемещения. Видно, что по сравнению с первой секундой, за вторую секунду перемещение уменьшается на небольшой отрезок, а за третью секунду – на два таких отрезка.

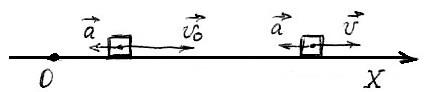
Примечание: Скорость будет уменьшаться, когда вектор ускорения направлен противоположно вектору скорости.

Пусть вектор скорости сонаправлен с осью, вдоль которой движется тело, а вектор ускорения – направлен против этой оси.

В начале и в конце пути скорости будут различаться.

Формулы можно записывать в скалярном виде, так как движение происходит вдоль одной прямой. Будем использовать знаки проекций векторов на ось.

Связь между скоростями выглядит так:

А уравнение движения имеет такой вид:

\[ S = v_ <0>\cdot t — a \cdot \frac <2>\]

Заменив перемещение разностью конечной и начальной координат \( S = x — x_<0>\), получим:

\[ x – x_ <0>= v_ <0>\cdot t — a \cdot \frac <2>\]

Значит, когда скорость уменьшается, для решения задач нужно использовать систему из двух таких уравнений:

\[ \large \boxed < \beginv = v_ <0>— a \cdot t \\ S = v_ <0>\cdot t — a \cdot \frac <2>\end > \]

Расшифруем теперь, к примеру, словосочетание «прямолинейное равнозамедленное движение» — это движение по прямой, ускорение есть, оно не меняется. Скорость тела уменьшается, так как вектор ускорения направлен противоположно вектору скорости.

Примечание: Перемещение замедляющегося тела можно вычислить не используя время. Потому, что существует запись формулы пути без времени для случая, когда скорость тела уменьшается.

Скорость направлена против оси, а ускорение – по оси

Дополнительно рассмотрим случай, когда скорость и ускорение направлены в противоположные стороны, ускорение – по оси, а скорость – против оси (рис. 5).

А если тело продолжит движение, то начнет двигаться в обратную сторону и модуль его скорости начнет увеличиваться. Поэтому, такое движение будет равноускоренным и будет сонаправленным с вектором ускорения.

Когда скорость направлена против оси, ее проекция на ось отрицательна и в уравнение она войдет со знаком минус. Ускорение же, напротив, совпадает с направлением оси, поэтому, войдет в уравнение со знаком «+».

Запишем связь между скоростями:

Уравнение движения для рассмотренного случая имеет такой вид:

\[ x – x_ <0>= — v_ <0>\cdot t + a \cdot \frac <2>\]

Для выбранного направления векторов в итоге получим такую систему уравнений:

\[ \large \boxed < \beginv = — v_ <0>+ a \cdot t \\ x – x_ <0>= — v_ <0>\cdot t + a \cdot \frac <2>\end > \]

Решая задачи на движение, иногда вычисляют мгновенную и среднюю скорости.

Термины «мгновенная скорость» и «средняя скорость» применяют для случаев, когда скорость изменяется – то есть, для неравномерного движения.

Мгновенная скорость

Мгновенная скорость – это скорость тела в какое-то мгновение. Когда скорость тела меняется, то в различные мгновения (моменты времени) скорости будут различаться.

Мгновенную скорость v вычисляют, вместо символа t подставляя в формулу интересующее нас время:

Знак ускорения зависит его направления.

Средняя скорость

Средняя скорость тела – скорость, с которой нужно двигаться равномерно, чтобы пройти тот же путь за то же время.

Другими словами, средняя скорость помогает понять, с какой постоянной скоростью могло бы двигаться тело, чтобы пройти весь пройденный путь за такое же время.

Примечания:

Формула для расчета средней скорости:

\( S_<\text<весь>>(\text<м>) \) ​– полный путь, пройденный телом;

\( t_<\text<полное>> \left( c \right)\) – время, за которое тело прошло весь путь.

Источник

Равнопеременное прямолинейное движение

Равномерное прямолинейное движение – это частный случай неравномерного движения.

Неравномерное движение – это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений.

Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.

Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).

Равнопеременное движение может быть равноускоренным или равнозамедленным.

Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.

Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.

В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.

Средняя скорость переменного движения определяется путём деления перемещения тела на время, в течение которого это перемещение было совершено. Единица измерения средней скорости – м/с.

Мгновенная скорость – это скорость тела (материальной точки) в данный момент времени или в данной точке траектории, то есть предел, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:

Вектор мгновенной скорости равнопеременного движения можно найти как первую производную от вектора перемещения по времени:

Проекция вектора скорости на ось ОХ:

это производная от координаты по времени (аналогично получают проекции вектора скорости на другие координатные оси).

Ускорение – это величина, которая определяет быстроту изменения скорости тела, то есть предел, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:

Вектор ускорения равнопеременного движения можно найти как первую производную от вектора скорости по времени или как вторую производную от вектора перемещения по времени:

Если тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой:

Знак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению. Аналогично записываются уравнения проекций вектора скорости на другие оси координат.

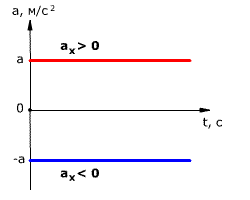
Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t (оси времени, рис. 1.15).

Рис. 1.15. Зависимость ускорения тела от времени.

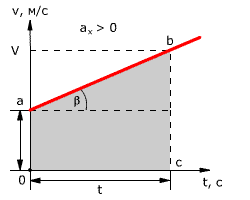
Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия (рис. 1.16).

Рис. 1.16. Зависимость скорости тела от времени.

График зависимости скорости от времени (рис. 1.16) показывает, что

При этом перемещение численно равно площади фигуры 0abc (рис. 1.16).

Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны:

Высота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна:

В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «–» (минус).

Общая формула для определения проекции перемещения:

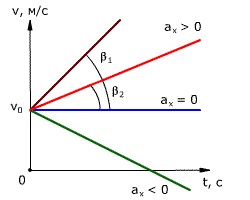
График зависимости скорости тела от времени при различных ускорениях показан на рис. 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.

Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения.

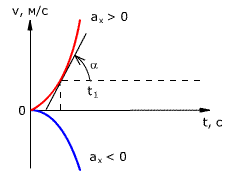
Рис. 1.18. Зависимость перемещения тела от времени.

Скорость тела в данный момент времени t₁ равна тангенсу угла наклона между касательной к графику и осью времени v = tg α, а перемещение определяют по формуле:

Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений:

Формула сокращённого умножения разности квадратов поможет нам вывести формулу для проекции перемещения:

Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, то уравнение движения тела будет выглядеть следующим образом:

Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат. При а_x

Источник

Перемещение и путь при равноускоренном прямолинейном движении

теория по физике 🧲 кинематика

Геометрический смысл перемещения заключается в том, что перемещение есть площадь фигуры, заключенной между графиком скорости, осью времени и прямыми, проведенными перпендикулярно к оси времени через точки, соответствующие времени начала и конца движения.

При равноускоренном прямолинейном движении перемещение определяется площадью трапеции, основаниями которой служат проекции начальной и конечной скорости тела, а ее боковыми сторонами — ось времени и график скорости соответственно. Поэтому перемещение (путь) можно вычислить по формуле:

Пример №1. По графику определить перемещение тела в момент времени t=3 с.

Перемещение есть площадь фигуры, ограниченной графиком скорости, осью времени и перпендикулярами, проведенными к ней. Поэтому в нашем случае:

Извлекаем из графика необходимые данные:

Подставляем известные данные в формулу:

Перемещение равно 0, так как тело сначала проделало некоторый путь, а затем вернулось в исходное положение.

Варианты записи формулы перемещения

Конечная скорость движения тела часто неизвестна. Поэтому при решении задач вместо нее обычно подставляют эту формулу:

В итоге получается формула:

Если движение равнозамедленное, в формуле используется знак «–». Если движение равноускоренное, оставляется знак «+».

Если начальная скорость равна 0 (v₀ = 0), эта формула принимает вид:

Если неизвестно время движения, но известно ускорение, начальная и конечная скорости, то перемещение можно вычислить по формуле:

Пример №2. Найти тормозной путь автомобиля, который начал тормозить при скорости 72 км/ч. Торможение до полной остановки заняло 3 секунды. Модуль ускорения при этом составил 2 м/с.

Перемещение при разгоне и торможении тела

Все перечисленные выше формулы работают, если направление вектора ускорения и вектора скорости совпадают ( а ↑↑ v ). Если векторы имеют противоположное направление ( а ↑↓ v ), движение следует описывать в два этапа:

Этап торможения

Время торможения равно разности полного времени движения и времени второго этапа:

Когда тело тормозит, через некоторое время t₁оно останавливается. Поэтому скорость в момент времени t₁ равна 0:

При торможении перемещение s₁ равно:

Этап разгона

Время разгона равно разности полного времени движения и времени первого этапа:

Тело начинает разгоняться сразу после преодоления нулевого значения скорости, которую можно считать начальной. Поэтому скорость в момент времени t₂ равна:

При разгоне перемещение s₂ равно:

При этом модуль перемещения в течение всего времени движения равен:

Полный путь (обозначим его l), пройденный телом за оба этапа, равен:

В данном случае движение нужно разделить на два этапа, так как мальчик сначала разогнался, потом затормозил. Тормозной путь будет соответствовать второму этапу. Через него мы выразим ускорение:

Из первого этапа (разгона) можно выразить конечную скорость, которая послужит для второго этапа начальной скоростью:

Подставляем выраженные величины в формулу:

Перемещение в n-ную секунду прямолинейного равноускоренного движения

Иногда в механике встречаются задачи, когда нужно найти перемещение тела за определенный промежуток времени при условии, что тело начинало движение из состояния покоя. В таком случае перемещение определяется формулой:

За первую секунду тело переместится на расстояние, равное:

За вторую секунду тело переместится на расстояние, равное разности перемещения за 2 секунды и перемещения за 1 секунду:

За третью секунду тело переместится на расстояние, равное разности перемещения за 3 секунды и перемещения за 2 секунды:

Видно, что за каждую секунду тело проходит перемещение, кратное целому нечетному числу:

Из формул перемещений за 1, 2 и 3 секунду можно выявить закономерность: перемещение за n-ную секунду равно половине произведения модуля ускорения на (2n–1), где n — секунда, за которую мы ищем перемещение тела. Математически это записывается так:

Формула перемещения за n-ную секунду

Пример №4. Автомобиль разгоняется с ускорением 3 м/с 2. Найти его перемещение за 6 секунду.

Подставляем известные данные в формулу и получаем:

Таким же способом можно найти перемещение не за 1 секунду, а за некоторый промежуток времени: за 2, 3, 4 секунды и т. д. В этом случае используется формула:

где t — время одного промежутка, а n — порядковый номер этого промежутка.

Время от 4 до 6 секунд включительно — это 3 секунды: 4-ая, 5-ая и 6-ая. Значит, промежуток времени составляет 3 секунды. До наступления этого промежутка успело пройти еще 3 секунды. Значит, время от 4 до 6 секунд — это второй по счету временной промежуток.

Подставляем известные данные в формулу:

Проекция и график перемещения

Проекция перемещения на ось ОХ. График перемещения — это график зависимости перемещения от времени. Графиком перемещения при равноускоренном движении является ветка параболы. График перемещения при равноускоренном движении, когда вектор скорости направлен в сторону оси ОХ ( v ↑↑OX), а вектора скорости и ускорения сонаправлены ( v ↑↑ a ), принимает следующий вид:

График перемещения при равнозамедленном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения противоположно ( v ↓↑ a ), принимает следующий вид:

Определение направления знака проекции ускорения по графику его перемещения:

Пример №6. Определить ускорение тела по графику его перемещения.

Перемещение тела в момент времени t=0 с соответствует нулю. Значит, ускорение можно выразить из формулы перемещения без начального ускорения. Получим:

Теперь возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 с. Этой точке соответствует перемещение 30 м. Подставляем известные данные в формулу и получаем:

График пути

График пути от времени в случае равноускоренного движения совпадает с графиком проекции перемещения, так как s = l.

В случае с равнозамедленным движением график пути представляет собой линию, поделенную на 2 части:

Такой вид графика (возрастающий) объясняется тем, что путь не может уменьшаться — он либо не меняется (в состоянии покоя), либо растет независимо от того, в каком направлении, с какой скоростью и с каким ускорением движется тело.

Пример №7. По графику пути от времени, соответствующему равноускоренному прямолинейному движению, определить ускорение тела.

При равноускоренном прямолинейном движении графиком пути является ветвь параболы. Поэтому наш график — красный. График пути при равноускоренном прямолинейном движении также совпадает с графиком проекции его ускорения. Поэтому для вычисления ускорения мы можем использовать эту формулу:

Для расчета возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 c. Ей соответствует путь, равный 5 м. Значит, перемещение тоже равно 5 м. Подставляем известные данные в формулу:

Тело массой 200 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой х(t) = 10 + 5t – «>– 3t 2 (все величины выражены в СИ).

Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

Алгоритм решения

Решение

Из условия задачи известна только масса тела: m = 200 г = 0,2 кг.

Так как тело движется вдоль оси Ox, уравнение движения тела при прямолинейном равноускоренном движении имеет вид :

Теперь мы можем выделить кинематические характеристики движения тела:

Перемещение тела определяется формулой:

Начальная координата не учитывается, так как это расстояние было уже пройдено до начала отсчета времени. Поэтому перемещение равно:

Кинетическая энергия тела определяется формулой:

Скорость при прямолинейном равноускоренном движении равна:

v = v 0 + a t = 5 − 6 t

Поэтому кинетическая энергия тела равна:

Следовательно, правильная последовательность цифр в ответе будет: 34.

pазбирался: Алиса Никитина | обсудить разбор | оценить

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения

Решение

График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:

Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.

График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.

График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.

Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.

График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».

График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».

pазбирался: Алиса Никитина | обсудить разбор | оценить

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Весь график можно поделить на 3 участка:

По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t₁ = 20 c до t₂ = 50 с. Этому времени соответствуют два участка:

Записываем формулу искомой величины:

s₁ — путь тела, пройденный на первом участке, s₂ — путь тела, пройденный на втором участке.

s₁и s₂ можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:

Теперь рассчитаем пути s₁и s₂, а затем сложим их:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник