Что такое равные отрезки
Отрезок
Отрезок — это часть прямой, ограниченная двумя точками, лежащими на этой прямой. Точки, определяющие границы отрезка, называются концами отрезка.
Отрезок обозначается двумя большими латинскими буквами, поставленными при его концах: отрезок AB или BA.
Длина отрезка
Длина отрезка — это расстояние между концами отрезка. Любой отрезок имеет длину, бо́льшую нуля:
Измерение длины отрезка осуществляется путём сравнения данного отрезка с длиной единичного отрезка. Единичный отрезок — это отрезок, длина которого принимается за единицу. Следовательно:
длина отрезка – это положительное число, показывающее, сколько раз единичный отрезок и его части укладываются в данном отрезке.
Чаще всего используются единичные отрезки равные 1 мм, 1 см, 1 дм, 1 м или 1 км. Измерить длину отрезка можно линейкой или любым другим прибором для измерения длины:
Свойства длин отрезков:
Равные отрезки
Равные отрезки — это отрезки, имеющие одинаковую длину. Если наложить равные отрезки друг на друга, то их концы совпадут.
Пример. Возьмём два отрезка CD и LM:
Если расположить отрезки параллельно друг над другом так, чтобы точка C была над точкой L, то станет видно, что точка D располагается над точкой М:
Значит длины отрезков равны, следовательно CD = LM.
Сравнение отрезков
Сравнить два отрезка — это значит определить, равны они, или один больше другого.
Сравнить два отрезка можно, отложив на прямой оба отрезка из одной точки в одну и туже сторону. Для этого можно воспользоваться циркулем.
Чтобы отложить на прямой отрезок равный данному, сначала помещают ножки циркуля так, чтобы острия их концов упирались в концы отрезка, а затем, не изменяя раствора циркуля, переносят его так, чтобы оба его конца находились на прямой.
При сравнении двух отрезков возможно получение одного из представленных результатов: отрезки будут равны, первый отрезок будет больше второго или первый отрезок будет меньше второго.
Пример. Если отложить на прямой от любой точки, например C, в одну сторону два отрезка CA и CB и точка A окажется между точками C и B, то отрезок CA меньше отрезка CB (или CB больше отрезка CA):
Если точка B окажется между точками C и A, то отрезок CA больше отрезка CB (или CB меньше отрезка CA):
CA > CB или CB Пример. Сравнить длину отрезков AB и AC.
Так как отрезок AB имеет большую длину, чем отрезок AC, то
Так как отрезки AB и AC имеют одинаковую длину, то
Если при измерении отрезков их длины равны, то и отрезки равны.
Середина отрезка
Середина отрезка — это точка, делящая отрезок на две равные части.
Математика. 5 класс
Конспект урока
Перечень рассматриваемых вопросов:
— понятие длины отрезка;
— равные отрезки на чертежах;
— определение длины отрезков.
Длина отрезка – число, которое показывает, сколько раз в отрезке содержится единичный отрезок.
Единичный отрезок – это отрезок, длина которого принята за единицу измерения.
Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др.– М.: Просвещение, 2017. – 272 с.
1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. –М.: Просвещение, 2009. – 142с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95с.
Теоретический материал для самостоятельного изучения
Каждому человеку неоднократно приходилось что-то измерять: свой рост, длину прыжка, высоту потолка и многое другое. Все эти действия означают вычисление величины какого-нибудь отрезка. Каким же образом можно измерить длину отрезка? На этот вопрос ответим в ходе урока.
За свою историю человечество придумало много разных единиц длины. Позже появились меры, заимствованные из природы:
— пядь – расстояние между растянутыми большим и указательным пальцами;
— вершок – длина основной фаланги указательного пальца;
— локоть – расстояние от локтевого сустава до конца вытянутого среднего пальца руки.
Некоторые названия сохранились до сих пор: ярд, фут, пядь, дюйм.
Ну, а герои одного известного мультфильма измеряли длину удава в попугаях. В зависимости от того, в ком измеряли удава, он становился то длиннее, то короче.
Два слонёнка, пять мартышек или тридцать восемь попугаев.
«А в попугаях я гораздо длиннее!» – воскликнул удав.
На самом деле мы с вами понимаем, что его размеры не менялись. Тогда возникает вопрос: в чём измерять? Что брать за единицу длины? Слонёнка, попугая или мартышку.
Измерить длину какого-нибудь отрезка в заданных единицах измерения – значит найти число, показывающее, сколько единичных отрезков поместится в данном отрезке.
Длиной отрезка называют число, которое показывает, сколько раз в отрезке содержится единица измерения.
Отрезок, длина которого принята за единицу измерения, называется единичным отрезком.
Чем же можно измерить длину отрезка?
Наиболее древними геометрическими инструментами являются линейка и циркуль, последний был изобретён в первом веке в Древней Греции.
Для более точных измерений используют миллиметровую линейку и штангенциркуль.
Далее построим отрезок ВК заданной длины –например, 8см. Для этого отметим точку В и приложим к ней линейку, совместив точку В с нулём. Затем отмеряем с помощью линейки 8 см, отмечаем точку К и соединяем обе точки линией.
Такой отрезок можно построить и с помощью циркуля. Для этого отметим точку В. Приложим к линейке циркуль, выставив его ножки на восемь сантиметров. Перенесём циркуль к точке В, поместив на неё одну ножку, а другой ножкой поставим точку К. Соединив обе точки линией, получим отрезок с длиной 8 см.
Отрезки можно сравнить с помощью измерителя –например, циркуля. Для этого попеременно подставляем ножки циркуля ко всем предложенным для сравнения отрезкам. При этом они должны быть выставлены по одному из отрезков. Если длины отрезков одинаковы, то отрезки считают равными и пишут CD = КМ.
Если один из отрезков является частью другого, следовательно, он короче. Например, ЕН короче EF, так как отрезок EH является частью EF.
Рассмотрим ещё одно свойство длин.
Если на отрезке АВ отметить точку С, то длина отрезка АВ равна сумме длин отрезков АС и СВ. Пишут: АВ = АС + СВ.
Наши органы чувств – это один из способов получения информации об окружающем нас мире, но информация полученная таким образом, бывает искажена.
Посмотрите на рисунки и ответьте на вопрос, равны ли отрезки?
На первый взгляд покажется, что правый отрезок больше, чем левый, но при сравнении с помощью линейки окажется, что отрезки равны.
Такая же ситуация, складывается и со следующей картинкой. Кажется, что нижний отрезок больше, чем верхний, но при наложении линейки окажется, что отрезки равны.
В другом же случае на тот же вопрос о равенстве отрезков ответ очевиден.
Таким образом, можно сделать вывод, что глазомерные оценки геометрических реальных величин неточны.
Разбор решения заданий тренировочного модуля
№1. Тип задания: выбор элемента из выпадающего списка.
Сравните длины горизонтального и вертикального отрезков?
Правильный ответ: при выполнении данного задания нужно использовать линейку, нужно измерить длину каждого отрезка и сравнить их. В результате измерений мы увидим, что отрезки равны.
№2. Тип задания: выделение цветом.
Точка К расположена на прямой между точками А и В. Длина отрезка АК = 8 см, длина отрезка КВ на 2 см больше длины отрезка АК. Какова длина отрезка АВ?
Выберите правильный ответ: 6 см; 10 см; 12 см; 18 см.
Решение: изобразим условие задачи на рисунке.
Шкалы, координаты
Для определения размера какой-либо величины (длина, вес, температура и т.д.) мы используем измерительные приборы и инструменты со шкалами для отображения результата.
Шкала – это расположенный в определенной последовательности ряд отметок, которые соответствуют числовому значению измеряемой величины.
Например, в школьном курсе математики и геометрии для измерения длины геометрического объекта, в частности отрезка, используется линейка (рисунок 1).
Рисунок 1. Измерительная линейка.
Из урока Измерение величин вы уже знаете, что такое единица измерения, а их соотношения можете посмотреть в справочном разделе.
Деления шкалы – это равные части, на которые она разбита. Каждое деление шкалы обозначается отметками (черточками).
Нулевая отметка шкалы – это отметка, которая соответствует нулевому значению измеряемой нами величины.
Цена деления шкалы – это величина значения одного деления шкалы. То есть, это величина значения между двумя соседними отметками на шкале.
Как мы видим на рисунке 1, деления, обозначенные большими черточками, пронумерованы, и значение каждого такого деления равно 1 см. В этом легко убедиться, если найти разницу между значениями каждого из соседних делений: 1-0=1, 2-1=3, …, 9-8=1, 10-9=1.
Но каждое из больших делений разделено девятью маленькими черточками на 10 делений. Мы знаем, что в 1 см содержится 10 мм, поэтому разделив эти 10 мм на 10 делений, мы получим цену деления линейки, равную 1 мм.
Цена деления может отличаться не только у разных же измерительных приборов, но и у одних и тех же.
Рисунок 2 Цена деления шкалы
Например, на рисунке 2 изображены два термометра. Как вы думаете, они показывают одинаковую температуру, или нет?
Давайте посмотрим, так ли это? На левом термометре разница между двумя соседними пронумерованными отметками равна 10°C: 10-0=10, 20-10=10, и т.д. На правом же термометре эта разница равняется уже 20°C: 20-0=20, 40-20=20, и т.д. На обоих термометрах маленькие черточки делят одно большое пронумерованное деление на 10 частей. Разделив разницу между значениями пронумерованных отметок (10 и 20 соответственно) на количество делений между ними (10), мы получим цену деления каждого из термометров:
Итак, оба термометра показывают 20°C и еще два деления. Но на левом термометре это означает 20°C и еще два раза по 1°C, то есть, 20+2=22°C, а на правом – 20°C и еще два раза по 2°C, то есть, 20+4=24°C.
Координатный луч, единичный отрезок, координаты точки
Различные прямые линии со шкалами играют важную роль в школьной математике. Сейчас я познакомлю вас с одной из них.
Нарисуем точку O и проведем от нее направо луч. Обозначим направление луча стрелкой.
Рис. 3. Луч с началом в точке O
Рис. 4. Луч с равными отрезками
Поставим возле начала луча (точки O ) число 0 (нуль). Возле второго конца отрезка OP (возле точки P ) поставим число 1 (один). Таким образом мы обозначаем, что длина отрезка OP равна 1 (единице).
Аналогичным образом вы можете легко найти числа, соответствующей каждой поставленной нами на луче точке.
Рис. 5. Луч с отрезками и цифрами
Покажу еще раз на примере точки S :
так как RS=OP (по условиям построения данных отрезков),
подставив известные нам значения длины отрезков OR и OP, получим:
Значит, точке S на нашем лучу соответствует число 3.
Оставим на луче только числовые значения, а все буквы кроме O отбросим. В итоге у нас получился вот такой луч с отрезками и числами, которые соответствуют концам этих отрезков.
Рис. 6. Координатный луч
Глядя на рисунок 6, легко заметить, что отрезки, лежащие на луче, это не что иное, как нанесенная на луч шкала. Действительно, смотрите сами.
Точка O с соответствующим ей числом 0 (нуль) называется точка отсчета, что аналогично нулевой отметке шкалы. Обычно этой буквой всегда помечают в рисунках точку отсчета.
Единичный отрезок – это отрезок, длина которого принята нами за единицу длины и равна 1(единице). Точке, обозначающей правый конец единичного отрезка, соответствует число 1.
Координатный луч – это луч с отмеченным на нем единичным отрезком, точкой начала отсчета, которой соответствует число 0 (нуль), и указанным направлением отсчета.
Координатный луч еще называют числовой луч.
Координатный луч — это не что иное, как бесконечная шкала.
Длина единичного отрезка может быть любой. Она выбирается каждый раз отдельно и при ее выборе ориентируются на то, чтобы на рисунке поместились все необходимые в данный момент числа. Например, на рисунке 7-а длина единичного отрезка составляет 5 см, а на рисунке 7-б всего 1 см.
Рис. 7. Разные варианты единичного отрезка
Как вы заметили из предыдущего рисунка, для разметки луча отрезками можно вместо кружочков использовать штрихи везде, кроме точки O (начала отсчета). Кружочки рисуют поверх этих штрихов тогда, когда необходимо отметить на числовом луче какое-то натуральное число. В этом случае мы дополнительно обозначаем его заглавной (большой) буквой латинского алфавита (смотрите рисунок 8).
Координатный луч служит для наглядного отображения и сравнения чисел натурального ряда.
Действительно, длина каждого отрезка числового луча отличается от длины предыдущего на единицу, точно так же, как и каждый элемент числового ряда отличается от предыдущего.
Координата точки числового луча – это число, которое соответствует поставленной на числовом луче точке.
Рис. 8. Координаты точек
Точке A соответствует число 5 координатного луча, точке B – число 8, точке C – число 13. Запишем полученные координаты точек: A ( 5 ), B ( 8 ), C ( 13 ).
В отдельных случаях для обозначения на координатном луче больших натуральных чисел, допускается не отображать на рисунке точку отсчета и единичный отрезок, показывая только тот участок луча, на котором расположены данные числа.
Рис. 9. Большие числа на координатном луче.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.2 / 5. Количество оценок: 9
Сравнение отрезков. Действия над отрезками.
Равные и неравные отрезки
Пусть нам даны два отрезка АВ и СD (рис.). Наложим отрезок АВ на отрезок CD так, чтобы точка А совпала с точкой С, и отрезок АВ направим по отрезку CD. Если точка В совпадаете точкой D, то отрезки АВ и CD равны; АВ = CD.
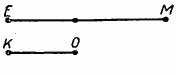
Сравним два отрезка КО и ЕМ (рис.).
Наложим отрезок КО на отрезок ЕМ так, чтобы точки К и Е совпали. Отрезок КО направим по отрезку ЕМ. Если точка О окажется где-нибудь между точками Е и М, то говорят, что отрезок ЕМ больше отрезка КО; отрезок КО меньше отрезка ЕМ.
Записывается это тaк: ЕМ > КО, КО 1 /5 часть отрезка МN.
в) Чтобы разделить отрезок на равные части с помощью циркуля, поступают таким образом. Например, если нужно разделить отрезок на две равные части, то циркуль раздвигают на глаз так, чтобы раствор циркуля составлял примерно половину отрезка. Затем на данном отрезке от его конца последовательно один за другим откладывают этим раствором циркуля два отрезка. Если полученная сумма отрезков будет меньше данного отрезка, тo раствор циркуля увеличивают; если сумма окажется больше данного отрезка, то раствор циркуля уменьшают. Так, постепенно исправляя ошибку, можно отыскать довольно точнo половину отрезка (рис.).
Свойство отрезков, отсекаемых параллельными прямыми на сторонах угла
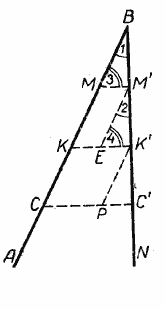
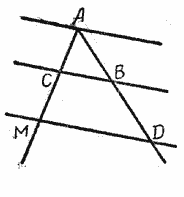
Пусть на стороне АВ угла АВN отложены равные отрезки ВМ = МК = КС (рис.) и через точки деления М, К и С проведены параллельные прямые, пересекающие сторону ВN того же угла.
На этой стороне образовались три отрезка: ВМ’, М’К’ и К’С’. Требуется доказать, что ВМ’ = М’К’ = К’С’.
Для доказательства через точки М’ и К’ проведём прямые, параллельные АВ. Мы получим треугольники ВММ’, М’ЕК’ и К’РС’. Сравним эти треугольники.
Сначала сравним треугольники МВМ’ и М’ЕК’. В этих треугольниках имеем:
∠1 = ∠2, как соответственные углы при параллельных ВА и М’Е и секущей ВN;
∠3 = ∠4, как острые углы 1 с соответственно параллельными сторонами (АВ || М’Е и ММ’ || КК’).
ВМ = МК по построению;
МК = М’Е, как противоположные стороны параллелограмма.
Углы 1-й и 4-й могут оказаться оба тупыми, но и в этом случае они останутся равными, а потому доказательство теоремы не изменится.
Следовательно, ВМ = М’Е. Таким образом, ΔВММ’ = ΔМ’ЕК’ (по стороне и двум прилежащим к ней углам). Отсюда следует, что ВМ’ = М’К’.
Так же можно доказать, что ВМ’ = К’С’, т. е. ВМ’ = М’К’ = К’С’. При доказательстве теоремы мы откладывание отрезков начали от вершины угла, но теорема справедлива и для того случая, когда откладывание отрезков будет начато не от вершины угла, а от любой точки его стороны.
В этом случае вершину угла на чертеже можно не отмечать (рис.).
Теорема справедлива и для случая, когда прямые КО и МР параллельны.
Пропорциональные отрезки
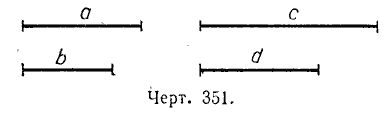
Из арифметики известно, что равенство двух отношений называется пропорцией. Например: 16 /4 = 20 /5; 2 /3 = 4 /6 To же самое имеем и в геометрии: если даны две пары отрезков, отношения которых равны, то можно составить пропорцию.
отрезки а, b, c, d называются пропорциональными.
В пропорции можно поменять местами отношения; можно переставить крайние члены, средние члены; можно переставить те и другие одновременно.
Поскольку в пропорции a /b = c /d под буквами подразумевают числа, выражающие длины отрезков, то произведение крайних членов её равно произведению средних членов. Отсюда, зная три члена пропорции, можно найти неизвестный четвёртый её член. Так, в пропорции a /x = c /d x = a • d /c
Отметим ещё некоторые свойства пропорций, которыми придётся в дальнейшем пользоваться при доказательстве некоторых теорем и при решении задач.
а) Если три члена одной пропорции соответственно равны трём членам другой пропорции, то равны и четвёртые члены этих пропорций.
Чтобы убедиться в этом, переставим средние члены в этой пропорции.
А это возможно лишь в том случае, когда числитель и знаменатель дроби равны, т. е.
В справедливости этого свойства предлагается вам убедиться самостоятельно. Для этого проведите рассуждение, аналогичное предыдущему.
Построение пропорциональных отрезков
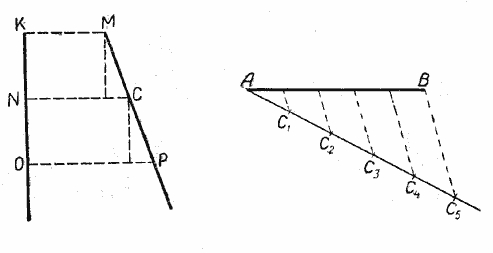
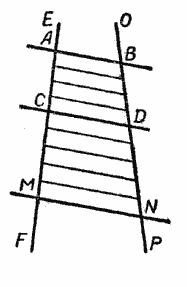
Пусть две прямые ЕF и ОР пересечены тремя параллельными прямыми АВ, СD и МN (рис.).
Требуется доказать, что отрезки АС, СМ, ВD и DN, заключённые между параллельными секущими, пропорциональны, т. е.
Пусть длина отрезка АС равна р, а длина отрезка СМ равна q.
Например, р = 4 см. и q = 5 см.
Разделим АС и СМ на отрезки, равные 1 см, и из точек деления проведём прямые, параллельные прямым АВ, СD и МN, как это показано на рисунке.
Тогда на прямой ОР отложатся равные между собой отрезки, при этом на отрезке BD их будет 4, а на отрезке DN — 5.
Значит, отрезки АС, СМ, ВD и DN пропорциональны. Пропорциональны также и отрезки АС, АМ, ВD и ВN (налегающие друг на друга), т. е. AC /AM = BD /BN,
Теорема будет справедлива и при любых других целых значениях р и q.
Если длины отрезков АС и СМ не выразятся в целых числах при данной единице измерения (например, сантиметре), то надо взять такую более мелкую единицу (например, миллиметр или микрон), при которой длины отрезков АС и СМ практически выразятся в целых числах.
Доказанная теорема справедлива и в том случае, когда одна из параллельных секущих проходит через точку пересечения данных прямых. Она справедлива также и в том случае, когда отрезки откладываются не непосредственно один за другим, а через некоторый промежуток.
Отрезок. Ломаная линия
Отрезок представляет собой часть прямой линии, которая находится между двумя точками. Эти точки называют концы отрезка.
Иными словами, отрезок – это множество точек прямой линии, находящиеся между двух известных точек, которые называют концами отрезка.
Рис. 1 Отрезок на прямой
Рис. 2 Несколько отрезков на прямой
Отрезок делит прямую линию на три объекта (смотри рисунок 3):
То есть, два конца отрезка прямой являются соответственно началами двух лучей этой же прямой.
Рис. 3 Отрезок и лучи прямой
Рис. 4 Отрезок без прямой
Рис. 5 Отрезок и принадлежащие ему точки
Так, на рисунке 5 видно, что:
В последнем случае точка F хотя и лежит на одной прямой линии с отрезком AB (если вы мысленно продлите линию от точки B дальше, то увидите это), но не принадлежит ему, потому что находится не между его концами, а справа от отрезка.
Рис. 6 Отрезок и части отрезка
Построение и измерение отрезка
Произвольный отрезок можно построить двумя способами:
Рис. 7 Построение произвольного отрезка
Измерить отрезок можно:
Сравнить отрезки между собой можно при помощи циркуля или циркуля-измерителя. Для этого нужно сперва поставить иглу на один конец отрезка, а затем вторую иглу или грифельный стержень (если используется обычный чертежный циркуль) совместить со вторым концом отрезка (рисунок 8).
Рис. 8 Сравнение отрезков
На рисунке 8 видно, что:
Длину отрезка измеряют линейкой с делениями или другим измерительным инструментом.
Длина отрезка – это расстояние между концами этого отрезка.
Равные отрезки — это такие отрезки, которые имеют одинаковую длину.
На рисунке 9 измерены длины отрезков предыдущего рисунка. Проверьте, правильно ли мы сравнили эти отрезки при помощи циркуля?
Рис. 9 Измерение длины отрезка
Для этого на плоскости обозначают один конец отрезка (ставят точку), а затем при помощи линейки отмеряют необходимую длину отрезка (к примеру, 9 см), ставят точку второго конца отрезка и соединяют оба конца линией.
Рис. 10 Построение отрезка заданной длины
Отрезок — это самое короткое расстояние между двумя точками.
В этом вы можете убедиться самостоятельно на практике. Возьмите любой твердый длинный предмет, например, линейку, и шнурок. Линейка будет играть роль отрезка, а из шнурка сделайте кривую и ломаную линию, наподобие таких, какие показаны на рисунке 11, и соедините ими два конца линейки. После чего выпрямите шнурок и сравните его длину с длиной линейки.
Рис. 11 Кривая, ломаная, отрезок
Ломаная линия
Ломаная линия – это линия, которая состоит из отрезков, принадлежащих разным прямым, и эти отрезки последовательно соединены друг с другом.
Рис. 12 Ломаная линия
На рисунке 12 видно, что:
Количество звеньев у ломаной линии может быть каким угодно, бесконечным, но самое меньшее – это два звена.
Замкнутая ломаная линия – это такая ломаная, у которой совпадают точки начала и конца, то есть, которая начинается и заканчивается в одной точке.
Разомкнутая (не замкнутая) ломаная линия начинается и заканчивается в разных точках.
Рис. 12. Замкнутая и разомкнутая ломаные линии
Самопересекающаяся ломаная линия – это такая ломаная, у которой есть хотя бы два пересекающихся звена.
Самопересекающимися могут быть как замкнутые, так и разомкнутые ломаные.
Рис. 13. Самопересекающиеся ломаные линии