Что такое разбиение в математике
Разбиение числа
Разбие́ние числа́ n — это представление n в виде суммы положительных целых чисел, называемых частями. При этом порядок следования частей не учитывается (в отличие от композиций), то есть разбиения, отличающиеся только порядком частей, считаются равными. В канонической записи разбиения части перечисляются в невозрастающем порядке.
Число разбиений 
Содержание
Примеры
Например, 









Некоторые значения числа разбиений 
Число разбиений
Производящая функция
Последовательность числа разбиений 
Эта формула была открыта Эйлером в 1740 году.
Пентагональная теорема Эйлера
Изучая производящую функцию последовательности 

Показатели степеней x в правой части — это пятиугольные числа, то есть, числа вида 


Согласно этому наблюдению Эйлер предположил, что должна быть верна Пентагональная теорема:

Впоследствии эта теорема была Эйлером доказана. Она позволяет вычислять числа разбиений при помощи деления формальных степенны́х рядов.
Асимптотические формулы
Асимптотическое выражение для количества разбиений было получено Харди и Рамануджаном и впоследствии уточнено Радемахером. Оригинальное выражение Харди — Рамануджана [источник не указан 48 дней]

дает, например, 
Здесь суммирование ведется по 


Рекуррентные формулы
Количество разбиений числа n на слагаемые, не превышающие k, удовлетворяет рекуррентной формуле:

с начальными значениями:



При этом количество всевозможных разбиений числа n равно 
Количество разбиений натурального числа n на k слагаемых удовлетворяет рекуррентной формуле:
с начальными значениями:


Конгруэнтности
Диаграммы Юнга
Разбиения удобно представлять в виде наглядных геометрических объектов, называемых диаграммами Юнга, в честь английского математика Альфреда Юнга. Диаграмма Юнга разбиения 




Более формально, диаграмма Юнга — это замыкание множества точек 

где 

В англоязычной литературе диаграммы Юнга часто изображают отражёнными относительно оси абсцисс.
Схожий объект, называемый диаграммой Ферре, отличается тем, что
Применение
Разбиения естественным образом возникают в ряде математических задач. Наиболее значимой из них является теория представлений симметрической группы, где разбиения естественно параметризуют все неприводимые представления. Суммы по всем разбиениям часто встречаются в математическом анализе.
См. также
Литература
Полезное
Смотреть что такое «Разбиение числа» в других словарях:
Разбиение — В математике Разбиение единицы Разбиение множества Разбиение интервала Разбиение числа … Википедия
Разбиение единицы — Разбиение единицы конструкция, используемая в топологии для удобства работы с многообразием как множеством карт. С помощью разбиения единицы определяется, в частности, интеграл от дифференциальной формы на многообразии. Конструкция Пусть… … Википедия
Разбиение графа — Пример разбиения параллельной граф схемы алгоритма логического управления. В составе блоков, отмеченных разными цветами, нет параллельных вершин Разбиение графа на подграфы (англ. Graph partition) (иногда в литературе также употребляется… … Википедия
Разбиение Аммония — Таблицы канонов Евсевия (окончание первого канона). Латинская рукопись Евангелий, V в. Апостольская библиотека, Ватикан (Vat. Lat. 3806. F° 2v.) Страница из Ватиканского кодекса 354, Евангелия от Луки (Лк 17:34 18:8), написанного поздним… … Википедия
Композиция числа — У этого термина существуют и другие значения, см. Композиция. Не следует путать с Композиция функций. В теории чисел композицией, или разложением, натурального числа называется его представление в виде упорядоченной суммы натуральных слагаемых.… … Википедия
Вещественные числа — Вещественные, или действительные[1] числа математическая абстракция, служащая, в частности, для представления и сравнения значений физических величин. Такое число может быть интуитивно представлено как описывающее положение точки на прямой.… … Википедия
Действительные числа — Вещественные, или действительные[1] числа математическая абстракция, служащая, в частности, для представления и сравнения значений физических величин. Такое число может быть интуитивно представлено как описывающее положение точки на прямой.… … Википедия
Реальные числа — Вещественные, или действительные[1] числа математическая абстракция, служащая, в частности, для представления и сравнения значений физических величин. Такое число может быть интуитивно представлено как описывающее положение точки на прямой.… … Википедия
КЛЕТОЧНОЕ РАЗБИЕНИЕ — CW комплекс, клеточный комплекс X, удовлетворяющий следующим условиям: (С) Для любой точки комплекс X(х)является конечным, т. е. состоит из конечного числа клеток (для произвольного подмножества А клеточного комплекса Xчерез X(А)обозначается… … Математическая энциклопедия
ЛОКАЛЬНОЕ РАЗБИЕНИЕ — свойство расположения замкнутого множества Ф в пространстве заключающееся в существовании такой точки а(точка, в к рой множество Ф разбивает пространство) и такого положительного числа что при любом числе в открытом множестве где (открытый) шар… … Математическая энциклопедия
Что такое разбиение в математике
Пусть p ( n ) обозначает количество всех разбиений натурального Для небольших n легко вычислить p ( n ), просто выписав все разбиения. Например, Вот все 7 разбиений (5), (4, 1), (3, 2), (3, 1, 1), (2, 2, 1), (2, 1, 1, 1), (1, 1, 1, 1, 1). Однако получить таким способом, скажем, без помощи компьютера немыслимо. Между было известно ещё в XIX веке. Мы познакомим вас со многими интересными свойствами разбиений и научим находить не выписывая всех разбиений
Задача вычисления p ( n ) имеет почтенный возраст. Впервые она была сформулирована Лейбницем в 1654 году, а в 1740 предложена немецким математиком Филиппом Ноде Леонарду Эйлеру. Занимаясь разбиениями, Эйлер открыл целый ряд их свойств, среди которых главное место занимала знаменитая «пентагональная теорема». С исследований Эйлера начинается история теории разбиений, в развитии которой принимали участие крупнейшие математики последующих поколений.
Две теоремы Эйлера
Изучение функции p ( n ) Эйлер начинает с рассмотрения бесконечного произведения
Каждый член произведения получается в результате умножения мономов, взятых по одному из каждой скобки. Если в первой скобке во то их произведение будет равно Значит, после раскрытия скобок получится сумма мономов вида
Посмотрим теперь на выражения в скобках. Каждое из них бесконечная геометрическая прогрессия. По формуле суммирования
и т.д. Теперь наш результат можно записать так:
Эта формула была открыта Эйлером в 1740 году. Ряд, стоящий в левой части, называется производящей функцией последовательности чисел Производящая функция позволяет компактно записать информацию о последовательности, хотя извлечение этой информации из производящей функции порой требует большого искусства. Сейчас вы увидите, как это делал Эйлер.
Обозначим через d ( n ) количество разбиений числа n на различные слагаемые, а через l ( n ) на нечётные. Например, среди выписанных выше разбиений различные части а нечётные и Значит,
Такие же рассуждения, как при выводе формулы (1), позволяют выписать производящие функции последовательностей
В правой части равенства все числители сокращаются со знаменателями, содержащими x в чётной степени. Поэтому в знаменателе останутся только сомножители вида Итак,
Значит, производящие функции последовательностей d ( n ) совпадают! Мы доказали теорему Эйлера : Это доказательство хорошо иллюстрирует силу метода производящих функций.
Но вернёмся к вычислению p ( n ). Изучая производящую функцию последовательности Эйлер сосредоточил внимание на произведении знаменателе правой части Раскрывая в нём скобки, Эйлер получил удивительный результат:
Пентагональная теорема оказалась «крепким орешком» Эйлер сумел доказать её лишь 14 лет спустя. Эта теорема позволяет сравнительно просто вычислять Вот как это делается.
и воспользуемся пентагональной теоремой:
Пользуясь формулой Эйлера, можно составить таблицу для что и проделал в начале известный английский специалист по комбинаторике майор В то время это была наиболее полная таблица
Итак, мы сформулировали две теоремы, одну из доказали. Согласитесь, что при всей элегантности этого доказательства, оно всё же оставляет чувство неудовлетворённости. Два множества разбиений на нечётные и на неравные части неожиданно оказались состоящими из одинакового числа элементов, но причина этого равенства осталась скрытой от нас. Хотелось бы думать, что существует естественный способ каждому элементу одного множества ставить в соответствие элемент другого.
Соответствия Глэйшера и Сильвестра
Приведём ещё два доказательства теоремы Эйлера:
Первое соответствие между разбиениями на различные слагаемые и разбиениями на нечётные слагаемые строится так:
Например, разбиению (6, 2, 1) соответствует разбиение (3, 3, 1, 1, 1). Это остроумное соответствие придумано в конце XIX века английским математиком Дж. Глэйшером.
Чтобы доказать взаимную однозначность соответствия Глэйшера, достаточно построить обратное соответствие между разбиениями с нечётными частями и разбиениями с неравными частями. Вот это соответствие:
Пусть в разбиении некоторая нечётная часть r встречается k раз. Запишем k в виде суммы различных степеней двойки
и заменим на То, что получится, будет разбиением с различными частями.
Например, разбиение (5, 5, 5, 1, 1, 1, 1, 1, 1) соответствует разбиению (10, 5, 4, 2), поскольку число пятёрок равно а число единиц равно
Существует другое, не менее интересное и совершенно неожиданное доказательство теоремы Эйлера, принадлежащее американскому математику XIX века Дж. Сильвестру. Вот конструкция Сильвестра: пусть имеется разбиение на нечётные части: где На листе клетчатой бумаги в некотором её узле поставим Справа поставим в узлах и столько же точек поставим в узлах, расположенных под Затем проделаем то же самое с взяв в качестве исходной расположенную в следующем за по диагонали направо вниз узле, пока не дойдём до
Например, разбиению на нечётные части (9, 9, 5, 1, 1) будет отвечать картинка, изображённая на рис. 1.
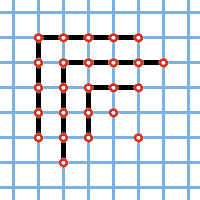 Рис. 1. | 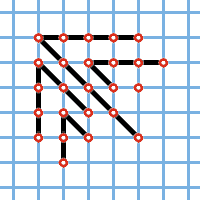 Рис. 2. |
В нашем примере получится разбиение (9, 6, 5, 4, 1). Подумайте, как построить по разбиению на различные части разбиение на нечётные, т.е. восстановить по такому разбиению исходную симметричную картинку.
Отступление: решение задачи М1065
В этом разделе используется более сложная техника, чем в остальной части статьи. При желании вы можете пробежать его, не вникая в детали, и продолжить чтение со следующего раздела. Итак, займёмся решением задачи М1065 из «Задачника «Кванта» Напомним её формулировку.
Решение задачи начнём с того, что найдём общий вид целочисленных решений неравенства Числа и имеют одинаковую чётность, поэтому является чётным при любых Следовательно, для любого достаточно найти целочисленные решения уравнения Положим Тогда Из этих двух равенств немедленно получаем:
где q любое целое число, а
Смысл чисел m и q станет более наглядным, если представлять себе векторы как точки с целыми координатами параболы лежащей в плоскости (Вы понимаете, почему это парабола?) Тогда полученные нами целочисленные решения неравенства показывают, что все точки с целыми координатами, лежащие на параболе и внутри неё, получаются сдвигами целых точек этой параболы на векторы (рис. 3). Удобно считать, что номер параболы, на которой лежит a номер точки на этой параболе.
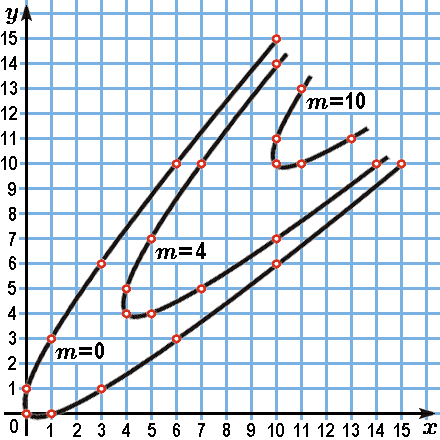
Рис. 3.
Поскольку условия задачи симметричны относительно перестановки координат векторов, достаточно доказать все утверждения для таких векторов что т.е. для векторов
Докажем достаточность условия в задачи. По формуле суммы арифметической прогрессии
Доказать необходимость условия тоже несложно. Пусть
Для такого вектора
(здесь мы снова воспользовались формулой суммы арифметической прогрессии). Из следует, что и вообще Поэтому вектор что и требовалось доказать.
В геометрических терминах означает, что зависит лишь от параболы и не зависит от точки на параболе.
Такую пару мы будем записывать в виде
Рассмотрим отображение φ множества в множество заданной формулой
Чтобы доказать, что φ взаимно однозначное отображение, построим обратное отображение прочитав правило, слева направо:
Построенные отображения взаимно обратны, поэтому φ взаимно однозначное соответствие. Значит, что и утверждалось.
Чтобы научиться вычислять значения установим связь между числами
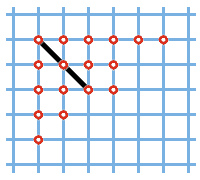
Рис. 4.
Проведём на диаграмме Юнга диагональ чёрная линия на рис. 4. Пусть точек в первой строке, лежащих на диагонали и справа от неё, точек второй строки, лежащих на диагонали и справа от неё, точек первого столбца под диагональю, точек второго столбца под диагональю Поставим в соответствие диаграмме Юнга, изображающей разбиение пару последовательностей
Теперь ничего не стоит ответить и на последний вопрос задачи о значении Поскольку лежит на третьей параболе. Значит,
Следующие упражнения на применение диаграмм Юнга.
Решая задачу М1065, мы проделали большую работу. Нельзя ли снова воспользоваться производящими функциями и извлечь из равенства какое-нибудь красивое тождество?
Заменяя произведение на по мы преобразуем левую
и мы получаем следующую формулу:
Эти две формулы получены Гауссом. Нечего и говорить, что это удивительно красивые формулы!
В заключение я хочу познакомить вас с двумя знаменитыми тождествами теории разбиений, для которых до сих пор не найдено прозрачных доказательств, хотя эта задача и по сей день остаётся в сфере интересов многих математиков.
Конечно, закономерность, утверждаемая этими тождествами, в высшей степени красива и нетривиальна, и неудивительно, что крупнейший английский математик начала XX века Г. Харди, узнавший о них из письма Рамануджана, датированного 16 января 1913 года, пришёл в восхищение. *)
При чтении этой статьи у вас, может быть, сложилось впечатление, будто теория разбиений напоминает кунсткамеру, в которую заботливо собраны различные экзотические экспонаты, никак или почти никак между собой не связанные. До недавнего времени так оно и было. Ситуация коренным образом изменилась лишь в XX века, когда английскому математику Яну Макдональду удалось найти единый подход к доказательству большого класса тождеств теории разбиений и открыть много новых, объединив их в стройную теорию (тождество ГауссаЯкоби включается в неё). **) Для тождеств РоджерсаРамануджана и многих аналогичных тождеств общего подхода не найдено, хотя в последнее время и появились алгебраические методы их доказательств. Так что, понимание истинной природы этих тождеств, вероятно, ещё впереди.
Разбиения чисел
Задача
В левом столбце таблицы выписаны все способы, которыми можно записать число 7 в виде суммы различных натуральных слагаемых («строгие разбиения»). В правом — все способы, которыми можно записать это же число в виде суммы нечётных слагаемых («нечётные разбиения»).
| Строгие разбиения | Нечётные разбиения |
| 7 = 7 | 7 = 7 |
| 7 = 6 + 1 | 7 = 5 + 1 + 1 |
| 7 = 5 + 2 | 7 = 3 + 3 + 1 |
| 7 = 4 + 3 | 7 = 3 + 1 + 1 + 1 + 1 |
| 7 = 4 + 2 + 1 | 7 = 1 + 1 + 1 + 1 + 1 + 1 + 1 |
Пусть s(n) — количество строгих разбиений числа n, а o(n) — количество нечётных разбиений. Докажите, что s(n) = o(n).
Подсказка 1
Чтобы доказать, что количества элементов в двух множествах одинаковы, бывает удобно установить между ними взаимно-однозначное соответствие.
Подсказка 2
Пусть есть какое-то разбиение на различные слагаемые. Из него можно получить разбиение на нечётные слагаемые, если каждое чётное число разбивать на две половинки до тех пор, пока не останутся только нечётные.
Пример: 20 + 6 + 3 → 10 + 10 + 3 + 3 + 3 → 5 + 5 + 5 + 5 + 3 + 3 + 3.
А как по «нечетному» разбиению получить исходное «строгое»? Вот это и есть суть задачи.
Решение
Утверждение задачи впервые было доказано Леонардом Эйлером около 1740 года с помощью производящих функций.
Леонард Эйлер (1707–1783). Портрет работы Я. Э. Хандманна, 1753 г. Изображение с сайта ru.wikipedia.org
Теорема Эйлера. Количество разбиений числа N на попарно различные слагаемые («строгие разбиения») равно количеству разбиений N на нечётные слагаемые («нечётные разбиения»).
В подсказке был указан способ, позволяющий получить из любого строгого разбиения нечётное. Для этого каждое чётное число, входящее в разбиение на различные слагаемые, нужно было разделить пополам, то есть представить в виде суммы двух равных половинок. А затем повторять этот процесс до тех пор, пока чётных чисел не останется.
Например, из разбиения
1 13 ← (1, 2 6 ) ← (1, 4 3 ) ← (1, 4, 4 2 ) ← (1, 4, 8).
Вы уже поняли закономерность? Она столь же проста, сколь и красива: каждый «показатель степени» записывается в виде суммы различных степеней двойки (то есть выписывается его двоичная запись), после чего каждой из имеющихся степеней соответствует своё слагаемое в исходном «строгом» разбиении. Это становится совсем понятным, если сообразить, что из одного чётного слагаемого в строгом разбиении могли получиться только 2, 4, 8, 16 и т. д. нечётных — то есть «вклад» каждого слагаемого в общее количество всегда является степенью двойки, а так как равных слагаемых нет, то все степени оказываются различными.
Джеймс Уитбред Ли Глейшер (1848–1928). Изображение с сайта ru.wikipedia.org
Это замечательное соответствие было придумано в конце XIX века английским математиком Джеймсом Уитбредом Ли Глейшером (увы, его научные результаты в основном касались областей математики, которые не изучаются ни в средней школе, ни даже в нематематических вузах, поэтому широкой публике он абсолютно неизвестен). Тем не менее он был удостоен двух очень значимых математических наград своего времени — медали де Моргана в 1908 году (это высшая награда Лондонского математического общества, присуждается раз в три года) и медали Сильвестра в 1913 году (высшая награда Лондонского королевского общества).
В задаче о нечетных разбиениях заслуга Глейшера в том, что он придумал не только новый подход к решению, но и дал замечательное обобщение задачи:
Теорема Глейшера. Количество разбиений целого числа N на части, не делящиеся на число d, равно количеству разбиений N на слагаемые, в которых никакая часть не повторяется d или более раз.
Послесловие
Но рассказ о соответствиях между нечётными и строгими разбиениями был бы заведомо неполон без упоминания другого замечательного соответствия между ними, придуманного Джеймсом Джозефом Сильвестром (тем самым, в честь которого названа упомянутая выше медаль).
Джеймс Джозеф Сильвестр (1814–1897). Изображение с сайта ru.wikipedia.org
Сильвестр был, по-видимому, первым математиком, который исследовал разбиения чисел на слагаемые с помощью клетчатых картинок. Впоследствии эти картинки получили название «диаграммы Юнга» или «диаграммы Феррерса» в честь двух других британских математиков, младших современников Дж. Сильвестра.
Пусть есть разбиение на нечётные слагаемые. Сильвестр предлагал нарисовать диаграмму, в которой этим слагаемым соответствуют горизонтальные ряды (строки), причем располагать эти ряды симметрично относительно центра (это можно сделать именно благодаря нечётности всех слагаемых, рис. 1). А для установления соответствия он рассматривал «крюки», которые на рисунке 1 изображены чередующимися цветными рядами. Первый крюк идет снизу по центральному ряду до верхней строки, а потом продолжается по этой строке вправо. Следующий крюк — по соседнему слева ряду снова до верхней строки, а затем по первой строке до конца влево. Потом — снова крюк справа, но уже до второй строки, и так далее. В итоге получается уже знакомое нам по соответствию Глейшера разбиение (18, 15, 13, 9, 8, 7, 4, 1). Не правда ли, красиво? К сожалению, столь же красивого обратного соответствия Сильвестр не дал. Вместо этого он просто привёл алгебраическое доказательство того, что такое соответствие является взаимно-однозначным.
К слову, Сильвестр не ограничился одним новым соответствием, а попутно в той же работе доказал и несколько других новых фактов про нечётные и строгие разбиения. В частности, он обнаружил соответствие между нечётными разбиениями, содержащими ровно k различных чисел, и разбиениями на различные числа, содержащими ровно k «цепочек» — подпоследовательностей из идущих подряд натуральных чисел. Это привело его к следующей теореме.
Теорема Сильвестра (1882). Количество разбиений числа N на нечётные части, среди которых ровно k различных чисел, равно количеству разбиений N на различные части, в которых встречаются ровно k цепочек.
Ясно, что исходный результат Эйлера получается в качестве следствия из теоремы Сильвестра — простым сложением по всем k.
Однако математика не стоит на месте, и красивое соответствие все-таки было найдено, причём совсем недавно, в самом конце ХХ века. Сделали это два корейских математика Ким Донсу и И Эчжа (в тот момент второй из них был еще студентом, а ныне он — профессор в Университете штата Пенсильвания). Я приведу картинку, взятую из их статьи A note on partitions into distinct parts and odd parts, и кратко прокомментирую ее, предоставляя возможность читателю самостоятельно додумать детали.
Нарисуем картинку разбиения на различные части, начав с самых маленьких частей, то есть с единицы: 1 + 4 + 7 + 8 + 9 + 13 + 15 + 18 (рис. 2). Если количество частей нечётно, то в качестве самой маленькой части добавим 0. Первую часть поместим в первую строку, вторую — в строку под ней, причем выровняв ее по левому краю первой строки. Третью часть поместим в третью строку, но выровняем ее со второй строкой по правому краю, и так далее, чередуя выравнивание по левому и по правому краям. Так как все части различны, то в результате все вертикальные края (и левые, и правые), кроме последнего, будут иметь высоту 2.
Кроме того, нарисуем жирную вертикальную черту — разделитель — на расстоянии от правого края, равном знакочередующейся сумме частей
Тогда все столбцы правее разделителя содержат нечётное число клеток (ведь каждая вертикаль состоит из одной нижней строки и чётного числа других строк) и могут рассматриваться как сумма нечётных слагаемых:
(эти числа подписаны в первом ряду под диаграммой, справа от разделителя). При этом все последовательные нечётные числа от 1 до 7 встречаются хотя бы один раз. Следовательно, к 1 можно прибавить число клеток в паре нижних строк слева от разделителя (то есть 14), к 3 — число клеток в паре следующих строк (10), к 5 — клетки из следующей пары (8), а к 7 — клетки последней пары строк (2). Эти слагаемые подписаны во второй строке под диаграммой. Наконец, в третьей строке выписаны суммы первой и второй строки — тоже нечётные, поскольку вся вторая строка состоит из чётных чисел. Ясно, что каждая клетка диаграммы учтена ровно один раз — клетки правее разделителя вошли в слагаемые первой строки. А клетки левее разделителя вошли в слагаемые второй строки. Тем самым мы получили соответствие между различными слагаемыми и нечётными слагаемыми, причём — то же самое соответствие, которое было предложено Сильвестром.
А как построить обратное соответствие? Метод Кима – И здесь во многом повторяет способ Сильвестра, но выглядит, пожалуй, даже естественнее.
Выпишем убывающую последовательность из чисел нечётного разбиения (a1 = 15, a2 = a3 = 13, a4 = 9, a5 = a6 = 7, a7 = a8 = a9 = 3, a10 = a11 = 1) и будем от первого члена отнимать 1, от второго — 3, от третьего — 5, и так далее до тех пор, пока разности будут положительны. То есть запишем равенства 15 = 1 + 14, 13 = 3 + 10, 13 = 5 + 8, 9 = 7 + 2. Это сразу даст нам нужное разбиение третьей строчки под диаграммой на первую и вторую. Затем все числа первой строчки перенесём в диаграмму справа от разделителя, а каждое чётное число второй строчки «уложим» в две строки слева от разделителя. В результате получим диаграмму, в которой нижняя строка будет самой длинной, а каждая следующая строка будет короче предыдущей. Суммируя клетки этой диаграммы по строкам, получим разбиение на различные слагаемые.
Результат Кима – И — даже при том, что они фактически просто переформулировали Сильвестра — использует понятие разделителя, которого не было в оригинале. А значит, тоже позволяет доказать более сильный факт. Но удивительно даже не это, а то, что этот факт был открыт на несколько лет раньше, чем появилась красивая картинка от корейцев!
Теорема о разбиениях на d нечётных частей (М. Буске-Мело, К. Эриксон, 1997). Количество разбиений числа N на попарно различные части, имеющие знакочередующуюся сумму d, равно количеству разбиений N на d нечётных частей.















