Что такое разброс в статистике
Что такое разброс в статистике
Необходимо отметить, что данная мера крайне неточна и неустойчива. Единственный необычно высокий или низкий результат может повлиять на величину размаха.
Дисперсия характеризует насколько частные значения отклоняются от средней величины в данной выборке. Чем больше дисперсия, тем больше отклонение или разброс данных. Дисперсия определяется по следующей формуле:
— выражение, означающее, что для всех значений x от первого до последнего в данной выборке вычисляется разность между частными и средними значениями, эти разности возводятся в квадрат и суммируются
Вычислим дисперсию ( для следующего ряда: 2, 4, 6, 8, 10. Прежде всего, найдем среднее (М) для данного ряда, оно равно 6.
Из каждого элемента ряда вычтем величину среднего этого ряда. Полученные величины характеризуют то, насколько каждый элемент отклоняется от средней величины в данном ряду. Экспериментальные данные этой задаче, необходимые для расчета дисперсии, представим в виде (табл. 5)
| Первичный результат | ||
| 2 | — 4 | 16 |
| 4 | — 2 | 4 |
| 6 | 0 | 0 |
| 8 | 2 | 4 |
| 10 | 4 | 16 |
| М = 6 |
Далее разности возводят в квадрат суммируются. Полученную сумму квадратов разностей делим на объем данной выборки. В нашем примере получится следующее:
Общий алгоритм вычисления дисперсии ( следующий:
Вычисляется среднее по выборке
Для каждого элемента выборки вычисляется его отклонение от среднего.
Каждый элемент множества возводят в квадрат.
Находится сумма этих квадратов.
Эта сумма делится на общее количество членов используемой выборки.
Эта закономерность известна как закон «трех сигм» и является одной из характеристик нормального распределения.
Разброс выборки, дисперсия, стандартное отклонение.



Кроме величин, характеризующих типичные значения выборки (мода, медиана, средние значения), существуют числовые характеристики выборочного ряда, позволяющие определить степень варьирования (изменения) измеряемого признака. Это разброс выборки, дисперсия и стандартное отклонение.
Разброс (размах) выборки – это разность между максимальной и минимальной величинами данного конкретного вариационного ряда:
Чем сильнее варьирует измеряемый признак, тем больше величина R, и наоборот.
Однако бывает, что у двух выборочных рядов и средние, и размах совпадают, а характер варьирования рядов различен. Данный факт подтверждается такими числовыми характеристиками как дисперсия и стандартное отклонение.
Дисперсия – среднее арифметическое квадратов отклонений значений переменной от её среднего значения.
D = 
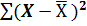
Дисперсия обозначается символами D (по генеральной совокупности) или 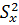
Стандартное отклонение – величина, равная квадратному корню из дисперсии: σ = 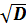
Стандартное отклонение по выборке обозначается Sx. Другое название стандартного отклонения: среднее квадратическое отклонение.
7 базовых статистических понятий, необходимых дата-сайентисту
Даже если вы хорошо программируете, но слабо ориентируетесь в статистике, вероятность выжить в Data Science очень низка.
У статистики есть несколько различных определений. Одно из самых простых и точных — это «наука о сборе и классификации цифровых данных». А если добавить к нему немного о программировании и машинном обучении, то получится неплохое описание основ Data Science.
В самом деле, в Data Science трудно найти область, где нет статистики в том или ином виде. Она нужна для:
Мы выбрали семь базовых концепций, без которых в Data Science точно не обойтись. К счастью, они не слишком сложны.
С некоторых пор утверждает, что он data scientist. В предыдущих сезонах выдавал себя за математика, звукорежиссёра, радиоведущего, переводчика, писателя. Кандидат наук, но не точных. Бесстрашно пишет о Data Science и программировании на Python.
1. Меры описательной статистики
Ключевые показатели, применяемые в описательной статистике (их ещё называют мерами или, если точнее, мерами центральной тенденции), — это:
Посмотрите это небольшое видео о среднем, медиане и моде на сайте Академии Хана — образовательного ресурса, который славится доходчивыми объяснениями. Там всё просто, на понятном русском языке.
Кроме трёх перечисленных, есть и другие статистические показатели — например, меры рассеяния. Главная из них — дисперсия, о ней ниже. Все они нужны, чтобы понять, какие перед нами данные и о чём именно они рассказывают.
2. Распределение
Внешняя форма данных, выраженная в мерах описательной статистики, даёт нам информацию об их характере. Это как в жизни: по фигуре, походке и одежде человека обычно можно догадаться о его поле, возрасте и даже профессии. В случае числовых данных мы догадываемся о распределении.
Термин пришёл из теории вероятностей, которая рассматривает любое событие в мире как имеющее ту или иную вероятность. Однородные события хоть и происходят с разной вероятностью, но подчиняются распределению, которое «раздаёт» им эти вероятности.
В Data Science распределение понимается обобщённо: это закон соответствия одной величины другой. Оно подсказывает нам, какой именно процесс может скрываться за данными, и то, насколько эти данные полны. Чуть подробнее об этом в нашей статье про математику для джунов.
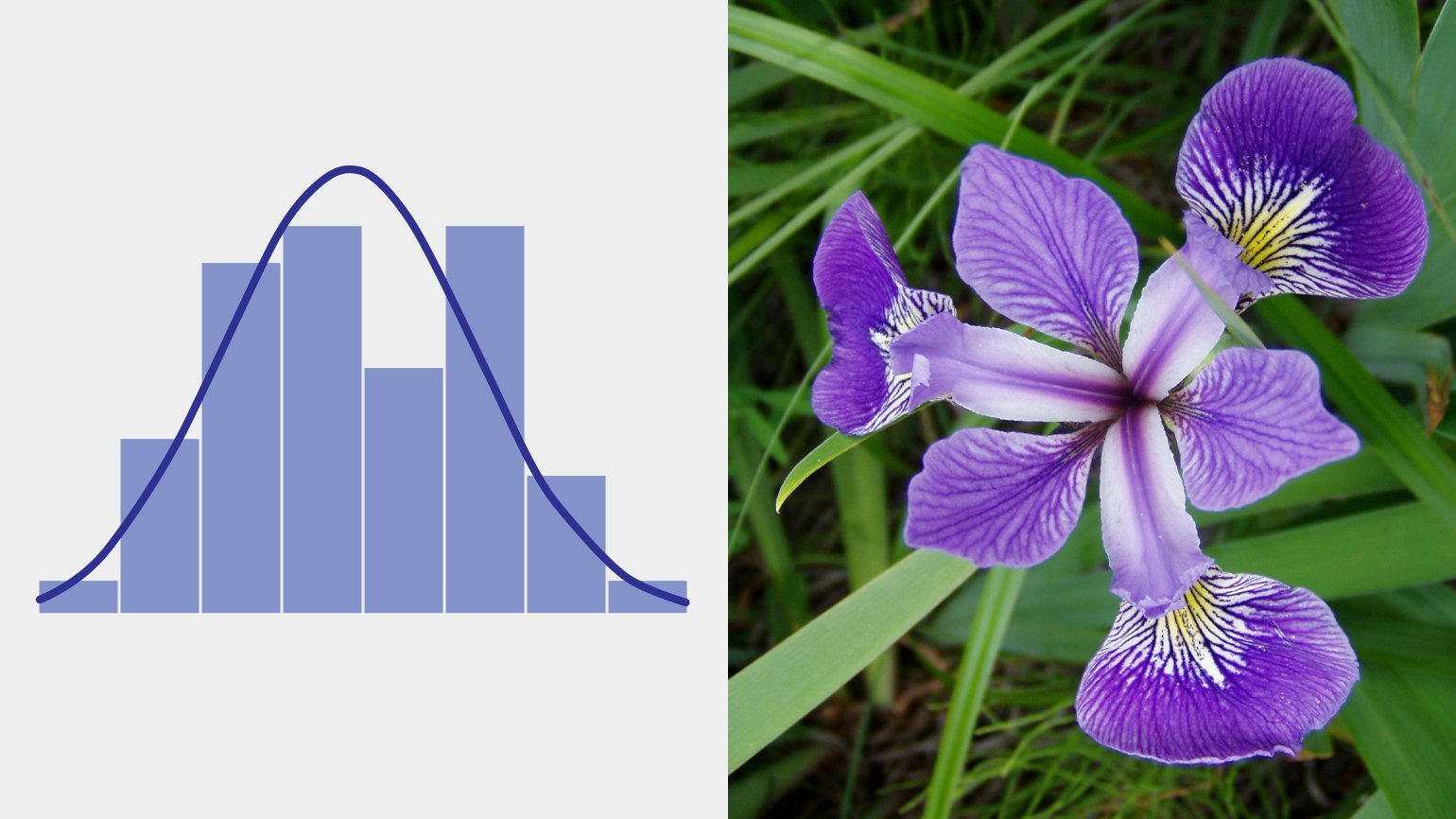
Возможно, вы уже слышали про колокол нормального распределения, или гауссиану: она описывает процессы, где результат является суммой многих случайных величин, каждая из которых слабо зависит от другой и вносит сравнительно небольшой вклад.
Величина ошибок измерения в физике, длина когтей, зубов и шерсти в биологии, объёмы речных стоков в гидрологии — все эти показатели имеют нормальное распределение. Это, пожалуй, самое распространённое в природе и не только в природе распределение, поэтому оно и названо нормальным.
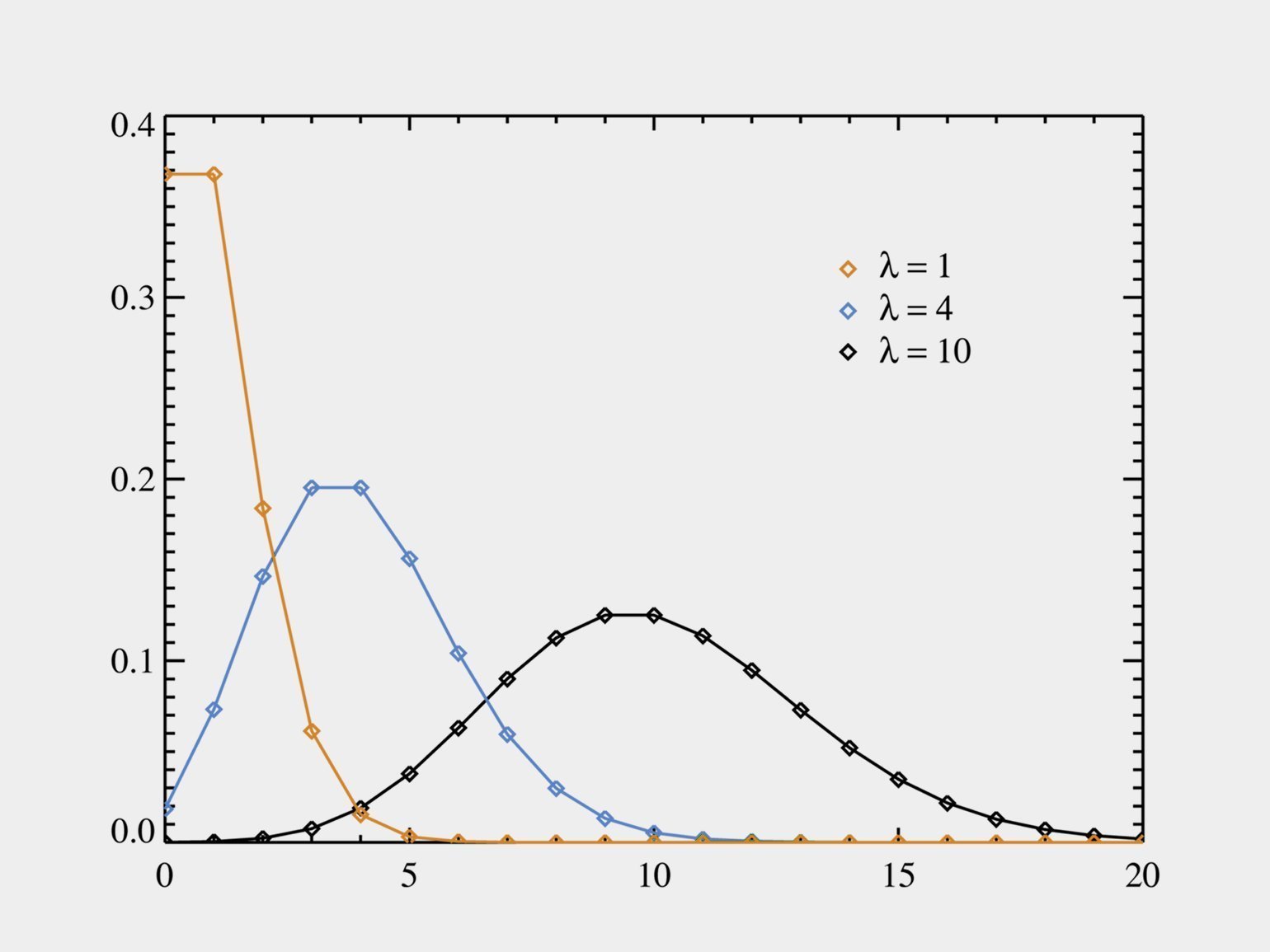
Распределение Пуассона тоже часто встречается в работе дата-сайентистов и аналитиков: это число событий за какой-то промежуток времени — при условии, что события независимы друг от друга и имеют некоторый порог интенсивности.
Это и число посетителей в торговом центре, и количество голов, забитых футбольной командой, и скорость роста колонии бактерий.
Существуют и другие распределения, в том числе довольно экзотические: Вигнера, Вейбулла, Коши. Они встречаются намного реже или преимущественно в каких-то специальных областях вроде квантовой физики. Тем не менее дата-сайентисту нужно знать графики, параметры и названия основных распределений, благо их не так много.
3. Семплирование
Предположим, вам требуется решить важную задачу: выяснить среднюю ширину морды домашних котов нашей страны. Прямой способ, то есть измерение всех домашних питомцев, невозможен по ряду объективных причин. Придётся ограничиться выборкой — взять какое-то число животных, измерить морды именно им и сделать выводы по итогам только этих исследований.
Но тут сразу же возникают вопросы:
Семплирование — это группа статистических методов и приёмов, отвечающих на эти вопросы. С помощью семплирования мы формируем нашу выборку так, чтобы она наилучшим образом отражала свойства генеральной совокупности — то есть свойства всех котов страны.
Иными словами, вы не можете измерить N первых попавшихся котов и обобщить результат для остальных. Выборка должна хорошо «сидеть» во всей популяции кошек, чтобы можно было делать обоснованные выводы. Такую выборку называют релевантной.
Кстати, статистика и котики — близнецы-братья. После выхода одноимённой книги Владимира Савельева мы говорим «статистика», а подразумеваем «котики», и наоборот. И смело рекомендуем эту книгу всем, кто дочитал до этого места.
В Data Science методы семплирования применяются при разработке, подготовке и оценке датасетов, чтобы они одновременно и были упорядоченными, и соответствовали реальности.
4. Смещение
Прочитайте нашу статью о создании простой модели машинного обучения. Она предсказывает город, в который вероятнее всего поедет турист, на основании его возраста, пола, места жительства, дохода и транспортных предпочтений. Такая рекомендательная система на минималках.
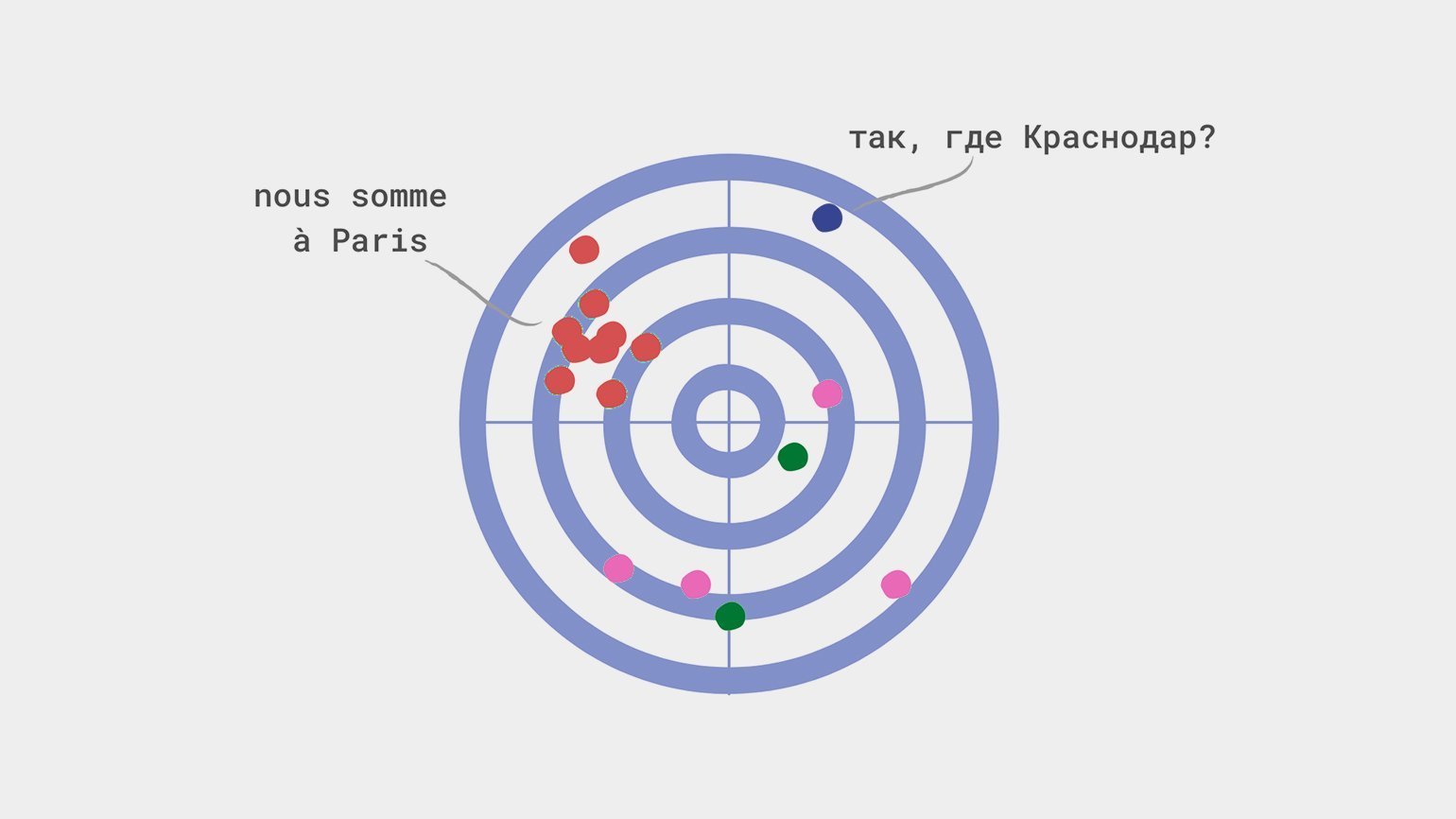
Смещение происходит, когда модель недооценивает или переоценивает какой-либо параметр. Представим, что модель из статьи выше отправляет всех краснодарцев в Париж — независимо от их дохода, предпочтений и других параметров. В этом случае мы скажем, что модель переоценивает значение параметра «Город проживания».
Чаще всего причиной смещения являются:
Когда мы неверно собираем данные, говорят о систематической ошибке отбора. Например, в прошлом веке многие считали, что во Вселенной больше голубых галактик, — впечатление возникало потому, что плёнка была более чувствительна к голубой части спектра.
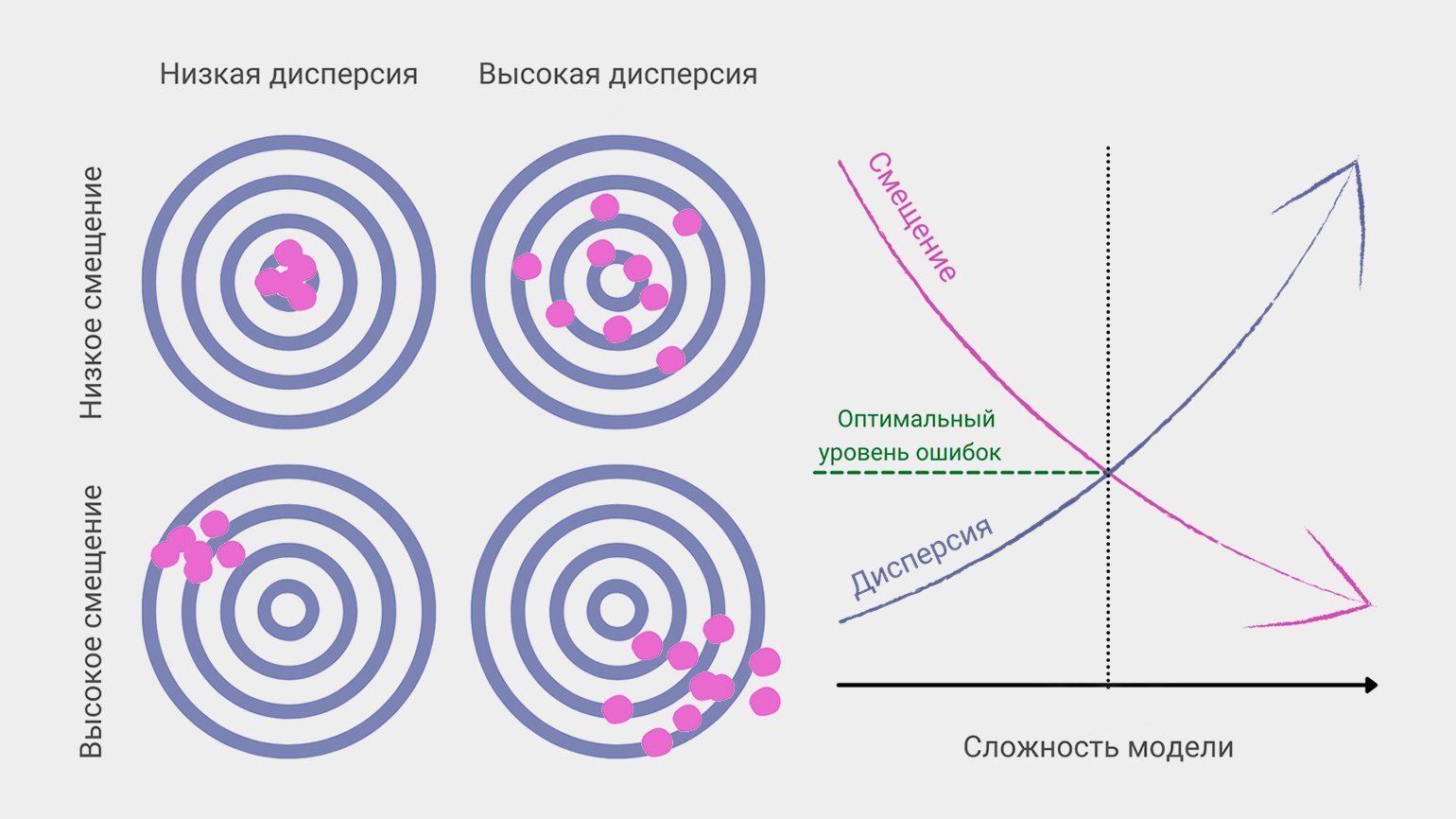
Другая ошибка — ошибка меткого стрелка — происходит, когда мы вольно или невольно отбираем в выборку только схожие между собой данные, то есть фактически рисуем мишень вокруг места, куда попадём.
Причин, вызывающих смещение, так много, что Марк Твен заметил: «Существует три вида лжи: ложь, наглая ложь и статистика». Например:
Эти и другие ошибки смещения трудно выявить статистическими методами, поэтому нужно стараться избежать их до того, как вы начнёте сбор данных.
Если пить «Боржоми» уже поздно (датасет уже сформирован), обязательно спросите себя: «Не смещены ли мои данные?» — а они наверняка смещены, «Куда и почему они смещены?» и «Можно ли с этим жить?»
5. Дисперсия
Дисперсия — это величина, показывающая, как именно и насколько сильно разбросаны значения — например, предсказания модели машинного обучения или доход за рассматриваемый период. За точку, относительно которой эти значения разбросаны, берут истинное значение, целевую переменную или математическое ожидание, которое вычисляется теоретически и заранее.
Часто в качестве матожидания выступает обычное среднее арифметическое. Например, математическое ожидание количества очков при броске игрального кубика равно среднему арифметическому очков на всех гранях:
(1 + 2 + 3 + 4 + 5 + 6) / 6 = 21/6 = 3,5
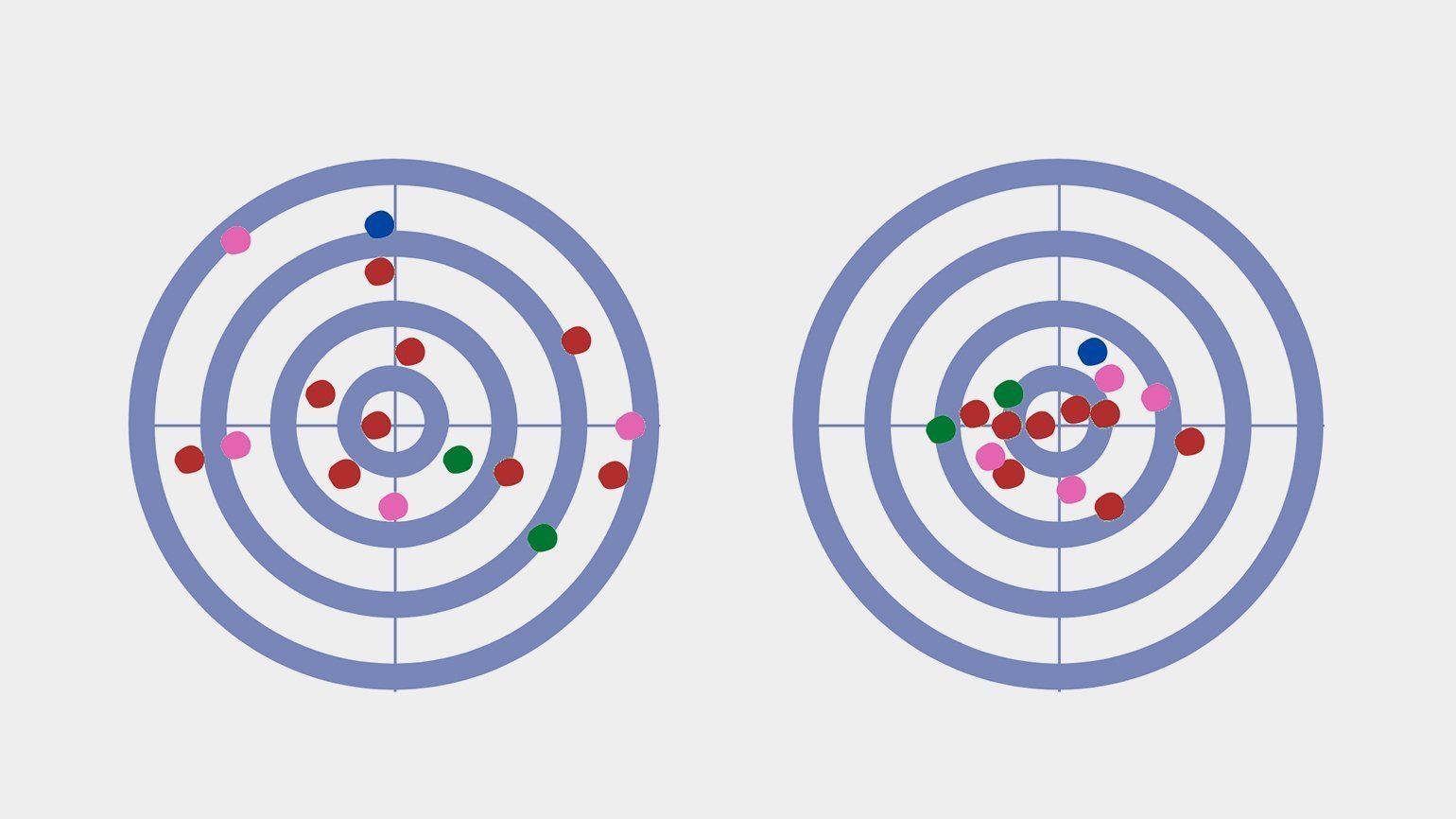
Представьте себе тир, стрелка и мишень. Снайпер стреляет в стандартный круг, где попадание в центр даёт 10 баллов, в зависимости от удаления от центра количество баллов снижается, а крайние области дают всего 1 балл. Каждый выстрел стрелка — это случайное целое значение от 1 до 10.
Изрешечённая пулями мишень — отличная иллюстрация распределения. Дисперсия здесь — величина, обратная кучности попаданий: хорошая кучность означает низкую дисперсию, и наоборот.
6. Дилемма (компромисс) смещения и дисперсии
Смещение и дисперсия вместе составляют итоговую ошибку предсказания модели машинного обучения. В идеальном мире и смещение маленькое, и дисперсия низкая. На практике это связано в дилемму: уменьшение одной из величин неизбежно приводит к росту другой.
Если не вдаваться в детали, обучение модели — это построение функции, график которой лучше всего ложится на точки из тренировочного набора данных.
Модель может нарисовать нам довольно сложную и заковыристую функцию, график, который хорошо охватывает все точки в тренировочных данных. Но если наложить этот график на новые точки (то есть дать функции новые данные), она сработает хуже — так и получается смещение.
С другой стороны, обучение на разных тренировочных наборах или даже разных датасетах с большой вероятностью даст разброс в предсказаниях, то есть высокую дисперсию.
Более сложные модели дают низкое смещение, но чувствительны к шуму и колебаниям в новых данных, поэтому их предсказания разбросаны. Если при обучении наш снайпер будет учитывать незначимые факторы (вроде цвета мишени или направления магнитного поля Земли), то в другом тире, с другой винтовкой или в другую погоду точность его стрельбы упадёт.
Простые модели, напротив, упускают важные параметры и «бьют кучно, но мимо». Как другой снайпер, не приученный обращать внимание на ветер и расстояние до мишени.
В процессе настройки модели машинного обучения дата-сайентист всегда ищет компромисс между смещением и дисперсией, чтобы уменьшить общую ошибку предсказания.
Кстати, эта дилемма встречается не только в статистике и машинном обучении, но и в обучении людей. В исследовании 2009 года утверждается, что люди используют эвристику «высокое смещение + низкая дисперсия»: мы заблуждаемся, зато очень уверенно.
Учтите это, если захотите сделать свой ИИ более похожим на человека.
7. Корреляция
Когда изменения одной величины сопутствуют изменениям другой, говорят о корреляции. Главное, что необходимо о ней знать: корреляция не означает причинно-следственную связь.
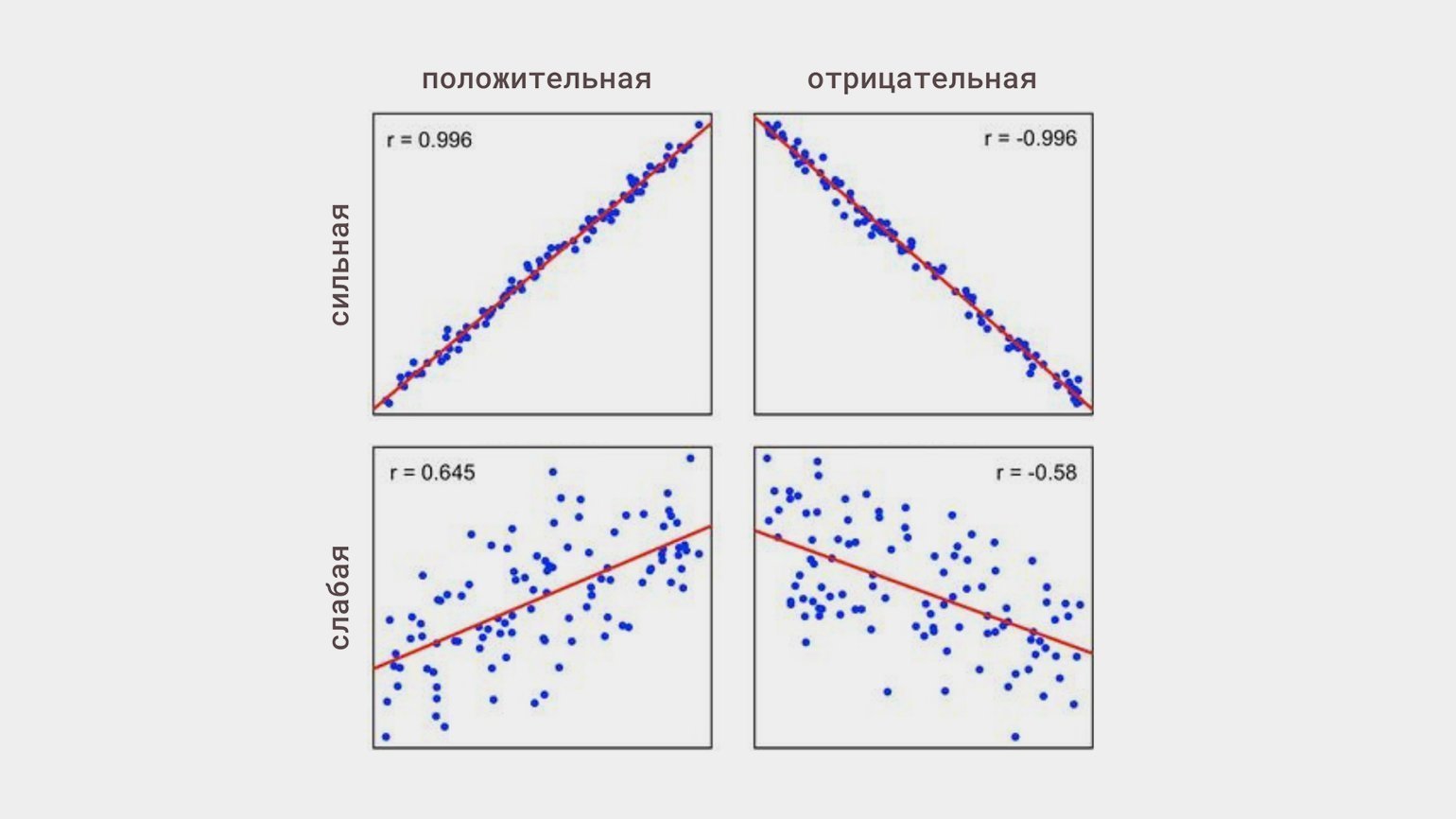
Линейная корреляция — это когда изменения одной величины пропорциональны изменениям другой. Она может быть:
Статистическую связь между переменными исследуют с помощью корреляционного анализа. Его основная задача — оценить тесноту связи (это термин) между переменными, чтобы понять, какие переменные учитывать в модели, а какие нет.
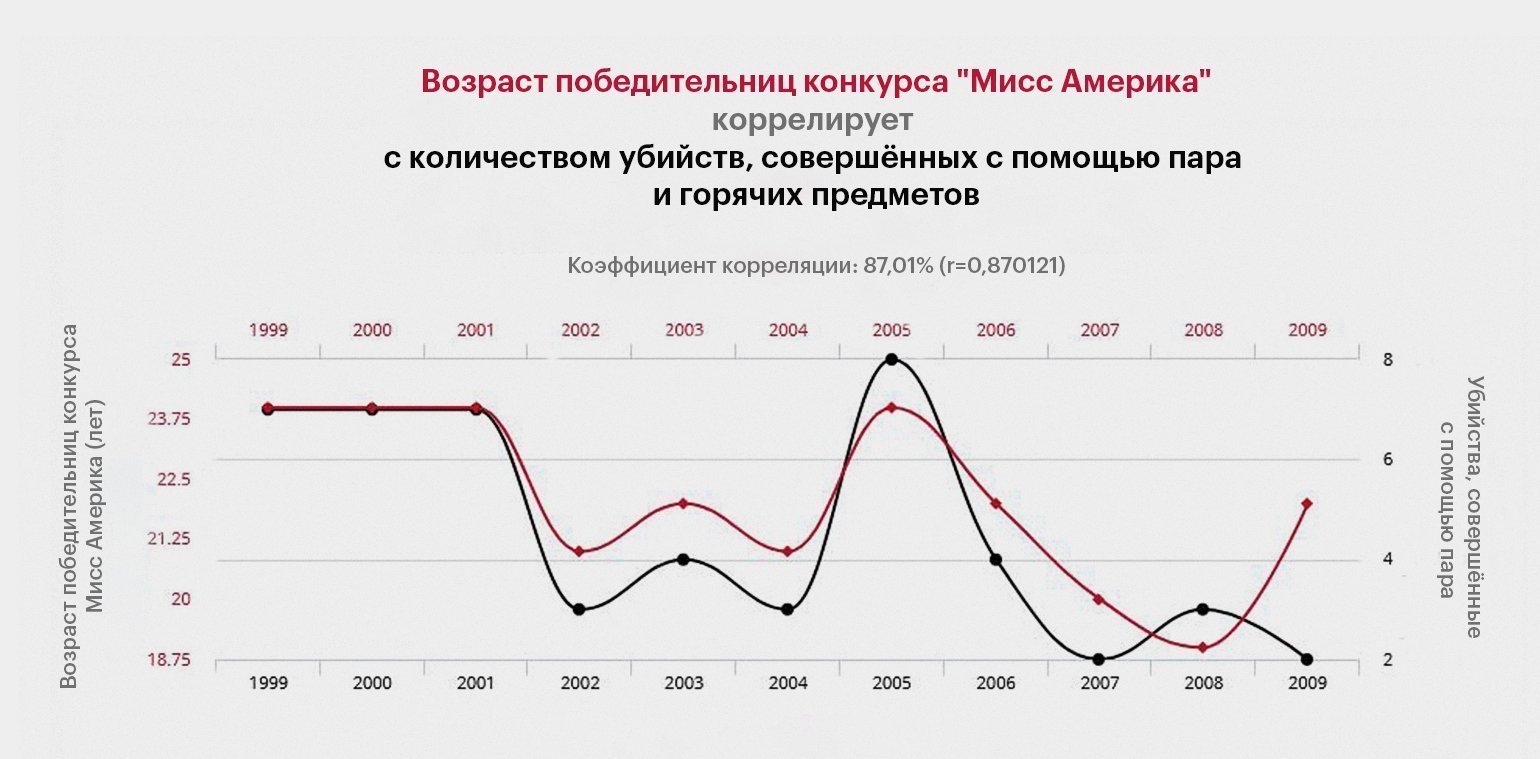
И ещё раз, потому что действительно важно: корреляция ни в коем случае не означает причинно-следственную связь. Если два показателя скоррелированы, то далеко не факт, что они хоть как-то связаны.
Кстати, проект Spurious Correlations («Ложные корреляции») публикует графики корреляций между совершенно неожиданными статистическими показателями — например, количеством людей, утонувших в домашних бассейнах, и числом фильмов с участием Николаса Кейджа.
Имеет смысл время от времени заходить по этой ссылке с целью профилактики СПГС — синдрома поиска глубинной связи.
Заключение
Data Science — не просто комбинирование модных моделей в Jupyter-ноутбуке. Профессионалы в этой области глубоко понимают природу данных и то, как они могут помочь в принятии конкретных бизнес-решений.
Всё это изучалось в статистике задолго до того, как первый дата-сайентист набрал свой первый import pandas as pd. Статистика — фундамент всей современной науки о данных, включая машинное обучение, глубокие нейросети и даже искусственный интеллект.
В нашем курсе «Профессия Data Scientist» статистике уделено самое пристальное внимание. Вы не ударите в грязь лицом ни на тусовке статистиков, ни на настоящем DS-собеседовании. Приходите!
Polina Vari для Skillbox
Для отличия статистического термина от терминов из других отраслей (музыки, биологии) часто пишут этот термин через «е», а не через «э».
Описательная статистика (англ. descriptive statistics) занимается обработкой опытных данных, их систематизацией, наглядным представлением в форме графиков и таблиц, а также их количественным описанием посредством основных статистических показателей.
Тренировочный набор, или обучающая выборка (англ. train set, training sample), — часть данных из датасета, по которой производится настройка или оптимизация модели машинного обучения.
Рекомендательные системы — программы, которые пытаются предсказать, какие объекты (фильмы, музыка, книги, новости, веб-сайты и др.) будут интересны пользователю.
Разницу между наблюдаемым значением и значением, предсказанным моделью.
Вариация, размах, межквартильный размах, среднее линейное отклонение
В этой статье мы приступим к изучению показателей вариации: размах вариации, межквартильный размах, среднее линейное отклонение.
В математической статистике вариация занимает одно из центральных мест. Что же такое вариация? Это изменчивость. Вариация показателя – изменчивость показателя.
Показатели вариации дают очень важную характеристику процессам и явлениям. Они отражают устойчивость процессов и однородность явлений. Чем меньше показатель вариации, тем более процесс устойчивый, а значит, и более предсказуемый.
Показатели вариации отражают не отдельно взятые значения, а дают характеристику некоторому явлению или процессу в целом. Имея в наличии показатели среднего значения и вариации, можно получить первичное представление о характере данных. Средняя – это обобщающий уровень, а вариация характеризует, насколько среднее значение (или другой показатель) хорошо обобщает значения некоторой совокупности данных. Если показатель вариации незначительный, то значения совокупности находятся близко к среднему, следовательно, среднее значение хорошо обобщает совокупность. Если вариация большая, то среднее значение плохо обобщает данные (значения разбросаны далеко друг от друга), и получается «средняя температура по больнице».
Размах вариации
Размах вариации – разница между максимальным и минимальным значением:
Ниже приведена графическая интерпретация размаха вариации.
Видно максимальное и минимальное значение, а также расстояние между ними, которое и соответствует размаху вариации.
С одной стороны, показатель размаха может быть вполне информативным и полезным. К примеру, максимальная и минимальная стоимость квартиры в городе N, максимальная и минимальная зарплата по профессии в регионе и проч. С другой стороны, размах может быть очень широким и не иметь практического смысла, т.к. зависит лишь от двух наблюдений. Таким образом, размах вариации очень неустойчивая величина.
Межквартильный размах
В статистике для анализа выборки часто прибегают к другому показателю вариации – межквартильному размаху. Квартиль – это то значение, которые делит ранжированные (отсортированные) данные на части, кратные одной четверти, или 25%. Так, 1-й квартиль – это значение, ниже которого находится 25% совокупности. 2-й квартиль делит совокупность данных пополам (то бишь медиана), ну и 3-й квартиль отделяет 25% наибольших значений. Так вот межквартильный размах – это разница между 3-м и 1-м квартилями. У данного показателя есть одно неоспоримое преимущество: он является робастным, т.е. не зависит от аномальных отклонений.
Наглядное отображение размаха вариации и межкварительного расстояния производят с помощью диаграммы «ящик с усами».
Среднее линейное отклонение
Есть показатели вариации, которые учитывают сразу все значения, а не только отдельные наблюдения (типа максимума или минимума). Одним из таких является среднее линейное отклонение. Этот показатель характеризует меру разброса значений вокруг их среднего. В чем суть? Для того, чтобы показать меру разброса данных, нужно вначале определиться, относительно чего этот самый разброс будет считаться. Обычно это среднее арифметическое. Далее нужно посчитать, насколько каждое значение отклоняется от средней. Нас интересует среднее из таких отклонений. Однако напрямую складывать положительные и отрицательные отклонения нельзя, т.к. они взаимоуничтожатся и их сумма будет равна нулю. Поэтому все отклонения берутся по модулю. Средне линейное отклонение рассчитывается по формуле:
a – среднее линейное отклонение,
X – анализируемый показатель,
X̅ – среднее значение показателя,
n – количество значений в анализируемой совокупности данных.
Рассчитанное по этой формуле значение показывает среднее абсолютное отклонение от средней арифметической. Наглядная картинка в помощь.
Отклонения каждого наблюдения от среднего указаны маленькими стрелочками. Именно они берутся по модулю и суммируются. Потом все делится на количество значений.
Для полноты картины нужно привести еще и пример. Допустим, имеется фирма по производству черенков для лопат. Каждый черенок должен быть 1,5 метра длиной, но, что еще важней, все должны быть одинаковыми или, по крайней мере, плюс-минус 5 см. Однако нерадивые работники то 1,2 м отпилят, то 1,8 м. Дачники недовольны. Решил директор провести статистический анализ длины черенков. Отобрал 10 штук и замерил их длину, нашел среднюю и рассчитал среднее линейное отклонение. Средняя получилась как раз, что надо – 1,5 м. А вот среднее линейное отклонение вышло 0,16 м. Вот и получается, что каждый черенок длиннее или короче, чем нужно, в среднем на 16 см. Есть, о чем поговорить с работниками.
На этом сегодняшнюю заметку закончим. В следующей статье будут рассмотрены такие показатели вариации, как дисперсия, среднеквадратичное отклонение и коэффициент вариации.