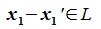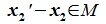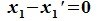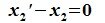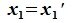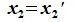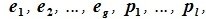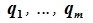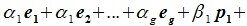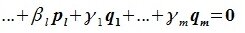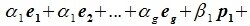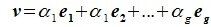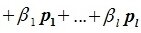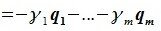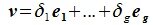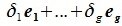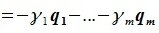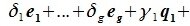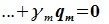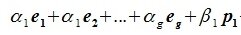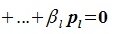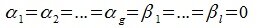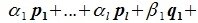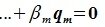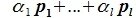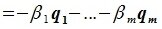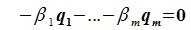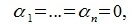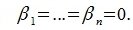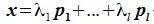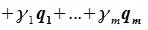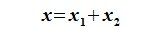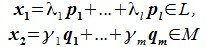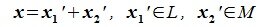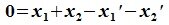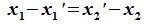Что такое размерность векторного пространства

Тема 2. Лекция 6. Векторное пространство

Лекция 6. Векторное пространство.

1. Векторное линейное пространство.

2. Базис и размерность пространства.

3. Ориентация пространства.

4. Разложение вектора по базису.

5. Координаты вектора.

1. Векторное линейное пространство.

Для этого частного случая можно дать следующее определение век-торного пространства.

Более важным как в теоретическом, так и в прикладном отношении яв-ляется общее (абстрактное) понятие векторного пространства.

1) сложение коммутативно, т. е. ;

2) сложение ассоциативно, т. е. ;

3) существует такой элемент (нулевой вектор), что для любого ;

5) для любых векторов и и любого чис-ла λ имеет место равенство ;

6) для любых векторов и любых чисел λ и µ справедливо равенство ;

7) для любого и любых чисел λ и µ справедли-во ;

8) для любого .

Из аксиом, определяющих векторное пространство, вытекают прос-тейшие следствия :

1. В векторном пространстве существует только один нуль – элемент – нулевой вектор.

2. В векторном пространстве каждый вектор имеет единственный проти-воположный вектор.

3. Для каждого элемента выполняется равенство .

4. Для любого действительного числа λ и нулевого вектора выпол-няется равенство .

5. Из равенства следует одно из двух равенств:

6. Вектор является противоположным для любого вектора .

Существование противоположного вектора определяет возможность вве-дения для вектора рассматриваемого пространства операцию вычитания как операцию, обратную операции сложения.

Разностью векторов называется вектор , удовлетворяющий равенству .

Разность векторов обозначается так : .

Итак, действительно, и множество всех геометрических векторов являет-ся линейным (векторным) пространством, так как для элементов этого мно-жества определены действия сложения и умножения на число, удовлетворя-ющие сформулированным аксиомам.

2. Базис и размерность пространства.

Существенными понятиями векторного пространства являются понятия базиса и размерность.

Базисом множества векторов, расположенных на произвольной прямой, можно считать один коллинеарный этой прямой вектор .

Базисом на плоскости назовем два неколлинеарных вектора на этой пло-скости, взятые в определенном порядке .

Базисом в обычном пространстве – три некомпланарных вектора, взя-тые в определенном порядке .

Наибольшее число линейно независимых векторов пространства называ-ется размерностью этого пространства, т. е. размерность пространства сов-падает с числом базисных векторов этого пространства.

Итак, в соответствии с данными определениями :

1. Одномерным пространством V1 является прямая линия, а базис состо-ит из одного коллинеарного вектора .

2. Двумерным пространством V2 является плоскость, базис этого прост-ранства состоит из двух неколлинеарных векторов .

Отсюда мы видим, что число базисных векторов на прямой, на плос-кости, в реальном пространстве совпадает с тем, что в геометрии принято на-зывать числом измерений (размерностью) прямой, плоскости, пространства. Поэтому естественно ввести более общее определение.

Замечание 1. В каждом пространстве можно указать сколько угодно базисов, но при этом все базисы данного пространства состоят из одного и того же числа векторов.

Замечание 2. В n – мерном векторном пространстве базисом назы-вают любую упорядоченную совокупность n линейно независимых векторов.

3. Ориентация пространства.

Пусть базисные векторы в пространстве V3 имеют общее начало и упорядочены, т. е. указано какой вектор считается первым, какой – вторым и какой – третьим. Например, в базисе век-торы упорядочены согласно индек-сации.

Можно показать, что множество всех базисов пространства распадается на два класса, т. е. на два непересекающихся подмножества.

а) все базисы, принадлежащие одному подмножеству (классу), имеют одинаковую ориентацию (одноименные базисы) ;

Рис. 1.8. Правый базис (а) и левый базис (б)

Обычно положительным базисом объявляется правый базис пространства

Правый (левый) базис пространства может быть определен и с помощью правила «правого» («левого») винта или буравчика.

По аналогии с этим вводится понятие правой и левой тройки некомпла-нарных векторов , которые должны быть упорядочены (рис.1.8).

Таким образом, в общем случае две упорядоченные тройки некомпла-нарных векторов имеют одинаковую ориентацию (одноименны) в пространстве V3 если они обе правые или обе левые, и – противоположную ориентацию (разноименны), если одна из них правая, а другая левая.

Аналогично поступают и в случае пространства V2 (плоскости).

4. Разложение вектора по базису.

Пусть — линейно независимые векторы (базис) пространства R3 а — произвольный вектор этого пространства.

Теорема. Любой вектор пространства R3 однозначно представим в виде линейной комбинации трех линейно независимых век-торов этого пространства, т. е.

(3)

Представление произвольного вектора в виде линейной комбинации ба-зисных векторов называется разложением этого вектора по базису.

Например, выражение означает, что вектор разложен по базису .

5. Координаты вектора.

5.1. Понятие о координатах вектора.

Определение. Если — базис и вектор , то числа называются координатами вектора в данном базисе.

Обозначение : или, в конкретном случае .

Вполне очевидно, что если в пространстве R выбрать другой базис, то тот же вектор будет иметь другие координаты.

5.2. Условие коллинеарности двух векторов.

Пусть векторы и разложены по базису :

Известно, что два вектора коллинеарны тогда и только тогда, когда они линейно зависимы, т. е. , где хотя бы одно из чисел λ1 или λ2 отличны от нуля.

Для определенности положим . Тогда

Откуда соотношение между координатами векторов (на основе аксиомы 5)

(7) Следовательно, необходимым и достаточным условием коллинеарности двух векторов является пропорциональность их соответствующих координат в данном базисе.

1. Векторное пространство характеризуется размерностью, базисом и ориентацией.

2. Каждый вектор пространства R n разлагается по его базису единствен-

ственным способом, коэффициенты при базисных векторах в этом разложе-нии называются координатами вектора.

Источник

Векторное пространство: база и размерность, аксиомы, свойства

Содержание:

А векторное пространство непустое множествоV=<или, v, ш, ……>, элементами которого являются векторы. С ними проводят некоторые важные операции, среди которых выделяются следующие:

— Сумма между двумя векторами u + v какие результаты z, который принадлежит множеству V.

— Умножение действительного числа α на вектор v: α v что дает другой вектор Y который принадлежит V.

Аксиомы и свойства

Чтобы векторное пространство было задано, должны быть выполнены следующие восемь аксиом:

1-переключаемый: или +v = v +или

2-транзитивность: (или + v) + ш = или + ( v + ш)

3-Существование нулевого вектора 0 такой, что 0 + v = v

5-Дистрибутивность произведения по векторной сумме: α ( или + v ) = αили +αv

6-Дистрибутивность произведения относительно скалярной суммы: (α + β)v = αv +βv

7-ассоциативность скалярного произведения: α (β v) = (α β)v

8-число 1 является нейтральным элементом, поскольку: 1v = v

Примеры векторных пространств

Пример 1

Сумму двух векторов на плоскости можно определить как операцию геометрического переноса второго вектора после первого. Результатом суммы является ориентированный сегмент, который начинается от начала первого и достигает вершины второго.

На рисунке видно, что сумма в R² коммутативна.

Мы также определяем произведение числа α и вектора. Если число положительное, направление исходного вектора сохраняется, а размер в α раз больше исходного вектора. Если число отрицательное, направление противоположное, и размер результирующего вектора является абсолютным значением числа.

Вектор напротив любого вектора v это –v =(-1) v.

Все сказанное проиллюстрировано на рисунке 2.

Пример 2

Задавать п всех многочленов степени меньше или равной двум, включая нулевую степень, образуют набор, который удовлетворяет всем аксиомам векторного пространства.

Пусть многочлен P (x) = a x² + b x + c и Q (x) = d x² + e x + f

Определяется сумма двух многочленов: P (x) + Q (x) = (a + d) x² + (b + e) ​​x + (c + f)

Сумма многочленов, принадлежащих множеству п он коммутативен и транзитивен.

Нулевой многочлен, принадлежащий множеству п тот, у которого все коэффициенты равны нулю:

Сумма скаляра α по многочлену определяется как: α P (x) = α ∙ a x² + α ∙ b x + α ∙ c

Из всего вышесказанного следует, что множество п всех многочленов степени меньше или равной двум, это векторное пространство.

Пример 3

Задавать M всех матриц из m строк x n столбцов, элементы которых являются действительными числами, образуют вещественное векторное пространство относительно операций сложения матриц и произведения числа на матрицу.

Пример 4

Множество F непрерывных функций действительной переменной образуют векторное пространство, поскольку можно определить сумму двух функций, умножение скаляра на функцию, нулевую функцию и симметричную функцию. Они также выполняют аксиомы, характеризующие векторное пространство.

База и размерность векторного пространства

Основание

Базис векторного пространства определяется как набор линейно независимых векторов, так что любой вектор этого векторного пространства может быть сгенерирован из их линейной комбинации.

Линейное объединение двух или более векторов состоит из умножения векторов на некоторый скаляр и последующего векторного сложения.

Например, в векторном пространстве векторов в трех измерениях, образованном R³, используется канонический базис, определяемый единичными векторами (с величиной 1). я, j, k.

куда я = ( 1, 0, 0 ); j = ( 0, 1, 0 ); k = (0, 0, 1). Это декартовы или канонические векторы.

Любой вектор V принадлежащий R³, записывается как V = а я + b j + c k, который представляет собой линейную комбинацию базовых векторов я, j, k. Скаляры или числа a, b, c известны как декартовы компоненты V.

Также сказано, что базовые векторы векторного пространства образуют генераторную установку векторного пространства.

Размер

Основания векторного пространства не уникальны, но все основания одного векторного пространства имеют одинаковую размерность.

Векторное подпространство

Примером векторного подпространства являются векторы, принадлежащие плоскости XY. Это подпространство является подмножеством векторного пространства размерности больше, чем набор векторов, принадлежащих трехмерному пространству XYZ.

Другой пример векторного подпространства S1 векторного пространства S, образованного всеми матрицами 2 × 2 с действительными элементами, определяется ниже:

С другой стороны, S2, определенный ниже, хотя и является подмножеством S, не образует векторное подпространство:

Решенные упражнения

-Упражнение 1

Пусть векторы равны V1=(1, 1, 0); V2= (0, 2, 1) и V3= (0, 0, 3) в R³.

а) Покажите, что они линейно независимы.

б) Покажите, что они образуют базис в R³, поскольку любую тройку (x, y, z) можно записать как линейную комбинацию V1, V2, V3.

в) Найдите компоненты тройки V= (-3,5,4) у основания V1, V2, V3.

Решение

Критерий демонстрации линейной независимости состоит в установлении следующей системы уравнений относительно α, β и γ

α (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3) = (0, 0, 0)

Чтобы получить значения α, β и γ, мы предлагаем следующую систему уравнений:

Ответ на

Сделан вывод, что это набор линейно независимых векторов в R³.

Ответ б

Теперь давайте запишем тройку (x, y, z) как линейную комбинацию V1, V2, V3.

(x, y, z) = α V1 + β V2 + γ V3 = α (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3)

α ∙ 1 + β ∙ 0 + γ ∙ 0 = x

α ∙ 1 + β ∙ 2 + γ ∙ 0 = y

α ∙ 0 + β ∙ 1 + γ ∙ 3 = z

Первый указывает α = x, второй β = (y-x) / 2 и третий γ = (z- y / 2 + x / 2) / 3. Таким образом, мы нашли образующие α, β и γ любой тройки R³

Ответ c

Перейдем к поиску составляющих тройного V= (-3,5,4) у основания V1, V2, V3.

Подставляем соответствующие значения в выражения для генераторов, найденные выше.

Мы делаем вывод, что V1, V2, V3 образуют базис в векторном пространстве R³ размерности 3.

-Упражнение 2.

Решение

P (t) = x P1 (t) + y P2 (t) + z P3 (t)

где числа x, y, z подлежат определению.

Умножая и группируя члены с одинаковой степенью по t, получаем:

Это приводит нас к следующей системе уравнений:

Решениями этой системы уравнений являются:

-Упражнение 3.

Решение

Мы линейно объединяем три вектора v1, v2, v3 и мы требуем, чтобы комбинация добавляла нулевой элемент R⁴

к v1 + b v2 + c v3 = 0

Это приводит нас к следующей системе уравнений:

Если мы подставим этот результат в первое уравнение, мы придем к выводу, что b = 0.

Наконец, a = b = c = 0, так что можно сделать вывод, что векторы v1, v2 и v3 линейно независимы.

Источник

Подпространство линейного пространства

Определение и размерность подпространства

Определение 6.1. Подпространством L n-мерного пространства R называется множество векторов, образующих линейное пространство по отношению к действиям, которые определены в R.

Другими словами, L называется подпространством пространства R, если из x, y∈L следует, что x+y∈L и если x∈L, то λ x∈L, где λ— любое вещественное число.

Простейшим примером подпространства является нулевое подпространство, т.е. подмножество пространства R, состоящее из единственного нулевого элемента. Подпространством может служить и все пространство R. Эти подпространства называются тривиальными или несобственными.

Подпространство n-мерного пространства конечномерно и его размерность не превосходит n: dim L≤ dim R.

Сумма и пересечение подпространств

Cуммой L+M называется множество векторов x+y, где x∈L и y∈M. Очевидно, что любая линейная комбинация векторов из L+M принадлежит L+M, следовательно L+M является подпространством пространства R (может совпадать с пространством R).

Пересечением L∩M подпространств L и M называется множество векторов, принадлежащих одновременно подпространствам L и M (может состоять только из нулевого вектора).

Теорема 6.1. Сумма размерностей произвольных подпространств L и M конечномерного линейного пространства R равна размерности суммы этих подпространств и размерности пересечения этих подпространств:

dim L+dim M=dim(L+M)+dim(L∩M).

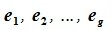
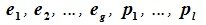
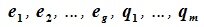
Доказательство. Обозначим F=L+M и G=L∩M. Пусть G g-мерное подпространство. Выберем в нем базис . Так как G⊂L и G⊂M, следовательно базис G можно дополнить до базиса L и до базиса M. Пусть базис подпространства L и пусть базис подпространства M. Покажем, что векторы

составляют базис F=L+M. Для того, чтобы векторы (6.1) составляли базис пространства F они должны быть линейно независимы и любой вектор пространства F можно представить линейной комбинацией векторов (6.1).

Докажем линейную независимость векторов (6.1). Пусть нулевой вектор пространства F представляется линейной комбинацией векторов (6.1) с некоторыми коэффициентами:

Левая часть (6.3) является вектором подпространства L, а правая часть является вектором подпространства M. Следовательно вектор

принадлежит подпространству G=L∩M. С другой стороны вектор v можно представить линейной комбинацией базисных векторов подпространства G:

Из уравнений (6.4) и (6.5) имеем:

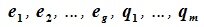
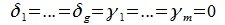
Но векторы являются базисом подпространства M, следовательно они линейно независимы и . Тогда (6.2) примет вид:

В силу линейной независимости базиса подпространства L имеем:

Так как все коэффициенты в уравнении (6.2) оказались нулевыми, то векторы

Изучая базисы подпространств L и M и базис подпространства F=L+M (6.10), имеем: dim L=g+l, dim M=g+m, dim (L+M)=g+l+m. Следовательно:

dim L+dim M−dim(L∩M)=dim(L+M). ■

Прямая сумма подпространств

Определение 6.2. Пространство F представляет собой прямую сумму подпространств L и M, если каждый вектор x пространства F может быть единственным способом представлен в виде суммы x=y+z, где y∈ L и z∈M.

Прямая сумма обозначается L⊕M. Говорят, что если F=L⊕M, то F разлагается в прямую сумму своих подпространств L и M.

Теорема 6.2. Для того, чтобы n-мерное пространство R представляло собой прямую сумму подпространств L и M, достаточно, чтобы пересечение L и M содержало только нулевой элемент и чтобы размерность R была равна сумме размерностей подпространств L и M.

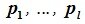
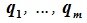
Доказательство. Выберем некоторый базис в подпространстве L и некоторый базис в подпространстве M. Докажем, что

является базисом пространства R. По условию теоремы размерность пространства R n равна сумме подпространств L и M (n=l+m). Достаточно доказать линейную независимость элементов (6.11). Пусть нулевой вектор пространства R представляется линейной комбинацией векторов (6.11) с некоторыми коэффициентами:

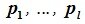
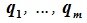
Но векторы и являются базисами подпространств L и M соответственно. Следовательно они линейно независимы. Тогда

Установили, что (6.12) справедливо лишь при условии (6.15), а это доказывает линейную независимость векторов (6.11). Следовательно они образуют базис в R.

Пусть x∈R. Разложим его по базису (6.11):

Из (6.17) и (6.18) следует, что любой вектор из R можно представить суммой векторов x₁∈L и x₂∈M. Остается доказать что это представление является единственным. Пусть кроме представления (6.17) есть и следующее представление:

Вычитая (6.19) из (6.17), получим

Так как , и L∩M= 0, то и . Следовательно и . ■

Источник