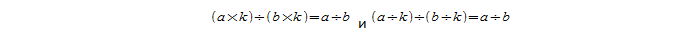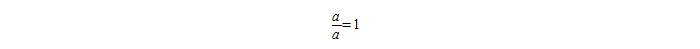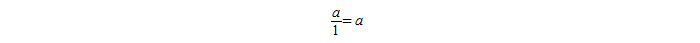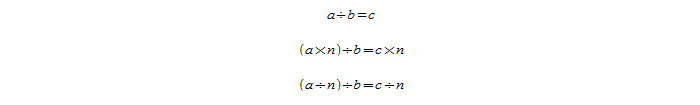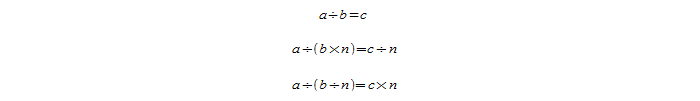Что такое разность частного чисел
Математика – царица наук. Она хоть и сложна, и многие боятся некоторых запутанных формул и вычислений, но все они состоят из простых арифметических действий сложения, вычитания, умножения и деления.
Производные операции от этих действий называются суммой, разностью, произведением и частным. Что такое частное в математике и каковы его главные свойства – будет подробно рассказано далее.
Основное свойство частного
Деление – это арифметическая операция, обратная умножению. С ее помощью можно просто узнать, сколько в первом числе содержится значений второго.
По аналогии с умножением, которое способно заменить собой многократное сложение, дробление способно заменить многократное вычитание.
Например, необходимо разделить 10 на 2. Это означает, что требуется узнать, сколько раз число 2 содержится в 10. Делая это вычитанием можно получить следующее:
10 — 2 — 2 — 2 — 2 — 2 = 0.
Проводя постепенное вычитание до нуля, можно определить, что двойка содержится в десятке ровно 5 раз и не образует остаток. Сделать это можно было однократно поделив два значения:
Частное чисел – это итог процесса деления одного значения на второе. Пример:
Одно из важнейших правил деления частного, называемое основным свойством частного, заключается в том, что если делимое и делитель умножить или разделить на одно и то же число, то итог этой операции и, соответственно частное, не изменится:
При делении числа самого на себя результатом всегда будет единица, то есть справедливо равенство:
Справедливо и другое правило: если разделить определенную величину на единицу, то итогом процесса будет сама эта величина, то есть делимое:
Увеличение или уменьшение делимого
Некоторые другие соотношения вытекают из этих. Например, если увеличить или уменьшить делимое в n раз, то в результате частное также повысится или понизится в n раз соответственно.
Изложенное правило имеет такой вид:
12 ⁄ 2 = 6 и пусть n = 3.
Проведём увеличение и уменьшение делимого:
То есть, в три раза увеличив делимое, можно в три раза увеличить частное. Аналогично выполняется и уменьшение.
Увеличение или уменьшение делителя
Следующее правило звучит так: если увеличить или уменьшить делитель в n раз, то результат деления понизится или повысится в n-нное количество раз:
Для примера требуется взять частное двух значений 54 и 6:
a / b = c и пусть n = 3.
Проведём увеличение и уменьшение делителя:
Увеличив делитель в 3 раза, во столько же раз уменьшили частное. Уменьшив делитель в три раза, делитель, напротив, увеличился в три раза.
Проверить эти «законы» можно в любом онлайн калькуляторе или вручную в уме или на бумаге.
Данные правила являются фундаментальными и составляют базу арифметики, с которой начинается математика и остальные области знаний.
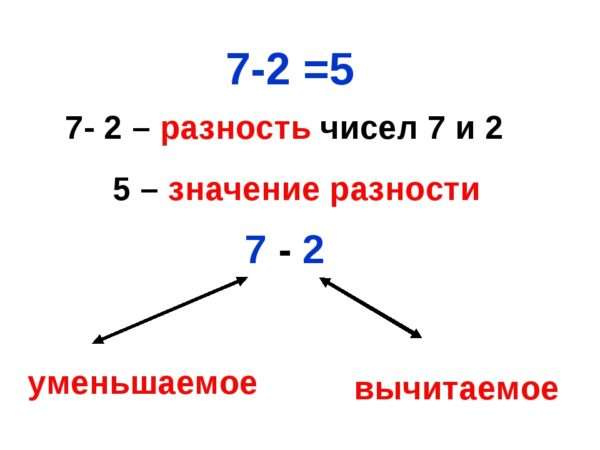
Что такое вычитаемое уменьшаемое и разность: правило
Существуют четыре основных арифметических действия: сложение, вычитание, умножение и деление. Они – основа математики, с их помощью производятся все остальные, более сложные вычисления. Сложение и вычитание – простейшие из них и взаимно противоположны. Но с терминами, используемыми при сложении, мы чаще сталкиваемся в жизни.
Говорим о «сложении усилий» при старании совместно получить нужный результат, о «слагаемых достигнутого успеха» и т.п. Названия же, связанные с вычитанием, остаются в пределах математики, редко появляясь в повседневной речи. Поэтому менее привычны слова вычитаемое, уменьшаемое, разность. Правило нахождения каждого из данных компонентов возможно применить лишь при понимании значения этих названий.
Значение терминов
В отличие от многих научных терминов, имеющих греческое, латинское или арабское происхождение, в данном случае используются слова с русскими корнями. Так что понять их значение несложно, а значит легко и запомнить, что каким термином обозначается.
Что такое разность чисел в математике
Если присмотреться к самому названию, становится заметно, что оно имеет отношение к словам «разный», «разница». Из этого можно заключить, что имеется в виду установленная разница между количествами.
Это интересно! Как раскрыть модуль действительного числа и что это такое
Данное понятие в математике означает:
Обратите внимание! Если количества равны друг другу, то между ними нет разницы. Значит разность их равняется нулю.
Что такое уменьшаемое и вычитаемое
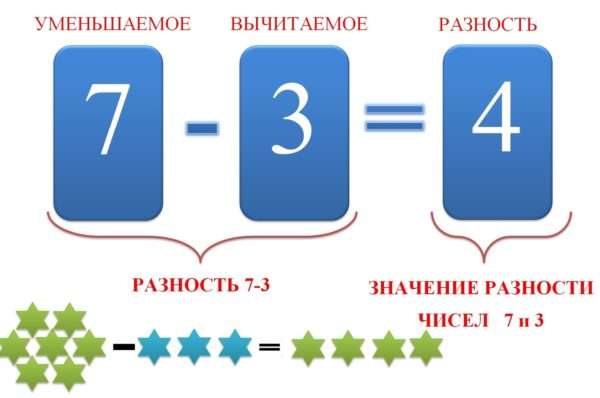
Как следует из названия, уменьшаемое – это то, что делают меньше. А сделать количество меньшим можно, отняв от него часть. Таким образом, уменьшаемым называется число, от которого отнимают часть.
Вычитаемым, соответственно, называется то число, которое от него отнимают.
| Уменьшаемое | Вычитаемое | Разность | |
| 18 | 11 | = | 7 |
| 14 | 5 | = | 9 |
| 26 | 22 | = | 4 |
Полезное видео: уменьшаемое, вычитаемое, разность
Правила нахождения неизвестного элемента
Разобравшись в терминах, несложно установить, по какому правилу находится каждый из элементов вычитания.
Поскольку разность – результат данного арифметического действия, то ее и находят с помощью этого действия, никаких других правил тут не требуется. Но они есть на случай, если неизвестен другой член математического выражения.
Это интересно! Уроки математики: умножение на ноль главное правило
Как найти уменьшаемое
Данным термином, как было выяснено, называют количество, из которого вычли часть. Но если одну вычли, а другая осталась в итоге, следовательно, из этих двух частей число и состоит. Получается, что найти неизвестное уменьшаемое можно, сложив два известных элемента.
Итак, в данном случае, чтобы найти неизвестное, следует выполнить сложение вычитаемого и разности:
| ? | – | 11 | = | 7 |
Искомое находится путем сложения известных элементов:
| 7 | + | 11 | = | 18 |
Так же и во всех подобных случаях:
| ? | – | 5 | = | 9 |
| 9 | + | 5 | = | 14 |
| ? | – | 22 | = | 4 |
| 4 | + | 22 | = | 26 |
Как найти вычитаемое
Если целое состоит из двух частей (в данном случае количеств), то при вычитании одной из них в результате получится вторая. Таким образом, чтобы найти неизвестное вычитаемое, достаточно вместо него вычесть из целого разность.
| 18 | – | ? | = | 7 |
Из примера видно, что от 18 отняли некоторую величину, и осталось 7. Чтобы найти эту величину, надо от 18 отнять 7.
| 18 | – | 7 | = | 11 |
По тому же правилу решаются и другие подобные примеры.
| 14 | – | ? | = | 9 |
| 14 | – | 9 | = | 5 |
| 26 | – | ? | = | 4 |
| 26 | – | 4 | = | 22 |
Таким образом, зная точное значение названий, можно легко догадаться, по какому правилу следует искать каждый неизвестный элемент.
Это интересно! Как разложить на множители квадратный трехчлен: формула
Полезное видео: как найти неизвестное уменьшаемое
Вывод
Четыре основных арифметических действия – та база, на которой основываются все математические вычисления, от простых до самых сложных. Конечно, в наше время, когда люди стремятся перепоручить технике все вплоть до мыслительного процесса, привычнее и быстрее производить вычисления с помощью калькулятора. Но любое умение увеличивает независимость человека – от технических средств, от окружающих. Не обязательно делать математику своей специальностью, но обладать хотя бы минимальными знаниями и умениями – значит иметь дополнительную опору для собственной уверенности.
Частное в математике — определение, свойства и формула
Математика – царица наук. Она хоть и сложна, и многие боятся некоторых запутанных формул и вычислений, но все они состоят из простых арифметических действий сложения, вычитания, умножения и деления.
Производные операции от этих действий называются суммой, разностью, произведением и частным. Что такое частное в математике и каковы его главные свойства – будет подробно рассказано далее.
Основное свойство частного
Деление – это арифметическая операция, обратная умножению. С ее помощью можно просто узнать, сколько в первом числе содержится значений второго.
По аналогии с умножением, которое способно заменить собой многократное сложение, дробление способно заменить многократное вычитание.
Например, необходимо разделить 10 на 2. Это означает, что требуется узнать, сколько раз число 2 содержится в 10. Делая это вычитанием можно получить следующее:
10 — 2 — 2 — 2 — 2 — 2 = 0.
Проводя постепенное вычитание до нуля, можно определить, что двойка содержится в десятке ровно 5 раз и не образует остаток. Сделать это можно было однократно поделив два значения:
Частное чисел – это итог процесса деления одного значения на второе. Пример:
Одно из важнейших правил деления частного, называемое основным свойством частного, заключается в том, что если делимое и делитель умножить или разделить на одно и то же число, то итог этой операции и, соответственно частное, не изменится:
При делении числа самого на себя результатом всегда будет единица, то есть справедливо равенство:
Справедливо и другое правило: если разделить определенную величину на единицу, то итогом процесса будет сама эта величина, то есть делимое:
Увеличение или уменьшение делимого
Некоторые другие соотношения вытекают из этих. Например, если увеличить или уменьшить делимое в n раз, то в результате частное также повысится или понизится в n раз соответственно.
Изложенное правило имеет такой вид:
12 ⁄ 2 = 6 и пусть n = 3.
Проведём увеличение и уменьшение делимого:
(12∗3) /2 = 6∗3 — увеличили делимое на 3, равенство верное: 36 / 2 = 18;
(12 / 3) / 2 = 6 / 3 — уменьшили делимое на 3, равенство все равно верное: 4 / 2 = 2.
То есть, в три раза увеличив делимое, можно в три раза увеличить частное. Аналогично выполняется и уменьшение.
Увеличение или уменьшение делителя
Следующее правило звучит так: если увеличить или уменьшить делитель в n раз, то результат деления понизится или повысится в n-нное количество раз:
Для примера требуется взять частное двух значений 54 и 6:
a / b = c и пусть n = 3.
Проведём увеличение и уменьшение делителя:
54 / (6∗3) = 9 / 3 — увеличили делитель в 3 раза, равенство верное: 54 / 18 =3;
54 / (6 / 3) = 9∗3 — уменьшили делитель в 3 раза, получаем равенство: 54 / 2 = 27.
Увеличив делитель в 3 раза, во столько же раз уменьшили частное. Уменьшив делитель в три раза, делитель, напротив, увеличился в три раза.
Проверить эти «законы» можно в любом онлайн калькуляторе или вручную в уме или на бумаге.
Данные правила являются фундаментальными и составляют базу арифметики, с которой начинается математика и остальные области знаний.
Что такое частное в математике?
Математика – уникальная наука, которая привлекает точностью и последовательностью. Каждый, кто начал изучать эту важную дисциплину, должен разобраться, что такое частное в математике.
Деление
В математике есть четыре простейших операции:
Если мы говорим о частном, то нас будет интересовать такая операция, как деление.
Деление всегда обратно умножению. Это математическая величина, которую мы получим, разделив одно число на другое. Есть ряд символов, которые обозначают его:
В учебных пособиях для учеников 1 – 5 классов есть простое и точное определение этого понятия. Деление – это операция, в результате которой мы получаем число, которое при умножении на делитель дает делимое. Число, о котором говорится в первой части определения, и есть частное.
Частное рассказывает, во сколько раз одно число больше другого.
Наглядные примеры
Чтобы лучше понять, что такое частное чисел в математике, следует обратиться к примерам. Они помогут разложить знания по полочкам в вашей голове. Решение примеров – это лучший тренажер для усвоения новых знаний. Приступим к их решению.
Итак, частное получается, если делимое поделить на делитель. При помощи символов эту операцию можно записать следующим образом:
Запишем простой пример из математики:
80:2=40
80 – делимое (оно делится)
2 – это делитель (на него разделяют)
Восемьдесят больше, чем сорок, в два раза.
Другой пример выглядит так:
120:2=60
Сто двадцать больше, чем шестьдесят, в два раза.
Проверка
Если вы провели операцию деления и сомневаетесь в результате, на помощь придет проверка. Для этого умножьте делитель на частное. Если в результате вы получили делимое, то пример решен верно:
Если после знака равно вы увидели знакомое вам делимое, то можете поставить себе твердую пятерку. Вы научились находить частное чисел и делать проверку. Это очень важно, чтобы в дальнейшем освоить более сложные понятия в алгебре и геометрии.
Частное – это основа математики. Если ученик не смог понять его суть, то двигаться дальше просто бессмысленно. Обратитесь к учителю, если это понятие так и осталось для вас туманным. Педагог разъяснит все ошибки и укажет на подводные камни.
Полное и неполное частное
В результате проведения математических подсчетов частное может быть двух видов:
100:2=50
50 – полное частное
51:2=25 (остаток 1)
25 – неполное частное
1 – остаток от деления
Если вы откроете учебник математики, то увидите, что частное в задачах обозначают при помощи различных символов (переменных). Для этого используют латинские буквы:
30:6=x
Чтобы найти частное, следует делимое разделить на делитель:
Ответ 5 – это частное в данном примере.
Абстрактные определения и туманные рассуждения плохо усваиваются мозгом школьника. Поэтому всегда держите под рукой задачник со списком упражнений по математике. Он поможет понять различные математические категории на практике. Конкретные цифры, записанные в тетради, станут главными помощниками.
Что такое разность и частное
Ответ или решение 2
Определим, что такое разность и что такое частное
Разность и частное относятся к математическим понятиям. Так же, есть такие понятия, как сумма и произведение. Все эти понятия взаимосвязаны с математическими терминами:
Определим понятие разности
Разность – это результат действия вычитания. Разность состоит уменьшаемого, вычитаемого и разности.
Рассмотрим на примере: 9 – 3 = 6, где 9 – уменьшаемое, 3 – вычитаемое, 6 – разность. Для того, чтобы сделать проверку разности, нужно найти сумму вычитаемого и разности.
Рассмотрим примеры разностей:
Определим понятие частного
Частное – это результат действия деления. Частное состоит из делимого, делителя и частного.
Рассмотрим на примере: 15/5 = 3, где 15 – делимое, 5 – делитель, 3 – частное. Для того, чтобы сделать проверку, нужно найти произведение делителя и частного.
Рассмотрим примеры частных:
Свойства суммы, разности, произведения и частного:
Разность мы получаем в результате вычитания одного числа от другого.
Вычислим чему равна разность чисел 10 и 5.
Частное мы получаем у результате деления одного числа на другое.