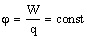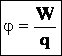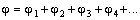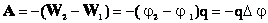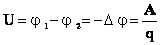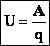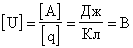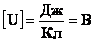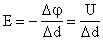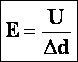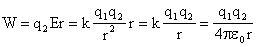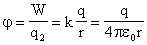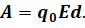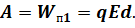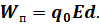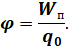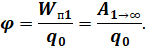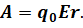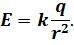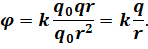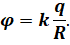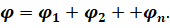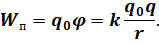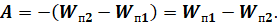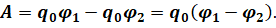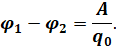Что такое разность потенциалов формула

Разность потенциалов

Поскольку электрический ток является упорядоченным движением заряженных частиц, то для определения величины тока необходимо знать, как величину энергии частиц, так и силу стороннего воздействия на них.

Сущность понятия потенциальной разницы

Для изучения свойств заряженных частиц, помещенных в электростатическое поле, введено понятие потенциала. Оно означает отношение энергии заряда, помещенного в электростатическое поле, к его величине.

При переносе заряженной частицы в другую точку поля меняется его потенциальная энергия, а величина заряда остается неизменной. Для переноса требуется затратить некоторое количество энергии. Данная энергия по переносу единицы заряда получила название электрического напряжения. Соответственно, больший запас энергии будет ускорять перенос, то есть, чем больше напряжение, тем больше ток в цепи.

В данном случае разность потенциалов – это численное равенство напряжению между точками нахождения единичного заряда. Для общего случая здесь должна добавляться работа сторонних сил, которая называется электродвижущей силой (ЭДС). По своей сути, электричество – это работа стороннего источника (генератора) по поддержанию в электросхеме заданных уровней напряжения и тока.

Единица разности потенциалов

В честь ученого (Алессандро Вольта), впервые доказавшего существование разницы потенциалов, единица измерения названа Вольт. В международной системе единиц напряжение обозначается символами:

Кроме этого, существуют кратные обозначения:

Поток вектора магнитной индукции

Электростатическое поле характеризуется напряженностью, которая вместе с вектором электромагнитной индукции составляет электромагнитное поле.

Если заряженная частица движется в электромагнитном поле, то полную силу, которая воздействует на частицу, определяют по закону Лоренца:

Обратите внимание! В указанной формуле приведены векторные величины. Крестом обозначено векторное произведение.

Силу F воздействия на частицу принято называть силой Лоренца.

Данная формула является наиболее общей и может использоваться для вычисления при условии точечного заряда (в том числе единичного).

Теорема Гаусса для магнитного поля

Теорема Гаусса является одной из самых основных в электродинамике законов. Существуют теоремы Гаусса для электрического и магнитного полей, которые входят в состав уравнений Максвелла. При помощи данного закона устанавливается связь между напряженностью электрического поля и заряда в случае произвольной поверхности. Теорема (закон) Гаусса гласит, что в произвольной замкнутой поверхности поток вектора электрического поля пропорционален заряду, заключенному внутри поверхности. Для магнитного поля теорема Гаусса говорит о том, что поток вектора магнитной индукции через произвольную замкнутую поверхность равен нулю.

Выражение для потенциала поля точечного заряда

Поскольку потенциал равен интегралу от напряженности поля, то можно подставить под знак интеграла выражение для напряженности поля единичного заряда. После интегрирования и преобразования выражение для поля точечного заряда принимает вид:

Приведенное выражение свидетельствует, что величина энергии растет пропорционально степени заряженности и падает пропорционально расстоянию.

Проводники в электростатическом поле

Размещение проводника в электростатическом поле приводит к тому, что поле начнет действовать на носители заряда внутри проводящего предмета. Носители начинают перемещаться до тех пор, пока электростатическое поле вне поверхности ни обратится в нуль.

Поскольку поле внутри вещества отсутствует, то во всех точках проводящего материала энергия будет постоянной, а поверхность эквипотенциальной. Векторы напряженности поля направлены под прямым углом в любой точке поверхности проводника.

Под действием поля заряды внутри проводника отсутствуют, поскольку они сосредоточены исключительно на поверхности. Этот факт используется при экранировке – защите тел от влияния внешних электромагнитных и электростатических полей. Для экранирования может использоваться не только сплошной проводящий материал, но и сетка, так называемая «клетка Фарадея».

Также свойство перемещения заряженных частиц (электронов) используется в электростатических генераторах для получения напряжения в несколько миллионов вольт.

Электроемкость уединенного проводника

Для связи величин заряда и напряжения введено понятие электрической емкости. Для уединенного проводника (такого, на который отсутствует влияние других заряженных тел) значение емкости – величина постоянная и равная отношению количества заряда к потенциалу. Другими словами, емкость показывает, какой заряд нужно сообщить проводнику, чтобы его потенциальная энергия увеличилась на единицу.

Электроемкость не зависит от степени заряженности. Роль играют только:

Так же, как и емкость электрического конденсатора, электроемкость проводника будет обозначаться в фарадах.

Обратите внимание! На практике электроемкость проводника составляет очень малую величину. Для увеличения значения, особенно при производстве конденсаторов, как элементов с нормированным значением емкости, разработаны особые технологии.

Падение потенциала вдоль проводника

На концах проводника, помещенного в электрическое поле, начинает наблюдаться разность потенциалов. Вследствие этого электроны начинают перемещаться в сторону увеличения разности. В проводнике возникает электрический ток. Свободные электроны продвигаются вдоль проводника до тех пор, пока разница ни будет равна нулю. На практике для поддержания заданной величины тока цепи запитываются от источников напряжения или тока. Разница заключается в следующем:

Разница потенциалов (падение напряжения) пропорциональна расстоянию от концов проводника, то есть обладает линейной зависимостью.

Опыт Вольта

Первым доказал существование разности потенциалов Алессандро Вольта. Для опытов были взяты два диска, выполненных из меди и цинка и насаженных на стержень электроскопа. При соприкосновении меди и цинка листочки электроскопа расходятся, свидетельствуя о наличии электрического заряда.

На основании своих опытов ученый изготовил первый источник электрического напряжения – вольтов столб.

Измерение контактной разности потенциалов

Основная проблема заключатся в том, что контактная разность потенциалов не может быть измерена напрямую, вольтметром, хотя значение ЭДС в цепи с соединением двух различных проводников может составлять от долей до единиц вольт.

Контактная потенциальная разница существенно влияет на вольтамперную характеристику измеряемой цепи. Наглядным примером может служить полупроводниковый диод, где подобное явление возникает на границе соприкосновения полупроводников с разным типом проводимости.

Разность потенциалов на практике

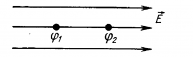
С общепринятой точки зрения, разность потенциалов – это напряжение между двумя выбранными точками цепи. В то же время напряжение между каждой из этих точек и третьей точкой будет отличаться в полном соответствии с определением.

Наглядный пример:

Необходимо найти напряжение между точками А и В.

В данном случае искомая разность составляет:

Рассматриваемые понятия важны для минимального объема знаний в области электротехники и электроники, поскольку на них основываются все расчеты и практические решения. Без этих азов невозможно более углубленное изучение электрических дисциплин.

Видео

Источник

Потенциал. Разность потенциалов. Напряжение.Эквипотенциальные поверхности

Потенциал. Разность потенциалов. Напряжение.

Потенциал электростатического поля — скалярная величина, равная отношению потен­циальной энергии заряда в поле к этому заряду:

— энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле.

Т.к. потенциальная энергия зависит от выбора системы координат, то и потенциал определяется с точностью до постоянной.

За точку отсчета потенциала выбирают в зависимости от задачи: а) потенциал Земли, б) потенциал бесконечно удаленной точки поля, в) потенциал отрицательной пластины конденсатора.

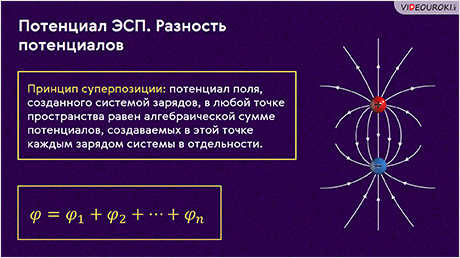
— следствие принци­па суперпозиции полей (потенциалы складываютсяалгебраически).

Потенциал численно равен работе поля по перемещению единичного положительного заряда из данной точки электрического поля в бесконечность.

В СИ потенциал измеряется в вольтах:

Разность потенциалов

Напряжение — разность значений потенциала в начальной и конечнойточках траектории.

Напряжение численно равно работе электростатического поля при перемещении единичного положительного заряда вдоль силовых линий этого поля.

Разность потенциалов (напряжение) не зависит от выбора

Единица разности потенциалов

Напряжение равно 1 В, если при перемещении положительного заряда в 1 Кл вдоль силовых линий поле совершает работу в 1 Дж.

Связь между напряженностью и напряжением.

Из доказанного выше: →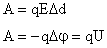

напряженность равна градиенту потенциала (скорости изменения потенциала вдоль направления d).

Из этого соотношения видно:

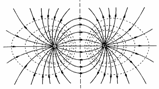
Эквипотенциальные поверхности.

— работа при перемещении заряда вдоль эквипотенциальной поверхности не совершается;

— вектор напряженности перпендикулярен к ЭПП в каждой ее точке.

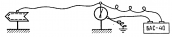
Измерение электрического напряжения (разности потенциалов)

Между стержнем и корпусом — электрическое поле. Измерение потенциала кондуктора Измерение напряжения на гальваническом элементе Электрометр дает большую точность, чем вольтметр.

Потенциальная энергия взаимодействия зарядов.

Потенциал поля точечного заряда

Потенциал заряженного шара

а) Внутри шара Е=0, следовательно, потенциалы во всех точках внутри заряженного металлического шара одинаковы (. ) и равны потенциалу на поверхности шара.

б) Снаружи поле шара убывает обратно пропорционально расстоянию от центра шара, как и в случае точечного заряда.

Перераспределение зарядов при контакте заряженных проводников.

Переход зарядов происходит до тех пор, пока потенциалы контактирующих тел не станут равными.

Источник

Потенциал. Разность потенциалов.

Разность потенциалов (напряжение) между 2-мя точками поля равняется отношению работы поля по перемещению заряда из начальной точки в конечную к этому заряду:

,

Так как работа по перемещению заряда в потенциальном поле не зависит от формы траектории, то, зная напряжение между двумя точками, мы определим работу, которая совершается полем по перемещению единичного заряда.

Если есть несколько точечных зарядов, значит, потенциал поля в некоторой точке пространс­тва определяется как алгебраическая сумма потенциалов электрических полей каждого заряда в данной точке:

.

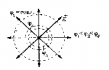
Эквипотенциальной поверхностью, или поверхностью равного потенциала, является поверхность, для любых точек которой разность потенциалов равна нулю. Это означяет, что работа по перемещению заряда по такой поверхности равна нулю, следовательно, линии напряженности электрического поля перпендикулярны эквипотенциальным поверхностям. Эквипотенциальные поверхности однородного поля представляют собой плоскости, а точечного заряда — концентрические сферы.

Вектор напряженности (как и сила ) перпендикулярен эквипотенциальным поверхнос­тям. Эквипотенциальной является поверхность любого проводника в электростатическом поле, так как силовые линии перпендикулярны поверхности проводника. Внутри проводника разность потенциалов между любыми его точками равна нулю.

В однородном электрическом поле напряженность E в каждой точке одинакова, и работа A по перемещению заряда q параллельно на расстояние d между двумя точками с потенциалами φ₁, и φ₂ равна:

,

.

Т.о., напряженность поля пропорциональна разности потенциалов и направлена в сторону уменьшения потенциала. Поэтому положительный заряд будет двигаться в сторону уменьшения потенциала, а отрицательный — в сторону его увеличения.

Единицей напряжения (разности потенциалов) является вольт. Исходя из формулы , , разность потенциалов между двумя точками равна одному вольту, если при перемещении заряда в 1 Кл между этими точками поле совершает работу в 1 Дж.

Источник

Что такое потенциал, какой его смысл? И что такое разность потенциалов?

Если вы ведете речь о потенциале, как о разновидности электрической величины и как о характеристике, определяющей функцию напряжения, то это мера количества энергии. Все предметы вокруг нас состоят из атомов, молекул, электронов и других частиц, которые постоянно взаимодействуют между собой посредством электромагнитных сил. Потенциал представляет собой количественное выражение той самой энергии, которая возникает при взаимодействии мельчайших частиц. Но, в отсутствии пути передачи этой энергии она будет находиться в одной точке или на одном объекте.

Если рассмотреть суть электрического потенциала не с электрической стороны, а на более понятном примере, можете представить себе рогатку, в которую вы заряжаете шарик. Если оттянуть резинку на полметра и зафиксировать шар в этом положении, то он получит количество энергии, которая при освобождении запустит шар на 10 метров. Если тот же шар в резинке отвести на метр и зафиксировать в таком положении, то он будет обладать потенциалом энергии, которая сможет запустить его на 20 метров. Так вот потенциал представляет собой невидимую энергию, которая до возникновения определенных условий не может реализоваться или расходоваться.

Под разностью потенциалов понимается ситуация, когда в двух точках присутствует разное количество энергии. Классическим вариантом разности потенциалов является пальчиковая батарейка, на концах которой присутствует разность потенциалов в 1,5В – это означает, что потенциал плюсового полюса больше потенциала минусового полюса на 1,5В. Если рассмотреть напряжение в розетке, то разность потенциалов в ней составит 220В, но в отличии от батарейки, величина потенциала в каждой точке постоянно меняется, однако их разность остается постоянной – 220В.

Источник

Потенциал электростатического поля. Разность потенциалов

Урок 47. Физика 10 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Потенциал электростатического поля. Разность потенциалов»

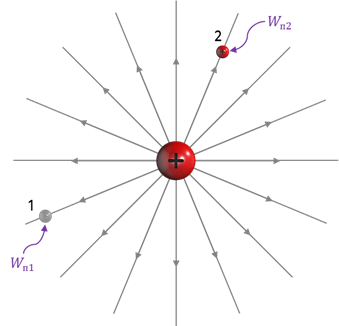
На прошлом уроке мы с вами говорили о том, что на помещённый в электростатическое поле пробный заряд, будет действовать сила, под действием которой заряд способен перемещаться вдоль линии напряжённости поля. Иными словами, электростатическое поле способно совершать работу, значение которой пропорционально величине переносимого заряда и зависит только от того, из какой и в какую точку поля заряд переносится:

При этом на замкнутой траектории работа сил электростатического поля равна нулю.

Напомним, что если работа сил поля не зависит от формы траектории и на замкнутой траектории равна нулю, то такое поле называется потенциальными. Следовательно, точечный заряд, находящийся в любой точке электростатического поля, обладает потенциальной энергией взаимодействия с этим полем, значение которой определяют относительно произвольно выбираемой нулевой точки (чаще всего, это бесконечно удалённая точка поля). В нулевой точке потенциальную энергию заряда в поле принимают равной нулю. Тогда потенциальная энергия взаимодействия точечного заряда с электростатическим полем равна работе, которую совершили бы силы поля при перемещении данного заряда из указанной точки поля в нулевую точку:

Из этого определения следует, что величина потенциальной энергии заряда в электростатическом поле пропорционально значению этого заряда:

Иными словами, если мы будем вносить в одну и туже точку электростатического поля пробные заряды, значения которых будут отличаться в два, три, четыре и так далее раз, то потенциальные энергии этих зарядов будут отличаться во столько же раз.

Однако, отношение потенциальной энергии пробного заряда в поле к значению этого заряда для данной точки поля остаётся неизменным:

Отношение потенциальной энергии пробного заряда, помещённого в данную точку поля, к величине этого заряда, называется потенциалом электростатического поля в данной точке пространства:

Обозначать потенциал мы будем греческой буквой «Фи» (φ).

Вы уже знаете, что силовой характеристикой электрического поля является напряжённость. Потенциал же характеризует энергетическое состояние поля в данной точке пространства.

Поскольку потенциальная энергия заряда в электростатическом поле зависит от выбора нулевой точки, то эта зависимость сохраняется и для потенциала. Если принять, что на бесконечно большом расстоянии от источника поле отсутствует, то потенциал поля в данной точке численно равен работе, совершаемой при перемещении пробного заряда из данной точки поля в бесконечность (то есть в нулевую точку):

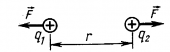
Найдём формулу, по которой можно рассчитать потенциал электростатического поля, создаваемого точечным зарядом, на некотором расстоянии от него. Для этого запишем формулу для определения работы электростатического поля:

Здесь r — это расстояние от создающего поле заряда до исследуемой точки поля. А модуль напряжённости поля прямо пропорционален модулю этого заряда и обратно пропорционален квадрату расстояния между зарядом и точкой, в которой определяют значение напряжённости:

Перепишем формулу для потенциала поля с учётом наших рассуждений.

После упрощения, получим формулу, по которой можно рассчитать потенциал электростатического поля точечного заряда на заданном расстоянии от него. Из формулы видно, что знак заряда-источника поля определяет знак потенциала этого поля.

По этой же формуле можно рассчитывать и потенциал поля, создаваемого равномерно заряженной проводящей сферой в точках, находящихся вне сферы. Для точек же, находящихся на поверхности и внутри сферы, в знаменателе формулы «Эр малое» заменяется на радиус сферы:

Если электростатическое поле создаётся системой зарядов, то имеет место принцип суперпозиции: потенциал такого поля в любой точке пространства равен алгебраической сумме потенциалов, создаваемых в этой точке каждым зарядом системы в отдельности:

Зная потенциал поля в данной точке, можно рассчитать потенциальную энергию заряда, помещённого в эту точку:

На прошлом уроке мы с вами отмечали тот факт, что работа сил электростатического поля по перемещению электрического заряда из начальной точки в конечную равна изменению потенциальной энергии, взятому с обратным знаком:

Давайте выразим потенциальную энергию через потенциалы поля в соответствующих точках:

Подставим значения потенциальных энергий в формулу для работы.

Как видно из полученной формулы, работа поля по перемещению заряда из одной его точки в другую пропорциональна значению переносимого заряда и разности потенциалов начальной и конечной точек.

А теперь давайте разделим выражение для работы на величину переносимого заряда q₀:

Скалярная физическая величина, численно равная отношению работы сил поля по перемещению заряда между данными точками поля к величине этого заряда, называется разностью потенциалов.

Как и изменение потенциальной энергии, разность потенциалов не зависит от выбора нулевой точки.

Из определения следует, что единицей разности потенциалов в СИ является Дж/Кл. Эта единица называется вольтом, в честь итальянского учёного Алессандро Джузеппе Антонио Анастасио Джероламо Умберто Вольта.

1 В — это разность потенциалов между двумя такими точками электростатического поля, при перемещении между которыми заряда в 1 Кл силами поля совершается работа 1 Дж.

Как вы, наверное, догадались, разность потенциалов очень часто называют напряжением.

То есть напряжение между двумя точками поля определяется работой сил этого поля по перемещению заряда 1 Кл из одной точки в другую. В электростатическом поле напряжение вдоль замкнутого контура всегда равно нулю.

Для закрепления нового материала, решим с вами несколько задач. Задача 1. В центре проводящей сферы с равномерно распределённым положительным зарядом в 45 нКл находится металлический шарик с отрицательным зарядом, модуль которого равен 17 нКл. Определите потенциал электростатического поля в точке, находящейся вне сферы на расстоянии 30 м от её центра.

Задача 2. Электрон влетает в однородное электростатическое поле по направлению силовой линии. Определите потенциал точки поля, в которой электрон поменяет направление движения, если в точке поля с потенциалом 1 В его скорость равнялась 300 км/с.

Источник