Что такое разрядность числа
Разряды и классы чисел по математике — что это?
В начальных классах дети изучают «Разряды и классы чисел», однако эта тема вызывает много вопросов у родителей.
В этой статье Вы сможете «освежить» свои знания и объяснить ребенку эту тему.
Числа и цифры
ЧИСЛА — это единицы счёта. С помощью чисел можно сосчитать количество предметов и определить различные величины (длину, ширину, высоту и т. д.).
Для записи чисел используются специальные знаки — ЦИФРЫ.
Цифр десять: 1 2 3 4 5 6 7 8 9 0
Натуральные числа
НАТУРАЛЬНЫЕ ЧИСЛА — это числа, которые используются при счёте.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …,
1 — самое маленькое число, а самого большого числа не существует.
Число 0 (нуль) обозначает отсутствие предмета. Нуль НЕ является натуральным числом.
Разряды и классы натуральных чисел
Для записи чисел используется ДЕСЯТИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ. В десятичной системе счисления пользуются единицами, десятками единиц, десятками десятков — сотнями и т. д.
Каждая новая единица счёта больше предыдущей ровно в 10 раз:
Десятичная система счисления — позиционная. В этой системе счисления значение каждой цифры в записи числа зависит от её позиции (места).
Позиция (место) цифры в записи числа называется РАЗРЯДОМ. Самый младший разряд — ЕДИНИЦЫ. Затем следуют ДЕСЯТКИ, СОТНИ, ТЫСЯЧИ и т. д.
Каждые три разряда натуральных чисел образуют КЛАСС.

Основной вопрос, который родители часто задают: зачем ребенку эти знания? Ответ на этот вопрос очень простой — после изучения этого материала, дети переходят к таким темам как сложение и вычитание в столбик, где обязательно необходимо знать разряды числа, чтобы правильно вычислить примеры.
И если ребенок не освоит эту тему, тогда он не сможет правильно решать в столбик.
Складываем и вычитаем через разряды
Сложение столбиком

Записываем под единицами.
Б) Складываем десятки: 4 + 3 = 7.
Записываем под десятками.
В) Складываем сотни: 4 + 3 = 7.
Записываем под сотнями.
Ответ: 777
Вычитание столбиком

Записываем под единицами.
Б) Вычитаем десятки: 0 меньше,
чем 2, занимаем в сотнях (тысячах).
10 – 2 = 8. Записываем под десятками.
В) Вычитаем сотни: 9 – 4 = 5.
Записываем под сотнями.
Ответ: 586
Как научить ребенка читать по слогам?
У каждого родителя наступает момент следующей ступени развития его ребёнка. Поэтому, многие задаются вопросом: «Как же мне научить читать своего ребёнка?!» Читать далее
Почему дети говорят обидные слова?
В статье рассказывается о том, почему дети произносят обидные слова в сторону родителей, что с этим делать. Читать далее
Как воспитать вундеркинда?
В статье речь пойдет о нескольких этапах становления ребенка-вундеркинда и о роли мам и пап в этом процессе. Читать далее
Все ли дети талантливы?
Родители пытаются воспитать из своих детей каких-то супер героев, такая модная тенденция 21 века. Но все ли дети талантливы? Читать далее
Какие школьные принадлежности опасны для здоровья ребенка
В статье будет рассказано о том, на что нужно делать акцент при покупке принадлежностей, а что лучше не трогать. Читать далее
Старшие и младшие разряды чисел
Чисто технически было бы очень сложно сделать компьютер, который бы «понимал» десятичные числа. А вот сделать компьютер, который понимает двоичные числа достаточно легко. Двоичное число оперирует только двумя цифрами – 0 и 1. Несложно сопоставить с этими цифрами два состояния – вЫключено и включено (или нет напряжения – есть напряжение). Процессор – это микросхема с множеством выводов. Если принять, что отсутствие напряжения на выводе – это 0 (ноль), а наличие напряжения на выводе – это 1 (единица), то каждый вывод может работать с одной двоичной цифрой. Сейчас мы говорим о процессоре очень упрощённо, потому что мы изучаем не процессоры, а системы исчисления. Об устройстве процессора вы можете почитать здесь: Структура процессора.
Конечно, это касается не только процессоров, но и других составляющих компьютера, например, шины данных или шины адреса. И когда мы говорим, например, о разрядности шины данных, мы имеем ввиду количество выводов на шине данных, по которым передаются данные, то есть о количестве двоичных цифр в числе, которое может быть передано по шине данных за один раз. Но о разрядности чуть позже.
Итак, процессор (и компьютер в целом) использует двоичную систему, которая оперирует всего двумя цифрами: 0 и 1. И поэтому основание двоичной системы равно 2. Аналогично, основание десятичной системы равно 10, так как там используются 10 цифр.
Каждая цифра в двоичном числе называется бит (или разряд). Четыре бита – это полубайт (или тетрада), 8 бит – байт, 16 бит – слово, 32 бита – двойное слово. Запомните эти термины, потому что в программировании они используются очень часто. Возможно, вам уже приходилось слышать фразы типа слово данных или байт данных. Теперь, я надеюсь, вы понимаете, что это такое.
Отсчёт битов в числе начинается с нуля и справа. То есть в двоичном числе самый младший бит (нулевой бит) является крайним справа. Слева находится старший бит. Например, в слове старший бит – это 15-й бит, а в байте – 7-й. В конец двоичного числа принято добавлять букву b. Таким образом вы (и ассемблер) будете знать, что это двоичное число. Например, А теперь попробуем понять, как формируется двоичное число.
Ноль, он и в Африке ноль. Здесь вопросов нет. Но что дальше. А дальше разряды двоичного числа заполняются по мере увеличения этого числа. Для примера рассмотрим тетраду. Тетрада (или полубайт) имеет 4 бита.
| Двоичное | Десятичное | Пояснения |
| 0000 | – | |
| 0001 | 1 | В младший бит устанавливается 1. |
| 0010 | 2 | В следующий бит (бит 1) устанавливается 1, предыдущий бит (бит 0) очищается. |
| 0011 | 3 | В младший бит устанавливается 1. |
| 0100 | 4 | В следующий бит (бит 2) устанавливается 1, младшие биты (бит 0 и 1) очищаются. |
| 0101 | 5 | В младший бит устанавливается 1. |
| 0110 | 6 | Продолжаем в том же духе. |
| 0111 | 7 | . |
| 1000 | 8 | . |
| 1001 | 9 | . |
| 1010 | 10 | . |
| 1011 | 11 | . |
| 1100 | 12 | . |
| 1101 | 13 | . |
| 1110 | 14 | . |
| 1111 | 15 | . |
Итак, мы видим, что при формировании двоичных чисел разряды числа заполняются нулями и единицами в определённой последовательности:
Если младший равен нулю, то мы записываем туда единицу. Если в младшем бите единица, то мы переносим её в старший бит, а младший бит очищаем. Тот же принцип действует и в десятичной системе: Всего для тетрады у нас получилось 16 комбинаций. То есть в тетраду можно записать 16 чисел от 0 до 15. Байт – это уже 256 комбинаций и числа от 0 до 255. Ну и так далее. На рис. 2.2 показано наглядно представление двоичного числа (двойное слово).
Мы поможем найти Вам клиентов!
Самый младший двоичный разряд и самый старший двоичный разряд
Нужны новые клиенты? Тогда Вам рекомендуем посмотреть этот раздел нашего сайта
_____
Самый младший двоичный разряд и самый старший двоичный разряд
Системой счисления, которую привыкли использовать большинство людей, является десятичной системой. Мы используем десять цифр 0-1-2-3-4-5-6-7-8-9, и увеличиваем значение степени 10. Возможно, первые люди считали на пальцах; иначе мы могли бы использовать и систему счисления с основанием 6 или 17. Таким образом, основание числа очень важно в любой системе счисления, это положения цифры, которое соответствует степени основания. Когда мы считаем от 0 до 10, мы получаем 1 в позиции десяток и 0 ноль в позиции единиц. Продолжая считать до 100, размешаем 1 в позицию сотен, и 0 в позиции десятков и единиц. Это то, что называется позиционной системой счисления.
В двоичном числе, самая правая цифра представляет собой самый младший двоичный разряд (least significant bit (LSB)), а самая левая цифра – самый старший двоичный разряд (most significant bit (MSB)). Значение разряда любой цифры между этими двумя, младшим и старшим, разрядами, зависит от положения между LSB и MSB.
СИСТЕМА СЧИСЛЕНИЯ С ОСНОВАНИЕМ 2
Знание системы счисления с основанием 2 важно, потому что протокол IP version 4 (IPv4) использует адреса, состоящие из 32 битов. 32 бита разделены на 4 группы по 8 бит, называемых октетами. Для разделения их используется точка, расположенная между октетами. (Другое название для 8 бит это байт, но в этом модуле будет использоваться название октет).
Разряд (позиция, место) — это структурный элемент представления чисел в позиционных системах счисления.
Разряд является «рабочим местом» цифры в числе. Порядковому номеру разряда соответствует его вес — множитель, на который надо умножить значение разряда в данной системе счисления.
Диапазон значений для всех разрядов (в данной системе счисления) неизменен.
Содержание
Определение [ править | править код ]
соответствует представлению z в виде суммы
Пример [ править | править код ]
то есть, цифра в нулевом разряде (справа, начиная с нуля) умножается на 10 в нулевой степени. Цифра в первом разряде — на 10 в первой степени, и т. д.
Первые разряды [ править | править код ]
единицы – от 0 до 9, десятки – от 10 до 99, сотни – от 100 до 999, тысячи – от 1000 до 9999, десятки тысяч – от 10000 до 99999, сотни тысяч – от 100000 до 999999, миллионы – от 1 000 000, миллиарды – от 1 000 000 000,
триллионы – от 1 000 000 000 000, далее идут – квадриллион, квинтиллион, секстиллион, септиллион, октиллион и т. д.
Что такое разрядность числа
Система счисления – это способ записи чисел. Обычно, числа записываются с помощью специальных знаков – цифр (хотя и не всегда). Если вы никогда не изучали данный вопрос, то, по крайней мере, вам должны быть известны две системы счисления – это арабская и римская. В первой используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и это позиционная система счисления. А во второй – I, V, X, L, C, D, M и это непозиционная система счисления.
В позиционных системах счисления количество, обозначаемое цифрой в числе, зависит от ее позиции, а в непозиционных – нет. Например:
11 – здесь первая единица обозначает десять, а вторая – 1.
II – здесь обе единицы обозначают единицу.
345, 259, 521 – здесь цифра 5 в первом случае обозначает 5, во втором – 50, а в третьем – 500.
XXV, XVI, VII – здесь, где бы ни стояла цифра V, она везде обозначает пять единиц. Другими словами, величина, обозначаемая знаком V, не зависит от его позиции.
Сложение, умножение и другие математические операции в позиционных системах счисления выполнить легче, чем в непозиционных, т.к. математические операции осуществляются по несложным алгоритмам (например, умножение в столбик, сравнение двух чисел).
В мире наиболее распространены позиционные системы счисления. Помимо знакомой всем с детства десятичной (где используется десять цифр от 0 до 9), в технике широкое распространение нашли такие системы счисление как двоичная (используются цифры 0 и 1), восьмеричная и шестнадцатеричная.
Следует отметить, важную роль нуля. «Открытие» этой цифры в истории человечества сыграло большую роль в формировании позиционных систем счисления.
Основание системы счисления – это количество знаков, которое используется для записи цифр.
Итак, в позиционной системе счисления числа записываются таким образом, что каждый следующий (движение справа на лево) разряд больше другого на степень основания системы счисления. (придумать схему)
Одно и тоже число (значение) можно представить в различных системах счисления. Представление числа при этом различно, а значение остается неизменным.
Двоичная система счисления
В двоичной системе счисления используются всего две цифры 0 и 1. Другими словами, двойка является основанием двоичной системы счисления. (Аналогично у десятичной системы основание 10.)
Чтобы научиться понимать числа в двоичной системе счисления, сначала рассмотрим, как формируются числа в привычной для нас десятичной системе счисления.
В десятичной системе счисления мы располагаем десятью знаками-цифрами (от 0 до 9). Когда счет достигает 9, то вводится новый разряд (десятки), а единицы обнуляются и счет начинается снова. После 19 разряд десятков увеличивается на 1, а единицы снова обнуляются. И так далее. Когда десятки доходят до 9, то потом появляется третий разряд – сотни.
Двоичная система счисления аналогична десятичной за исключением того, что в формировании числа участвуют всего лишь две знака-цифры: 0 и 1. Как только разряд достигает своего предела (т.е. единицы), появляется новый разряд, а старый обнуляется.
Попробуем считать в двоичной системе:
0 – это ноль
1 – это один (и это предел разряда)
10 – это два
11 – это три (и это снова предел)
100 – это четыре
101 – пять
110 – шесть
111 – семь и т.д.
Перевод чисел из двоичной системы счисления в десятичную
Не трудно заметить, что в двоичной системе счисления длины чисел с увеличением значения растут быстрыми темпами. Как определить, что значит вот это: 10001001? Непривычный к такой форме записи чисел человеческий мозг обычно не может понять сколько это. Неплохо бы уметь переводить двоичные числа в десятичные.
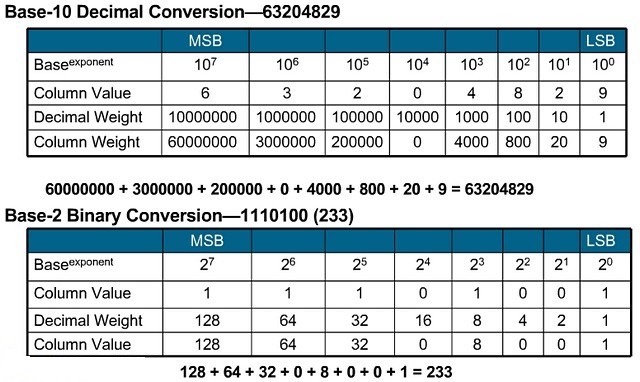
В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и т.д. Например:
1476 = 1000 + 400 + 70 + 6
Можно пойти еще дальше и разложить так:
1476 = 1 * 103 + 4 * 102 + 7 * 101 + 6 * 100
Аналогично можно разложить и любое двоичное число. Только основание здесь будет 2:
10001001 = 1*2 7 + 0*2 6 + 0*2 5 + 0*2 4 + 1*2 3 + 0*2 2 + 0*2 1 + 1*2 0
Если посчитать сумму составляющих, то в итоге мы получим десятичное число, соответствующее 10001001:
1*2 7 + 0*2 6 + 0*2 5 + 0*2 4 + 1*2 3 + 0*2 2 + 0*2 1 + 1*2 0 = 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137
Т.е. число 10001001 по основанию 2 равно числу 137 по основанию 10. Записать это можно так:
100010012 = 13710
Почему двоичная система счисления так распространена?
Дело в том, что двоичная система счисления – это язык вычислительной техники. Каждая цифра должна быть как-то представлена на физическом носителе. Если это десятичная система, то придется создать такое устройство, которое может быть в десяти состояниях. Это сложно. Проще изготовить физический элемент, который может быть лишь в двух состояниях (например, есть ток или нет тока). Это одна из основных причин, почему двоичной системе счисления уделяется столько внимания.
Перевод десятичного числа в двоичное
Может потребоваться перевести десятичное число в двоичное. Один из способов – это деление на два и формирование двоичного числа из остатков. Например, нужно получить из числа 77 его двоичную запись:
77 / 2 = 38 (1 остаток)
38 / 2 = 19 (0 остаток)
19 / 2 = 9 (1 остаток)
9 / 2 = 4 (1 остаток)
4 / 2 = 2 (0 остаток)
2 / 2 = 1 (0 остаток)
1 / 2 = 0 (1 остаток)
Собираем остатки вместе, начиная с конца: 1001101. Это и есть число 77 в двоичном представлении. Проверим:
1001101 = 1*2 6 + 0*2 5 + 0*2 4 + 1*2 3 + 1*2 2 + 0*2 1 + 1*2 0 = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77
Восьмеричная система счисления
Итак, современное «железо понимает» лишь двоичную систему счисления. Однако человеку трудно воспринимать длинные записи нулей и единиц с одной стороны, а с другой – переводит числа из двоичной в десятичную систему и обратно, достаточно долго и трудоемко. В результате, часто программисты используют другие системы счисления: восьмеричную и шестнадцатеричную. И 8 и 16 являются степенями двойки, и преобразовывать двоичное число в них (так же как и выполнять обратную операцию) очень легко.
В восьмеричной системе счисления используется восемь знаков-цифр (от 0 до 7). Каждой цифре соответствуют набор из трех цифр в двоичной системе счисления:
000 – 0
001 – 1
010 – 2
011 – 3
100 – 4
101 – 5
110 – 6
111 – 7
Для преобразования двоичного числа в восьмеричное достаточно разбить его на тройки и заменить их соответствующими им цифрами из восьмеричной системы счисления. Разбивать на тройки нужно начинать с конца, а недостающие цифры в начале заменить нулями. Например:
1011101 = 1 011 101 = 001 011 101 = 1 3 5 = 135
Т.е число 1011101 в двоичной системе счисления равно числу 135 в восьмеричной системе счисления. Или 10111012 = 1358.
Обратный перевод. Допустим, требуется перевести число 1008 (не заблуждайтесь! 100 в восьмеричной системе – это не 100 в десятичной) в двоичную систему счисления.
1008 = 1 0 0 = 001 000 000 = 001000000 = 10000002
Перевод восьмеричного числа в десятичное можно осуществить по уже знакомой схеме:
6728 = 6 * 8 2 + 7 * 8 1 + 2 * 8 0 = 6 * 64 + 56 + 2 = 384 + 56 + 2 = 44210
1008 = 1 * 8 2 + 0 * 8 1 + 0 * 8 0 = 6410
Шестнадцатеричная система счисления
Шестнадцатеричная система счисления, так же как и восьмеричная, широко используется в компьютерной науке из-за легкости перевода в нее двоичных чисел. При шестнадцатеричной записи числа получаются более компактными.
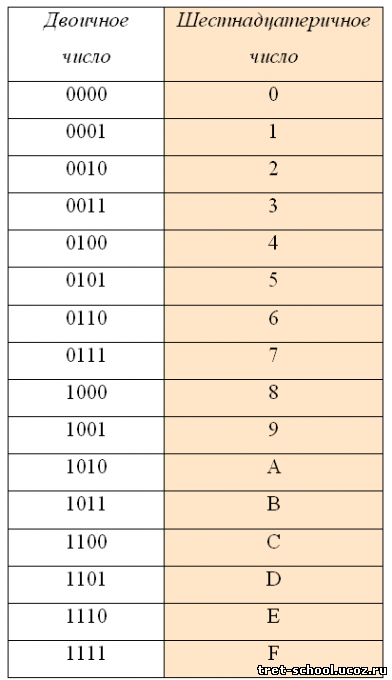
В шестнадцатеричной системе счисления используются цифры от 0 до 9 и шесть первых латинских букв – A (10), B (11), C (12), D (13), E (14), F (15).
При переводе двоичного числа в шестнадцатеричное, первое разбивается на группы по четыре разряда, начиная с конца. В случае, если количество разрядов не делится нацело, то первая четверка дописывается нулями впереди. Каждой четверке соответствует цифра шестнадцатеричной системе счисления:
Например:
10001100101 = 0100 1100 0101 = 4 C 5 = 4C5
Если потребуется, то число 4C5 можно перевести в десятичную систему счисления следующим образом (C следует заменить на соответствующее данному символу число в десятичной системе счисления – это 12):
4C5 = 4 * 162 + 12 * 161 + 5 * 160 = 4 * 256 + 192 + 5 = 1221
FF = 15 * 161 + 15 * 160 = 240 + 15 = 255
255 – это максимальное значение одного байта, равного 8 битам: 1111 1111 = FF. Поэтому с помощью шестнадцатеричной системы счисления очень удобно кратко (с помощью двух цифр-знаков) записывать значения байтов. Внимание! Состояний у 8-ми битного байта может быть 256, однако максимальное значение – 255. Не забывайте про 0 – это как раз 256-е состояние
О разрядности процессоров
Целью данной статьи является попытка посеять сомнение в голове читателя, уверенного, что он знает о разрядности всё или почти всё. Но сомнение должно быть конструктивным, дабы сподвигнуть на собственное исследование и улучшить понимание.
Термин «разрядность» часто используют при описании вычислительных устройств и систем, понимая под этим число бит, одновременно хранимых, обрабатываемых или передаваемых в другое устройство. Но именно применительно к центральным процессорам (ЦП), как к наиболее сложным представителям вычислительного железа, не делимым на отдельные детали (до тех пор, пока кто-то не придумал, как продать отдельно кэш или умножитель внутри чипа), понятие разрядности оказывается весьма расплывчатым. Продемонстрировать это поможет умозрительный пример.
Представьте себе, что вокруг благодатные 80-е, в мире (всё ещё) десятки производителей ЦП, и вы работаете в одном из них над очередным поколением. Никаких 256-битных SSE8, встроенных GPU и 5-канальных контроллёров памяти на свете пока нет, но у вас уже есть готовый 16-битный процессор (точнее, «16-битный» пишется в технической документации), в котором 16 бит везде и во всём — от всех внешних шин до архитектурного размера обрабатываемых данных. Реальным примером такого ЦП могут быть первые однокорпусные (правда, не однокристальные) ЦП для архитектуры DEC PDP-11. И вот приходит задание руководства — разработать новое, обратно совместимое поколение этого же ЦП, которое будет 32-битным — не уточняя, что понимается под последним. Именно это понимание и предстоит прояснить в первую очередь. Итак, наш главный вопрос: что именно надо удвоить по разрядности в нашем пока насквозь 16-битном ЦП, чтобы получившийся процессор мог называться 32-битным? Чтобы решать задачу было легче, применим два подхода: систематизируем определения и посмотрим на примеры.Систематизируем
Первое, что приходит в голову — разрядность чего именно считать? Обратимся к определению любой информационной системы: её три основных функции — это обработка, хранение и ввод-вывод данных, за которые отвечают, соответственно, процессор(ы), память и периферия. Учитывая, что сложная иерархически самоподобная система состоит из многих компонент, можно утверждать, что такое разделение функций сохраняется и на компонентном уровне. Например, тот же процессор в основном обрабатывает данные, но он также обязан их хранить (для чего у него есть относительно небольшая память) и обмениваться с другими компонентами (для этого есть разные шины и их контроллёры). Поэтому будем функционально разделять разрядности обработки, хранения и обмена информации.
Рискну предположить, что все производители любого программируемого «железа», особенно процессоров, на 90% стараются не для конечных пользователей, а для программистов. Следовательно, с точки зрения производителей процессор должен выполнять нужные команды нужным образом. С другой стороны, детали структуры кристалла (топологические, электрические и физические параметры отдельных транзисторов, вентилей, логических элементов и блоков) могут быть скрыты не только от пользователя, но и от программиста. Выходит, что разрядность надо отличать и по реализации — физическую и архитектурную.
Следует добавить, что программисты тоже бывают разные: большинство пишут прикладные программы на языках высокого уровня с помощью компиляторов (что делает код до некоторой степени платформонезависимым), некоторые пишут драйверы и компоненты ОС (что заставляет более внимательно относиться к учёту реальных возможностей аппаратной части), есть творцы на ассемблере (явно требующем знания целевого процессора), а кто-то пишет сами компиляторы и ассемблеры (аналогично). Поэтому под программистами далее будем понимать именно тех, для кого детали аппаратной реализации важны если не для написания программы вообще, то хотя бы для её оптимизации по скорости — «архитектурная» разрядность чего-либо будет относиться именно к программированию на родном машинном языке процессора или более удобном ассемблере, не залезая при этом в нутро ЦП (это уже вопросы микроархитектуры, которую мы для большего различия и назвали физической реализацией). Описанные нюансы всё равно влияют на всех программистов, т.к. языки высокого уровня почти всегда переводятся компиляторами в машинный код, а компиляторы тоже должен кто-то написать. Исключения в виде интерпретируемых языков тоже не стоят в стороне — сами интерпретаторы тоже создаются с помощью компиляторов.
Осталось рассмотреть, разрядность какой именно информации нам интересна. Что вообще потребляет и генерирует ЦП в информационном смысле? Команды, данные, адреса и сигнально-управляющие коды. О последних речь не идёт — их разрядность жёстко зафиксирована в конкретной аппаратной реализации и в большинстве случаев программно не управляема. Чуть трудней с командами — в семействе архитектур RISC, например, разрядность любого обращения к памяти должна быть равна физической разрядности шины данных процессора, в т.ч. и при считывании кода (кроме некоторых послаблений в современных ARM и PowerPC). Это хорошо для ЦП — нет проблем с невыровненным доступом, все команды имеют одинаковую, либо переменную, но просто вычисляемую длину. Зато плохо для программиста — RISC это усечённый набор команд, которые ещё и занимают больше места, чем при более компактном кодировании (для того же алгоритма нужно больше команд, но и для того же числа команд надо больше байтов). Поэтому именно CISC-парадигма завоевала наибольший подход с её разнообразием и переменной длинной команд, не равной разрядности чего-либо. Разумеется, все современные ЦП внутри — настоящие RISC, но это только физически, а не архитектурно. Остались только два вида информации — данные и адреса. Их и рассмотрим.Собираем
У нас имеется три критерия видов разрядности: функциональный (обработки, хранения и обмена), реализационный (физическая и архитектурная) и типовой (данных и адресов). Итого уже 12 видов этой непонятной штуки. Предположим, что на каждую комбинацию критериев для нашего исходного ЦП мы отвечаем «16-битная» (и физическая разрядность обработки данных, и архитектурная хранения адресов, и все остальные). Теперь посмотрим, какие из этих вопросов обязательно должны давать ответ «32-битная», чтобы получившийся процессор оказался именно таким.
Начнём с архитектурной части. Должен ли ЦП хранить данные и адреса в логическом 32-битном формате, чтобы называться 32-битным? Насчёт данных, очевидно, да, а вот по поводу адресов всё не так просто. Почти все 8-битные (по данным) ЦП имеют возможность хранить 16-битные адреса в парах регистров (иначе им не видать распространённой на этих платформах 16-битной адресации), но от этого их не называют 16-битными. Может быть, если ЦП сможет хранить 32-битные данные, но всего-то 16-битные адреса, его уже можно называть 32-битным.
На аналогичные вопросы об архитектурных вычислениях над 32-битными данными и адресами, а также программно 32-битном обмене данных с программно 32-битной адресацией ответ может быть таким же — с данными надо, а с адресами не факт.
Перейдём на физическую реализацию. Должен ли ЦП хранить данные и адреса в физически 32-битном формате? Оказывается, не обязательно, т.к. для 32-битных операндов можно спарить регистры, чем успешно пользовались ещё 8-битные ЦП, начиная с i8080. А зилоговские 16-битные Z8000 могли даже счетверять регистры, получая 64-битный аргумент (только для данных). Это не так эффективно, т.к. полный объём данных, умещающийся в регистровом файле, не увеличится, но это и не требовалось. Зато всегда есть возможность обратиться и к старшей, и к младшей половине виртуального 32-битного регистра — камень в огороды архитектур IA-32 и MC68k, где можно обращаться только к младшей половине (в IA-32 — ещё и с префиксом, что замедляет выполнение).
Идём далее. Должен ли ЦП обрабатывать данные и адреса 32-битными физическими порциями? Оказывается, и это не требуется, операнды можно обрабатывать половинками в функциональных устройствах 16-битного размера. Стоит вспомнить процессор Motorola MC68000, применявшийся в первых Макинтошах, Амигах, Атари и других популярных машинах — он считался 32-битным, в нём есть 32-битные регистры, но нет ни одного 32-битного ФУ (оно появилось только в 68020). Зато есть целых три 16-битных АЛУ, два из которых умеют спариваться при выполнении 32-битной операции. У i8080 и Z80 8-битные АЛУ выполняли 16-битные операции для вычисления адреса последовательно над его байтами. Позже эта история повторилась с набором SSE и его 128-битными операндами, которые поначалу обрабатывались на 64-битных ФУ.
Наконец, обмен: нужно ли процессору физически принимать и передавать данные 32-битными порциями с 32-битной адресацией? На первый вопрос дали ответ почти все производители ЦП, выпустив чипы с половинной шириной шины: 8 бит для 16-битного i8088, 16 бит для 32-битных MC68000/010 и i80386SX/EX/CX, и даже 8 бит для 32-битного MC68008. С физической разрядностью шины адреса куда веселее. Начнём с того, что для многобайтовых шин данных (т.е. начиная с 16-битной) физическая адресация памяти может происходить по словам или по байтам. В первом случае на шину адреса всегда подаётся адрес слова, а шина данных считывает или записывает нужную его часть — от отдельного байта до слова целиком. Для обозначения разрядности доступа может применяться отдельная шина байт-маски (в архитектуре x86 такой приём начал применяться со времён i386 — по биту на каждый байт шины данных), либо комбинация управляющих сигналов с младшими битами шины адреса, которые в этом режиме не нужны (для 32-биной шины данных адрес слова нацело делится на 4, а потому младшие 2 бита шины адреса всегда равны нулю) — так было до выхода i386. Случай же адресации байтов возможен лишь при динамической подстройке ширины шины и из широко известных ЦП применялся только в MC68020/030. В результате к сегодняшнему дню используется именно адресация слов вместе с байт-маской, поэтому физическая разрядность шины адреса оказывается меньше её логической ширины на число бит, на единицу меньшее разрядности шины данных в байтах. Из чего следует, что 32-битная физическая шина адреса может быть только при 8-битной шине данных, на что ни один архитектор и инженер в здравом уме не пойдёт по очевидным соображениям.
Но это ещё не всё. Зачем нам вообще 32-битная физическая или логическая адресация? Середина-конец 80-х, на рынке только-только появились мегабитные микросхемы памяти, типичный объём памяти для ПК пока что измеряется сотнями килобайт, но чуть позже — мегабайтами. А 32-битная адресация позволит получить доступ к 4 ГБ физического ОЗУ! Да кому вообще такое может понадобиться в ближайшие лет 20 в персоналках?! Неудивительно, что первые популярные «32-битные» ЦП имели совсем не 32 бита логической ширины шины адреса: MC68000 имел 24 (23 физических + 1 для управления разрядами), а MC68008 — и вовсе 20. Intel 386SX (вышедший на 3 года позже оригинального полностью 32-битного i80386), помимо уполовинивания шины данных, сократил и шину адреса до 24 (23 физических) бит, а его встраиваемые версии 386EX/CX имели 26-битную шину. Более того, первые чипсеты, позволявшие оперировать 32-битными адресами, появились лишь в 90-х, а первые материнские платы, имевшие достаточное число слотов памяти, чтобы набрать >4 ГБ модулями максимального на тот момент размера — лишь в 2000-х. Хотя первые ЦП с 64-битной физической шиной адреса (IBM/Motorola PowerPC 620) появились аж в 1994 г.. Выводим
Итак, физически в процессоре вообще ничего не требуется делать 32-битным. Достаточно лишь архитектурно убедить программиста, что ЦП выполняет 32-битные операции одной командой. И хотя она при отсутствии полноценных внутренних ресурсов неизбежно будет декодироваться в цепочки микрокода для управления 16-битными физическими порциями информации и аппаратными блоками — это уже программиста не волнует. Так что же, достаточно переписать прошивку, переделать декодер и схему управления, и вот наш 16-битный процессор сразу стал 32-битным?
Как известно, любую хорошую идею можно довести до абсурда, и тогда она сама себя дискредитирует. Увеличение разрядности ЦП — не исключение. На этом месте архитектурщик сразу должен задаться вопросом — а зачем всё это? Увеличивать разрядность данных хорошо для ускорения работы с ними (часто требуется обрабатывать значения, не умещающиеся в 16 бит), а адресов — для получения возможности оперировать большими объёмами данных (ограничение в 64 КБ для 16-битной адресации, кое-как ослабленное сегментной моделью IA-16, сковывало программистов уже в середине 80-х). Можно, конечно, сделать страничную адресацию с программно переключаемыми банками (могли же 8-битные ЦП адресовать 1 МБ на популярных дешёвых ПК и игровых приставках), но ценой усложнения программ и замедления доступа к памяти. Аналогично — разве имеет смысл делать 32-битность для данных такой, что она почти не ускоряет производительность по сравнению с обработкой 32-битных чисел на 16-битной платформе под управлением программы, а не микрокода? Таким образом мы только упростим программирование, сэкономив на числе команд, но не получим скачок в скорости. Из чего мы приходим к выводу — увеличение разрядности должно реализовываться так, чтобы оно реально привело к качественному (больше памяти) и количественному (быстрее операции) скачку возможностей архитектуры. «Больше памяти» здесь относится именно к качественному развитию, т.к. многие алгоритмы и приложения вообще откажутся работать при недостатке ОЗУ, в то время как даже медленный процессор всё равно рано или поздно программу выполнит. Виртуальная память с дисковой подкачкой бессмысленна при менее чем 32-битной реализации.
Но означает ли всё это, что в ЦП как можно больше ресурсов, и аппаратных, и архитектурных, должны быть 32-битными, чтобы его можно было бы назвать полноценным 32-битным процессором? Совсем нет. Возьмём тот же MC68000 — у него 32-битная архитектура для данных и адресов и 32-битные регистры, но 16-битные АЛУ и внешняя шина данных и 24-битная физическая внешняя адресация. Тем не менее, недостаточная «32-битность» не мешает ему обгонять появившийся на 3 года позже «16-битный» 80286: на популярном в 1980-е бенчмарке Dhrystones MC68000 на 8 МГц набирает 2100 «попугаев», а 286 на 10 МГц — 1900 (также 16-битный i8088 на 4,77 МГц — 300).
Но всё это нам не поможет ответить на вопрос — что же такое разрядность процессора? В момент, когда мы уже было пришли к некоему заключению, на сцене появляется новый герой — тип данных. Всё вышеизложенное имело отношение лишь к целочисленным вычислениям и их аргументам. Но ведь есть ещё и вещественные. Кроме того, пока что мы оперируем скалярными величинами, но есть ещё и векторные. А ведь, по слухам, Intel намерена встроить вещественный сопроцессор прямо внутрь своего нового 80486 (напомню: на дворе у нас, условно — 80-е годы). С учётом того, что внутреннее физическое и архитектурное представление данных (с адресами FPU не работает) 80-битное — как же тогда называть «четвёрку» — «32/80-битным» процессором? Вернёмся обратно в настоящее — как называть Pentium MMX, который откусил 64 бита от каждого 80-битного скалярного вещественного регистра и назвал их целочисленным векторным регистром? А Pentum Pro/II с 256-битной шиной данных между кэшем L2 и ядром? (Ещё ранее MIPS R4000 и его варианты имели внутренний контроллёр L2 с внешней 128-битной шиной до самого кэша.) А как назвать Pentium III с его 128-битными регистрами XMM, хотя в каждом таком векторе могут пока храниться лишь 32-битные компоненты, а обрабатываться лишь парами в 64-битных ФУ, но не четвёрками? А как воспринимать готовящиеся сейчас для новых архитектур (в частности, Intel Larrabee) команды векторной адресации типа Scatter и Gather, где части векторного регистра воспринимаются как адреса, а не данные, и потому адресация тоже может считаться ххх-битной?
Современный спор о переходе с 32-битной на 64-битную платформу повторяет эту историю с дополнениями, ещё более подсаливающими и так разнообразное по вкусу блюдо. Прежде всего, если посмотреть на темпы удвоения разрядности (что бы под ней не понимали) однокристальных ЦП, то окажется, что переход от первых 4-битных к первым 32-битным произошёл всего за 8 лет — c 1971 г. (i4004) по 1979 г. (MC68000 и куда менее известный NS32016). Следующее удвоение до 64 бит потребовало 10 лет — i860 имел 32-битное целое скалярное АЛУ и 32-битные универсальные регистры со спариванием, но 64-битные FPU и целочисленное векторное ФУ, 64-битные внешние шины и, впервые, внутреннюю 128-битную шину ядро-кэш. А пока 64 бита добрались до ПК — прошло ещё лет 15, хотя 64-битный доступ к памяти (через 64-битную же шину данных, но для «32-битного» процессора) появился уже в первых Pentium в 1993 г.. А дело в том, что для целочисленных скалярных вычислений два главных типа операндов — данные и адреса — пока достаточно было иметь лишь 32-битными. Об избыточности 32-битной адресации для 80-90-х гг. уже сказано, но и жёсткая необходимость в 64-битных целочисленных вычислениях, в отличие от 32-битных, также до сих пор не возникала, да и не просматривается и сейчас. Для целых чисел диапазон от –2·10 9 до 2·10 9 или от 0 до 4·10 9 покрывает подавляющее большинство нужд, а редкие моменты 64-битности вполне удовлетворяются дедовским способом — операциями над частями операндов с переносом, что не так уж сильно медленнее и доступно с первых моментов появления 32-битных архитектур. Дополнительной пикантности добавляет тот факт, что 64-битная арифметика над целыми числами в архитектуре x86 появились ещё до AMD64 и EM64T, причём сразу векторная — начиная с набора SSE2 (2001 г.) существуют команды paddq и psubq для сложения и вычитания целых 64-битных компонентов, а команды 32-битного перемножения для любой архитектуры дают 64-битное число (команды деления, соответственно — его принимают; аналогично для многих 16-битных платформ, включая IA-16).
Разрядности некоторых процессоров для ПК
| Критерий | Разрядность | |||||||||||
| Функциональный | обработки | хранения | обмена | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Реализационный | физич. | архитектурн. | физич. | архитектурн. | физич. | архитектурн. | ||||||
| Типовой (D: данных; A: адресов) | D | A | D | A | D | A | D | A | D | A | D | A |
| i8080/85, Z80 | 8 | 8 | 8-16 | 16 | 8 | 8 | 8-16 | 16 | 8 | 16 | 8-16 | 16 |
| Z8000 | 16 | 16 | 8-64 | 16 | 16 | 16 | 8-64 | 16 | 8-16 | 23 | 8-64 | 23 |
| MC68000/010 (MC68008) | 16 | 16 | 8-32 | 32 | 32 | 32 | 8-32 | 32 | 8-16 (8) | 24 (20) | 8-32 | 32 |
| MC68020/030 | 32 | 32 | 8-32 | 32 | 32 | 32 | 8-32 | 32 | 8-32 | 32 | 8-32 | 32 |
| i8086/186* (i8088/188*) | 16 | 16 | 8-16 | 16 | 16 | 16 | 8-16 | 16 | 8-16 (8) | 20 | 8-16 | 20 |
| i80286 | 16 | 16 | 8-16 | 16 | 16 | 16 | 8-16 | 16 | 8-16 | 24 | 8-16 | 24 |
| i80386DX | 32 | 32 | 8-32 | 32 | 32 | 32 | 8-32 | 32 | 8-32 | 32 | 8-32 | 32 |
| i80386SX (EX/CX) | 32 | 32 | 8-32 | 32 | 32 | 32 | 8-32 | 32 | 8-16 | 24 (26) | 8-32 | 32 |
| i860 | 32/64|64 | 32 | 8-64/64|64 | 32 | 32/64/32 | 32 | 8-64/64/64 | 32 | 64 | 64 | 8-64 | 64 |
| i80486 | 32/80 | 32 | 8-32/80 | 32 | 32/80 | 32 | 8-32/80 | 32 | 32 | 32 | 8-80 | 32 |
| Pentium, K5 (Pentium Pro) | 32/80 | 32 | 8-32/80 | 32 | 32/80 | 32 | 8-32/80 | 32 | 64 | 32 (36) | 8-80 | 32 (51) |
| Pentium MMX (Pentium II) | 32/80|64 | 32 | 8-32/80|64 | 32 | 32/80|64 | 32 | 8-32/80|64 | 32 | 64 | 32 (36) | 8-80 | 32 (51) |
| K6 (K6-2) | 32/80| 64(/64) | 32 | 8-32/80| 64(/64) | 32 | 32/80| 64(/64) | 32 | 8-32/80| 64(/64) | 32 | 64 | 32 | 8-80 | 32 |
| Athlon | 32/80| 64/64 | 32 | 8-32/80| 64/64 | 32 | 32/80| 64/64 | 32 | 8-32/80| 64/64 | 32 | 64 | 36 | 8-80 | 51 |
| Athlon XP | 32/80| 64/64 | 32 | 8-32/80| 64/32-128 | 32 | 32/80|64/128 | 32 | 8-32/80| 64/128 | 32 | 64 | 36 | 8-128 | 51 |
| Pentium III (Pentium 4/M, Core) | 32/80| 64/64 | 32 | 8-32/80| 64(+128)/32-128 | 32 | 32/80| 64(+128)/128 | 32 | 8-32/80| 64(+128)/128 | 32 | 64 | 36 | 8-128 | 51 |
| Pentium 4 D/EE (Athlon 64*) | 64/80| 64/64 | 64 | 8-64/80|64 + 128/32-128 | 64 | 64/80|64 + 128/128 | 64 | 8-64/80|64 + 128/128 | 64 | 64(+16) | 40 | 8-128 | 52 |
| Atom | 32-64/80| 64/64-128 | 64 | 8-64/80|64 + 128/32-128 | 64 | 64/80|64 + 128/128 | 64 | 8-64/80|64 + 128/128 | 64 | 64 | 36 | 8-128 | 51 |
| Core 2 (i7*) | 64/80| 128/128 | 64 | 8-64/80|64 + 128/32-128 | 64 | 64/80|64 + 128/128 | 64 | 8-64/80|64 + 128/128 | 64 | 64 (192+16) | 40 | 8-128 | 52 |
| Athlon II*, Phenom (II)* | 64/80| 128/128 | 64 | 8-64/80|64 + 128/32-128 | 64 | 64/80|64 + 128/128 | 64 | 8-64/80|64 + 128/128 | 64 | 128+16 | 40 (48) | 8-128 | 52 |
* — Мультиплексированная шина данных и адреса (для ЦП с интегрированным контроллёром памяти — только межпроцессорная)
«A/B|C/D» — для данных указана разрядность скалярного целого / вещественного | векторного целого / вещественного доменов
«X+Y» — имеет домены этого вида двух разрядностей
«X-Y» — в зависимости от команды или ФУ принимает все промежуточные значения с целой степенью двойки
Если вы дочитали до этого места, то объявленная цель статьи, скорее всего, уже достигнута, а Идеальное Конечное Точное Определение разрядности так и не найдено. Может быть, его вообще нет, и это даже хорошо. В конце концов, если компьютер это главный инструмент для работы с информацией, то каждая IT-технология это метод улучшения работы компьютера. Разрядность сама по себе ничего не даст в отрыве от всего остального арсенала высоких инфотехнологий. PDA/коммуникаторы, мобильники, нетбуки, медиа-плееры и прочая карманная электроника, а также гигантское количество встроенных контроллёров и бортовых компьютеров отлично работают, увеличивая свою популярность и без всякой 64-битности. Так зачем тогда переходят на большие разрядности? Зачем, например, никому пока не нужная 64-битность в Intel Atom для нетбуков, где 8 ГБ памяти мало того, что никому не нужны, так ещё и за пару часов досуха выжмут батарею, а научные или экономические вычисления (где могут потребоваться 64 целых бита) никто запускать не будет? Один из возможных ответов: «потому что мы можем». Дополнительная пара миллионов транзисторов для удвоения ещё оставшихся 32-битными блоков утонет каплей в море вентилей, уже потраченных на всё остальное в этом же чипе. Галопирующий прогресс микроэлектроники как главного паровоза IT сделал интегральный транзистор таким дешёвым, что теперь лакомый для любого маркетолога шильдик «64 bit» обойдётся потребителю в десяток лишних центов, обеспечивая совсем не бутафорское, а вполне реальное ускорение на 10-50 % в 1-5 % приложений. И если мелкая овчинка стоит почти бесплатной выделки, почему нет?