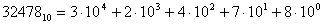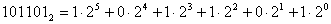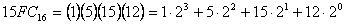Что такое развернутая форма записи числа информатика
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
§ 1.1. Системы счисления
Информатика. 8 класса. Босова Л.Л. Оглавление
Ключевые слова:
1.1.1. Общие сведения о системах счисления
Система счисления — это знаковая система, в которой приняты определённые правила записи чисел. Знаки, с помощью которых записываются числа (рис. 1.1), называются цифрами, а их совокупность — алфавитом системы счисления.
В любой системе счисления цифры служат для обозначения чисел, называемых узловыми; остальные числа (алгоритмические) получаются в результате каких-либо операций из узловых чисел.
Пример 1. У вавилонян узловыми являлись числа 1, 10, 60; в римской системе счисления узловые числа — это 1, 5, 10, 50, 100, 500 и 1000, обозначаемые соответственно I, V, X, L, С, D, М.
Рис. 1.1. Знаки, используемые для записи чисел в различных системах счисления
Системы счисления различаются выбором узловых чисел и способами образования алгоритмических чисел. Можно выделить следующие виды систем счисления:
Простейшая и самая древняя система — так называемая унарная система счисления. В ней для записи любых чисел используется всего один символ — палочка, узелок, зарубка, камушек. Длина записи числа при таком кодировании прямо связана с его величиной, что роднит этот способ с геометрическим представлением чисел в виде отрезков. Именно унарная система лежит в фундаменте арифметики, и именно она до сих пор вводит первоклассников в мир счёта. Унарную систему ещё называют системой бирок.
Система счисления называется непозиционной, если количественный эквивалент (количественное значение) цифры в числе не зависит от её положения в записи числа.
Пример 2. В древнеегипетской системе счисления числа 1, 2, 3, 4, 10, 13, 40 обозначались соответственно следующим образом:
Те же числа в римской системе счисления обозначаются так: I, II, III, IV, X, XIII, XL. Здесь алгоритмические числа получаются путём сложения и вычитания узловых чисел с учётом следующего правила: каждый меньший знак, поставленный справа от большего, прибавляется к его значению, а каждый меньший знак, поставленный слева от большего, вычитается из него.
Система счисления называется позиционной, если количественный эквивалент цифры зависит от её положения (позиции) в записи числа.Основание позиционной системы счисления равно количеству цифр, составляющих её алфавит.
Десятичная система
Десятичная система записи чисел, которой мы привыкли пользоваться в повседневной жизни, с которой мы знакомы с детства, в которой производим все наши вычисления, — пример позиционной системы счисления. Алфавит десятичной системы составляют цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Алгоритмические числа образуются в ней следующим образом: значения цифр умножаются на «веса» соответствующих разрядов, и все полученные значения складываются. Это отчётливо прослеживается в числительных русского языка, например: «три-ста пять-десят семь».
Основанием позиционной системы счисления может служить любое натуральное число q > 1. Алфавитом произвольной позиционной системы счисления с основанием q служат числа 0, 1, …, q—1, каждое из которых может быть записано с помощью одного уникального символа; младшей цифрой всегда является 0.
Основные достоинства любой позиционной системы счисления — простота выполнения арифметических операций и ограниченное количество символов, необходимых для записи любых чисел.
В позиционной системе счисления с основанием q любое число может быть представлено в виде:
Запись числа по формуле (1) называется развёрнутой формой записиСвёрнутной формой записи числа называется его представление в виде 1 ± an-1an-2…a1a0,a-1…a-m. 1 Далее будут рассматриваться только положительные целые числа.
Пример 3. Рассмотрим десятичное число 14351,1. Его свёрнутая форма записи настолько привычна, что мы не замечаем, как в уме переходим к развёрнутой записи, умножая цифры числа на «веса» разрядов и складывая полученные произведения:
1.1.2. Двоичная система счисления
Двоичной системой счисления называется позиционная система счисления с основанием 2. Для записи чисел в двоичной системе счисления используются только две цифры: 0 и 1.
На основании формулы (1) для целых двоичных чисел можно записать:
Такая форма записи «подсказывает» правило перевода натуральных двоичных чисел в десятичную систему счисления: необходимо вычислить сумму степеней двойки, соответствующих единицам в свёрнутой форме записи двоичного числа.
Получим правило перевода целых десятичных чисел в двоичную систему счисления из формулы (1′).
Разделим аn-1 • 2 n-1 + аn-2 • 2 n-2 + … + а0 • 2 0 на 2. Частное будет равно аn-1 • 2 n-2 + … + а1, а остаток будет равен а0.
Полученное частное опять разделим на 2, остаток от деления будет равен а1.
Если продолжить этот процесс деления, то на n-м шаге получим набор цифр:
которые входят в двоичное представление исходного числа и совпадают с остатками при его последовательном делении на 2.
Таким образом, для перевода целого десятичного числа в двоичную систему счисления нужно последовательно выполнять деление данного числа и получаемых целых частных на 2 до тех пор, пока не получим частное, равное нулю. Исходное число в двоичной системе счисления составляется последовательной записью полученных остатков, начиная с последнего.
Пример 4. Переведём десятичное число 11 в двоичную систему счисления. Рассмотренную выше последовательность действий (алгоритм перевода) можно изобразить так:
Выписывая остатки от деления в направлении, указанном стрелкой, получим: 1110 = 10112.
Пример 5. Если десятичное число достаточно большое, то более удобен следующий способ записи рассмотренного выше алгоритма:
1.1.3. Восьмеричная система счисления
Восьмеричной системой счисления называется позиционная система счисления с основанием 8. Для записи чисел в восьмеричной системе счисления используются цифры: 0, 1,2, 3, 4, 5, 6, 7.
На основании формулы (1) для целого восьмеричного числа можно записать:
Например: 10638 = 1 • 8 3 + 0 • 8 2 + 6 • 8 1 + 3 • 8 0 = 56310.
Таким образом, для перевода целого восьмеричного числа в десятичную систему счисления следует перейти к его развёрнутой записи и вычислить значение получившегося выражения.
Для перевода целого десятичного числа в восьмеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 8 до тех пор, пока не получим частное, равное нулю. Исходное число в новой системе счисления составляется последовательной записью полученных остатков, начиная с последнего.
Пример 6. Переведём десятичное число 103 в восьмеричную систему счисления.
1.1.4. Шестнадцатеричная система счисления
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, Е, F.
Здесь только десять цифр из шестнадцати имеют общепринятое обозначение 0,…, 9. Для записи цифр с десятичными количественными эквивалентами 10, 11, 12, 13, 14, 15 обычно используются первые пять букв латинского алфавита.
Таким образом, запись 3AF16 означает:
Пример 7. Переведём десятичное число 154 в шестнадцатеричную систему счисления.
1.1.5. Правило перевода целых десятичных чисел в систему счисления с основанием q
Для перевода целого десятичного числа в систему счисления с основанием q следует:
Представим таблицу соответствия десятичных, двоичных, восьмеричных и шестнадцатеричных чисел от 0 до 2010.
В Единой коллекции цифровых образовательных ресурсов (http://sc.edu.ru/) размещена интерактивная анимация «Преобразование десятичного числа в другую систему счисления» (135050). С её помощью можно понаблюдать за переводом произвольного целого числа от 0 до 512 в позиционную систему счисления, основание которой не превышает 16.
В размещённой там же виртуальной лаборатории «Цифровые весы» (135009) вы сможете освоить ещё один способ перевода целых десятичных чисел в другие системы счисления — метод разностей.
1.1.6. Двоичная арифметика
Арифметика двоичной системы счисления основывается на использовании следующих таблиц сложения и умножения:
Пример 8. Таблица двоичного сложения предельно проста. Так как 1 + 1 = 10, то 0 остаётся в младшем разряде, а 1 переносится в старший разряд.
Пример 9. Операция умножения двоичных чисел выполняется по обычной схеме, применяемой в десятичной системе счисления, с последовательным умножением множимого на очередную цифру множителя.
Таким образом, в двоичной системе счисления умножение сводится к сдвигам множимого и сложениям.
1.1.7. «Компьютерные» системы счисления
В компьютерной технике используется двоичная система счисления, обеспечивающая ряд преимуществ по сравнению с другими системами счисления:
Обмен информацией между компьютерными устройствами осуществляется путём передачи двоичных кодов. Пользоваться такими кодами из-за их большой длины и зрительной однородности человеку неудобно. Поэтому специалисты (программисты, инженеры) на некоторых этапах разработки, создания, настройки вычислительных систем заменяют двоичные коды на эквивалентные им величины в восьмеричной или шестнадцатеричной системах счисления. В результате длина исходного слова сокращается в три, четыре раза соответственно. Это делает информацию более удобной для рассмотрения и анализа.
С помощью ресурса «Интерактивный задачник, раздел “Системы счисления»» (128659), размещённого в Единой коллекции цифровых образовательных ресурсов, можно проверить, насколько прочно вы усвоили изученный в этом параграфе материал.
Самое главное о системе счисления
Система счисления — это знаковая система, в которой приняты определённые правила записи чисел. Знаки, с помощью которых записываются числа, называются цифрами, а их совокупность — алфавитом системы счисления.
Система счисления называется позиционной, если количественный эквивалент цифры зависит от её положения (позиции) в записи числа. Основание позиционной системы счисления равно количеству цифр, составляющих её алфавит.
Основанием позиционной системы счисления может служить любое натуральное число q > 1.
В позиционной системе счисления с основанием q любое число может быть представлено в виде:
Вопросы и задания
1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Что вы можете сказать о формах представления информации в презентации и в учебнике? Какими слайдами вы могли бы дополнить презентацию?
10. Верны ли следующие равенства? а) 334 = 217;
б) 338 = 214.
11. Найдите основание х системы счисления, если: а) 14х = 910;
б) 2002х = 13010.
19. Вычислите выражения: а) (11111012 + AF16) : 368; б) 1258 + 1012 ∙ 2A16 − 1418. Ответ дайте в десятичной системе счисления.
Как записать число в развернутой форме информатика
2.5. РАЗВЕРНУТАЯ ФОРМА ЧИСЛА
Развернутая форма записи числа – это запись в виде разрядных слагаемых, записанных с помощью степени соответствующего разряда и основания степени (основание счета).
1. Десятичная система:
Пронумеруем разряды, начиная с младшего:
Теперь запишем выражение:
2. Двоичная система:
Пронумеруем разряды, начиная с младшего:
3. Шестнадцатеричная система:
Пронумеруем разряды, начиная с младшего:
Другие системы счисления записываются аналогично вышеприведенным системам с тем лишь исключением, что основание степени будет соответствовать основанию счета.
В позиционной системе счисления число можно представить в развернутой форме (в виде суммы разрядных слагаемых) и в свернутой форме. Именно такой формой записи чисел мы и пользуемся в повседневной жизни. Иначе свернутую форму записи называют естественной или цифровой.
Десятичное число А10= 4718,63 в развернутой форме будет имеет вид:
Рассмотрим еще примеры записи чисел в развернутом виде
58910 → 500 + 80 + 9 = 5*100 + 8*10 + 9*1 = 5*10 2 +8*10 1 + 9*10 0

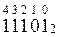

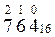
Задания для самостоятельной работы
Задание 1. Запишите числа в развернутой форме
| 1) | 11110102 | 6) | 111101,0012 | 11) | 1110,112 | 16) | 100011102 |
| 2) | 2174,55 | 7) | 5771,0015 | 12) | 89784515 | 17) | 514763175 |
| 3) | 6479118 | 8) | 1622,848 | 13) | 1114878 | 18) | 113874,3348 |
| 4) | 1214710 | 9) | 512001410 | 14) | 1874,59610 | 19) | 1554,01410 |
| 5) | 1247,032116 | 10) | 15789416 | 15) | 163201,9816 | 20) | 88541216 |
Перевод чисел в десятичную систему счисления
1. Записать число в развернутом виде
2. Выполнить вычисления как в десятичной системе счисления
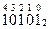
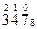
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Студент – человек, постоянно откладывающий неизбежность. 10571 – 

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, программирование, полезный материал и многое другое.
Как от свёрнутой формы записи десятичного числа перейти к его развёрнутой форме?
Ответ
Рассмотрим десятичное число 14351,1. Его свёрнутая форма записи настолько привычна, что мы не замечаем, как в уме переходим к развёрнутой записи, умножая цифры числа на «веса» разрядов и складывая полученные произведения:
Переход от свернутой формы к развернутой
1. Посмотрите на данное вам число и определите количество его цифр.
Пример:
Напишите 5827 в развернутом виде.
Прочитайте число вслух: пять тысяч восемьсот двадцать семь.
Обратите внимание, что в этом числе есть четыре цифры. В результате развернутая форма будет содержать четыре слагаемых.
2. Перепишите число в виде суммы его цифр, оставив между ними некоторое расстояние, чтобы умножить каждую цифру на некоторую цифру (об этом далее).
Пример:
5827 перепишите так:
3. Цифры числа расположены в определенных позициях, которые соответствуют (справа налево) единицам, десяткам, сотням, тысячам и так далее. Определите название позиции и ее значение для каждой цифры (справа налево).
Пример:
Так как в данном числе четыре цифры, то вам нужно определить названия четырех позиций (справа налево).
7 соответствует единицам (значение = 1 = 10 0 ).
2 соответствует десяткам (значение = 10 = 10 1 ).
8 соответствует сотням (значение = 100 = 10 2 ).
5 соответствует тысячам (значение = 1000 = 10 3 ).
4. Умножьте каждую цифру данного числа на значение соответствующей ей позиции.
Пример:
5 · 10 3 + 8 · 10 2 + 2 · 10 1 + 7 · 10 0
Конспект к уроку информатики: «Системы счисления. Понятия, виды, развернутая форма записи числа»
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Подробный конспект урока.
Системы счислений. Понятие, виды, развернутая форма записи числа и ее применение.
Автор/ы урока (ФИО, должность)
Тип урока (мероприятия, занятия)
Получение новых знаний
Цели урока (мероприятия, занятия)
(образовательные, развивающие, воспитательные)
Актализировать полученные ранее знания о системах счисления, оганизовать деятельность обучающихся по овладению способностью применять рузвернутую форму записи числа и умением применять её для перевода чисел в позиционной системе счислений из недесятичного числа в десятичное
Задачи урока (мероприятия, занятия)
сформулировать понятийный аппарат по данной теме;
раскрыть принципиальные отличия позиционной системы счисления от непозиционной системы счисления;
организовать деятельность по формированию умений применять развернутую форму записи числа для перевода числа из недесятичной системы счислений, в десятичную.
Используемые педагогические технологии, методы и приемы
ИКТ- технологии, диффиренцированные задания, проблемый метод, работа в парах, технологии личностно-ориентированного обучения, деятельностный подход
Время реализации урока (мероприятия, занятия)
По программе в учебное время 1 академический час
Знания, умения, навыки и качества, которые актуализируют/приобретут/
Учащиеся актуализируют ранее полученные знания о системах счислений, приобретают знания
закрепят/др. ученики в ходе урока (мероприятия, занятия)
об основаниях систем счисления, разрядности систем счисления, умения переводить числа из недесятичной системы счислений, в десятичную. Формируют навык применения развернутой формы записи числа.
Необходимое оборудование и материалы
Компьютер, мультимедиапректор, экран.
Дидактическое обеспечение урока (мероприятия, занятия)
Презентация, дидактический материал для домашнего задания
Список учебной и дополнительной литературы
Учебник по информатике Н.Д. Угринович Информатика 8 класс
Ход и содержание урока (мероприятия, занятия),
деятельность учителя и учеников.
Подробное описание всех этапов урока (мероприятия, занятия).
1. Организационный этап
Приветствие учащихся; фиксация отсутствующих; проверка подготовленности учащихся к уроку (рабочее место, рабочая поза, внешний вид); организация внимания
2. Этап проверки домашнего задания
3.Актуализация знаний и мотивация
На слайде размещены этапы урока
Проанализируйте, подумайте в какой последовательности эти этапы нужно расставить и сформулируйте цели сегодняшнего урока
Определяют тему урока
Понятие система счислений, вспомните с 5 класса что это такое. Приведите примеры
Формулируют определение, приводят примеры (римская, арабская)
4. Этап усвоения новых знаний
На слайде две формулировки определений системы счисления и виды системы счисления прочитайте, определите, к какой системе какое определение относится
Анализируют определения, соотносят определения с понятиями
На слайде Изображены числа Римской с счисления и с арабской к какому виду систем счисления они относятся
Показываю 2-ую систему счисления, алфавит, основание, предлагаю по примеру записать предложенные с. сч.
Записывают в тетради.
Сформулируйте, что такое основание системы счисления
Показываю РФЗЧ, объясняю обозначения,
Записывают РФЗЧ, обозначения
Что обзначает запись на слайде?
Определяют, что из любой с сч. С помощью РФЗЧ можно перевести в десятичную
6. Этап проверки усвоения учащимися нового материала
Предлагаю обратится к РФЗЧ и перевести 101001 2 в десяичную, на слайде поэтапно появляютя элементы перевода
Переводят, находят результат
7. Этап закрепления нового материала
Даю обучающимся дифференцировнную практическую работу
Выплняют по уровням
Предлагаю поменятся тетрадями, проверить правильность выполнения
Меняются тетрадями, провряют друг у друга
Ключи на листочках
Задание из ЕГЭ (сначала выходит задание с вариантами, затем можно использовать подсказку (клик на ключике), затем кликом выбрать для проверки предлагаемый вариант) Щелкнув по звезде, на слайде появляется решение.
Рефлексия деятельности на уроке (мероприятии, занятии)
Предлагаю вернуться к этапам урока, поговариваем цели каждого, были ли достигнуты цели? Что нового почерпали с данной темой. Слайд 9
Домашнее задание (если это необходимо на уроке)
Раздаю листки с д.з.,
Дополнительная необходимая информация
Данная тема рассматривает задачи, которые есть в заданиях по ЕГЭ
Ссылки на использованн
Обоснование, почему данную тему оптимально изучать с использованием медиа-, мультимедиа, каким образом осуществить
Более наглядно представлена информация о системах счислений. Лучше восприятие детьми, экономия рабочего времени.
Советы по логическому переходу от данного урока к последующим
После этого урока целесообразно дать урок по теме «Перевод из двоичной системы счислений в восмеричную, шестнадцатиричную и обратно»