Что такое регуляризация в машинном обучении
Регуляризация
| Определение: |
| Регуляризация (англ. regularization) в статистике, машинном обучении, теории обратных задач — метод добавления некоторых дополнительных ограничений к условию с целью решить некорректно поставленную задачу или предотвратить переобучение. Чаще всего эта информация имеет вид штрафа за сложность модели. |
Содержание
Мотивация [ править ]
Как говорилось ранее, регуляризация полезна для борьбы с переобучением. Если вы выбрали сложную модель, и при этом у вас недостаточно данных, то легко можно получить итоговую модель, которая хорошо описывает обучающую выборку, но не обобщается на тестовую.
На примере линейной регрессии [ править ]
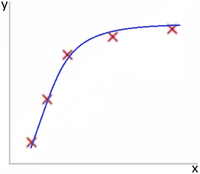
На Рис. 1 представлена зависимость, которая хорошо подходит для описания данных, а на Рис. 2 — модель, слишком сильно заточенная под обучающую выборку.
Однин из способов бороться с негативным эффектом излишнего подстраивания под данные — использование регуляризации, т. е. добавление некоторого штрафа за большие значения коэффициентов у линейной модели. Тем самым запрещаются слишком «резкие» изгибы, и предотвращается переобучение.
На примере логистической регрессии [ править ]
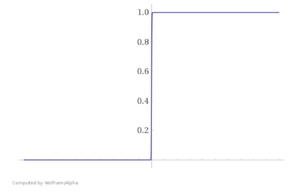
Необходимость регуляризации можно увидеть и на другом примере — при использовании логистической регресии. Представьте, что ваша обучающая выборка была линейно разделима. В таком случае в процессе оптимизации значения весов модели уйдут в бесконечность, и вместо сигмойды получится «ступенька», представленная на Рис. 3.
Это плохо, ибо произошло затачивание под обучающую выборку. Как и в предыдущем примере, побороться с этим можно путем добавления регуляризатора, не дающего весам принимать слишком большие значения.
Основные виды регуляризации [ править ]
В представленных ниже формулах для эмпирического риска [math]Q[/math] : [math]\mathcal
Запишем задачу настройки вектора параметров [math]\beta[/math] :
где [math]\mathcal
[math]\begin
В новых переменных функционал становится гладким, но добавляются ограничения-неравенства:
Эластичная сеть [ править ]
Вероятностная интерпретация регуляризации [ править ]
Эквивалентная вероятностная задача [ править ]
Перед нами стоит задача — минимизировать эмпирический риск:
[math]Q(\beta, X^l)=\sum\limits _
[math]p(X^l|\beta)=\prod\limits_
Удобнее рассматривать логарифм правдоподобия:
[math]L(\beta, X^l)=\ln p(X^l|\beta)=\sum\limits_
Можно заключить, что задачи в исходном и вероятностном представлении эквивалентны, если положить:
[math]-\ln p(x_, y_|\beta)=\mathcal
Принцип максимума совместного правдоподобия данных и модели [ править ]
[math]p(X^l, \beta; \gamma)=p(X^l|\beta)p(\beta;\gamma)[/math]
Таким образом, приходим к принципу максимума совместного правдоподобия данных и модели:
[math]L_<\gamma>(\beta, X^l)=\ln p(X^l, \beta;\gamma)=\sum\limits_
Функционал [math]L_<\gamma>[/math] распадается на два слагаемых: логарифм правдоподобия и регуляризатор, не зависящий от данных. Второе слагаемое ограничивает вектор параметров модели, не позволяя ему быть каким угодно.
В итоге мы получили, что с байесовской точки зрения многие методы регуляризации соответствуют добавлению некоторых априорных распределений на параметры модели. При этом можно определить распределения, которые соответствуют представленным ранее [math]L_<1>[/math] и [math]L_<2>[/math] регуляризаторам.
Нормальный регуляризатор [ править ]
[math]\beta \sim N(0, \sigma^2)[/math]
Логарифмируя, получаем квадратичный регуляризатор:
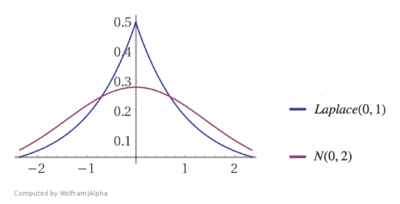
Лапласовский регуляризатор [ править ]
[math]\beta \sim Laplace(0, C)[/math]
Регуляризация в линейной регрессии [ править ]
$g(x, \beta) = \sum\limits_
В итоге оптимизируемый функционал эмпирического риска выглядит следующим образом:
Гребневая регрессия [ править ]
Итоговый минимизируемый функционал с поправкой:
Оценим эффект, который оказывает добавление гребня. Выразим регуляризованное МНК-решение через сингулярное разложение:
Теперь найдём регуляризованную МНК-аппроксимацию целевого вектора y:
Поэтому данный метод называют также сжатие или сокращение весов.
В нерегуляризованном случае:
В случае с гребнем:
Лассо регрессия [ править ]
Итоговый минимизируемый функционал с поправкой:
Сравнение гребневой и лассо регрессий [ править ]
В случае с гребневой регрессией:
В случае с лассо регрессией:
$\beta_
Регуляризация в алгоритмах [ править ]
Градиентный спуск [ править ]
[math]Q(w, X^l)=\sum\limits_
где [math]\eta \gt 0[/math] — величина шага в направлении антиградиента.
Регуляризация — одна из эвристик улучшения градиентных методов обучения. Основным способом уменьшить переобучение является квадратичная регуляризация, называемая также сокращением весов. Чтобы ограничить рост абсолютных значений весов, к минимизируемому функционалу [math]Q(w)[/math] добавляется штрафное слагаемое:
Это приводит к появлению аддитивной поправки в градиенте:
[math]Q_<\tau>‘(w) = Q′(w) + \tau w[/math]
В результате правило обновления весов принимает вид:
Регуляризация предовтращает паралич, повышает устойчивость весов в случае мультиколлинеарности, повышает обобщающую способность алгоритма и снижает риск переобучения. Однако есть и недостатки — параметр [math]\tau[/math] необходимо выбирать с помощью кросс-валидации, что связано с большими вычислительными затратами.
Метод опорных векторов [ править ]
Метод опорных векторов (SVM) используется для задач классификации и регрессии. В нем строится гиперплоскость, разделяющая объекты выборки оптимальным образом.
Другие использования регуляризации [ править ]
Логистическая регрессия [ править ]
Как было показано в мотивационном примере, для логистической регрессии может быть полезно использовать регуляризацию.
Аналогично можно использовать и другие регуляризаторы.
Нейронные сети [ править ]
Для нейронной сети помимо добавления штрафного слагаемого к эмпирическому риску активно используют и другой метод борьбы с переобучением — прореживание сети (англ. dropout), в ходе которого упрощают сеть, руководствуясь правилом — если функция ошибки не изменяется, то сеть можно упрощать и дальше. Подробнее об этом можно почитать в статье, рассказывающей о практике реализации нейронных сетей.
Регуляризация
| Определение: |
| Регуляризация (англ. regularization) в статистике, машинном обучении, теории обратных задач — метод добавления некоторых дополнительных ограничений к условию с целью решить некорректно поставленную задачу или предотвратить переобучение. Чаще всего эта информация имеет вид штрафа за сложность модели. |
Содержание
Мотивация [ править ]
Как говорилось ранее, регуляризация полезна для борьбы с переобучением. Если вы выбрали сложную модель, и при этом у вас недостаточно данных, то легко можно получить итоговую модель, которая хорошо описывает обучающую выборку, но не обобщается на тестовую.
На примере линейной регрессии [ править ]
На Рис. 1 представлена зависимость, которая хорошо подходит для описания данных, а на Рис. 2 — модель, слишком сильно заточенная под обучающую выборку.
Однин из способов бороться с негативным эффектом излишнего подстраивания под данные — использование регуляризации, т. е. добавление некоторого штрафа за большие значения коэффициентов у линейной модели. Тем самым запрещаются слишком «резкие» изгибы, и предотвращается переобучение.
На примере логистической регрессии [ править ]
Необходимость регуляризации можно увидеть и на другом примере — при использовании логистической регресии. Представьте, что ваша обучающая выборка была линейно разделима. В таком случае в процессе оптимизации значения весов модели уйдут в бесконечность, и вместо сигмойды получится «ступенька», представленная на Рис. 3.
Это плохо, ибо произошло затачивание под обучающую выборку. Как и в предыдущем примере, побороться с этим можно путем добавления регуляризатора, не дающего весам принимать слишком большие значения.
Основные виды регуляризации [ править ]
В представленных ниже формулах для эмпирического риска [math]Q[/math] : [math]\mathcal
Запишем задачу настройки вектора параметров [math]\beta[/math] :
где [math]\mathcal
[math]\begin
В новых переменных функционал становится гладким, но добавляются ограничения-неравенства:
Эластичная сеть [ править ]
Вероятностная интерпретация регуляризации [ править ]
Эквивалентная вероятностная задача [ править ]
Перед нами стоит задача — минимизировать эмпирический риск:
[math]Q(\beta, X^l)=\sum\limits _
[math]p(X^l|\beta)=\prod\limits_
Удобнее рассматривать логарифм правдоподобия:
[math]L(\beta, X^l)=\ln p(X^l|\beta)=\sum\limits_
Можно заключить, что задачи в исходном и вероятностном представлении эквивалентны, если положить:
[math]-\ln p(x_, y_|\beta)=\mathcal
Принцип максимума совместного правдоподобия данных и модели [ править ]
[math]p(X^l, \beta; \gamma)=p(X^l|\beta)p(\beta;\gamma)[/math]
Таким образом, приходим к принципу максимума совместного правдоподобия данных и модели:
[math]L_<\gamma>(\beta, X^l)=\ln p(X^l, \beta;\gamma)=\sum\limits_
Функционал [math]L_<\gamma>[/math] распадается на два слагаемых: логарифм правдоподобия и регуляризатор, не зависящий от данных. Второе слагаемое ограничивает вектор параметров модели, не позволяя ему быть каким угодно.
В итоге мы получили, что с байесовской точки зрения многие методы регуляризации соответствуют добавлению некоторых априорных распределений на параметры модели. При этом можно определить распределения, которые соответствуют представленным ранее [math]L_<1>[/math] и [math]L_<2>[/math] регуляризаторам.
Нормальный регуляризатор [ править ]
[math]\beta \sim N(0, \sigma^2)[/math]
Логарифмируя, получаем квадратичный регуляризатор:
Лапласовский регуляризатор [ править ]
[math]\beta \sim Laplace(0, C)[/math]
Регуляризация в линейной регрессии [ править ]
$g(x, \beta) = \sum\limits_
В итоге оптимизируемый функционал эмпирического риска выглядит следующим образом:
Гребневая регрессия [ править ]
Итоговый минимизируемый функционал с поправкой:
Оценим эффект, который оказывает добавление гребня. Выразим регуляризованное МНК-решение через сингулярное разложение:
Теперь найдём регуляризованную МНК-аппроксимацию целевого вектора y:
Поэтому данный метод называют также сжатие или сокращение весов.
В нерегуляризованном случае:
В случае с гребнем:
Лассо регрессия [ править ]
Итоговый минимизируемый функционал с поправкой:
Сравнение гребневой и лассо регрессий [ править ]
В случае с гребневой регрессией:
В случае с лассо регрессией:
$\beta_
Регуляризация в алгоритмах [ править ]
Градиентный спуск [ править ]
[math]Q(w, X^l)=\sum\limits_
где [math]\eta \gt 0[/math] — величина шага в направлении антиградиента.
Регуляризация — одна из эвристик улучшения градиентных методов обучения. Основным способом уменьшить переобучение является квадратичная регуляризация, называемая также сокращением весов. Чтобы ограничить рост абсолютных значений весов, к минимизируемому функционалу [math]Q(w)[/math] добавляется штрафное слагаемое:
Это приводит к появлению аддитивной поправки в градиенте:
[math]Q_<\tau>‘(w) = Q′(w) + \tau w[/math]
В результате правило обновления весов принимает вид:
Регуляризация предовтращает паралич, повышает устойчивость весов в случае мультиколлинеарности, повышает обобщающую способность алгоритма и снижает риск переобучения. Однако есть и недостатки — параметр [math]\tau[/math] необходимо выбирать с помощью кросс-валидации, что связано с большими вычислительными затратами.
Метод опорных векторов [ править ]
Метод опорных векторов (SVM) используется для задач классификации и регрессии. В нем строится гиперплоскость, разделяющая объекты выборки оптимальным образом.
Другие использования регуляризации [ править ]
Логистическая регрессия [ править ]
Как было показано в мотивационном примере, для логистической регрессии может быть полезно использовать регуляризацию.
Аналогично можно использовать и другие регуляризаторы.
Нейронные сети [ править ]
Для нейронной сети помимо добавления штрафного слагаемого к эмпирическому риску активно используют и другой метод борьбы с переобучением — прореживание сети (англ. dropout), в ходе которого упрощают сеть, руководствуясь правилом — если функция ошибки не изменяется, то сеть можно упрощать и дальше. Подробнее об этом можно почитать в статье, рассказывающей о практике реализации нейронных сетей.
L1 и L2 регуляризация
Feb 13, 2020 · 5 min read
Меня зовут Леонид, и я врач, который пытается разобраться в базовых принципах машинного обучения. И это мой первый пост, наверно вообще в жизни.
Дисклеймер: я не претендую на академичность или точные определения в своем посте. Все что тут написано лично мой опыт который (так же как и все остальное в интернете) не надо брать за истину. Nullius in verba.
Я уже пол года прохожу различные обучающие онлайн курсы, ни одного не завершил по обстоятельствам основной работы. Поэтому хотел создать небольшой блог с памятками, чтобы материал который я пытался вспомнить оставался тут.
“Коротко об основных остановках на дороге машинного обучения.”
Один из с а мых закрытых вопросов касается регуляризации. Все основные формулы, не похожи друг на друга и поэтому можно узнать как устроен тот или иной этап (от входного нейрона до обратного распространения ошибки), просто посмотрев различные источники которые объяснят на примерах или под другим углом. Но вот регуляризация остается всегда регуляризацией, почувствовать ее для меня было очень трудно. То есть я понимал что для некоторых задач она значима, но не мог представить как она работает.
Сперва нужно определить, что перееобучение — это когда какие то веса (w) имеют слишком большой показатель (нейроны с большими весами “стягивают” на себя все признаки, сужая “просвет”, что не позволяет сети работать в полевых условиях).
По рисунку мы можем сказать, что некоторая нейросеть которая имеет очень много признаков (весов) которые имеют пики и хорошо подходят для тестовых данных, не сможет работать на новых данных.
Получается чем более линейная функция, тем более она недообучена. И чтобы сделать функцию “более линейной” прибавляются суммы весов к ошибке.
Чтобы понять регуляризацию, начал с того, что часик побаловался в песочнице tensorflow. Стало понятно что L1 регуляризация стабильно выключает ненужные нейроны зануляя весы. Получается тренировка максимально быстро и точно.
В итоге, регуляризация:
Короче, это про упрощение и сглаживание.
В ML есть два основных вида регуляризации. Википедия их описывает так:
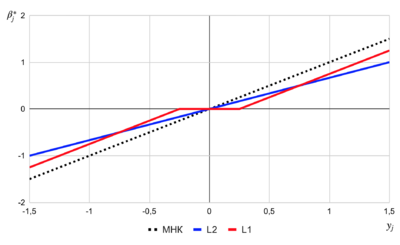
L1-регуляризация (англ. lasso regression), или регуляризация через манхэттенское расстояние:
Если короче, то прибавление к лосс-функции суммы весов в модуле. Она добавляет « критическую величину» коэффициента, как дополнение к функции потерь. То есть, если весы на расстоянии лямбда ближе к нулю, то они становятся равными нулю и уходят в игнор, тем самым отбирая только важные признаки и в следствии уменьшая саму сеть, что экономит ресурсы.
В графике расстояние лямбда прижимается к нулю. Это расстояние и выключает низкие веса.
Меня на самом деле беспокоит до сих пор вопрос про переобучение. Понятно, что система с большим количеством признаков и пиками на этих признаках обращает внимание только на них. Реуляризация же наоборот избавляется от ненужных признаков (шумов) и упрощает саму модель. Но не будет ли такая модель упрощена до степени переобучения на определенной цели. То есть для чего то одного простого такая сеть подойдет, но стоит внести какие то дополнения (это легко понять если представить более сложное изображение с дополнительными признаками, допустим цветовой эмоции) то достигнуть цели станет просто невозможно. Поэтому наверно нужно быть предельно осторожным с регуляризацией и не быть довольными только тестовыми данными.
L2- регуляризация, или регуляризация Тихонова (в англоязычной литературе — ridge regression или Tikhonov regularization), для интегральных уравнений позволяет балансировать между соответствием данным и маленькой нормой решения:
Тут получается что функция занижает пики прибавляя сумму весов в квадрате с множителем лямбда.
В графике происходит легкое смещение (не дисперсия) добавляя статистическую ошибку, которая не влияет на точность, но позволяет не переобучиться. Соответственно если вы поставите большую коэффициент (лямбда) L2, то система никогда не обучится, просто из-за того что сильно сместиться. Но если лямбда будет маленькой то и смещение будет маленьким, и весь смысл регуляризации так же будет минимальным.
Член λ называется параметром сглаживания. Он балансирует кросс-энтропийную функцию ошибок и регуляризационный штраф. Если значение λ велико, весовые коэффициенты будут стремиться к нулю, если же значение λ мало или равно нулю, то весовые коэффициенты будут просто стремиться к минимизации кросс-энтропийной функции ошибок. Как правило, значение параметра λ устанавливают 0,1 или 1, или в районе между этими значениями, но в основном его значение зависит от конкретных данных. Вам нужно попробовать разные значения и понаблюдать за поведением функции затрат и конечным результатом. Не существует универсальной методики определения значения параметра λ. (craftappmobile.com )
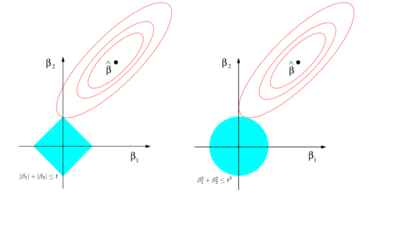
В сумме можно посмотреть на этот рисунок
Регуляризация создает некое абстрактное поле (зеленое) в градиентном спуске (слоистые овалы) из которого не может выйти обучение сети. Когда на самом деле абсолютное дно обучения (B с шапочкой) находится за пределами этого поля. При этом логически если мы увеличиваем Лямбду, то поле сужается, то есть с увеличением шкалы нормализации весов, найти какое либо дно станет труднее (возникнет “пересглаженность” 🙂 ).
По идее регуляризация выдрана из контекста сглаживающих методов среди которых есть еще и генетические методы, LARS и даже полный перебор.
Спасибо за внимание! Если интересно, то буду писать дальше…
Алгоритмы машинного обучения простым языком. Часть 2
Jun 7, 2019 · 4 min read
Ридж- и лассо- регрессия
Моя бабушка до сих пор не очень напугана, поэтому продолжаем!
Линейная регрессия не такая уж и пугающая, правда? Это просто метод нахождения связи между чем-то.
Теперь, когда мы знаем, что такое линейная регрессия, можем поговорить о других методах, похожих на неё, например, о ридж-регрессии.
Для понимания линейной регрессии надо было понять метод градиентного спуска. Точно так же для понимания ридж-регрессии необходимо понять, что такое регуляризация.
Специалисты машинного обучения используют методы регуляризации для того, чтобы удостовериться, что модель принимает решение на основании независимых переменных, которые оказывают значительное влияние на результирующую переменную.
Наверн о е ты думаешь, какая вообще разница, на какие переменные ориентируется наша модель? Ведь если переменные не имеют никакого влияния, то модель линейной регрессии должна их просто проигнорировать. На самом деле всё не так. Мы рассмотрим детали чуть позже, но если говорить вкратце, то мы создаём модель и даём ей кучу данных для обучения. Затем мы тестируем её на тестовых данных. Таким образом, если модель будет учитывать все независимые переменные, то она будет выдавать очень хороший результат на тренировочных данных, но очень плохой на тестовых. Это происходит, потому что модель получается не гибкой и показывает не очень хорошую производительность на данных, которые не содержат каждую, даже малейшую толику того, на чём мы её обучали. Это называется переобучением.
Чтобы понять, что такое переобучение, рассмотрим пример (довольно длинный):
Представим, что недавно ты стала мамой и твой ребёнок очень любит макароны. При этом каждый раз, когда ребёнок ест макароны, окно на кухне приоткрыто, ведь ты любишь прохладу. Затем твой племянник дарит ребёнку комбинезон, и ты начинаешь кормить его макаронами только тогда, когда он одет в этот комбинезон. Вдруг ты решаешь завести собаку, и эта собака исправно сидит рядом с ребёнком в то время, пока он кушает макароны, чтобы ловить то, что упало на пол. Что происходит: ты кормишь ребёнка макаронами, окно на кухне открыто, ребёнок одет в его специальный комбинезон, рядом сидит собака. Так как это твой первый ребёнок, ты думаешь, что он ест макароны только из-за этих трёх окружающих вещей: открытое окно, собака и комбинезон. На этот момент времени твоя модель кормления ребёнка макаронами довольно сложна.
Однажды ты решаешь сходить в гости к бабушке. Тебе нужно покормить ребёнка ужином (конечно же, макаронами). Ты начинаешь паниковать, ведь на кухне нет окна, ты забыла комбинезон дома, и за собакой сейчас присматривают соседи. Тебя настолько выбивает из колеи, что ты вообще забываешь покормить ребёнка и укладываешь его спать голодным.
Вау. Твои действия были неправильными, потому что ты встретилась со сценарием, который не встречала ранее. Однако дома тебе всегда удавалось кормить ребёнка.
После пересмотра модели кормления ребёнка и избавления от “шумов” (вещей, которые, по-твоему, не влияли на любовь ребёнка к макаронам), ты осознаешь единственное, что имеет значение — ты готовишь макароны.
Следующим вечером ты кормишь ребёнка его любимыми макаронами на кухне у бабушки, совсем без окон, в одних только подгузниках и без собаки. И всё проходит хорошо! Теперь твоё понимание того, почему он ест макароны, гораздо проще.
Это то, что делает регуляризация для модели машинного обучения. Она помогает модели обращать внимание лишь на те признаки, которые действительно имеют значение, и избавляться от шумов.
Во всех типах регуляризации присутствует штраф, обозначаемый греческой буквой лямбда: λ. Именно он позволяет сократить количество шумов в данных.
В ридж-регрессии, также называемой L2-регрессией, штраф — это сумма квадратов коэффициентов переменных. Коэффициенты линейной регрессии — просто числа, которые прикреплены к каждой независимой переменной и определяют влияние этой переменной на результирующую переменную. Иногда их называют весами. В ридж-регрессии штрафы уменьшают коэффициенты при соответствующих независимых переменных, но никогда не обнуляют их. Это значит, что шумы всегда будут влиять на результат, но в очень маленькой степени.
Второй тип регуляризации — лассо или L1-регуляризация. Вместо того, чтобы начислять штрафы за каждый признак в данных, штрафы в ней начисляются лишь за признаки с большим значением коэффициентов. К тому же лассо может обнулять значения коэффициентов, тем самым полностью убирая признак из датасета (так как при вычислении результирующей переменной соответствующий признак будет умножен на ноль). Таким образом, с регрессией лассо модель может полностью избавиться от шумов в данных. В некоторых случаях это бывает очень и очень полезно!