Что такое ргр в начертательной геометрии
Начертательная геометрия (1 семестр)
Инженерная графика.
Расчетно-графические работы (РГР)
Методические указания для самостоятельной работы студентов направления: 140400 – Электроэнергетика и электротехника (профиль «Электроснабжение»)
Методические указания включают: шесть расчетно-графических работ (1 семестр) и шесть расчетно-графических работ (2 семестр).
Каждая РГР включает: задание, исходные данные по вариантам, указания по решению и оформлению, пример выполнения, вопросы для самопроверки, рекомендуемую литературу.
Методические указания предназначены в качестве пособия для самостоятельной работы при выполнении расчетно-графических работ по «Инженерной графике» для студентов направления: 140400 – Электроэнергетика и электротехника (профиль «Электроснабжение»).
к.т.н., доцент кафедры ТОММ СТИ НИТУ МИСиС А.В.Александров.
к.т.н., доцент кафедры техники и технологии горного производства Губкинского института (филиала) МГОУ А.А. Паршин.
Под редакцией Г.И.Фурсовой
Губкинский институт (филиал) Московского государственного открытого университета, 2011
Содержание
Семестр
Вопросы для самопроверки 19
2 семестр20
Вопросы для самопроверки 69
Введение.
Дисциплина «Инженерная графика» состоит из двух структурно и методически согласованных разделов: «Начертательная геометрия», изучаемая в 1 семестре, и «Инженерная графика», изучаемая во 2 семестре.
Образец


Министерство образования и науки Российской Федерации
Московский государственный открытый университет
Губкинский институт (филиал)
Кафедра теоретической и прикладной механики
ИНЖЕНЕРНАЯ ГРАФИКА
Расчетно-графические работы
Выполнил: Студент_____________
Группа ___________
Шифр ______________
Проверил: ____________________
Губкин
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
РГР №1Построить линию пересечения треугольников АВС и EDK и показать видимость их в проекциях.
Определить натуральную величину треугольника АВС. Данные для своего варианта взять из табл.1. Пример выполнения приведен на рис.1.
| № варианта | Размеры и координаты, мм | ||||||||||||||||
| XА | YA | ZA | XB | YB | ZB | XC | YC | ZC | XD | YD | ZD | XE | YE | ZE | XK | YK | ZK |
Указания к решению РГР 1. В левой половине листа формата А3 (297х420м) намечаются оси координат и из табл.1 согласно своему варианту берутся координаты точек А, В, С, D, E, K вершин треугольника (рис.1). Стороны треугольников и другие вспомогательные прямые проводятся вначале тонкими сплошными линиями. Линии пересечения треугольников строятся по точкам пересечения сторон одного треугольника с другим или по точкам пересечения каждой из сторон одного треугольника с другим порознь. Такую линию можно построить, используя и вспомогательные секущие проецирующие плоскости.
Видимость сторон треугольника определяется способом конкурирующих точек. Видимые отрезки сторон треугольников выделяют сплошными толстыми линиями, невидимые следует показать штриховыми линиями. Определяется натуральная величина треугольника АВС.
Плоскопараллельным перемещением треугольник АВС приводится в положение проецирующей плоскости и далее вращением вокруг проецирующей прямой в положение, когда он будет параллелен плоскости проекций.
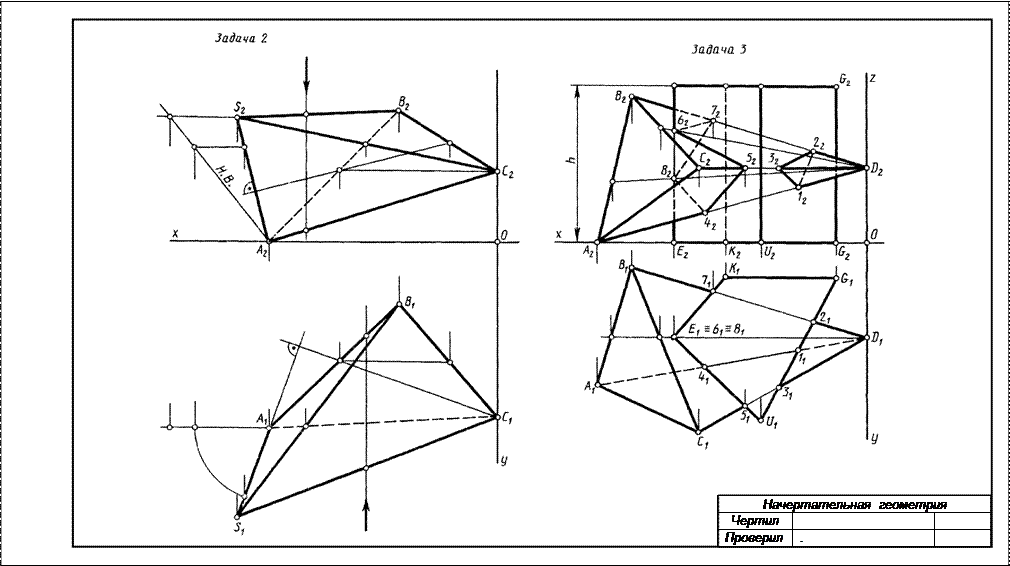
РГР №2 Построить проекции пирамиды, основанием которой является треугольник АВС, а ребро SА определяет высоту h пирамиды. Данные для своего варианта взять из табл.2. Пример выполнения см. на рис.2.
| № варианта | Координаты и размеры, мм | ||||||||
| XА | YA | ZA | XB | YB | ZB | XC | YC | ZC | h |
Указания к решению РГР 2. В левой половине листа формата А3 намечаются оси координат и из табл.2 согласно своему варианту берутся координаты точек А, В и С вершин треугольника АВС. По координатам строится треугольник в проекциях. В точке А восставляется перпендикуляр к плоскости треугольника и на нем выше этой плоскости откладывается отрезок АS, равный заданной величине h. Строятся ребра пирамиды. Способом конкурирующих точек определяется их видимость. Видимые ребра пирамиды следует показать сплошными толстыми линиями, невидимые – штриховыми линиями. Все вспомогательные построения необходимо сохранить на эпюре и показать их тонкими сплошными линиями.
РГР №3Построить линию пересечения пирамиды с прямой призмой. Данные для своего варианта взять из табл.3. Пример выполнения см. на рис.2.
| № варианта | Координаты и размеры, мм | |||||||||||||||||||||||
| XА | YA | ZA | XB | YB | ZB | XC | YC | ZC | XD | YD | ZD | XE | YE | ZE | XK | YK | ZK | XG | YG | ZG | XU | YU | ZU | h |
Указания к решению РГР 3. В оставшейся правой половине листа формата А3 намечаются оси координат и из табл.3 согласно своему варианту берутся координаты точек А, В, С и D вершин пирамиды и координаты точек Е, К, G и U вершин многоугольника нижнего основания призмы, а также высота h призмы. По этим данным строятся проекции многогранников (пирамида и призма). Призма своим основанием стоит на плоскости уровня, горизонтальные проекции ее вертикальных ребер преобразуются в точки. Грани боковой поверхности призмы представляют собой отсеки горизонтально проецирующих плоскостей.
Линии пересечения многогранников определяются по точкам пересечения ребер каждого из них с гранями другого многогранника или построением линии пересечения граней многогранника. Соединяя каждые пары таких точек одних и тех же граней отрезками прямых, получаем линию пересечения многогранников.
Видимыми являются только те стороны многоугольника пересечения, которые принадлежат видимым граням многогранников. Их следует показать сплошными толстыми линиями, невидимые отрезки пространственной ломаной показать штриховыми линиями.
Задаче уделить особое внимание. Все построения на чертеже тщательно проверить. Допущенные ошибки приводят к неправильному решению следующей РГР – РГР № 4 (построение развертки многогранников).
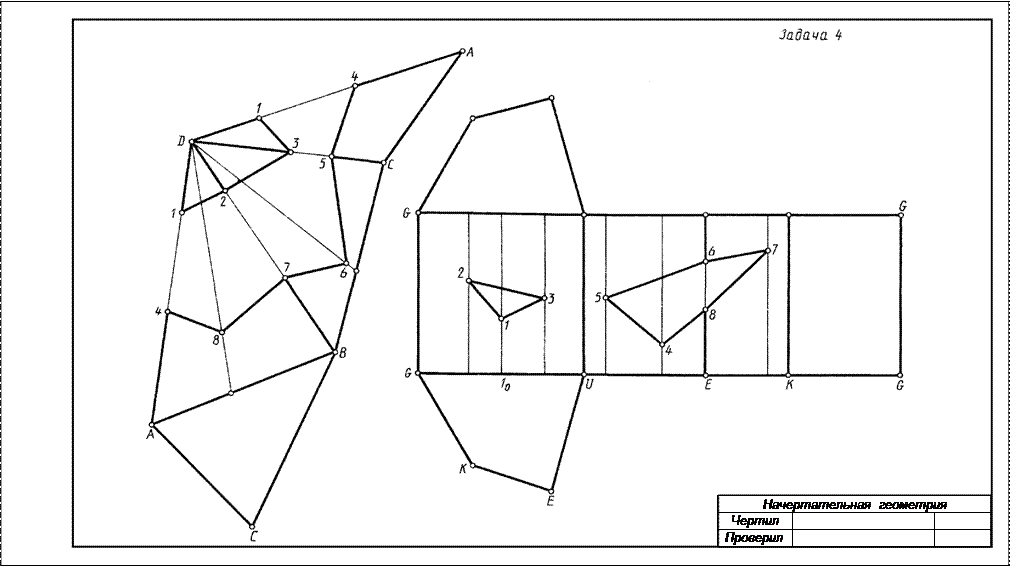
РГР №4Построить развертки пересекающихся многогранников – прямой призмы с пирамидой. Показать на развертках линию их пересечения. Пример выполнения приведен на рис.3.
Указания к решению РГР 4. Чтобы решить данную задачу, следует перевести на кальку формата 297х420мм чертеж пересекающихся многогранников с задачи 3. Здесь же выполнить вспомогательные построения для определения натуральных величин ребер многогранников.
На листе бумаги ватман формата А3 (297х420мм) строятся развертки многогранников.
Развертка прямой призмы. Для построения развертки прямой призмы поступают следующим образом:
а) проводят горизонтальную прямую;
б) от произвольной точки G этой прямой откладывают отрезки GU, UE, EK, KG, равные длинам сторон основания призмы;
в) из точек G, U, … восставляют перпендикуляры и на них откладывают величины, равные высоте призмы. Полученные точки соединяют прямой. Прямоугольник GG1G1G является разверткой боковой поверхности призмы. Для указания на развертке граней призмы из точек U, E, K восставляют перпендикуляры;
г) для получения полной развертки поверхности призмы к развертке поверхности пристраивают многоугольники ее оснований.
Для построения на развертке линии пересечения призмы с пирамидой замкнутых ломаных линий 1 2 3 и 4 5 6 7 8 пользуемся вертикальными прямыми. Например, для определения положения точки 1 на развертке поступаем так: на отрезке GU от точки G вправо откладываем отрезок G10, равный отрезку G1 (рис.3).
Из точки 10 восставляем перпендикуляр к отрезку GU и на нем откладываем аппликату z точки 1. Аналогично строят и находят остальные точки.
Развертка пирамиды. На кальке определяют натуральную величину каждого из ребер пирамиды. Зная натуральные величины ребер пирамиды, строят ее развертку. Определяют последовательно натуральные величины граней пирамиды. На ребрах и на гранях пирамиды (на развертке) определяют вершины пространственной ломанной пересечения пирамиды с призмой.


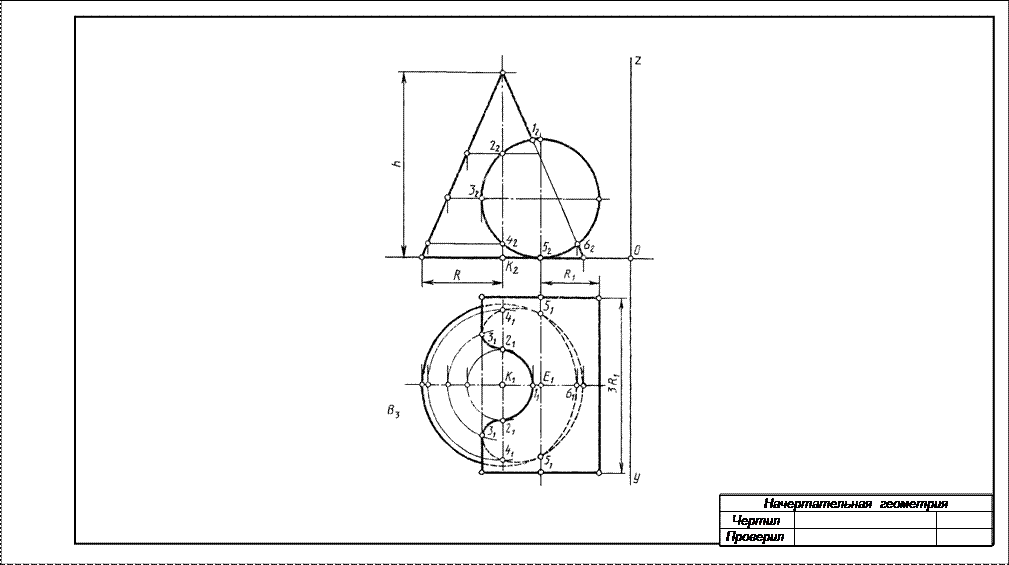
РГР №5На трехпроекционном чертеже построить недостающие проекции сквозного отверстия в сфере заданного радиуса R. Вырожденная (фронтальная) проекция сквозного отверстия представлена четырехугольником: координаты проекций точек А, В, С и D вершин четырехугольника – сквозного отверстия на сфере – известны (табл.4). Пример выполнения приведен на рис.4
| № варианта | Координаты и размеры, мм | ||||||||||||||
| XО | YО | ZО | XА | YA | ZA | XB | YB | ZB | XC | YC | ZC | XD | YD | ZD | R |
| — | — | — | — | ||||||||||||
| — | — | — | — | ||||||||||||
| — | — | — | — | ||||||||||||
| — | — | — | — | ||||||||||||
| — | — | — | — | ||||||||||||
| — | — | — | — | ||||||||||||
| — | — | — | — | ||||||||||||
| — | — | — | — | ||||||||||||
| — | — | — | — | ||||||||||||
| — | — | — | — | ||||||||||||
| — | — | — | — | ||||||||||||
| — | — | — | — | ||||||||||||
| — | — | — | — | ||||||||||||
| — | — | — | — | ||||||||||||
| — | — | — | — | ||||||||||||
| — | — | — | — | ||||||||||||
| — | — | — | — | ||||||||||||
| — | — | — | — |
Указание к решению РГР № 5. Намечаются оси координат с началом координат в центре листа формата А3. Строятся проекции сферы заданного радиуса R с центром в точке О. Определяются по заданным координатам (табл.4) проекции точек А, В, С и D (вершин четырехугольника) сквозного отверстия на сфере и строится многоугольник – вырожденная проекция линии сквозного отверстия. Далее задача сводится к определению недостающих проекций точек поверхности сферы.
Вначале определяются характерные точки линии сквозного отверстия: точки на экваторе, главном меридиане, наиболее удаленные и ближайшие точки поверхности сферы к плоскостям проекций.
РГР №6Построить линию пересечения конуса вращения с цилиндром вращения. Оси поверхностей вращения – взаимно перпендикулярные проецирующие скрещивающиеся прямые. Данные для своего варианта взять из табл.5 Пример выполнения приведен на рис.5
| № варианта | Координаты и размеры, мм | |||||||
| XК | YК | ZК | R | h | XЕ | YЕ | ZЕ | R1 |
Указания к решению РГР №6.В правой половине листа намечают оси координат и из табл.4 берут согласно своему варианту величины, которыми задаются поверхности конуса вращения и цилиндра вращения. Определяют центр (точка К) окружности радиуса R основания конуса вращения в горизонтальной координатной плоскости. На вертикальной оси на расстоянии h от плоскости уровня и выше ее определяют вершину конуса вращения.
Осью цилиндра вращения является фронтально-проецирующая прямая точки Е; основаниями цилиндра являются окружности радиуса R1. Образующие цилиндра имеют длину, равную 3R1, и делятся пополам фронтальной меридиональной плоскостью конуса вращения.
С помощью вспомогательных секущих плоскостей определяют точки пересечения очерковых образующих одной поверхности с другой и промежуточные точки линии пересечения поверхностей. Проводя вспомогательную секущую фронтальную меридиональную плоскость конуса вращения, определяют точки пересечения главного меридиана (очерковых образующих) конуса вращения с параллелью (окружностью) проецирующего цилиндра. Выбирая горизонтальную секущую плоскость, проходящую через ось цилиндра вращения, определяют две точки пересечения очерковых образующих цилиндра с поверхностью конуса.
Высшую и низшую, а также промежуточные точки линии пересечения поверхности находят с помощью вспомогательных горизонтальных плоскостей – плоскостей уровня. По точкам строят линию пересечения поверхности конуса вращения с цилиндром вращения и устанавливают ее видимость в проекциях.

Вопросы для самопроверки
1.Проекционный метод отображения пространства на плоскость.
2. Виды проецирования.
3.Основные свойства центрального проецирования.
4.Основные свойства ортогонального проецирования.
5.Координатный метод. Комплексный чертеж Монжа.
6.Задание точки, прямой, плоскостей и многогранников на комплексном чертеже Монжа.
7.Проекции прямых общего и частных положений.
8.Точка на прямой. Следы прямой.
9.Прямые уровня. Задание прямых уровня на комплексном чертеже.
10.Проецирующие прямые. Задание проецирующих прямых на комплексном чертеже.
11.Взаимное положение двух прямых в пространстве.
12.Различные способы задания плоскости на чертеже.
13.Следы плоскости. Треугольник следов, основные свойства.
14.Положение плоскости относительно плоскостей проекций.
15.Плоскости уровня. Основные свойства.
16.Проецирующие плоскости. Основные свойства.
17.Главные линии плоскости.
18.Точка в плоскости.
19.Взаимное положение плоскостей в пространстве.
20.Взаимное положение прямой и плоскости в пространстве.
21.Линия ската плоскости.
22.Теорема о проекции прямого угла.
23.Геометрические преобразования. Метод перемены плоскостей проекций.
26.Метод плоскопараллельного перемещения.
27.Многогранники. Пересечение многогранников плоскостью и прямой.
29.Кривые линии. Плоские и пространственные кривые линии.
30.Касательные и нормали к кривым линиям. Особые точки кривых.
31.Кривые второго порядка.
32.Поверхности, классификация, определитель.
33.Кинематический и каркасный способы задания поверхностей. Критерии заданности поверхности.
34.Поверхности вращения, классификация.
35.Сечение поверхности вращения проецирующей плоскостью и плоскостью общего положения.
36.Построение линии пересечения двух поверхностей вращения.
37.Линейчатые поверхности. Классификация.
38.Поверхности с тремя направляющими. Поверхности с плоскостью параллелизма. Конические и цилиндрические поверхности общего вида.
39.Винтовые поверхности. Классификация. Линейчатые винтовые поверхности. Циклические поверхности.
40.Способы построения линии пересечения поверхностей (метод вспомогательных секущих плоскостей, метод концентрических и эксцентрических сфер). Алгоритмы решения задач.
41.Касательные линии и плоскости к поверхности. Построение нормали к поверхности.
42.Построение разверток поверхностей (точные, условные).
43.Аксонометрические проекции. Стандартные виды аксонометрических проекций.
44.Окружность общего и частного положения в аксонометрической проекции.
Изучение курса инженерной графики (2 семестр) должно основываться на теоретических положениях курса начертательной геометрии, нормативных документах и государственных стандартах ЕСКД.
Основные вопросы инженерной графики рассматриваются на практических занятиях и закрепляются работой с рабочими тетрадями по инженерной графике и выполнением расчетно-графических работ. Кроме того, значительную часть необходимой информации студенты должны приобретать в процессе самостоятельной работы изучением учебной и справочной литературы.
При изучении инженерной графики предусмотрено выполнение шести расчетно-графических работ. К зачету допускают студентов, выполнивших и защитивших все работы. а протяжении всего курса предусматривается постоянное развитие навыков по выполнению и чтению чертежей и схем. Все чертежи выполняются в карандаше.
Выполнение расчетно-графических работ рекомендуется вести в следующем порядке:
1. Ознакомиться с темой по программе и методическими указаниями к выполнению РГР.
2. Изучить стандарты, необходимые для выполнения РГР по данной теме.
3. Изучить рекомендуемую литературу по данной теме. Желательно законспектировать в рабочей тетради основные положения и зарисовать отдельные чертежи.
4. Ответить на вопросы для самопроверки к каждой теме программы и записать ответы в рабочей тетради.
5. Выполнить РГР в порядке, указанном в методических указаниях к РГР.
Чертежи, помещенные в методических указаниях, не являются эталонами исполнения, а служат лишь примерами расположения материала на листе, характеризуют объем и содержание темы.




| МГОУ 04.01.10 | |||
| Геометрическое черчение | Литера | Масса | Масштаб |
| У | 1:1 | ||
| Разраб. | Ф.И.О. | ||
| Проверил | |||
| Лист | Листов | ||
| Группа Шифр | |||
| Н.контр. | |||
| Утв. |
РГР № 1. Требования, предъявляемые стандартами ЕСКД к выполнению чертежей. Построение очертания кулачка
Задание по РГР №1 Построить очертание кулачка. Пример выполнения дан на рис.2, данные для своего варианта взять из табл.1.
Графическую работу выполняют на листе чертежной бумаги формата А3 карандашом.
Порядок выполнения. Изучить основные положения ГОСТ 2.301-68, 2.302-68, 2.303-68, 2.304-81, 2.306-68, 2.307-68, данные в сборнике стандартов «Единая система конструкторской документации», и рекомендуемую литературу. Ознакомиться с содержанием чертежа к РГР 1 (рис.2). Прочитать «Основные рекомендации по выполнению чертежей» данных методических указаний. Указания по выполнению РГР 1. В связи с огромным развитием автоматики можно встретить в самых разнообразных механизмах плоские кулачки и копиры. В заданиях к теме 1 очертания кулачков включают две лекальные кривые и дугу радиуса R, угол которой определяет время «выстоя» механизма, получающего движение от кулачка.
Построение очертания кулачка в каждом варианте следует начинать с нанесения осей координат Ох и Оу. Затем строят лекальные кривые по их заданным параметрам и выделяют участки, входящие в очертание кулачка. После этого можно вычертить главные переходы между лекальными кривыми. При этом следует учесть, что во всех вариантах через точку D проходит касательная к эллипсу.
В табл.1 обозначение Rх показывает, что величина радиуса определяется построением. На чертеже вместо Rх надо проставить соответствующее число со знаком «Ú».

Таблица 1. Данные для построения очертания кулачка (размеры, мм)
РГР по начертательной геометрии
 Ответы на вопросы по заказу заданий по начертательной геометрии:
Ответы на вопросы по заказу заданий по начертательной геометрии:







Содержание:
Примеры решения экзаменационных РГР по начертательной геометрии
Построить точку пересечения прямой а с плоскостью α, определить видимость.
а) Заключаем прямую a в плоскость β; α∩β=12
б) Находим проекцию точки 1 на плоскости π1
в) Проводим прямую а2 до пересечения с осью х, получаем т. 22
г) Находим проекцию т. 2 в плоскости π1
е) Определяем видимость.
Возможно, вас также заинтересует эта ссылка:
Определить истинную величину отрезка АВ.
а) Проводим горизонталь h2 через т. А2
б) Полученное расстояние от т. В2 до р откладываем на перпендикуляре от т. В1 в плоскости π1
в) А1 В01 – истинная величина
Возможно, вас также заинтересует эта ссылка:
Найти величину перпендикуляра, опущенного из точки М на плоскость АВС.
а) Проводим в π2 горизонталь h2 II оси х, замечаем точку 12, находим ее проекцию 11 в π1, проводим h1
б) Проводим в π1фронталь f1 II оси х, замечаем точку 21, находим ее проекцию 22 в π2, проводим f2
в) Опускаем перпендикуляр из т. M2 на f2
г) Опускаем перпендикуляр из т. M1 на h1
д) Заключаем перпендикуляр из т. М2 в плоскость α2
е) Плоскость α2 ∩ (ABC) = 32 42, находим их проекции в плоскости π1
з) Находим длину МК, для этого в π2 замечаем длину перпендикуляра
М2 К2 = L (измерения производить перпендикулярно оси х)
и) В π1 перпендикулярно М1 К1 из т. М1 выводим перпендикуляр и откладываем длину L, получаем т. М01; длина К1 М01 – истинная величина перпендикуляра М К.
Возможно, вас также заинтересует эта ссылка:
Построить третью (профильную) проекцию пирамиды. Найти точку N на горизонтальной, профильной проекциях и в аксонометрической проекции пирамиды.
а)Строим профильную проекцию пирамиды:
— проецируем точки основания пирамиды и вершину на ось Z;
— с π1проецируем точки на ось Y, а затем под углом 45 0 на профильную плоскость π3;
— засекаем высоту вершины пирамиды относительно ее проекции в π2, получаем проекцию пирамиды на π3
б) Через существующую проекцию т. N и вершину пирамиды S проводим прямую до пересечения с ребром основания АВ, получаем т. 12 и находим ее проекции в плоскостях π1 и π3, соединяем с вершиной S
в) Перпендикулярно оси х проецируем т. Т на плоскость π1 и затем на π3
г) Строим аксонометрическую проекцию пирамиды, оси х, y выполняются под углом 120 0 относительно оси z, величины принимаются 1:1
д) Находим проекцию т. N в аксонометрии:
— соединяем т. 1 с проекцией вершины Sи находим проекцию т.N на данной прямой; поднимаем вертикальную ось из данной точки;
— далее соединяем т. 1 с вершиной S и на пересечении данной прямой 1S и вертикальной оси из горизонтальной проекции т. N будет определено месторасположеие т. N
Возможно, вас также заинтересует эта ссылка:
Определить расстояние между параллельными прямыми.
а) Производим замену плоскости π1 на π4 II прямым а1 и b1
б) Находим проекции прямых а4 и b4 согласно высотам в плоскости π2
в) Производим замену плоскости π4 на π5 перпендикулярно прямым а4 и b4; перпендикулярно оси х45 переносятся проекции прямых, проецирующихся в точку (расстояния от оси х45 откладываются согласно расстоянию от прямых до оси х14)
Возможно, вас также заинтересует эта ссылка:
Построить точку пересечения прямой L с плоскостью ABC, определить видимость
а) Заключаем прямую L в плоскость α2
б) Она засекает т. 1 и 2 в π2, находим проекции точек в плоскости π1
г) Находим проекцию К2 в π2
д) Определяем видимость
Возможно, вас также заинтересует эта ссылка:
Определить какой из отрезков длиннее
а) т.к. прямая АС II оси х12 – она является фронталью и уже имеет натуральную величину,
б) Определяем натуральную величину АВ:
— проводим в π2 через т. А горизонталь h2 II оси х;
— опускаем из т. B2 перпендикуляр на горизонталь;
в) Откладываем в π1 на перпендикуляре от АВ из т. В длину перпендикуляра, получаем т. В01; отрезок А1 В01 – истинная аеличина
г) Сравниваем длины отрезков Н.В. : АС >АВ
Возможно, вас также заинтересует эта ссылка:
Способом замены плоскостей проекций определить истинную величину треугольника АВС
а) Проводим из т. С2 горизонталь h2 II оси х, на АВ замечаем т. 12, проецируем ее в π1, находим т. 11 на А1 В1
б) Перпендикулярно h1 в проекции С производим замену плоскости проекций π4
в) Проецируем точки АВС на π4 перпендикулярно оси х14 и отмечаем проекции точек согласно высотам в плоскости π2 соответственных точек
г) II А4 В4 С4 вводим плоскость π5 и проецируем перпендикулярно оси х45; точки А5 В5 С5, откладываем на расстоянии от точек А1 В1 С1 до х14
д) А5 В5 С5 – натуральная величина плоскости АВС
Построить сечение пирамиды плоскостью, заданной двумя пересекающимися прямыми. Найти его натуральную величину
а) В плоскости π1 перпендикулярно h1 производим замену плоскости проекций π4; сносим проекции точек пирамиды и плоскости (h∩f)
в) Строим натуральную величину сечения 2345, для этого производим замену плоскости проекции π4 на π5 II (h4 ∩f4 ), и перпендикулярно оси х45 проецируем точки сечения в новую плоскость
г) Для определения месторасположения точек рассмотрим π1, находим длины отрезков от точек сечения до оси х14 и отмечаем соответствующие длины на соответствующих проекциях точек сечения
д) Соединяем полученные точки получаем сечение 2345 – натуральная величина
Определить точки пересечения прямой L с конусом
а) Прямую L2 заключаем в плоскость α2, α2 пересекает поверхность конуса, проецируем точки пересечения на горизонтальную ось конуса в проекции π1, и проводим данным радиусом окружность
б) Проведенная окружность пересекает проекцию прямой L1 в точках 11 21, находим проекции точек в π2 – 12 22
в) Определяем видимость.
Построить сечение конуса и цилиндра, определить видимость
а) Рассмотрим проекции тел вращения в π2:
— образующая конуса S2 K2 пересекает цилиндр в т. 12 и 22, проецируем точки на горизонтальную ось конуса, проходящую через вершину S, в плоскости π1;
б) В плоскости π2 проводим секущие плоскости α1, α2, α3, α4, данные плоскости пересекают и конус и цилиндр, находим общие точки пересечения, проецируем их в π1на соответствующие сечения плоскостями
в) Соединяем точки сечения
г) Определяем видимость
Построить точку пересечения прямой а с плоскостью α, определить видимость
а) Заключаем прямую a в плоскость β; α∩β=12
б) Находим проекцию точки 1 на плоскости π1
в) Проводим прямую а2 до пересечения с осью х, получаем т. 22
г) Находим проекцию т. 2 в плоскости π1
е) Определяем видимость.
Достроить горизонтальную проекцию многоугольника АВСDE и найти его натуральную величину
а) Соединяем A2 D 2 ; из точки Е2 проводим прямую через т. С2; A2 D 2 ∩ Е2 С2=12; находим проекцию т. 11 и проводим через нее и т. Е1 прямую; прямая Е111 пересекается с проекционной линией т. С, получаем ее горизонтальную проекцию С1
б) Определяем месторасположение т. В1:
— в проекции π2 через т.В2 и 12 проводим прямую, пересекающую сторону Е2 D 2 в точке 22, находим ее проекцию в π1т. 21;
— в проекции π1проводим прямую 11 21 до пересечения с проекционной линией т. В, получаем ее горизонтальную проекцию В1;
г)Определяем натуральную величину А ЕDCB:
— в π2 через т. Е2 проводим горизонталь h2; h2 ∩ В2 С2=32; находим ее горизонтальную проекцию на В1 С1, определяем положение h1;
— перпендикулярно h1 вводим новую проекцию π4 и проецируем на нее, перпендикулярно оси х14, плоскость АЕDCB (она занимает проецирующее положение);
— II А4 Е4 D4 C4 B4 вводим новую плоскость π5 и проецируем на нее точки плоскости, с учетом длин в проекции π1, т.е. удаление от точек проекции π1 до оси х14
Найти величину перпендикуляра, опущенного из точки М на плоскость АВС
а) Проводим в π2 горизонталь h2 II оси х, замечаем точку 12, находим ее проекцию 11 в π1, проводим h1
б) Проводим в π1фронталь f1 II оси х, замечаем точку 21, находим ее проекцию 22 в π2, проводим f2
в) Опускаем перпендикуляр из т. M2 на f2
г) Опускаем перпендикуляр из т. M1 на h1
д) Заключаем перпендикуляр из т. М2 в плоскость α2
е) Плоскость α2 ∩ (ABC) = 32 42, находим их проекции в плоскости π1
з) Находим длину МК, для этого в π2 замечаем длину перпендикуляра
М1 К1 = L (измерения производить перпендикулярно оси х)
и) В π1 перпендикулярно М1 К1 из т. М1 выводим перпендикуляр и откладываем длину L, получаем т. М01; длина К1 М01 – истинная величина перпендикуляра М К.
16. Построить линию пересечения призмы и конуса.
а) Рассмотрим π1: находим середины сторон призмы: 11, 21, 31 и их проекции во фронтальной плоскости
б) Продливаем прямые S1 31; S1 21;S1 11 до пересечения с основанием конуса в т. 6 1,51,41 соответственно
г) Определяем точки пересечения данных прямых с проекциями середин отрезков призмы
д) Определяем линию пересечения призмы и конуса
Построить линию пересечения двух плоскостей, определить видимость линий
Построить точку пересечения прямой L с плоскостью ABC, определить видимость
б) Через вершину А2 и проекцию прямой L2 (точка) проводим прямую и засекаем ее в плоскость α2; α2∩( ABC)= 12; находим ее проекцию в π1и соединяем с вершиной А1
в) 11 А1 ∩ L1=М1— точка пересечения прямой и плоскости
Построить вторую проекцию прямой, принадлежащей плоскости α
а) Проецируем точки прямой на плоскость α π2 и определяем проекции на ось х12
б) II α π1 из проекций на оси х12 проводим лучи, засекающие проекционные лучи точек прямой АВ в точках А 1В1
Построить линию пересечения плоскости i со сферой
а) Плоскость i засекает сферу в π2 в т. 12 22; проецируем точки на горизонтальную ось проекции π1, получаем т. 11 21
а) Согласно заданным координатам откладываем проекции точек в соответствии с установленными направлениями осей;
б) Каждая точка должна иметь три проекции.
Построить призму SABC в аксонометрической проекции
г) Строим аксонометрическую проекцию пирамиды, оси х, y выполняются под углом 120 0 относительно оси z, величины принимаются 1:1
Построить сечение способом концентрических сфер
а) Находим центр пересечения осей конусов 02
б) Опускаем из 02 перпендикуляр на образующую прямого конуса, получаем т. S2, проводим луч II основанию прямого конуса.
в) Окружность радиусом R1 пересекает образующую наклонного конуса в т. 12; II основанию наклонного конуса проводим луч из т. 12, который пересекает луч из т. S2 в точке 22
г)Рассмотрим видимые пересечения конусов в точках 32 и 42
д) Соединяем получившиеся точки 22, 32, 42 – линия пересечения двух конусов.
Построить точку пересечения прямой L с плоскостью ABC, определить видимость
б) Через вершину А1 и проекцию прямой L1 (точка) проводим прямую и засекаем ее в плоскость α1; α1∩( ABC)= 11; находим ее проекцию в π2и соединяем с вершиной А2
в) 12 А2 ∩ L2=М1— точка пересечения прямой и плоскости
Построить вторую проекцию треугольника АВС, принадлежащего плоскости α
а) Рассмотрим π2,проецируем точки плоскоасти АВС на проекцию απ2 II оси х12 получаем точки А`2, В`2, С`2 и проецируем их на ось х12
б) II плоскости απ1 из проекций А`1, В`1, С`1 проводим лучи, которые засекутся с проекциями точек А2, В2, С2 в проекциях точек А1, В1, С1
Построить линию пересечения плоскости i с конусом
а) Плоскость i сечет конус в точках 1222, проецируем их в π1 на горизонтальную ось конуса
б) i2 пересекает вертикальную ось конуса в т. 32 перпендикулярно вертикальной оси конуса проводим секущую плоскость; получившимся радиусом R1 в π1проводим окружность и проецируем на данную окружность проекции точек 31 3`1
в) Определяем сечение и видимость.
а) Согласно заданным координатам откладываем проекции точек в соответствии с установленными направлениями осей;
б) Каждая точка должна иметь три проекции.
Определить расстояние между параллельными прямыми а и b
Определить точку пересечения L с плоскостью, заданной прямыми АВ и АС
б) Через вершину А2 и проекцию прямой L2 (точка) проводим прямую и засекаем ее в плоскость α2; α2∩( ABC)= 12; находим ее проекцию в π1и соединяем с вершиной А1
в) 11 А1 ∩ L1=М1— точка пересечения прямой и плоскости
Построить вторую проекцию плоского четырехугольника, если даны три точки, принадлежащие его плоскости
а) Соединяем точки АВС; в π2 проводим диагонали у четырехугольника К2 М2 Р 2Т2
б) Диагонали пересекают плоскость АВС в точках 62 52 42 32
в) Сторона четырехугольника МР∩( ABC)= 12 и 22
г) Находим проекции 11 21 31 41 51 61 в плоскости π1 на соответствующих сторонах плоскости
д)Определяем диагонали и находим на них с помощью проекционных лучей из плоскости π2 проекции точек К1 М1 Р 1Т1
Вращением вокруг оси i совместить точку К с плоскостью α
б) В π1 II плоскости απ1из т. 11 проводим луч
в) i – ось вращения, вращаем т. К1,до совмещения ее с лучом из т. 11, получаем т. К’1
г) Находим на пересечении проекционных лучей т К.
а) Согласно заданным координатам откладываем проекции точек в соответствии с установленными направлениями осей;
б) Каждая точка должна иметь три проекции.
Построить точки пересечения прямой I со сферой
а) Через прямую i в π2 проводим α2
в) Находим проекции точек в π1и проводим окружность R=1102
г) Окружность пересекает прямую I в точках 3 141
д) Определяем видимость
Возможно, вас также заинтересует эта ссылка:
Построить линию пересечения двух плоскостей, определить видимость линий
г) КМ – линия пересечения
д) Определяем видимость с помощью конкурирующих точек
Построить линию пересечения прямой с и плоскости, заданной параллельными прямыми a и b
а) Согласно заданным координатам откладываем проекции точек в соответствии с установленными направлениями осей;
б) Каждая точка должна иметь три проекции.
Разделить отрезок АВ точкой С в отношении АС:АВ=3:2
а) Через т. А2 проводим горизонталь h2 в плоскости π2, замечаем расстояние от т. В2 до горизонтали и в проекции π1 откладываем его на перпендикуляре отрезку А 1В1, получаем т. В’1, А1 В’1 – натуральная величина АВ.
б) На А1 В’1 откладываем равные между собой отрезки количеством 3+2=5; Соединяем В’1 с В1 и II В’1 В1 находим проекции равных по величине отрезков
в)Определяем положение. С1 на отрезке А 1В1 а заданной пропорции АВ:СВ=3:2
г) Находим проекцию т. С2 в π2
Построить точки пересечения полусферы с прямой а, показать видимость
а) Через прямую а2 в π2 проводим α2
б) α2∩ с полусферой по ее образующей
в) Находим проекции точек в π1 на горизонтальной оси полусферы и проводим окружность данным радиусом
г) Окружность пересекает прямую I в точках 1121, находим их проекции в π2
д) Определяем видимость
Определить расстояние от т. А до плоскости MNK
а) Проводим в π2 горизонталь h2 II оси х, замечаем точку 12, находим ее проекцию 11 в π1, проводим h1
б) Проводим в π1фронталь f1 II оси х, замечаем точку 21, находим ее проекцию 22 в π2, проводим f2
в) Опускаем перпендикуляр из т. А2 на f2
г) Опускаем перпендикуляр из т. А1 на h1
д) Заключаем перпендикуляр из т. А2 в плоскость α2
е) Плоскость α2 ∩ (MKN) = 32 42, находим их проекции в плоскости π1
з) Находим длину АВ, для этого в π1 замечаем длину перпендикуляра
А2 В2 = L (измерения производить перпендикулярно оси х)
и) В π2 перпендикулярно А2 В2 из т. А2 выводим перпендикуляр и откладываем длину L, получаем т. А02; длина В1 А01 – истинная величина перпендикуляра АВ.
Построить сечение пирамиды плоскостью, заданной фронталью и горизонталью
а) В плоскости π1 перпендикулярно h1 производим замену плоскости проекций π4; сносим проекции точек пирамиды и плоскости (h∩f)
в) Соединяем полученные точки получаем сечение 22 32 42 5 2
Построить точку пересечения прямой С с плоскостью, заданной пересекающимися прямыми а и b
а) В плоскости π1через прямую проводим плоскость α1, она засекает плоскость (a ∩ b) (ABS) в точках 1121, находим их проекции в π2
б) 1222∩ с2 =Р2 – точка пересечения прямой с и (a ∩ b)
а) Согласно заданным координатам откладываем проекции точек в соответствии с установленными направлениями осей;
б) Каждая точка должна иметь три проекции.
Способом замены плоскостей проекций определить истинную величину треугольника АВС
а) Проводим из т. С2 горизонталь h2 II оси х, на АВ замечаем т. 12, проецируем ее в π1, находим т. 11 на А1 В1
б) Перпендикулярно h1 в проекции С производим замену плоскости проекций π4
в) Проецируем точки АВС на π4 перпендикулярно оси х14 и отмечаем проекции точек согласно высотам в плоскости π2 соответственных точек
г) II А4 В4 С4 вводим плоскость π5 и проецируем перпендикулярно оси х45; точки А5 В5 С5, откладываем на расстоянии от точек А1 В1 С1 до х14
д) А5 В5 С5 – натуральная величина плоскости АВС
Построить проекции точки А, которая принадлежит плоскости β общего положения, заданной параллельными прямыми а и b
а)т.к. т. А принадлежит плоскости, заданной (a II b), то через т. А мы можем провести горизонталь h2 в π2; h2∩(a2 II b2)= 1222, находим их проекции в π1
б) из т. А2 опускаем проекционный луч в π1; пересечение луча и 1121 –искомая проекция т. А.
Построить линию пересечения плоскости, заданной пересекающимися прямыми a и b и прямыми с и d
а) Конусы в основании пересекаются в точках 1222, находим их проекции в π1
б) В π1проводим секущие плоскости II оси х12; данные плоскости пересекают два конуса; отмечаем радиусы пересечения и проецируем их на плоскость π2 на горизонтальную ось конусов; проводим окружности; пересечение окружностей, образованных сечением одной плоскости, дают точки пересечения двух конусов.
в) Соединяем получившиеся точки в π2 и проецируем их на соответствующие секущие плоскости в π1, соединяем линию пересечения
г) Определяем видимость
Построить линию взаимного пересечения поверхностей, определить видимость
а) Через две плоскости пропускаем секущие плоскости γ1; γ2
д) Находим проекции точек в π2
е) N D- линия пересечения плоскостей
Построить точку пересечения прямой с и плоскости, заданной параллельными прямыми а и b
б) Через проекцию прямой с2 (точка) проводим прямую и засекаем ее в плоскость α2; α2∩( a II b)= 1222; находим их проекции в π1-1121
в) 11 21 ∩ с1=S1— точка пересечения прямой и плоскости
Построить фронтальную проекцию кривой m, принадлежащей плоскости α
а)Выделяем на кривой m1 несколько ключевых точек: 21 31 41 5 1
б) Рассмотрим π1,проецируем точки кривой m1 на проекцию απ1 II оси х12 получаем точки 2’1 3’1 4’1 5’ 1и проецируем их на ось х12 получаем точки 2’2 3’2 4’2 5’ 2
б) II плоскости απ2 из проекций 2’2 3’2 4’2 5’ 2 проводим лучи, которые засекутся с проекционными лучами, выпущенными из точек 21 31 41 51, в проекциях точек 22 32 42 5 2
Способом замены плоскостей проекций определить истинную величину фигуры
а) Проводим из т. А2 горизонталь h2 II оси х, на СВ замечаем т. 12, проецируем ее в π1, находим т. 11 на С1 В1
б) Перпендикулярно h1 в проекции π1 производим замену плоскости проекций на π4
в) Проецируем точки АВС на π4 перпендикулярно оси х14 и отмечаем проекции точек согласно высотам в плоскости π2 соответственных точек
г) II А4 В4 С4 вводим плоскость π5 и проецируем перпендикулярно оси х45; точки А5 В5 С5, откладываем на расстоянии от точек А1 В1 С1 до х14
д) А5 В5 С5 – натуральная величина плоскости АВС
Определить расстояние от точки D до плоскости, заданной ∆АВС
а) Проводим в π2 горизонталь h2 II оси х, замечаем точку 12, находим ее проекцию 11 в π1, проводим h1
б) Проводим в π1фронталь f1 II оси х, замечаем точку 21, находим ее проекцию 22 в π2, проводим f2
в) Опускаем перпендикуляр из т. D2 на f2
г) Опускаем перпендикуляр из т. D1 на h1
д) Заключаем перпендикуляр из т. D2 в плоскость α2
е) Плоскость α2 ∩ (ABC) = 32 42, находим их проекции в плоскости π1
з) Находим длину DM, для этого в π2 замечаем длину перпендикуляра
D1 M1 = L (измерения производить перпендикулярно оси х)
и) В π1 перпендикулярно D1 M1 из т. D1 выводим перпендикуляр и откладываем длину L, получаем т. D01; длина M1 D01 – истинная величина перпендикуляра D M.
Построить точки пересечения прямой со сферой
а) Через прямую i2 в π2 проводим α2
б) α2∩ со сферой в точках 12 22 по образующей сферы, и в т. 32 в центральной т. проекции сферы
в) Находим проекции точек в π1 на горизонтальной оси сферы 1121 и 31, 3’1 в месте пересечения вертикальной оси и образующей сферы
д) Определяем видимость
Построить линию пересечения конуса и полусферы, определить видимость
а) Конус и сфера в π1 пересекаются в т. 1121; находим их проекции в π2
б) В π2 проводим секущие плоскости II оси х12; данные плоскости пересекают конус и сферу; отмечаем радиусы пересечения и проецируем их на плоскость π1 на горизонтальную ось конуса и сферы; проводим окружности; пересечение окружностей, образованных сечением одной плоскости, дают точки пересечения сферы и конуса.
в) Соединяем получившиеся точки в π1 и проецируем их на соответствующие секущие плоскости в π2, соединяем линию пересечения
г) Определяем видимость
Построить точку пересечения прямой а с плоскостью α
а) Проводим через прямую а в π2 горизонталь h2
б) из т. 11 II α π1 проводим луч, пересекающий прямую а в точке М 1 – точка пересечения а с плоскостью α
Построить третью проекцию точек и записать их координаты
а) Определяем существующие координаты точек с учетом индексов точек, заданных координатами осей x,y,z.
б) М(28, 15,15); С(-10;0;10); А(-22;30;-10); В(15;0;19)
Определить расстояние между точками А и В
а) Соединяем точки А и В в отрезок
а) Проводим горизонталь h2 через т. В2
б) Полученное расстояние от т. А2 до h2 откладываем на перпендикуляре от т. А1 в плоскости π1
Построить точки пересечения прямой L с конусом
Построить прямоугольную изометрию правильной пятиугольной пирамиды SABCDE
а) Строим аксонометрическую проекцию многогранника, оси х, y выполняются под углом 120 0 относительно оси z, величины принимаются 1:1
Построить точку пересечения прямой L с плоскостью ABC, определить видимость
а) Заключаем прямую L в плоскость α2
б) Она засекает т. 1 и 2 в π2, находим проекции точек в плоскости π1
г) Находим проекцию К2 в π2
д) Определяем видимость
Построить три проекции прямой А (0; 25;50), В (20;30;30), найти его натуральную величину
а) Согласно заданным координатам откладываем проекции точек в соответствии с установленными направлениями осей;
б) Находим третью проекцию прямой:
— откладываем значение y по горизонтали с правой стороны от оси z и находим проекции точек согласно фронтальным проекциям точек
в) Находим Н.В.- проводим в π2 из т. В2 горизонталь h2;
— полученное расстояние от т. А2 до h2 откладываем на перпендикуляре от т. А1 в π1;
Построить горизонтальную проекцию точки А, которая принадлежит плоскости, заданной прямой BC и точкой В
а) Определяем плоскость ВСD
б) Через т. А2 II оси х12 проводим горизонталь h2
в) h2 ∩ ВСD=12 22,находим их проекции на соответствующих сторонах плоскости ABCDи проводим горизонталь h1
г) т.к. горизонталь пропущена через т. А2, то проекция А1 будет лежать на горизонтали h1 и проекционном луче из т. А2.
Достроить горизонтальную проекцию четырехугольника ABCD
а) Для определения местоположения т. О следует в π2 провести диагонали четырехугольника АВСD
в) Через В1 и проводим прямую, засекающую т. D1 на проекционном луче из т. D2
Определить линию пересечения плоскостей, заданных пересекающимися прямыми с и d и а и b
а) Через две плоскости пропускаем секущие плоскости γ1; γ2
д) Находим проекции точек в π2
е) N D- линия пересечения плоскостей
Построить линию пересечения цилиндра и шара
а) Цилиндр и сфера в π1 пересекаются в т. 1121; находим их проекции 1222
в π2 на горизонтальной оси сферы
б) В π2 проводим секущие плоскости II оси х12; данные плоскости пересекают цилиндр и сферу; отмечаем радиусы пересечения и проецируем их на плоскость π1 на горизонтальную ось цилиндра и сферы; проводим окружности; пересечение окружностей, образованных сечением одной плоскости, дают точки пересечения сферы и конуса.
в) Соединяем получившиеся точки в π1 и проецируем их на соответствующие секущие плоскости в π2, соединяем линию пересечения
г) Определяем видимость
Построить точку пересечения прямой L с плоскостью ABC, определить видимость
а) Заключаем прямую L в плоскость α1
б) Она засекает т. 1 и 2 в π1, находим проекции точек в плоскости π2
г) Находим проекцию К1 в π1
д) Определяем видимость
Построить три проекции прямой А (50; 15;50), В (20;30;0), найти его натуральную величину
а) Согласно заданным координатам откладываем проекции точек в соответствии с установленными направлениями осей;
б) Находим третью проекцию прямой:
— откладываем значение y по горизонтали с правой стороны от оси z и находим проекции точек согласно фронтальным проекциям точек
в) Находим Н.В.- проводим в π2 из т. В2 горизонталь h2;
— полученное расстояние от т. А2 до h2 откладываем на перпендикуляре от т. А1 в π1;
Достроить горизонтальную проекцию многоугольника ABCDK и определить угол наклона плоскости к απ1
Построить сечение пирамиды плоскостью α
Построить точку пересечения прямой а с плоскостью α
а) Проводим через прямую а в π1 фронталь f1
б) f1 ∩ α π1=11, определяем проекцию 12 на оси х12
б) из т. 12 II α π2 проводим луч, пересекающий прямую а в точке А 2 – точка пересечения а с плоскостью α
Построить три проекции прямой А (10; 15;50), В (20;30;10), найти его натуральную величину
а) Согласно заданным координатам откладываем проекции точек в соответствии с установленными направлениями осей;
б) Находим третью проекцию прямой:
— откладываем значение y по горизонтали с правой стороны от оси z и находим проекции точек согласно фронтальным проекциям точек
в) Находим Н.В.- проводим в π2 из т. В2 горизонталь h2;
— полученное расстояние от т. А2 до h2 откладываем на перпендикуляре от т. В1 в π1;
Построить недостающую проекцию треугольника, лежащего в плоскости, заданной параллельными прямыми а и b
г) На проекционных лучах из т. А2 и С2 определяем проекции А1 и С1 на прямых 3111 и 2141
д) А1 В 1С1 – проекция треугольника в π1
Вращением вокруг оси i совместить точку K с плоскостью α
б) В π1 II плоскости απ1из т. 11 проводим луч
в) i – ось вращения, вращаем т. К1,до совмещения ее с лучом из т. 11, получаем т. К’1
г) Находим на пересечении проекционных лучей т К.
Построить линии пересечения цилиндра с конусом
а) Цилиндр и конус в π2 пересекаются в т. 1222; находим их проекции 1121
в π1 на горизонтальной оси цилиндра
б) В π2 проводим секущие плоскости II оси х12; данные плоскости пересекают цилиндр и конус; отмечаем радиусы пересечения и проецируем их на плоскость π1 на горизонтальную ось цилиндра и сферы; проводим окружности; пересечение окружностей, образованных сечением одной плоскости, дают точки пересечения сферы и конуса.
в) Соединяем получившиеся точки в π1 и проецируем их на соответствующие секущие плоскости в π2, соединяем линию пересечения
г) Определяем видимость
Построить линию пересечения двух плоскостей, определить видимость линий
г) КМ – линия пересечения
д) Определяем видимость с помощью конкурирующих точек
Построить точку пересечения прямой С с плоскостью, заданной пересекающимися прямыми а и b
а) В плоскости π2через прямую с2 проводим плоскость α2, она засекает плоскость (a ∩ b) в точках 1222, находим их проекции в π1
б) 1121∩ с1 =М2 – точка пересечения прямой с и (a ∩ b)
Построить три проекции прямой А (0; 5;50), В (10;30; 0), найти его натуральную величину
а) Согласно заданным координатам откладываем проекции точек в соответствии с установленными направлениями осей;
б) Находим третью проекцию прямой:
— откладываем значение y по горизонтали с правой стороны от оси z и находим проекции точек согласно фронтальным проекциям точек
в) Находим Н.В.- проводим в π2 из т. В2 горизонталь h2;
— полученное расстояние от т. А2 до h2 откладываем на перпендикуляре от т. В1 в π1;
Построить недостающую проекцию треугольника, лежащего в плоскости, заданной параллельными прямыми a и b
г) На проекционных лучах из т. А1 и С1 определяем проекции А2 и С2 на прямых 3212 и 2242
д) А2 В 2С2 – проекция треугольника в π2
Преобразовать чертеж так, чтобы отрезок АВ спроецировался в точку (применить способ замены плоскостей проекций)
а) Производим замену плоскости π1 на π4 II А1 В1
б) Находим проекции А4 В4 согласно высотам в плоскости π2
в) Производим замену плоскости π4 на π5 перпендикулярно отрезку А4В4; перпендикулярно оси х45 переносится проекция отрезка, проецирующаяся в точку (расстояния от оси х45 откладываются согласно расстоянию от отрезка до оси х14)
Построить линию пересечения призмы и конуса
а) Рассмотрим π1: находим середины сторон призмы: 11, 21, 31 и их проекции во фронтальной плоскости
б) Продливаем прямые S1 31; S1 21;S1 11 до пересечения с основанием конуса в т. 6 1,51,41 соответственно
г) Определяем точки пересечения данных прямых с проекциями середин отрезков призмы
д) Определяем линию пересечения призмы и конуса
Построить линию пересечения пирамиды с плоскостью
а) В плоскости π1 перпендикулярно h1 производим замену плоскости проекций π4; сносим проекции точек пирамиды и плоскости (h∩f)
в) Соединяем полученные точки получаем сечение 22 32 42 5 2
Построить точку пересечения прямой а с плоскостью α
а) Заключаем прямую a в плоскость β; α∩β=12
б) Находим проекцию точки 1 на плоскости π1
в) Проводим прямую а2 до пересечения с осью х, получаем т. 22
г) Находим проекцию т. 2 в плоскости π1
е) Определяем видимость.
Построить три проекции прямой А (40; 5;50), В (20;30; 0), найти его натуральную величину
а) Согласно заданным координатам откладываем проекции точек в соответствии с установленными направлениями осей;
б) Находим третью проекцию прямой:
— откладываем значение y по горизонтали с правой стороны от оси z и находим проекции точек согласно фронтальным проекциям точек
в) Находим Н.В.- проводим в π2 из т. В2 горизонталь h2;
— полученное расстояние от т. А2 до h2 откладываем на перпендикуляре от т. В1 в π1;
а) Согласно заданным координатам откладываем проекции точек в соответствии с установленными направлениями осей;
б) Каждая точка должна иметь три проекции.
Определить расстояние от т. А до плоскости CDE
а) Проводим в π2 горизонталь h2 II оси х, замечаем точку 12, находим ее проекцию 11 в π1, проводим h1
б) Проводим в π1фронталь f1 II оси х, замечаем точку 21, находим ее проекцию 22 в π2, проводим f2
в) Опускаем перпендикуляр из т. А2 на f2
г) Опускаем перпендикуляр из т. А1 на h1
д) Заключаем перпендикуляр из т. А2 в плоскость α2
е) Плоскость α2 ∩ (CDE) = 32 42, находим их проекции в плоскости π1
з) Находим длину АК, для этого в π1 замечаем длину перпендикуляра
А1 К1 = L (измерения производить перпендикулярно оси х)
и) В π2 перпендикулярно А2 К2 из т. А2 выводим перпендикуляр и откладываем длину L, получаем т. А02; длина К2А02 – истинная величина перпендикуляра А К.
Построить через точку А прямую, перпендикулярную прямой b
а) Производим замену плоскости π1 на π4 II b1
б) Находим проекции b4 и А4 согласно высотам в плоскости π2
в) Из т. А4 опускаем на b4 перпендикуляр – прямая m 4
Построить сечение конуса и цилиндра, определить видимость
а) Рассмотрим проекции тел вращения в π2:
— образующая конуса S2 K2 пересекает цилиндр в т. 12 и 22, проецируем точки на горизонтальную ось конуса, проходящую через вершину S, в плоскости π1;
б) В плоскости π2 проводим секущие плоскости α1, α2, α3, α4, данные плоскости пересекают и конус и цилиндр, находим общие точки пересечения, проецируем их в π1на соответствующие сечения плоскостями
в) Соединяем точки сечения
г) Определяем видимость
Возможно, вас также заинтересует эта ссылка:
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.










 Ответы на вопросы по заказу заданий по начертательной геометрии:
Ответы на вопросы по заказу заданий по начертательной геометрии:
























































































