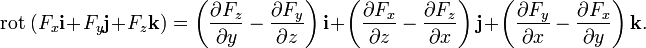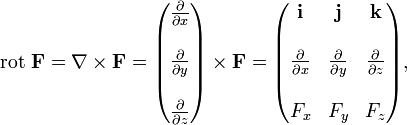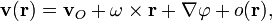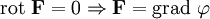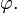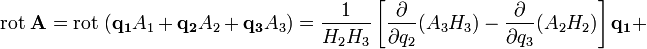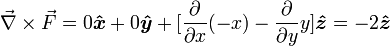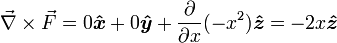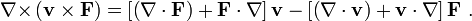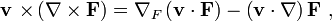Что такое ротор в математике
Ротор (матем.)
Ро́тор, или вихрь — векторный дифференциальный оператор над векторным полем. Показывает, насколько и в каком направлении закручено поле в каждой точке. Ротор поля F обозначается символом rot F (в русскоязычной литературе) или curl F (в англоязычной литературе), а также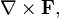 
где 
— векторный дифференциальный оператор набла.
Содержание
Математическое определение
Ротор векторного поля — вектор, проекция которого на каждое направление равна пределу отношения циркуляции векторного поля по контуру L плоской площадки ΔS, перпендикулярной к этому направлению, к величине этой площадки, когда размеры площадки стремятся к нулю, а сама площадка стягивается в точку:
.
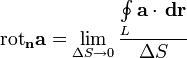
Нормаль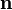 
к площадке направлена так, чтобы при вычислении циркуляции обход по контуру L совершался против часовой стрелки.
В трёхмерной декартовой системе координат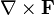 
вычисляется следующим образом:
Для удобства запоминания можно условно представлять ротор как векторное произведение:
где i, j и k — единичные орты для осей x, y и z соответственно.
Векторное поле, ротор которого равен нулю в любой точке, называется потенциальным (безвихревым).
Физическая интерпретация
По теореме Коши-Гельмгольца распределение скоростей сплошной среды вблизи точки О задаётся уравнением
где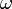 
— вектор углового вращения элемента среды в точке О, а 
— квадратичная форма от координат — потенциал деформации элемента среды.
Таким образом, движение сплошной среды вблизи точки О складывается из поступательного движения (вектор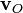 
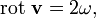
), вращательного движения (вектор 
) и потенциального движения — деформации (вектор 
). Применяя к формуле Коши—Гельмгольца операцию ротора, получим, что в точке О справедливо равенство 
и, следовательно, можно заключить, что когда речь идет о векторном поле, являющемся полем скоростей некоторой среды, ротор этого векторного поля в заданной точке равен удвоенному вектору углового вращения элемента среды с центром в этой точке.
Например, если в качестве векторного поля взять поле скоростей ветра на Земле, то в северном полушарии для антициклона, вращающегося по часовой стрелке, ротор будет направлен вниз, а для циклона, вращающегося против часовой стрелки — вверх. В тех местах, где ветры дуют прямолинейно и с одинаковой скоростью, ротор будет равен нулю (у неоднородного прямолинейного течения ротор ненулевой).
Основные свойства
Следующие свойства могут быть получены из обычных правил дифференцирования.
для любых векторных полей F и G и для всех вещественных чисел a и b.
При этом верно и обратное: если поле F бездивергентно, оно есть поле вихря некоторого поля G:
Верно и обратное: если поле безвихревое, то оно потенциально:
для некоторого скалярного поля 
Ротор (вектор)
Ро́тор, или вихрь — векторный дифференциальный оператор над векторным полем. Показывает, насколько и в каком направлении закручено поле в каждой точке. Ротор поля F обозначается символом rot F (в русскоязычной литературе) или curl F (в англоязычной литературе), а также 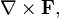где — векторный дифференциальный оператор набла.
Содержание
Математическое определение
Ротор векторного поля — вектор, проекция которого на каждое направление равна пределу отношения циркуляции векторного поля по контуру L плоской площадки ΔS, перпендикулярной к этому направлению, к величине этой площадки, когда размеры площадки стремятся к нулю, а сама площадка стягивается в точку:
.
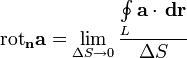
Нормаль 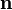к площадке направлена так, чтобы при вычислении циркуляции обход по контуру L совершался против часовой стрелки.
В трёхмерной декартовой системе координат 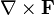вычисляется следующим образом:
Для удобства запоминания можно условно представлять ротор как векторное произведение:
где i, j и k — единичные орты для осей x, y и z соответственно.
Векторное поле, ротор которого равен нулю в любой точке, называется потенциальным (безвихревым).
Физическая интерпретация
По теореме Коши-Гельмгольца распределение скоростей сплошной среды вблизи точки О задаётся уравнением
где 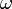— вектор углового вращения элемента среды в точке О, а — квадратичная форма от координат — потенциал деформации элемента среды.
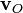
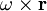
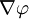
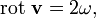
Таким образом, движение сплошной среды вблизи точки О складывается из поступательного движения (вектор ), вращательного движения (вектор ) и потенциального движения — деформации (вектор ). Применяя к формуле Коши—Гельмгольца операцию ротора, получим, что в точке О справедливо равенство и, следовательно, можно заключить, что когда речь идет о векторном поле, являющемся полем скоростей некоторой среды, ротор этого векторного поля в заданной точке равен удвоенному вектору углового вращения элемента среды с центром в этой точке.
Например, если в качестве векторного поля взять поле скоростей ветра на Земле, то в северном полушарии для антициклона, вращающегося по часовой стрелке, ротор будет направлен вниз, а для циклона, вращающегося против часовой стрелки — вверх. В тех местах, где ветры дуют прямолинейно и с одинаковой скоростью, ротор будет равен нулю (у неоднородного прямолинейного течения ротор ненулевой).
Основные свойства
Следующие свойства могут быть получены из обычных правил дифференцирования.
для любых векторных полей F и G и для всех вещественных чисел a и b.
При этом верно и обратное: если поле F бездивергентно, оно есть поле вихря некоторого поля G:
Верно и обратное: если поле безвихревое, то оно потенциально:
для некоторого скалярного поля
Ротор в ортогональных криволинейных координатах
Примеры
Простое векторное поле
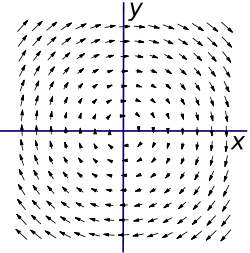
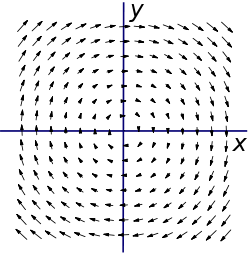
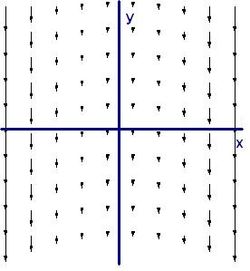
Рассмотрим векторное поле, линейно зависящее от координат x и y:
.
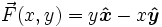
Очевидно, что поле закручено. Если мы поместим колесо с лопастями в любой области поля, мы увидим, что оно начнет вращаться по направлению часовой стрелки. Используя правило правой руки, можно ожидать ввинчивание поля в страницу. Для правой системы координат направление в страницу будет означать отрицательное направление по оси z.
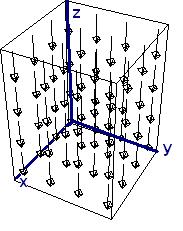
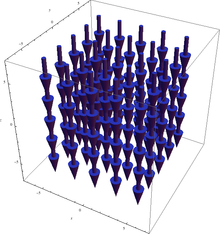
Как и предположили, направление совпало с отрицательным направлением оси z. В данном случае ротор является константой, так как он независим от координаты. Количество вращения в приведенном выше векторном поле одно и то же в любой точке (x,y). График ротора F не слишком интересен:
Более сложный пример
Теперь рассмотрим несколько более сложное векторное поле:
.
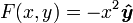
Три общих примера
Рассмотрим пример ∇ × [ v × F ]. Используя прямоугольную систему координат, можно показать, что
Если v и ∇ поменять местами:
что является фейнмановской записью с нижним индексом ∇F, что значит, что градиент с индексом F относится только к F.
Другой пример ∇ × [ ∇ × F ]. Используя прямоугольную систему координат, можно показать, что:
что можно считать частным случаем первого примера с подстановкой v → ∇.
Поясняющие примеры
Примечания
См. также
Полезное
Смотреть что такое «Ротор (вектор)» в других словарях:
РОТОР — (от лат. roto вращаю) (вихрь) одна из осн. операций векторногоанализа, сопоставляющая векторному полю а(r )др. векторное полеrot а (используются также обозначения curl а). Если точка r задана своими декартовыми координатами, а вектор а своими… … Физическая энциклопедия
Ротор (математика) — У этого термина существуют и другие значения, см. Ротор. Ротор, или вихрь векторный дифференциальный оператор над векторным полем. Обозначается (в русскоязычной[1] литературе) или (в англоязычной литературе), а также как векторное умножение … Википедия
Ротор (матем.) — Ротор, или вихрь векторный дифференциальный оператор над векторным полем. Показывает, насколько и в каком направлении закручено поле в каждой точке. Ротор поля F обозначается символом rot F (в русскоязычной литературе) или curl F (в англоязычной… … Википедия
Ротор векторного поля — Ротор, или вихрь векторный дифференциальный оператор над векторным полем. Показывает, насколько и в каком направлении закручено поле в каждой точке. Ротор поля F обозначается символом rot F (в русскоязычной литературе) или curl F (в англоязычной… … Википедия
Ротор поля — Ротор, или вихрь векторный дифференциальный оператор над векторным полем. Показывает, насколько и в каком направлении закручено поле в каждой точке. Ротор поля F обозначается символом rot F (в русскоязычной литературе) или curl F (в англоязычной… … Википедия
ВЕКТОР — В физике и математике вектор это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент,… … Энциклопедия Кольера
Ротор — Роторный экскаватор как экспонат в бывшем угольном карьере «стальном городе» Феррополис (Германия), превращенном в музей под открытым небом Ротор от лат. roto ) вращаться В математике: Ротор то же, что вихрь векторного поля, то… … Википедия
Ротор Дарье — У этого термина существуют и другие значения, см. Ротор. Ротор Дарье, турбина Дарье (Darrieus rotor) тип турбины низкого давления, ось вращения которой перпендикулярна потоку жидкой или газовой среды. Предложена в 1931 году французским… … Википедия
ротор — (лат. rotare вращать) 1) вращающаяся часть электрической машины (генератора или двигателя) внутри неподвижной части статора; 2) вращающаяся часть паровой турбины, компрессора, гидронасоса, гидромотора и т. д.; 3) несущий винт вертолета; 4) мат.… … Словарь иностранных слов русского языка
ротор — а, ч. 1) спец.Обертова частина машин, за допомогою якої енергія одного виду перетворюється в енергію іншого виду. 2) Гвинт вертольота. 3) мат. Вектор, який характеризує обертовий рух у даній точці векторного поля … Український тлумачний словник
Ротор (математика)
Ро́тор, или вихрь — векторный дифференциальный оператор над векторным полем. Показывает, насколько и в каком направлении закручено поле в каждой точке. Ротор поля F обозначается символом rot F (в русскоязычной литературе) или curl F (в англоязычной литературе), а также 
где — векторный дифференциальный оператор набла.
Содержание
Математическое определение
Ротор векторного поля — вектор, проекция которого на каждое направление равна пределу отношения циркуляции векторного поля по контуру L плоской площадки ΔS, перпендикулярной к этому направлению, к величине этой площадки, когда размеры площадки стремятся к нулю, а сама площадка стягивается в точку:
.
Нормаль к площадке направлена так, чтобы при вычислении циркуляции обход по контуру L совершался против часовой стрелки.
В трёхмерной декартовой системе координат вычисляется следующим образом:
Для удобства запоминания можно условно представлять ротор как векторное произведение:
или как определитель следующей матрицы:
где i, j и k — единичные орты для осей x, y и z соответственно.
Векторное поле, ротор которого равен нулю в любой точке, называется потенциальным (безвихревым).
Физическая интерпретация
По теореме Коши-Гельмгольца распределение скоростей сплошной среды вблизи точки О задаётся уравнением
где — вектор углового вращения элемента среды в точке О, а — квадратичная форма от координат — потенциал деформации элемента среды.
Таким образом, движение сплошной среды вблизи точки О складывается из поступательного движения (вектор ), вращательного движения (вектор ) и потенциального движения — деформации (вектор ). Применяя к формуле Коши—Гельмгольца операцию ротора, получим, что в точке О справедливо равенство и, следовательно, можно заключить, что когда речь идет о векторном поле, являющемся полем скоростей некоторой среды, ротор этого векторного поля в заданной точке равен удвоенному вектору углового вращения элемента среды с центром в этой точке.
Основные свойства
Следующие свойства могут быть получены из обычных правил дифференцирования.
для любых векторных полей F и G и для всех действительных чисел a и b.
При этом верно и обратное: если поле F бездивергентно, оно есть поле вихря некоторого поля G:
Верно и обратное: если поле безвихревое, то оно потенциально:
для некоторого скалярного поля
Ротор в ортогональных криволинейных координатах
Примеры
Простое векторное поле
Рассмотрим векторное поле, линейно зависящее от координат x и y:
.
Как и предположили, направление совпало с отрицательным направлением оси z. В данном случае ротор является константой, так как он независим от координаты. Количество вращения в приведенном выше векторном поле одно и то же в любой точке (x,y). График ротора F не слишком интересен:
Более сложный пример
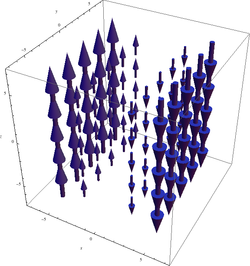
Теперь рассмотрим несколько более сложное векторное поле:
.
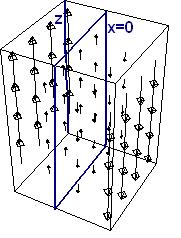
Ротор F с плоскостью x=0, выделенной темно-синим цветом
Три общих примера
Рассмотрим пример ∇ × [ v × F ]. Используя прямоугольную систему координат, можно показать, что
Если v и ∇ поменять местами:
что является фейнмановской записью с нижним индексом ∇F, что значит, что градиент с индексом F относится только к F.
Другой пример ∇ × [ ∇ × F ]. Используя прямоугольную систему координат, можно показать, что:
что можно считать частным случаем первого примера с подстановкой v → ∇.
Поясняющие примеры
Примечания
См. также
Ротор (математика)
Ро́тор, или вихрь — векторный дифференциальный оператор над векторным полем.
Результат действия этого оператора на конкретное векторное поле F называется ротором поля F или, короче, просто ротором F и представляет собой новое векторное [2] поле:
Поле rot F (длина и направление вектора rot F в каждой точке пространства) характеризует в некотором смысле [3] вращательную составляющую поля F соответственно в каждой точке.
Содержание
Интуитивный образ
Эта аналогия может быть сформулирована вполне строго (см. ниже). Основное определение через циркуляцию (данное в следующем параграфе) можно считать эквивалентным полученному таким образом.
Математическое определение
Ротор 
векторного поля 
— есть вектор, проекция которого 
на каждое направление n есть предел отношения циркуляции векторного поля по контуру L, являющемуся краем плоской площадки ΔS, перпендикулярной этому направлению, к величине этой площадки, когда размеры площадки стремятся к нулю, а сама площадка стягивается в точку:
.
(что можно считать альтернативным определением, по сути совпадающим с определением в начале параграфа, по крайней мере при условии дифференцируемости компонент поля).
Для удобства можно формально представлять ротор как векторное произведение оператора набла (слева) и векторного поля:
(Последнее равенство формально представляет векторное произведение как определитель).
Связанные определения
Векторное поле, ротор которого равен нулю в любой точке, называется безвихревым и является потенциальным. Поскольку эти условия являются друг для друга необходимыми и достаточными, оба термина являются практическими синонимами. (Впрочем, это верно только для случая полей, определённых на односвязной области).
Напротив, поле, ротор которого не равен нулю, называется обычно вихревым, такое поле не может быть потенциальным.
Обобщение
Наиболее прямое обобщение ротора применительно к векторным (и псевдовекторным) полям, определённым на пространствах произвольной размерности (при условии совпадения размерности пространства с размерностью вектора поля) такое
при индексах m и n от 1 до размерности пространства.
Это же может быть записано как внешнее произведение:
Физическая интерпретация
По теореме Коши-Гельмгольца распределение скоростей сплошной среды вблизи точки О задаётся уравнением
где 
— вектор углового вращения элемента среды в точке О, а 
— квадратичная форма от координат — потенциал деформации элемента среды.
Таким образом, движение сплошной среды вблизи точки О складывается из поступательного движения (вектор 
), вращательного движения (вектор 
) и потенциального движения — деформации (вектор 
). Применяя к формуле Коши—Гельмгольца операцию ротора, получим, что в точке О справедливо равенство 
и, следовательно, можно заключить, что когда речь идет о векторном поле, являющемся полем скоростей некоторой среды, ротор этого векторного поля в заданной точке равен удвоенному вектору углового вращения элемента среды с центром в этой точке.
В качестве интуитивного образа, как это описано выше, здесь можно использовать представление о вращении брошенной в поток маленькой пылинки (увлекаемой потоком с собой, без его заметного возмущения) или о вращении помещённого в поток с закреплённой осью маленького (без инерции, вращаемого потоком, заметно не искажая его) колеса с прямыми (не винтовыми) лопастями. Если то или другое при взгляде на него вращается против часовой стрелки, то это означает, что вектор ротора поля скорости потока в данной точке имеет положительную проекцию в направлении на нас.
Основные свойства
Свойства, непосредственно получаемые из обычных правил дифференцирования
для любых векторных полей F и G и для любых постоянных чисел a и b.
При этом верно и обратное: если поле F бездивергентно, оно вихрь некоторого поля G (векторного потенциала):
Верно и обратное: если поле безвихревое, то оно потенциально:
для некоторого скалярного поля 
(то есть найдется такое , что F будет его градиентом).
Теорема Стокса
Циркуляция вектора по замкнутому контуру, являющемуся границей некоторой поверхности, равна потоку ротора этого вектора через эту поверхность:
Альтернативные определения
Все определения ротора, о которых будет говориться в данном параграфе полностью эквивалентны (по крайней мере для случая дифференцируемого векторного поля), и в качестве основного, в принципе, можно выбрать любое из них. Остальные тогда оказываются формулами, которые могут быть более удобны в том или ином случае.
Прежде всего, перечислим явно те варианты, которые уже упоминались в статье выше и могут при желании каждое играть роль определения ротора.
Кроме них полезно упомянуть:
Ротор в криволинейных координатах
Общий случай
Удобным общим выражение ротора, пригодным для произвольных криволинейных координат в трехмерном [6] пространстве является выражение с использованием тензора Леви-Чивиты:
Используя верхние и нижние индексы и правило суммирования Эйнштейна:
где 
— координатная запись тензора Леви-Чивиты, включая множитель 
— метрический тензор в представлении с верхними индексами, 
Это выражение при желании может быть также переписано, например, в виде:
В ортогональных криволинейных координатах
Примеры
Простой пример
Рассмотрим векторное поле F, зависящее от координат x и y так:
Как и предположили, направление совпало с отрицательным направлением оси z. В данном случае ротор оказался константой, то есть поле 
оказалось однородным, не зависящим от координат (что естественно для вращения твёрдого тела). Что замечательно,
Угловая скорость вращения в данном примере одна и та же в любой точке пространства (угол поворота пылинки, приклеенной к твердому телу не зависит от того места, где именно приклеить пылинку). График ротора F поэтому не слишком интересен:
Более сложный пример
Теперь рассмотрим несколько более сложное векторное поле [7] :
.
Три общих примера
Рассмотрим пример ∇ × [ v × F ]. Используя прямоугольную систему координат, можно показать, что
Если v и ∇ поменять местами:
что является фейнмановской записью с нижним индексом ∇F, что значит, что градиент с индексом F относится только к F.
Другой пример ∇ × [ ∇ × F ]. Используя прямоугольную систему координат, можно показать, что:
что можно считать частным случаем первого примера с подстановкой v → ∇.
Поясняющие примеры
Важный контринтуитивный пример
Довольно важно иметь в виду, что в принципе (хотя и далеко не всегда) направление ротора может не соответствовать направлению вращения поля (будем говорить для конкретности о поле скоростей жидкости), которое кажется очевидным по направлению искривления линий тока. Он может даже иметь противоположное направление (а в частном случае ротор может оказаться равным нулю, хотя линии тока загибаются или даже представляют собой точные окружности).
Дело в том, что ротор может быть представлен как сумма двух слагаемых, одно из которых завивит от кривизны линий тока, а второе от завивимости скорости течения от перпендикулярной (в данной точке) скорости течения координаты.
Пусть скорость движения по каждой такой окружности (равная абсолютной величине вектора v) зависит только от r :
Нам будет досаточно вычислить ротор только вдоль оси x. Для этого выразим v (его компоненты) через координаты вблизи оси x.
(Учитывая то, что вблизи оси x можем считать, что координата y 
что даст, если подставить сюда 
приведённые выше,
Таким образом, мы видим, что в принципе просто из того, куда закручены линии тока не очевидно, куда направлен ротор такого течения. То есть не очевидно, в какую сторону будут вращаться пылинки в таком потоке. Зато достаточно ясно, что если где-то есть очень резкое убывание v(r), то направление ротора в этом месте будет направоено против того, которое соответствует направлению закручивания линий тока.
Необходимо однако сделать две оговорки: