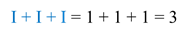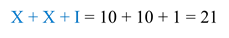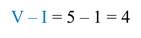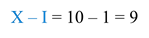Что такое ряд натуральных чисел 5 класс

Что такое Натуральное число

Определение натурального числа

Натуральные числа — это те числа, которые появились натуральным способом, когда считали сколько у человека есть предметов. Например: 1, 2, 3, 4, 5 и т. д.

Наибольшее натуральное число: не существует. Наименьшее натуральное число: 1.

Например, люди считали, сколько у них было фруктов: 1 яблоко, 3 апельсина, 2 дыни.

Нуль (0) не является натуральным числом, хотя некоторые области математики всё-таки считают 0 натуральным числом.

Отрицательные числа (–1, –3, –5. ) не являются натуральными числами («–3» яблок сложно посчитать физически).

Дроби (например, ⅓ или ⅖) тоже не являются натуральными числами.

Такие понятия, как отрицательные («–3»), дроби («⅓») и нуль («0») появились много позже.

Множество натуральных чисел

Множество натуральных чисел бесконечно и обозначается буквой N, т. е.:

Натуральные числа:

Натуральные числа с нулём:

Ряд натуральных чисел

Если записать все натуральные числа в порядке возрастания (каждое натуральное число отличается от предыдущего на 1), это будет ряд натуральных чисел. Но если какие-то числа будут отсутствовать, это уже не будет считаться рядом натуральных чисел. Например:

Наибольшего натурального числа не существует — натуральный ряд бесконечен.

Ненатуральные числа

Ненатуральные числа — это отрицательные и нецелые числа (обычно 0 тоже считается ненатуральным, но не всегда).

Отрицательные числа — это все те, которые ниже нуля, например: –1, –2, –3, –4, –5 и др.;

Свойства натуральных чисел

Натуральные числа обладают следующими свойствами:

Источник

Математика. 5 класс

Конспект урока

Ряд натуральных чисел. Десятичная система записи натуральных чисел

Перечень вопросов, рассматриваемых в теме:

— десятичная запись натуральных чисел;

— разрядность натуральных чисел

Натуральные числа – числа, которые используют при подсчёте предметов.

Натуральный ряд – последовательность всех натуральных чисел, расположенных в порядке возрастания.

Система счисления – это способ записи чисел с помощью заданного набора специальных знаков (цифр).

Теоретический материал для самостоятельного изучения

С древних времен у человека была потребность в счёте.

Числа, которые используют при подсчёте предметов, называют натуральными числами.

Таким образом, числа: один, два, три, …, десять, …, сто, …, тысяча, …, миллион и так далее – это натуральные числа.

Натуральные числа один, два, три, четыре, пять и так далее, записанные в порядке возрастания и без пропусков, образуют ряд натуральных чисел.

Стоит отметить, что самое маленькое натуральное число – единица (1). В натуральном ряду каждое следующее число на 1 больше предыдущего. Натуральный ряд бесконечен, наибольшего числа в нём нет.

В настоящее время принята десятичная система записи чисел (десятичная система счисления), в которой числа записываются при помощи десяти знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 – эти знаки называют цифрами.

Одна и та же цифра может иметь различное значение в зависимости от позиции, где она расположена в записи числа. Например, в записи числа пятьсот пятьдесят пять первая справа цифра пять означает пять единиц, вторая – пять десятков, третья – пять сотен.

Вот поэтому десятичную систему счисления называют позиционной.

Натуральные числа, записанные одной цифрой, называют однозначными, а записанные несколькими цифрами – многозначными: двумя – двузначными, тремя – трёхзначными и т. д.

Например, числа 1, 8, 9 – однозначные числа; 10, 66, 89 – двузначные числа; 111, 145 – трёхзначные числа; 123456 – шестизначное число.

Для чтения многозначных чисел их разбивают, начиная справа, на группы по три цифры в каждой (самая левая группа может состоять из одной или двух цифр). Эти группы называются классами.

Первый класс справа называют классом единиц, второй – классом тысяч, третий – классом миллионов, четвёртый – классом миллиардов и т. д.

Источник

Натуральные числа и нуль

Видеоурок по этой теме можно посмотреть по ссылке: Натуральные числа и ноль.

Пройти тест по теме «Натуральные числа и действия над ними» можно по ссылке. Проверьте свои знания!

Нас повсюду окружают предметы. Так было раньше, и так будет всегда. И очень часто необходимо знать, сколько у нас или где-то еще есть тех или иных предметов: яблок, машин, людей, денег и т.д.

Еще в очень глубокой древности, когда не было не только науки математики, но и даже такого понятия как число, древние люди проводили подсчет при помощи наиболее близких для них инструментов – собственных частей тела: «Там столько буйволов, сколько на моих руках пальцев», или: «Мы поймали рыбы столько, сколько пальцев на руках у меня и тебя».

Со временем они заметили, что десять буйволов, десять рыб, десять врагов и т.д. объединяет то, что рассказывая об этом, люди употребляют одинаковое описание: «сколько на моих руках пальцев». То есть, они обнаружили, что группы разных предметов обладают одним схожим свойством – количеством, и что удобнее назвать одинаковое количество чего-либо обобщенным названием, которое будет определять эту величину. И вместо: «Мы поймали столько рыбы, сколько пальцев на моих руках» люди начали говорить: «Мы поймали десять рыб». Так появились числа, которые впоследствии были названы натуральными. Подробнее об истории возникновения чисел можно почитать по ссылке.

Натуральные числа – это те числа, при помощи которых мы осуществляем счет предметов: 1, 2, 3, 4, 5 и т.д

Число 1 (один) имеет еще одно название: единица.

Если к единице приложить еще единицу, к получившемуся результату еще одну, потом еще, и еще и т.д., то мы получим ряд натуральных чисел или просто натуральный ряд: один, два, три, четыре, пять и т.д.

Любое натуральное число можно представить в виде единицы или собрания нескольких единиц.

Начинается натуральный ряд чисел с единицы, то есть, с числа 1 (один).

Каждое последующее число ряда отличается от предыдущего на единицу.

Любое натуральное число больше нуля.

Нуль не относится к натуральному ряду чисел. В некоторых англоязычных странах его включают в этот ряд, но в отечественной математике принято по-другому. Действительно, нуль означает отсутствие чего-либо, «ни одной единицы», «ни одного», «ничего». А поскольку ряд натуральных чисел состоит из единицы и совокупности сложений единиц, то число «ни одной единицы» не может находиться в этом ряду.

Нуль обладает такими свойствами:

Источник

Обозначение натуральных чисел (натуральные числа, натуральный ряд)

Урок 1. Математика 5 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Обозначение натуральных чисел (натуральные числа, натуральный ряд)»

На этом уроке мы с вами узнаем такие понятия, как натуральные числа, число 0 (нуль), натуральный ряд. Поговорим о свойствах натуральных чисел. Рассмотрим виды систем счисления. А также обсудим знаки для записи системы счисления.

Человек выражает свои чувства, эмоции и отношение к чему-либо или к кому-либо с помощью слов. Все вы, обращаясь друг к другу, используете слова.

В математике также существует свой язык, и выявляется он не только словами, но и числами.

Натуральные числа – одно из старейших математических понятий. У древних людей кроме топора, сделанного из камня, и одежды из шкуры ничего не было, поэтому считать им было нечего. Со временем они стали приручать животных, обрабатывать поля, и появилась торговля.

Тут уж без счёта им стало не обойтись. Сначала считали на пальцах. Когда пальцев одной руки не хватало, переходили на пальцы второй руки, а если считать нужно было дальше и пальцев обеих рук не хватало, то переходили на пальцы ног.

Чисел очень много, поэтому математики разбили их на несколько групп. Самая маленькая из них – натуральные числа.

С помощью натуральных чисел мы можем говорить о количестве предметов, а также можем назвать порядковый номер во множестве предметов.

Вот, к примеру, давайте посчитаем, сколько яблок на картинке.

Одно, два, три, четыре, пять.

Сейчас мы говорили о количестве предметов.

А если вспомнить урок физкультуры, когда учитель просит вас рассчитаться в строю, то, наверняка, каждый из вас может без особого труда назвать свой номер.

Здесь мы уже говорим о порядковом номере каждого ученика в строю.

Числа, которыми мы с вами пользовались при счёте, называют натуральными числами.

Обозначают их латинской буквой .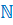

Натуральные числа также употребляют, чтобы выразить результаты измерения различных величин:

Кроме натуральных чисел мы знаем ещё число 0 (нуль). При счёте число нуль не используется, а означает оно «ни одного». Поэтому число 0 (нуль) не является натуральным!

С натуральными числами можно выполнять следующие арифметические действия: сложение, вычитание, умножение, деление, возведение в степень, извлечение корня.

Чтобы человек мог использовать натуральные числа, они должны быть каким-либо образом понятны нашему слуху, а также зрению.

Если озвучить каждое натуральное число, то оно станет слышно.

А если изобразить натуральное число, то его можно будет увидеть. Это самые простые способы воспринять натуральные числа.

Записывать числа люди научились гораздо позже, чем считать. Раньше всего они стали изображать 1 одной палочкой, 2 – двумя палочками, 3 – тремя палочками и так далее с остальными числами.

В Древней Греции поступали гораздо проще: греки не стали выдумывать специальные знаки для цифр, а использовали вместо них буквы.

1 обозначали буквой А, цифру 2 обозначали буквой Б и так далее с остальными числами.

Цифры, которыми мы пользуемся для записи чисел, родились в Индии несколько тысячелетий назад. В Европу их привезли арабы, поэтому их стали называть арабскими цифрами.

Однако в самой Индии до последнего времени цифры выглядели совсем не так, как в Европе. Затем появились и особые знаки для обозначения чисел — предшественники современных цифр.

Кстати, «нуль» по арабски – «сифр», откуда и пошло название «цифра».

Для счёта предметов используют натуральные числа. Любое натуральное число можно записать с помощью десяти цифр. Давайте назовём их:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Посмотрите, как мы записываем числа.

К примеру, число «пятьсот двадцать один» – 521.

Или «двадцать тысяч пятьсот» – 20 500.

Такой способ записи чисел, которым мы пользуемся, называется десятичной позиционной системой счисления. Числа в ней записываются с помощью десяти цифр. Значение цифры зависит от её места (позиции) в записи числа.

Возьмём, например, числа 250 и 502.

В первом числе цифра 5 обозначает количество десятков.

В записи числа 502 цифра 5 уже обозначает количество сотен.

Цифра 0 в записи обоих чисел указывает на отсутствие единиц в разряде.

Все натуральные числа, записанные по порядку (каждое число на своём месте), образуют натуральный ряд.

В натуральном ряду на первом месте стоит цифра 1, а каждое последующее число на единицу больше. Т. е., чтобы получить 2, мы должны к 1 + 1. Чтобы получить 3, мы точно так же будем к 2 + 1 и т. д.

Скажите, пожалуйста, до какого числа мы можем с вами посчитать? Назовите любое большое число. А какое число больше его на 1?

Получается, что самого последнего числа нет, т. к. к имеющемуся последнему числу можно прибавить единицу и снова получить новое последнее число. Перечисление натуральных чисел не имеет конца, и поэтому говорят, что натуральный ряд бесконечен. Весь натуральный ряд записать НЕВОЗМОЖНО! Поэтому поступают следующим образом: записывают подряд несколько последовательных чисел, начиная с 1, после чего ставят многоточие.

Первым натуральным числом является 1(единица), а вот последнего числа не существует.

Итак, теперь давайте выявим свойства натурального ряда.

Свойства натурального ряда:

1) наименьшее число натурального ряда – 1(один), наибольшего нет;

2) для каждого числа найдётся такое, которое больше его на 1;

3) для каждого числа, кроме 1, найдётся такое, которое меньше его на 1;

4) число 0 «нуль» не является натуральным, поскольку не используется при счёте.

Эти четыре правила нужно запомнить, поскольку они необходимы при решении многих задач.

Рассмотрим несколько примеров правильной записи натуральных чисел. Перед нами четыре числа:

Из приведённых примеров можно заметить, что для того чтобы записать натуральное число, не обязательно нужно использовать все из десяти цифр, а ещё цифры в записи числа могут повторяться. Вот, например, число 22: здесь цифра 2 повторяется.

Посмотрите на следующие записи чисел:

Они не являются записями натуральных чисел, т. к. слева находится цифра 0 (нуль). Запомните: запись натурального числа в десятичной системе счисления НЕ МОЖЕТ начинаться с нуля.

Помимо десятичной системы счисления существуют и другие. Например, в информатике используется двоичная позиционная система счисления.

А с шестидесятеричной системой счисления мы сталкиваемся, когда говорим об измерении времени.

Существуют и непозиционные системы счисления. Например, римская нумерация. В ней числа записываются с помощью римских цифр. Посмотрите, как обозначаются римские цифры:

Для записи римских чисел используются правила сложения и вычитания. Если меньшая цифра стоит после большей, то она прибавляется к большей, а если меньшая цифра стоит перед большей, то она вычитается из большей.

Посмотрите, как правильно называть число в римской нумерации.

Например, число ІІІ.

Здесь все цифры равноценны. Значит, мы будем просто складывать единицы:

В этом числе стоит на первом месте цифра 5. Она больше единичек, записанных после неё. Т. е. получаем, что меньшие цифры стоят после большей, а значит, мы будем прибавлять:

Посмотрим следующее число: XXI.

Здесь точно так же меньшая цифра стоит после больших. Значит, по правилам записи римских чисел будем складывать:

Следующее число: IV.

В этом числе меньшая цифра записана перед большей. Следовательно, мы должны от большего отнять меньшее:

Следующее число: IX.

Здесь точно так же меньшая цифра стоит перед большей. Значит, будем от большего числа отнимать меньшее:

Римскую нумерацию сейчас используют только для записи порядковых числительных. Так, например, запись «XXI в.» читают: «двадцать первый век». А запись «V класс» читают: «пятый класс».

Итак, на уроке мы познакомились с такими понятиями, как натуральные числа, число 0 (нуль), натуральный ряд, а также изучили свойства натурального ряда. Узнали, какие бывают системы счисления, с помощью каких знаков они записываются.

Источник

Конспект урока математики в 5 классе на тему: «Ряд натуральных чисел»

Урок №1 по математике в 5 классе.

Тема: Ряд натуральных чисел.

Тип урока: урок открытия новых знаний.

— деятельностная: развивать готовность и способность к выполнению норм и требований изучения предмета, научить детей применять новые способы действия: осуществлять сравнение,классификацию с заданным критерием.

-содержательная: дать определение натуральным числам, сформировать понятие предшествующее число, следующее число, уметь различать ситуации «от числа a до числа b» (включительно) и «между числами a и b».

— предметные: Познакомиться с понятиями ряд натуральных чисел; наименьшее натуральное число. Сформировать понимание, что ноль не натуральное число. Записывать последующие и предыдущие элементы натурального ряда.

— метапредметные УУД: Регулятивные: учитывать правило в планировании и контроле способа решения

осуществлять сравнение, сериализацию и классификацию с заданным критерием

учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве.

-личностные: Уметь контролировать процесс и результат учебной математической деятельности, уметь выбирать желаемый уровень математических результатов.

Оборудование: учебник, доска, презентация.

I.Организационный этап. Мотивация учебной деятельности учащихся. 2 мин.

II. Постановка темы и цели урока. 5 мин.

Знакомство с учебником.4 мин.

III. Изучение нового материала.10 мин.

I V. Первичное закрепление нового материала.7 мин.

V. Самостоятельная работа с самопроверкой. 10 мин.

VI. Домашнее задание.1 мин.

VII. Рефлексия учебной деятельности на уроке.3 мин.

I.Организационный этап. Мотивация учебной деятельности учащихся.

— Здравствуйте, ребята! Поздравляю вас с началом учебного года, с вступлением в 5 класс, и с нашим первым уроком математики в этом учебном году! Желаю вам успехов! Будьте настойчивыми, любознательными, внимательными, и тогда вы непременно добьётесь высоких результатов! Итак, мы начинаем.

II. Постановка темы и цели урока.

— Давайте вместе прочитаем стихотворение, а вы скажете мне, о чём оно, и что вы заметили интересного? По одному человеку по цепочке дети читают по две строчки.

Как-то раз один 1 пингвин

Заблудился среди льдин.

Вышел он на берег моря,

Видит – два 2 медведя спорят.

Три 3 лисенка под кустами

Машут рыжими хвостами.

То тропинке он пошел,

Четырех 4 ворон нашел.

Под горою пять 5 зайчат

Из морковки суп едят.

Шесть 6 мышат, затеяв пир,

Поделить не могут сыр.

Семь 7 хорошеньких опят

На сыром пеньке сидят.

Восемь 8 чаек прилетели,

На пингвина поглядели.

Девять 9 лошадей пингвина

Отвезли домой на льдину.

Десять 10 ярких звезд сверкают,

Ждут, пока их сосчитают

-О чем говорится в стихотворении? (о числах по порядку)

-Сколько всего цифр вы знаете? (10)

-Что можно записывать с помощью цифр? (разные числа)

— А как вы думаете, что мы сегодня будем изучать на уроке? (числа)

-Верно, мы сегодня будем говорить о числах, у которых есть своё название – натуральные. Давайте запишем число и тему урока в тетради. Ряд натуральных чисел.

— Итак, сегодня мы узнаем, какие числа называют натуральными, выполним упражнения с натуральными числами, а вначале познакомимся с учебником.

Знакомство с учебником.

Итак, у вас перед глазами учебник по математике С.Никольского. Откройте его, и посмотрите. В начале автор обращается к вам в приветственной статье, обратите внимание на условные обозначения. На стр. 270 есть оглавление. В нем указаны темы, которые вы будете изучать. Дома внимательно ещё раз ознакомьтесь с учебником, полистайте его страницы. Пусть эта книга станет для вас проводником в увлекательный мир математики.

III. Изучение нового материала.

-Откройте учебник на странице 5. Как называется глава 1? (Натуральные числа и нуль.)

-Прочтите, что вам предстоит при изучении главы 1? (один читает, остальные следят по учебнику)

— А теперь найдите в учебнике определение натуральных чисел и прочитайте его.

-Какое число в натуральном ряду стоит на первом месте?

-Назовите самое большое натуральное число.

-Почему такого числа нет? (потому что за каждым натуральным числом следует еще одно натуральное число, а за ним другое и так далее.)

Давайте ещё раз повторим, сколько всего цифр? (10)

-Что мы можем записывать с их помощью?(числа)

— Почему нуль не считают натуральным числом? (его не используют при счете)

А теперь запишем самое важное в тетрадь.

1,2,3,4,5,6,…..- натуральные числа.

1-наименьшее натуральное число.

Наибольшего натурального числа не существует.

0 не является натуральным числом.

I V. Первичное закрепление нового материала.

Работа с учебником: стр. 6 № 4,5,6 (устно)

Уч.с.6№ 4. а) Назовите число, которое следует в натуральном ряду за числом: 13, 276, 3590, 999 999.

б)Назовите число, которое предшествует в натуральном ряду
числу: 2, 74, 100, 3050, 438 109, 1 000 000.

Уч.с.6№ 5. Сколько чисел в натуральном ряду:

а) от 1 до 29; б) от 1 до 38; в) от 30 до 38; г) от 100 до 125?

Уч.с.6№ 6. Сколько чисел в натуральном ряду между числами:

а) 1 и 29 (27); в) 30 и 38 (7);

б) 1 и 38 (36); г) 100 и 125 (24)?

V. Самостоятельная работа с самопроверкой.

1.Запишите число, которое предшествует в натуральном ряду числу 345.

2. Какое число следует в натуральном ряду за числом 2049?

3.Сколько натуральных чисел расположено от 1 до 50?

4. Сколько натуральных чисел расположено между 1 и 50?

5.Найдите сумму всех натуральных чисел от 1 до 9.

-Вернемся к последнему заданию самостоятельной работы. Как вы находили сумму всех натуральных чисел от 1 до 9?

— Можно этот пример решить удобным способом, складывая попарно первое и последнее, второе и предпоследнее ….слагаемые. Полученные суммы всегда равны 10. А в серединке останется только 5. Итак 4 пары по 10 и плюс 5, получится 40+5=50.

Таким способом можно находить суммы большего количества чисел, стоящих в натуральном ряду.

Известный математик Карл Гаусс, когда учитель задал ему задание в школе найти сумму чисел от 1 до 100, быстро дал ответ. И вы дома по желанию можете убедиться в этом. Попробуйте.

Дополнительно по желанию: найти сумму чисел т 1 до 100.

— Какова была сегодня тема урока?

-Какие числа называют натуральными?

-Что значит ряд натуральных чисел? ( значит числа стоят друг за другом в порядке возрастания без пропусков)

— Наименьшее натуральное число?

-Наибольшее натуральное число?

— Нуль является натуральным числом? Почему?

Источник