Что такое сегментация изображения

Сегментация изображений

Сегментация изображения — задача поиска групп пикселей, каждая из которых характеризует один смысловой объект. В статистике эта проблема известна как кластерный анализ и является широко изученной областью с сотнями различных алгоритмов. В компьютерном зрении сегментация изображения является одной из старейших и широко изучаемых проблем.

В более ранних техниках используется расщепление и слияние регионов, что соответствует разделительным и агломерационным алгоритмам в литературе по кластеризации. Современные алгоритмы чаще оптимизируют некоторые глобальные критерии, такие как внутрирегиональная согласованность и межрегиональные длины границ.

Ниже будут рассмотрены два алгоритма — графо-ориентированная сегментация и метод нормализованных срезов. Первый из них является базовым алгоритмом сегментации, который прост и понятен в реализации, но медленный и результаты недостаточно хороши. Второй алгоритм является продвинутой версией первого со множеством эвристик. Что отражается, как на производительности, так и на результатах.

Содержание

Графо-ориентированная сегментация (англ. Graph-based segmentation) [ править ]

Для любого региона R, его внутренняя разница определяется как наибольшая мера отличия в минимальном остовном дереве региона,

Для любых двух соседних областей, по крайней мере, с одним смежным ребром, соединяющим их вершины, разность между этими регионами определяется как ребро минимального веса, соединяющее эти два региона,

Алгоритм объединяет любые две соседние области, разница которых меньше минимальной внутренней разности этих двух областей,

[math]MInt(R_1, R_2) = \min(Int(R_1) + \tau(R_1), Int(R_2) +\tau(R_2)),[/math]

На рисунке слева — исходное изображение, справа — сегментированное после применения данного алгоритма.

Метод нормализованных срезов (англ. Normalized cuts) [ править ]

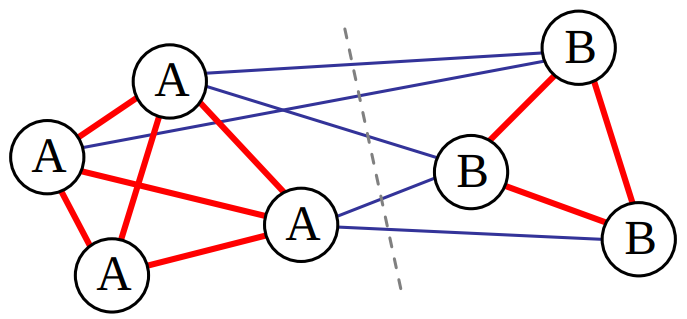
Mетод нормализованных срезов, исследует сходство между соседними пикселями и пытается разделить их на группы, которые в свою очередь связаны слабо. Рассмотрим простой пример.

Все пиксели в группе A имеют высокое сходство, показанное в виде толстых красных линий, как и пиксели в группе B. Соединения между этими двумя группами, показанные в виде более тонких синих линий, намного слабее. Нормализованный разрез между двумя группами, показанный пунктирной линией, разделяет их на два кластера.

Разрез между двумя группами A и B определяется как сумма всех взвешенных весов,

где веса между двумя пикселями [math]i[/math] и [math]j[/math] соответствуют их сходству. Однако использование минимального среза в качестве критерия сегментации не приводит к разумным кластерам, поскольку наименьшие срезы обычно предусматривают выделение одного пикселя.

Лучшей мерой сегментации является нормализованный срез, который определяется как

обычно [math]\phi = 0.2.[/math] Данный рисунок схематично показывает этот процесс.

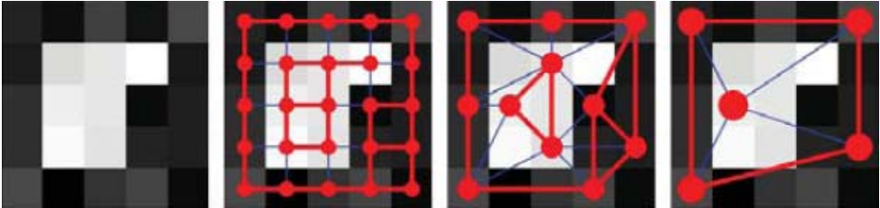
Так как количество вершин графа на втором изображении велико и работать с каждым из них чрезвычайно дорого, необходимо выделить подмножество вершин-предводителей для каждого из подмножеств и далее работать уже с ними. Мы начнем с выбора примерно половины пикселей в качестве представителей, которые назовем начальными числами: они выбираются таким образом, чтобы каждый пиксель в исходном изображении был сильно связан по крайней мере с одним соседним с ним начальным числом (см. третье изображение). Далее процесс продолжается рекурсивно (см. четвертое изображение), количество вершин на каждом новом более грубом уровне уменьшается. Значения узлов более нижнего уровня вычисляются путем интерполяции родительских значений и сопоставления значений [math] \epsilon = 0,1[/math] в пределах от 0 и 1 до Boolean значений. Выраженные сегменты появляются на соответствующем уровне как узлы, которые слабо связаны со своими соседями. Следовательно, задача минимизации упрощается до поиска вершин-предводителей на всех уровнях.

Результат работы данного алгоритма:

Свёрточные нейронные сети [ править ]

Модель U-Net, разработанная авторами для сегментации биомедицинских изображений, улучшает архитектуру FCN путём использования сужающихся блоков свёртки для захвата контекста, расширяющихся блоков свёртки для локализации, а также прямых связей между блоками свёртки на одинаковых уровнях. Прямая связь слоёв обеспечивает улучшенное обучение за счёт отсутствия так называемого «артефакта шахматной доски» — негативного явления, вызванного апсэмплингом при помощи транспонированной свёртки. Развитием U-Net, в свою очередь модель DenseNet, в которой используются полностью связанные свёрточные сети. В основе идеи лежит использование «плотных блоков» — совокупности нескольких свёрточных слоёв с подключением каждого слоя к каждому слою. Однако, существенным недостатком такой модели является низкая эффективность работы с памятью.

Совершенно по-иному на свёртку для сегментации объектов позволил взглянуть метод расширенных свёрток (англ. atrous convolutions), применяющийся в современных state-of-the-art подходах (DeepLab, DeepLab v3, DeepLab v3+). Расширенная свёртка заключается в том, чтобы применять свёртки с ядрами разного размера и разным страйдом над прямоугольниками с одним и тем же центром, а впоследствии комбинировать полученные таким образом признаки. Расширенные свёртки могут применяться как каскадно (последовательно регулируя показатель расширения фильтра), так и параллельно (англ. ASPP, Atrous Spatial Pyramid Pooling — применяя свёртки с различным масштабом ядер на одном и том же слое свёрточной сети с пулингом в конце). Такой подход позволил достичь лучших результатов в изображениях с объектами разных масштабов.

Источник

Эффективная сегментация изображений на графах

Сегментация изображений и выделение границ объектов (edge detection) играют важную роль в системах Computer Vision и применяются для задач распознавания сцен и выделения (определения) объектов. По большому счету, это такой же инструмент, как, например, сортировка, предназначенный для решения более высокоуровневых задач. И поэтому понимание устройства данного класса алгоритмов не будет лишним при построении подобных систем с учетом предъявляемых требований (в плане качество/производительность) и специфики поставленных задач.

В данной статье кратко описан алгоритм «Efficient Graph-Based Image Segmentation» авторов Pedro F. Felzenszwalb (MIT) и Daniel P. Huttenlocher (Cornell University), опубликованный в 2004 году. Да, алгоритм относительно старенький, но, несмотря на это, он до сих пор остается весьма популярным, демонстрируя неплохие результаты в плане производительности.

Под катом – большая смесь картинок и текста, не требовательная к текущему уровню знаний тематики. Любопытство приветствуется.

Сначала будет описан алгоритм на графах, на первый взгляд, имеющий мало общего с обработкой изображений. Однако чуть позже будет дана его интерпретация применительно к сегментации изображений.

Алгоритм Краскала

Алгоритм Краскала (wiki) строит каркас — минимальное остовное дерево данного графа. Далее будет использоваться английская аббревиатура MST (minimum spanning tree).

Задача: на карте расположено несколько населенных пунктов (на плате расположено несколько контактов), необходимо соединить все из них друг с другом таким образом, чтобы суммарная длина дорог (проводов) была минимальной.

* Да, задача в такой формулировке обычно называется «задачей Штейнера» (статья), решив которую, города можно соединить еще дешевле. Но нам-то, в конечном итоге, не асфальт укладывать… =)

Disjoint-set data structure

Допустим, на определенном шаге алгоритма попалось ребро, соединяющее два соседних пикселя: на одном конце ребра пиксель «оранжевый», а на другом «красный». Длину ребра определим как «разницу цвета» между пикселями. Все ребра меньшей длины (со схожим цветом) уже объединены: наверняка уже выделен оранжевый и красный сегмент попугайчика. Следуя алгоритму, нам нужно узнать, в одном ли сегменте лежат текущие «оранжевый» и «красный» пиксель? Если в разных, и мы считаем, что сегменты по цвету схожи, то объединяем их в один и продолжаем построение… В общем, тот же алгоритм Краскала, только с пикселями.

Отлично, теперь мы можем эффективно искать сегменты по пикселям и объединять их, а так же выстраивать MST по алгоритму Краскала. Пора узнать, как принимается решение о соединении или разделении двух областей.

Разделяй и властвуй

Алгоритм сегментации должен четко определять, где заканчивается один сегмент и начинается другой. Как правило, границы представляют собой характерные перепады яркости и/или оттенков цвета, встречающиеся на участках объект-фон, плоскость-тень, попугайчик-море, надпись на заборе… И если «перепад» больше некоторого «порога» (threshold), то из этого должно следовать, что это разные сегменты. Но есть небольшая проблемка: перепады могут сильно варьироваться для различных объектов, и сегменты сложно «отделить» однозначно заданной (const) пороговой величиной (threshold). Для поверхности стола на фоне стены: перепады соседних пикселей вдоль поверхности стола (стены) будут относительно небольшими, а вот на границе стол-стена будет скачок, который и разделит сегменты. Это ясно. А если у нас попугайчик на фоне моря? Он же сам очень «пестрый», внутри него большие перепады интенсивности (зеленый-красный-желтый-…), чтобы его «отделить» от моря, нужен другой «порог» (threshold). И постепенно приходим к выводу, что порог, который решает, что соседним сегментам «не суждено быть вместе», должен опираться не только на локальные показатели: перепад интенсивностей вдоль одного ребра (соединяющего соседние пиксели), но и на то, насколько эти сегменты сами по себе гладкие (в плане цвета) или «пестрые».

Серые картинки

Efficient Graph-Based Image Segmentation

В ходе выполнения алгоритма Краскала, на промежуточном этапе мы будем иметь несколько разрозненных сегментов (подмножеств пикселей), с минимальным суммарным весом ребер внутри: сегменты будут объединены ребрами минимальной длины, т.е. с минимальными «перепадами интенсивностей» между соседними пикселями. Поэтому соседние пиксели внутри одного сегмента будут схожи по цвету. Но только до некоторого значения максимального ребра (перепада интенсивности)…

Отдельно его искать не придется – достаточно просто сохранять длину ребра, добавляемого при объединении составляющих «подсегментов». Ведь на момент объединения длина добавляемого ребра была больше, чем в уже построенных MST каждого «подсегмента», т.к. ребра обрабатываются в возрастающем порядке.

Получаем примерное решающее правило для сегментов C₁, C₂ :

	Признак: следует ли разграничить эти сегменты
	Текущее ребро минимальной длины, соединяющее два разрозненных сегмента
	Меньший (из больших) перепад интенсивностей внутри одного из рассматриваемых сегментов

Получается что, для того чтобы сегменты «объединились», перепад интенсивностей на их границе должен быть меньше максимального перепада внутри каждого из объединяемых сегментов:

Ищу тебя

Однако, у такой формулировки расстояния есть недостаток. Если рассматривать «перепад интенсивности» между локально соседними пикселями, то небо на следующей картинке будет разбито на 2 отдельных сегмента проходящей поперек проволокой, или получим еще худший результат, если обработаем лужайку на фоне сетки:

Каждый фрагмент лужайки – будет отмечен как отдельный сегмент, но ведь это один объект!

Теперь пиксели будут считаться «соседями», если они расположены рядом, либо имеют схожий оттенок, хотя физически могут находиться на некотором удалении. Для построении графа авторы предлагают каждый пиксель соединять с 10 (20, 30) «ближайшими». Это дает более качественную сегментацию, но требует больше вычислительных ресурсов.

Stick together, team!

Возвращаясь в самое начало. Давным-давно, когда все пиксели были разрознены – между соседними мог наблюдаться существенный перепад интенсивностей, не позволяющий им объединяться (merge). Вряд ли нам предоставили микроскопическую фотографию, где каждый пиксель надо обособить — скорее всего, они являются частью какого-то большего объекта (попугайчика). Чтобы они поддавались «слиянию» (merge) в большей степени, чем уже построенные большие сегменты, для которых более важна корректность разбиения, в решающем правиле добавляют величину, зависящую от размера построенного сегмента: , где |C| – мощность рассматриваемого сегмента (количество пикселей в нем на текущий момент), а k – это уже параметр сегментации, задаваемый вручную. С подобной поправкой в решающем правиле будет использоваться формула:

«Поправка» постепенно нивелируется с ростом сегмента (увеличением |C| )…

На самом деле, вместо подобного задания T можно выбрать и иную функцию, учитывающую специфику обрабатываемых изображений: форму сегментов, положение на фотографии, определенные цветовые оттенки…

Размытие по Гауссу

Возвращаясь к очень «пестрым» картинкам:

Итого

Методов для сегментации существует много: различные подходы очень хорошо описаны в статье — «Методы сегментации изображений: автоматическая сегментация». А по большому счету, сегментация должна быть либо качественной, либо производительной, а если повезет – то все и сразу. Описанный выше метод представляет собой именно производительный вариант.

Исходный код алгоритма доступен по этой ссылке.

А как же OpenCV?

Во всеми любимой библиотеке OpenCV (wiki) есть метод «cvPyrSegmentation», т.е. пирамидальный метод сегментации изображений. Он устроен несколько иначе. Его описание заняло бы еще одну статью, поэтому — картинка. Сегменты строятся слоями (level), объединяя схожие по цвету пиксели в один (находящийся слоем выше), и далее последовательно обрабатывая слои находящиеся на следующем уровне (level) выше «до упора»:

В 2006 в Univesity of Malaga (Spain) было проведено сравнение нескольких пирамидальных алгоритмов и результаты изложены в следующей статье:

Авторы пришли к выводу, что из 8 методов, заслуживающими внимания являются 3, благодаря которым получаются достаточно качественные результаты разбиения изображения на объекты. Однако стоит отметить, что время выполнения пирамидальных алгоритмов колеблется от 0,5 сек. до 4,5 сек. (256×256 пикселей на Pentium 766 MHz), тогда как рассматриваемый «Efficient Graph-Based Image Segmentation» выполняется со слов авторов «in fraction of a second». У нас 1024×768 фотография отрабатывала за 0,5 сек (U9400 2 x 1.4GHz) внутри «матрешки»: VMWare – Matlab – mex (C++). В общем, пирамидальные – качество, описанные в статье графы – скорость. Оба имеют право на жизнь. =)

Самым усидчивым читателям, раскроем тайну «волшебных пузырьков»: что за цифры изображены на картинках? Это просто параметры метода «segmentation(sigma, k, min)«, с 2-мя из которых вы уже знакомы, а 3-ий «min» — это принудительно установленный минимальный размер сегмента, чтобы «маленьких» не оставалось.

Источник

Обзор алгоритмов сегментации

Алгоритм сегментации по водоразделам (WaterShed)

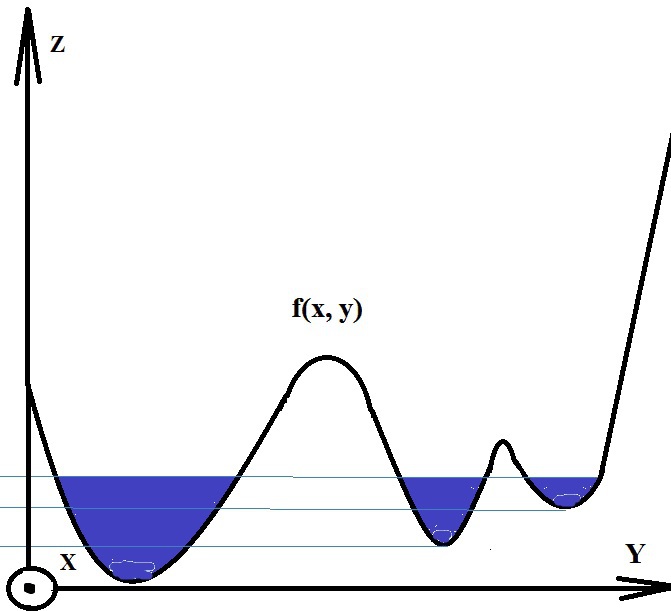
Алгоритм работает с изображением как с функцией от двух переменных f=I(x,y), где x,y – координаты пикселя:

Значением функции может быть интенсивность или модуль градиента. Для наибольшего контраста можно взять градиент от изображения. Если по оси OZ откладывать абсолютное значение градиента, то в местах перепада интенсивности образуются хребты, а в однородных регионах – равнины. После нахождения минимумов функции f, идет процесс заполнения “водой”, который начинается с глобального минимума. Как только уровень воды достигает значения очередного локального минимума, начинается его заполнение водой. Когда два региона начинают сливаться, строится перегородка, чтобы предотвратить объединение областей [2]. Вода продолжит подниматься до тех пор, пока регионы не будут отделяться только искусственно построенными перегородками (рис.1).

Рис.1. Иллюстрация процесса заполнения водой

Такой алгоритм может быть полезным, если на изображении небольшое число локальных минимумов, в случае же их большого количества возникает избыточное разбиение на сегменты. Например, если непосредственно применить алгоритм к рис. 2, получим много мелких деталей рис. 3.

Рис. 2. Исходное изображение

Рис. 3. Изображение после сегментации алгоритмом WaterShed

Чтобы избавиться от избытка мелких деталей, можно задать области, которые будут привязаны к ближайшим минимумам. Перегородка будет строиться только в том случае, если происходит объединение двух регионов с маркерами, в противном случае будет происходить слияние этих сегментов. Такой подход убирает эффект избыточной сегментации, но требует предварительной обработки изображения для выделения маркеров, которые можно обозначить интерактивно на изображении рис. 4, 5.

Рис. 4. Изображение с маркерами

Рис. 5. Изображение после сегментации алгоритмом WaterShed с использованием маркеров

Рис. 6. В качестве маркеров использовались контуры, имеющие длину выше определенного порога

В результате работы алгоритма мы получаем маску с сегментированным изображением, где пиксели одного сегмента помечены одинаковой меткой и образуют связную область. Основным недостатком данного алгоритма является использование процедуры предварительной обработки для картинок с большим количеством локальных минимумов (изображения со сложной текстурой и с обилием различных цветов).

Алгоритм сегментации MeanShift

MeanShift группирует объекты с близкими признаками. Пиксели со схожими признаками объединяются в один сегмент, на выходе получаем изображение с однородными областями.

Например, в качестве координат в пространстве признаков можно выбрать координаты пикселя (x, y) и компоненты RGB пикселя. Изобразив пиксели в пространстве признаков, можно заметить сгущения в определенных местах.

Рис. 7. (a) Пиксели в двухмерном пространстве признаков. (b) Пиксели, пришедшие в один локальный максимум, окрашены в один цвет. (с) — функция плотности, максимумы соответствуют местам наибольшей концентрации пикселей. Рисунок взят из статьи [3].

Чтобы легче было описывать сгущения точек, вводится функция плотности:
– вектор признаков i-ого пикселя, d — количество признаков, N — число пикселей, h — параметр, отвечающий за гладкость, — ядро. Максимумы функции расположены в точках сгущения пикселей изображения в пространстве признаков. Пиксели, принадлежащие одному локальному максимуму, объединяются в один сегмент. Получается, чтобы найти к какому из центров сгущения относится пиксель, надо шагать по градиенту для нахождения ближайшего локального максимума.

При выборе в качестве признаков координат пикселей и интенсивностей по цветам в один сегмент будут объединяться пиксели с близкими цветами и расположенные недалеко друг от друга. Соответственно, если выбрать другой вектор признаков, то объединение пикселей в сегменты уже будет идти по нему. Например, если убрать из признаков координаты, то небо и озеро будут считаться одним сегментом, так как пиксели этих объектов в пространстве признаков попали бы в один локальный максимум.

Если объект, который хотим выделить, состоит из областей, сильно различающихся по цвету, то MeanShift не сможет объединить эти регионы в один, и наш объект будет состоять из нескольких сегментов. Но зато хорошо справиться с однородным по цвету предметом на пестром фоне. Ещё MeanShift используют при реализации алгоритма слежения за движущимися объектами [5].

Результат:

Рис. 8. Исходное изображение

Рис. 9. После сегментации алгоритмом MeanShift

Алгоритм сегментации FloodFill

С помощью FloodFill (заливка или метод «наводнения») можно выделить однородные по цвету регионы. Для этого нужно выбрать начальный пиксель и задать интервал изменения цвета соседних пикселей относительно исходного. Интервал может быть и несимметричным. Алгоритм будет объединять пиксели в один сегмент (заливая их одним цветом), если они попадают в указанный диапазон. На выходе будет сегмент, залитый определенным цветом, и его площадь в пикселях.

Такой алгоритм может быть полезен для заливки области со слабыми перепадами цвета однородным фоном. Одним из вариантов использования FloodFill может быть выявление поврежденных краев объекта. Например, если, заливая однородные области определенным цветом, алгоритм заполнит и соседние регионы, то значит нарушена целостность границы между этими областями. Ниже на изображении можно заметить, что целостность границ заливаемых областей сохраняется:

Рис. 10, 11. Исходное изображение и результат после заливки нескольких областей

А на следующих картинках показан вариант работы FloodFill в случае повреждения одной из границ в предыдущем изображении.

Рис. 12, 13. Иллюстрация работы FloodFill при нарушение целостности границы между заливаемыми областями

Алгоритм сегментации GrabCut

Это интерактивный алгоритм выделения объекта, разрабатывался как более удобная альтернатива магнитному лассо (чтобы выделить объект, пользователю требовалось обвести его контур с помощью мыши). Для работы алгоритма достаточно заключить объект вместе с частью фона в прямоугольник (grab). Сегментирование объекта произойдет автоматически (cut).

Могут возникнуть сложности при сегментации, если внутри ограничивающего прямоугольника присутствуют цвета, которые встречаются в большом количестве не только в объекте, но и на фоне. В этом случае можно поставить дополнительные метки объекта (красная линия) и фона (синяя линия).

Рассмотрим идею алгоритма. За основу взят алгоритм интерактивной сегментации GraphCut, где пользователю надо поставить маркеры на фон и на объект. Изображение рассматривается как массив . Z — значения интенсивности пикселей, N-общее число пикселей. Для отделения объекта от фона алгоритм определяет значения элементов массива прозрачности , причем может принимать два значения, если = 0, значит пиксель принадлежит фону, если = 1, то объекту. Внутренний параметр содержит гистограмму распределения интенсивности переднего плана и гистограмму фона:
.
Задача сегментации — найти неизвестные . Рассматривается функция энергии:

Причем минимум энергии соответствует наилучшей сегментации.

V (a, z) — слагаемое отвечает за связь между пикселями. Сумма идет по всем парам пикселей, которые являются соседями, dis(m,n) — евклидово расстояние. отвечает за участие пар пикселей в сумме, если a _n = a _m, то эта пара не будет учитываться.
— отвечает за качество сегментации, т.е. разделение объекта от фона.

Найдя глобальный минимум функции энергии E, получим массив прозрачности . Для минимизации функции энергии, изображение описывается как граф и ищется минимальный разрез графа. В отличие от GraphCut в алгоритме GrabCut пиксели рассматриваются в RGB пространстве, поэтому для описания цветовой статистики используют смесь гауссиан (Gaussian Mixture Model — GMM). Работу алгоритма GrabCut можно посмотреть, запустив сэмпл OpenCV grabcut.cpp.

Мы рассмотрели только небольшую часть существующих алгоритмов. В результате сегментации на изображении выделяются области, в которые объединяются пиксели по выбранным признакам. Для заливки однородных по цвету объектов подойдет FloodFill. С задачей отделения конкретного объекта от фона хорошо справится GrabCut. Если использовать реализацию MeanShift из OpenCV, то пиксели, близкие по цвету и координатам, будут кластеризованы. WaterShed подойдет для изображений с простой текстурой. Таким образом, алгоритм сегментации следует выбирать, конечно, исходя из конкретной задачи.

Источник