Что такое секущая по отношению к 2 прямым

Что такое секущая по отношению двум прямым Назовите пары углов которые образуются при пересечении двух прямых и секущей?

Что такое секущая по отношению двум прямым Назовите пары углов которые образуются при пересечении двух прямых и секущей.

Прямая называется секущей по отношению к другим прямым, если она пересекает их в двух точках.

Накрест лежащие : 3 и 5 ; 4 и 6 ;

Односторонние : 4 и 5 ; 3 и 6 ;

Соответственные : 1 и 5 ; 4 и 8 ; 2 и 6 ; 3 и 7.

Ну а там по рисунку пары углов смотреть надо, я просто пример привела.

Назовите виды углов, образованные при пересечении двух прямых секущей?

Назовите виды углов, образованные при пересечении двух прямых секущей.

Докажите, что если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны?

Докажите, что если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Что такое секущая?

Назовите пары углов, которые образуются при пересечении двух прямых секущей.

Докажите что если при пересечении двух прямых секущей накрест лежащие углы равны то прямые параллельны?

Докажите что если при пересечении двух прямых секущей накрест лежащие углы равны то прямые параллельны.

Докажите, что если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны?

Докажите, что если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Что такое секущая?

Углы, образованные при пересечении двух прямых секущей?

Углы, образованные при пересечении двух прямых секущей.

Доказать что если при пересечении двух прямых секущей соответственные углы равны то прямые параллельны?

Доказать что если при пересечении двух прямых секущей соответственные углы равны то прямые параллельны.

Докажите что если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны?

Докажите что если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Докажите, если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны?

Докажите, если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Одна прямая бьёт плоскость на 2 части 2прямых 4 части. N прямых 2n частей.

Sin 45 = корень из 2 / 2.

Дано : сторона основания а = 8 см, угол наклонабокового ребра к плоскости основанияα = 30°. Находим высоту h основания : h = a * cos30° = 8√3 / 2 = 4√3 см. Проекция бокового ребра на основание равна : (2 / 3) * h = (2 / 3) * (4√3) = 8√3 / 3 см. Вы..

Докозательство не скажу, а так прямые не пересикаются.

Они будут пересекать, значит нет, если хоть одна из них не параллельная другой то они в любом случае пересекутся.

Источник

Что такое секущая по отношению к двум прямым?

Что такое секущая по отношению к двум прямым?

Назовите пары углов, которые образуются при пересечении двух прямых секущих.

Накрестлежащие, односторонние, соответственные.

Две параллельные прямые пересекаются секущей?

Две параллельные прямые пересекаются секущей.

Докажите, что биссектрисы двух внутренних односторонних углов перпендикулярны.

Найти все получившиеся при пересечении углы.

Найти все углы образованные при пересечении двух параллельных прямых а и в секущей с, если один из углов на 80° больше другого?

Найти все углы образованные при пересечении двух параллельных прямых а и в секущей с, если один из углов на 80° больше другого.

При пересечении двух параллельных прямых секущей разность односторонних углов равна 70 град?

При пересечении двух параллельных прямых секущей разность односторонних углов равна 70 град.

Найдите градусную меру большего угла.

Сколько прямых углов может образоваться при пересечении двух параллельных прямых секущей?

Сколько прямых углов может образоваться при пересечении двух параллельных прямых секущей.

Свойство односторонних углов при параллельных прямых и секущей?

Свойство односторонних углов при параллельных прямых и секущей.

Один из углов, полученных при пересечении двух параллельных прямых секущей, равен 50 градусам?

Один из углов, полученных при пересечении двух параллельных прямых секущей, равен 50 градусам.

Найдите наибольший из полученных углов.

Сумма накрест лежащих углов при пересечении двух паралельных прямых секущей равна 210 градусов Найдите эти углы?

Сумма накрест лежащих углов при пересечении двух паралельных прямых секущей равна 210 градусов Найдите эти углы.

Один из углов, которые получаются при пересечении двух паралельных прямых секущей равен 102 градуса?

Один из углов, которые получаются при пересечении двух паралельных прямых секущей равен 102 градуса.

Найдите остальные семь углов,

Решение смотри на фото.

Столько, сколько тебе лет. Ты же представляешь себя водителем.

Точно не сказать возраст, но точно больше 18(по правилам ПДД).

6 * (2√3)² = 6 * 2√3 * 2√3 = 6 * 2 * √3 * 2 * √3 = 6 * 4 * √9 = 6 * 4 * 3 = 72. ОТВЕТ : 72.

6(4 * 3) = 6 * 12 = 72 помоему так.

Источник

Геометрия. 7 класс

Конспект урока

Признаки параллельности прямых

Перечень рассматриваемых вопросов:

Две прямые на плоскости называются параллельными, если они не пересекаются.

Признаки параллельности двух прямых:

1. Если при пересечении двух прямых секущей, накрест лежащие углы равны, то прямые параллельны.

2. Если при пересечении двух прямых секущей, соответственные углы равны, то прямые параллельны.

3. Если при пересечении двух прямых секущей, сумма односторонних углов равна 180°, то прямые параллельны.

Теоретический материал для самостоятельного изучения.

Вы уже знаете, что при пересечении двух прямых секущей образуются углы:

Прямая c называется секущей по отношению к прямым a и b, если она пересекает их в двух точках.

Рассмотрим и докажем признаки параллельности прямых.

Если при пересечении двух прямых секущей, накрест лежащие углы равны, то прямые параллельны.

Дано: прямые a и b, секущая AB, ∠ 1 = ∠ 2 накрест лежащие.

В этом случае две прямые, перпендикулярные к третьей не пересекаются, т. е. параллельны.

2 случай: ∠ 1= ∠ 2 ≠ 90°

1) Из середины O отрезка AB проведём перпендикуляр OH к прямой а. На прямой b от точки B отложим отрезок BH₁, равный отрезку AH и проведем отрезок OH₁.

2) AO = OB т. к. O середина AB; AH = BH₁ по построению; ∠1 = ∠2 по условию. Тогда ΔOHA = ΔOH₁B по первому признаку равенства треугольников.

Далее следует из равенства треугольников: ∠3 = ∠4 и ∠5 = ∠6.

3) Из равенства углов ∠3 и ∠4 следует, что точка H₁ лежит на продолжении луча OH. Это значит, что точки H₁, O, H лежат на одной прямой.

4) Из равенства ∠5 и ∠6 следует, что ∠6 = 90°. Это значит, что прямые a и b перпендикулярны к третьей НН₁, а значит, по теореме о двух прямых, перпендикулярных к третьей, не пересекаются, т. е. параллельны.

Если при пересечении двух прямых секущей, соответственные углы равны, то прямые параллельны.

Дано: прямые a и b, секущая AB, ∠1 = ∠2 соответственные.

∠1 = ∠2 – по условию и ∠2 = ∠3 – по свойству вертикальных углов.

Значит, ∠1 = ∠3, это накрест лежащие углы, следовательно, a║b по теореме 1.

Если при пересечении двух прямых секущей, сумма односторонних углов равна 180°, то прямые параллельны.

Прямые a и b, секущая AB, ∠1 + ∠2 = 180° ‑ односторонние.

∠3 +∠2 = 180°– по свойству смежных углов, откуда ∠3 = 180° – ∠2.

∠1 + ∠2 = 180 ° по условию, откуда ∠1 = 180° – ∠2.

Тогда ∠1 = ∠3, это накрест лежащие углы, следовательно, a║b по теореме 1.

Разбор заданий тренировочного модуля.

Ответ: прямые a и b параллельны по 1 признаку параллельности прямых.

Дано: ΔABC – равнобедренный, ∠А = 60°. CD – биссектриса ∠BCK.

Ответ: AB║CD по 2 признаку параллельности прямых.

Источник

Секущая прямая

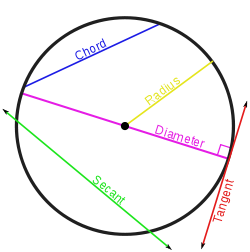
Секущая — это прямая, которая на некотором участке пересекает в двух точках данную кривую.

Путём приближения из секущей можно получить касательную в некоторой точке P. Если секущая определяется двумя точками пересечения с данной кривой, P и Q, где положение точки P фиксировано, а положение точки Q может изменяться, то по мере того, как точка Q приближается к точке P вдоль кривой, направление секущей приближается к направлению касательной в точке P (считаем, что первая производная кривой является непрерывной в точке P, и поэтому существует только одна касательная в этой точке). Можно сказать, что по мере того, как точка Q приближается к P, наклон секущей, или направление, в пределе приближается к наклону касательной. Эта идея является основой для геометрического определения производной.

Хорда — это участок секущей, который лежит между двумя точками пересечения с кривой.

См. также

Ссылки

Полезное

Смотреть что такое «Секущая прямая» в других словарях:

секущая — прямая Словарь русских синонимов. секущая сущ., кол во синонимов: 1 • прямая (6) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

прямая — биссектриса, параллель, линия, секущая, хорда, директриса Словарь русских синонимов. прямая сущ., кол во синонимов: 6 • биссектриса (3) • … Словарь синонимов

СЕКУЩАЯ — СЕКУЩАЯ, ей, жен. В математике: прямая, пересекающая кривую. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

СЕКУЩАЯ — всякая прямая, имеющая с кривой линией по меньшей мере две общие точки. Отрезок секущей, лежащий внутри окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром … Большая политехническая энциклопедия

Секущая — ж. Прямая линия, пересекающая кривую в двух или более точках. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой

секущая — ой; ж. Матем. Прямая, пересекающая кривую в двух или более точках … Энциклопедический словарь

секущая — ой; ж.; матем. Прямая, пересекающая кривую в двух или более точках … Словарь многих выражений

Секанс — [лат. secans, здесь секущая (прямая); от seco режу, рассекаю], одна из тригонометрических функций (См. Тригонометрические функции); обозначение sec. В прямоугольном треугольнике С. острого угла называют отношение гипотенузы к катету,… … Большая советская энциклопедия

СЕКАНС — [лат. secans, здесь: секущая (прямая), от seco режу, рассекаю] одна из тригонометрических функций … Большой энциклопедический политехнический словарь

Касательная — прямая, с которою стремится совпасть секущая, проведенная через две точки на произвольной кривой по мере сближения этих точек. Математическая теория К. имеет весьма важное значение (см. Дифференциальное исчисление). Точка, через которую к кривой… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Источник