Что такое силлогизм определение кратко

Значение слова «силлогизм»

Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

СИЛЛОГИ’ЗМ, а, м. [греч. syllogismos] (филос.). В формальной логике — умозаключение, в к-ром из двух ранее установленных суждений, называемых посылками, получается третье суждение, называемое выводом.

Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека

силлоги́зм

1. книжн. логическое заключение, сделанное из двух посылок ◆ Возьмём два факта: «Сократ — человек» и «Все люди смертны». Силлогизмом этих двух фактов будет «Сократ смертен».

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.

Насколько понятно значение слова изуверский (прилагательное):

Источник

Силлогизм

Силлогизм — это вид рассуждения, в котором две посылки, связывающие субъекты (подлежащие) и предикаты (сказуемые), объединены общим (средним) термином, обеспечивающим замыкание понятий (терминов) в заключении. В традиционной формальной логике (см. Логика) силлогизмом называют дедуктивное умозаключение, в котором из двух ранее установленных суждений (см. Суждение), называемых посылками, получается третье суждение, называемое выводом. Наряду с этим термин «силлогизм» применяется и в более широком смысле — применительно к условным и условно-категорическим умозаключениям, разделительно-категорическим умозаключениям и условно-разделительным (лемматическим) умозаключениям.

Впервые теория силлогизмов (силлогистика) была построена Аристотелем, который также сформулировал основной принцип силлогизма: «Когда одно сказывается о другом, как о подлежащем, то всё, что говорится о сказуемом, будет говориться и о подлежащем». Система Аристотеля послужила отправным пунктом для разработки формальной логики и при этом была не только первой логической теорией, но и одной из первых известных в истории науки (см. Наука) теорий (см. Теория) вообще.

Наиболее известной и хорошо исследованной в логике ещё со времён Аристотеля и схоластов разновидностью силлогизма является простой категорический силлогизм. Посылки и заключение последнего — ассерторические (то есть немодальные) атрибутивные высказывания, которые также называют категорическими.

Классическим примером простого категорического силлогизма является следующее умозаключение:

В простом категорическом силлогизме содержатся три термина:

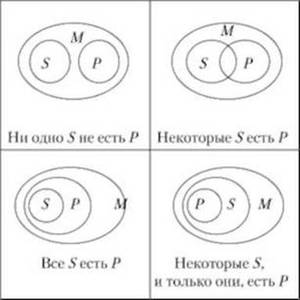
Термины силлогизма попарно связаны в высказываниях посредством одного из следующих четырёх логических отношений: «Всякое… есть…», «Ни одно… не есть…», «Некоторое… есть…», «Некоторое… не есть…».

Подлежащие S (субъект) — то, относительно чего мы высказываем (делится на два вида):

Сказуемое P (предикат) — то, что мы высказываем (два вида суждений):

Отношение между подлежащим и сказуемым:

При определении отношения между подлежащим и сказуемым важна чёткая формализация терминов.

Различают четыре вида простых атрибутивных высказываний, которые получили специальные обозначения:

Для условного буквенного обозначения высказываний здесь используются гласные из латинских слов affirmo (я утверждаю, говорю да) и nego (я отрицаю, говорю нет). Эти обозначения оказались удобным средством сокращённого представления в языке ассерторических и модальных высказываний.

Для характеристики соотношения объёмов субъекта и предиката используется понятие «распределённость термина». Термин считается распределённым, если его объём полностью включается в объём другого термина или полностью исключается из него. Термин считается нераспределённым, если его объём лишь частично включается в объём другого термина или частично исключается из него. Распределённость терминов силлогизма имеет следующие правила:

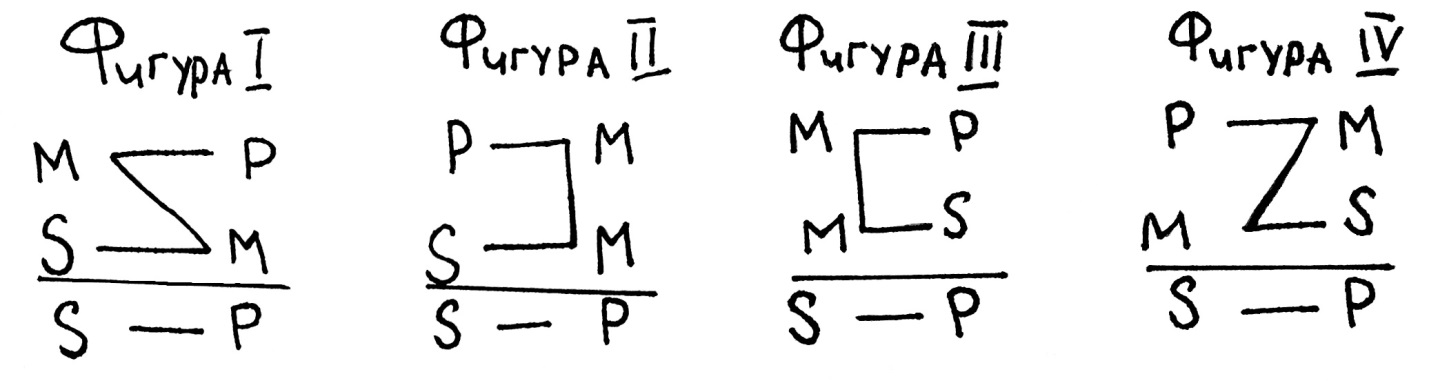
Согласно указанным условиям силлогизмы делятся на так называемые фигуры, которые представляют собой множество простых категорических силлогизмов, имеющих одну и ту же структуру, определяемую расположением среднего термина в посылках. С точностью до порядка посылок выделяют следующие фигуры силлогизмов:

Каждой фигуре соответствуют модусы, различающиеся в зависимости от логических отношений, связывающих термины в высказываниях силлогизма. Модусом простого силлогизма называется набор простых суждений, входящих в силлогизм.

Модус простого силлогизма составляет три суждения.

Имеет модус ААА (здесь первая посылка — это тоже простое суждение вида A, и вывод в данном случае представляет собой простое суждение вида A).

Во всех четырёх фигурах силлогизмов насчитывается 256 модусов. В каждой фигуре насчитывается 64 модуса. Однако из всех этих 256 модусов только 24 дают достоверные выводы. Это те модусы, для которых между посылками и заключением существует отношение логического следования (см. Логическое следование). Эти 24 модуса называются правильными. Остальные модусы приводят к вероятностным выводам и называются, соответственно, неправильными.

В традиционной силлогистике для 24 правильных модусов каждой фигуры имеются мнемонические имена. В этих названиях (см. таблицу ниже) гласные буквы слева направо указывают тип большей, меньшей посылок и заключения.

Правильные модусы различных фигур имеют следующие свойства:

Существуют несколько методов проверки силлогизмов. Аристотель и его средневековые последователи постулировали логическую корректность модусов первой фигуры, правильные модусы других фигур обосновывались посредством сведéния к модусам первой фигуры с использованием процедур обращения высказываний, перестановки посылок, законов логического квадрата и рассуждения от противного. Семантическая проверка силлогизма осуществляется с помощью объёмных диаграмм — кругов Эйлера.

В традиционной логике для проверки правильности рассуждений, строящихся в форме простого категорического силлогизма, сформулирован специальный перечень правил. Выполнение каждого правила является необходимым, а всех вместе — достаточным условием, чтобы считать некоторый модус правильным. Эти правила называются общими правилами силлогизмов и подразделяются на правила терминов и правила посылок.

Источник

Что такое силлогизм: описание и виды

Что такое силлогизм? Силлогизм – это особая форма мышления и единственно верный сделанный вывод. Конкретика следующая: во время познания становится ясно, что утверждения, очевидно подсказанные, не всегда являются истиной, а только их некоторая часть.

Для определения полной истины, как правило, выполняется тщательное расследование: конкретно обозначаются вопросы, соотносятся между собой уже определенные истины, собираются дополнительно требуемые факты, попутно проверяются все появляющиеся догадки и выводится конечный результат. Этим и является силлогизм или умозаключение.

В логике форма мышления происходит по-другому: из истинных фактов – одной или нескольких истин, – при выполнении ряда правил выведения результата формируется следующая, новая истина, непосредственно вытекающая из предыдущих.

Суть силлогизма

Итак, что такое силлогизм или умозаключение и какова его структура? Структура состоит из посылок (суждений), нового суждения (заключения) и логического умозаключения между посылками и заключением. Логические правила, с помощью которых появляется заключение, указывают на логическую взаимосвязь. Говоря иначе, какое-либо умозаключение состоит из сложных или простых суждений, оснащающие мозг новыми знаниями. Данные суждения в случае, когда признаются истинными и рождают новое, обобщают умозаключение.

Суждение же, которое получено с помощью обработки посылок, когда поработали методы силлогизма, называется выводом (логическим следствием или заключением). Рассмотрим, каким образом связаны между собой суждение и умозаключение. Формальная логика определяет правила, которые обеспечивают истинный вывод. Как выводится умозаключение?

По этому примеру легко можно понять, что обозначает умозаключение, и какая его связь с суждением. Самое важное, чтобы суждения были истинными, в противном случае будет ложный вывод. Также немаловажное условие: связи между посылками обязаны быть правильно выстроены по логике, чтобы безошибочно и постепенно выстраивать путь дальше – от суждений к заключению.

Три типа умозаключений

Разделение на типы проводится после определения степени общности суждений:

Дедуктивное умозаключение строится от общего к частному. На дедукцию работают логические посылки любых союзов: условно-разделительное, разделительно-категорическое и категорическое умозаключение. Дедукцию изучают с категорического умозаключения – силлогизм (с греческого переводится «сосчитывание»). В этом случае свою работу начинает анализ рассуждений, складывающихся из понятий и суждений.

Примеры извлечения умозаключения

Умный человек может из минимума знаний иметь максимум информации и предугадать ситуацию со всеми вытекающими последствиями его действий. Отличный пример — Шерлок Холмс и доктор Ватсон. Силлогизмы состоят из двух и больше посылок и также делятся, с учетом характера составляющих суждений. Силлогизмы могут быть сложносокращенные и сокращенные, простые и сложные.

Непосредственные умозаключения

Как уже говорили, непосредственные умозаключения – это умозаключения, которые могут быть выведены из одной посылки. С помощью противопоставления, обращения, превращения создается логическое умозаключение. Суждение в связке изменяет качество посылки на противоположное, превращение – это изменение качества посылки с сохранением количества, а предикат или утверждение – на понятие, полностью противоречащее заключению.

В обращениях же местами изменяются предикат и субъект при абсолютном подчинении правилу распределения терминов суждения. Обращение могут быть с ограничением и простыми (чистыми).

Противопоставления – это непосредственные заключения, в котором субъект переходит в предикат, а на его место становится понятие, которое полностью противоречит исходному суждению. То есть, связка изменяется на противоположную. Противопоставление можно рассматривать как следствие после посылки и превращения.

Заключение по логике – это также разновидность непосредственных умозаключений, когда выводы основаны на логическом квадрате.

Категорическое умозаключение

Дедуктивный категорический силлогизм – это ситуация, в которой из двух истинных посылок следует умозаключение. Определения, которые находятся в составе силлогизма, обозначены терминами. Категорический простой силлогизм:

Виды силлогизма, отличающиеся в посылках по среднему термину (M), в категорическом силлогизме называют фигурами. Есть 4 фигуры, у каждой из них свои правила.

У любой фигуры существует несколько модусов (это различные силлогизмы по количественной и качественной характеристике посылок и умозаключений). В результате фигуры силлогизма имеют правильных 19 модусов, всем из них присвоено свое определение.

Условно-категорический силлогизм

Условное суждение может быть в одной посылке, а в другой посылке и умозаключении – категорические суждения. В этом случае модус бывает или отрицающий, или утверждающий. При утверждающем, когда другая посылка утверждает результат первой, заключение будет только верным. При отрицательном, когда отрицается истина условной посылки, заключение также получается только верным.

Разделительный силлогизм

Разделительным силлогизмом называется то заключение, которое состоит только из разделительных посылок, а умозаключение также получается разделительным суждением. То есть повышается количество альтернатив. Также существует разделительно-категорическое заключение, в котором первая посылка имеет разделительное суждение, а другая – простое категорическое. В этом случае два модуса: отрицающе-утверждающий и утверждающе-отрицательный.

Условно-разделительный силлогизм

Определение умозаключения в себя включает и условно-разделительный силлогизм, где одна посылка – это несколько условных суждения, а другая является разделительным суждением. Это также называется леммой. Основная цель леммы – это выбор из множества суждений.

Зачем необходимо понятие, суждение, умозаключение?

Сами по себе умозаключения не живут. Эксперименты не делаются вслепую. Все имеет смысл лишь в сочетании. Плюс теоретический анализ с синтезом, при котором с помощью обобщений, сравнений и сопоставлений можно сделать заключение. При этом сделать по аналогии заключение можно как о непосредственно предметном, так и о том, что нельзя «пощупать». Как непосредственно можно воспринимать такие процессы, как развитие жизни на Земле или образование звезд? В этом случае и требуется абстрактное мышление.

Понятие

Определение абстрактного мышления имеет три формы: умозаключения, суждения и понятия. Последнее отражает наиболее существенные, общие, решающие и необходимые свойства. В понятии находятся все признаки реальности, хоть в некоторых случаях реальность не имеет наглядности. Если появляется понятие, то разум не берет в признаки основную часть несущественных или индивидуальных случайностей, он все представления и восприятия обобщает из максимального количества однородных предметов. Понятия является результатом обобщения информации определенного опыта.

В научных экспериментах понятия играют основную роль. Процесс изучения какого-либо предмета длителен: от поверхностного и простого к глубокому и сложному. С учетом накопления знаний об отдельных особенностях и свойствах появляются и умозаключения об этом предмете.

Суждение

С углублением познаний появляются умозаключения о предметах объективного мира, и происходит совершенствование понятий. Это главная форма мышления. Суждения отображают реальные связи явлений и предметов, все закономерности развития и их внутреннее содержание. Любое положение и любой закон в реальном мире можно отобразить конкретным суждением. В логике этого процесса умозаключение играет особую роль.

Явление умозаключения

Свойственная для людей способность к умозаключениям – это особый мыслительный акт, при котором из суждений можно вывести новую предпосылку о предметах и событиях. Без данной способности нельзя было бы познавать мир. Продолжительное время невозможно было увидеть нашу планету со стороны, но и в этом случае человечество пришло к умозаключению, что наша планета круглая. Смогла помочь правильная связь истинных посылок: Земля во время затмений на Луну накладывает круглую тень; шарообразные предметы дают тень в виде круга; Земля имеет круглую форму. Заключение по аналогии!

Правильность заключений будет зависеть от двух факторов: посылки, на основе которых строятся умозаключения, обязаны соответствовать истине; связи посылок обязаны соотноситься с логикой, изучающей все формы и законы выстраивания посылок в умозаключении.

То есть умозаключение, суждение и понятие как основа абстрактного мышления дают возможность человечеству раскрывать самые существенные и самые важные стороны, связи окружающей и закономерной действительности, таким образом, познавать объективный мир.

Источник

СИЛЛОГИЗМ

Полезное

Смотреть что такое «СИЛЛОГИЗМ» в других словарях:

СИЛЛОГИЗМ — [гр. sillogismos] лог. умозаключение, состоящее из двух суждений (посылок), из которых следует третье суждение заключение, вывод (напр., всякое S есть M, а всякое M есть P, следовательно, всякое S есть P). Словарь иностранных слов. Комлев Н.Г.,… … Словарь иностранных слов русского языка

силлогизм — См. доказательство. Словарь русских синонимов и сходных по смыслу выражений. под. ред. Н. Абрамова, М.: Русские словари, 1999. силлогизм вывод, доказательство; рассуждение, умозаключение, энтимема, модус Словарь р … Словарь синонимов

Силлогизм — Силлогизм ♦ Syllogisme Тип дедуктивного умозаключения, сформулированный Аристотелем, объединяющий три термина, связанных попарно, каждый из которых упоминается дважды, в трех суждениях. Однако каноническим примером силлогизма служит… … Философский словарь Спонвиля

СИЛЛОГИЗМ — (греч. syllogismos) рассуждение, в котором две посылки, связывающие субъекты (подлежащие) и предикаты (сказуемые), объединены общим (средним) термином, обеспечивающим замыкание понятий (терминов) в заключении силлогизма. Напр.: Все металлы… … Большой Энциклопедический словарь

СИЛЛОГИЗМ — СИЛЛОГИЗМ, силлогизма, муж. (греч. syllogismos) (филос.). В формальной логике умозаключение, в котором из двух ранее установленных суждений, называемых посылками, получается третье суждение, называемое выводом. Толковый словарь Ушакова. Д.Н.… … Толковый словарь Ушакова

СИЛЛОГИЗМ — СИЛЛОГИЗМ, а, муж. В логике: умозаключение, в к ром из двух данных суждений (посылок) получается третье (вывод). | прил. силлогистический, ая, ое и силлогический, ая, ое. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

СИЛЛОГИЗМ — муж., греч. умствованье, рассужденье, из трех предложений: большой и малой посылки, и заключенья. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля

СИЛЛОГИЗМ — (от греч. syllogismos рассуждение, умозаключение) англ. syllogism; нем. Syllogismus. Умозаключение, состоящее из двух суждений (посылок), из к рых следует третье суждение (вывод). Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии

силлогизм — СИЛЛОГИЗМ, В широком смысле любое дедуктивное умозаключение, в узком смысле двухпосылочное умозаключение, состоящее из атрибутивных высказываний, в котором вывод об отношении между двумя терминами делается на основании отношения каждого… … Энциклопедия эпистемологии и философии науки

Источник

Урок 7. Силлогизмы

Этот урок будет посвящён многопосылочным умозаключениям. Так же как и в случае однопосылочных умозаключений, вся необходимая информация в скрытом виде будет присутствовать уже в посылках. Однако, поскольку посылок теперь будет много, то способы её извлечения становятся более сложными, а потому и добытая в заключении информация не будет казаться тривиальной. Кроме того, нужно отметить, что существует много разных видов многопосылочных умозаключений. Мы с вами сосредоточимся только на силлогизмах. Они отличаются тем, что и в посылках и в заключении имеют категорические атрибутивные высказывания и на основании наличия или отсутствия каких-то свойств у объектов позволяют сделать вывод о наличии или отсутствии у них других свойств.

Содержание:

Простой категорический силлогизм

Простой категорический силлогизм – это одно из наиболее простых и часто встречающихся умозаключений. Он состоит из двух посылок. В первой посылке говорится об отношении терминов А и В, во второй – об отношениях терминов В и С. На основании этого делается вывод об отношении терминов А и С. Такой вывод возможен потому, что обе посылки содержат общий термин В, который опосредует отношение между терминами А и С.

В данном случае, термин «рыбы» – это общий термин для двух посылок, и он помогает связать термины «акулы» и «существа, способные жить без воды». Общий термин для двух посылок принято называть средним термином. Субъект заключения (в нашем примере это «акулы») называют меньшим термином. Предикат заключения («существа, способные жить без воды») называют бóльшим термином. Соответственно, посылку, содержащую меньший термин, называют меньшей посылкой («Все акулы – это рыбы»), а посылку, содержащую больший термин, – бóльшей посылкой («Все рыбы не могут жить без воды»).

Естественно, в рассуждении посылки могут находиться в любой последовательности. Однако для удобства проверки правильности силлогизмов, большую посылку ставят всегда первой, а меньшую – второй. Тогда в зависимости от расположения терминов все простые категорические силлогизмы можно разделить на четыре вида. Эти виды называются фигурами.

Фигура – это форма простого категорического силлогизма, которая определяется расположением среднего термина.

Сверху расположена большая посылка, за ней следует меньшая посылка, под чертой находится заключение. Буквой S обозначен меньший термин, буквой P – больший термин, буквой М – средний термин.

Далее, фигуры могут наполняться разным содержанием, то есть на место посылок и заключений могут подставляться разные типы категорических атрибутивных высказываний. Например:

Эти различные сочетания высказываний в фигурах образуют так называемые модусы. Каждая фигура имеет 64 модуса, таким образом, на все четыре фигуры приходятся всего 256 модусов. Если подумать обо всём многообразии умозаключений, имеющих форму силлогизмов, то 256 модусов – это не так уж и много. Кроме того, далеко не все модусы образуют правильные умозаключения, то есть существуют такие модусы, которые при истинности посылок не гарантируют истинности умозаключения. Такие модусы называются неправильными. Правильными же называются те модусы, с помощью которых из истинных посылок мы всегда получаем истинное заключение. Всего существует 24 правильных модуса – по шесть на каждую фигуру. Это означает, что во всей классической силлогистике, которая исчерпывает львиную долю рассуждений, производимых людьми, существует всего 24 вида правильных умозаключений. Это очень маленькое число, поэтому правильные модусы не так уж и сложно запомнить.

Каждый из этих модусов ещё в Средние века получил особое мнемоническое наименование. Каждый тип категорического атрибутивного высказывания был обозначен с помощью всего одной буквы. Высказывания типа «Все S есть P» обозначили буквой «а», первой буквой в латинском слове «affirmo» («утверждаю»), и их запись превратилась в «SaP». Высказывания вида «Некоторые S есть P» записывались с помощью буквы «i», второй гласной в слове «affirmо», поэтому они выглядели как «SiP». Высказывания формы «Ни один S не есть P» обозначили буквой «е», первой гласной в латинском слове «nego» («отрицаю»), их стали записывать в виде «SeP». Как вы, наверное, уже догадались высказывания типа «Некоторые S не есть P» обозначили буквой «о», второй гласной в слове «nego», их формальная запись выглядела как «SoP». Поэтому модусы правильных силлогизмов традиционно обозначаются именно с помощью этих четырёх букв, которые для удобства запоминания представлены в виде слов. Таблица всех правильных модусов выглядит так:

К примеру, модус второй фигуры Cesare (eae) в развёрнутом виде будет выглядеть так:

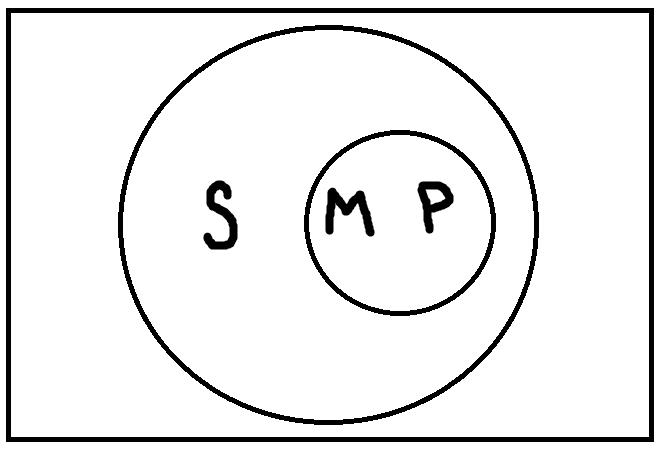
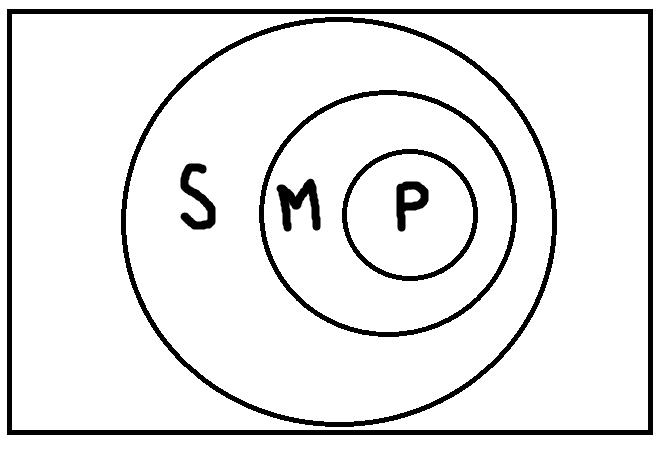
Хотя 24 модуса – это совсем не много и в таблице можно усмотреть некоторые регулярности (например, для всех фигур верны модусы eao и eio), запомнить её всё равно сложно. К счастью, это совсем и необязательно. Для проверки силлогизмов можно также пользоваться модельными схемами. Только в отличие от тех схем, которые мы строили раньше, на них уже должно присутствовать не два, а три термина: S, P, M.

Давайте возьмём модус четвёртой фигуры Bramantip (aai) и проверим его с помощью модельных схем.

Сначала нужно найти такие модельные схемы, при которых обе посылки будут одновременно истинными. Таких схем всего четыре:

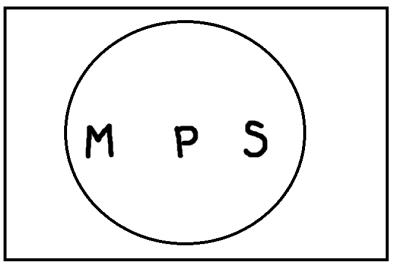
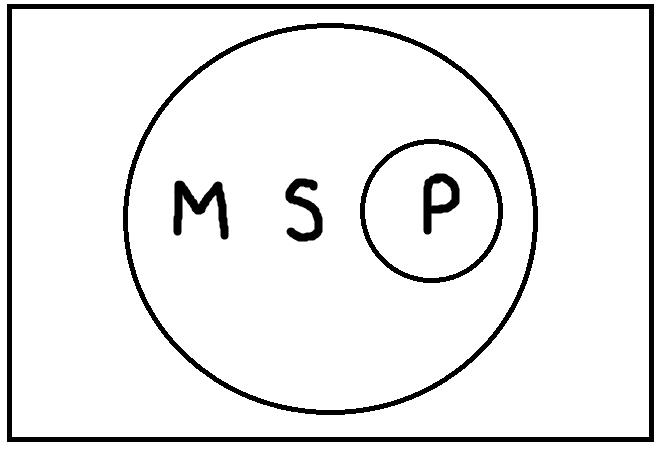
Теперь на каждой из этих схем мы должны проверить, верно ли будет высказывание «Некоторые S есть P», представляющее заключение. В результате проверки, мы обнаруживаем, что на каждой схеме это высказывание будет верным. Таким образом, умозаключение по модусу Bramantip (aai) четвёртой фигуры правильное. Если бы была хотя бы одна схема, на которой это высказывание было бы ложным, то умозаключение было бы неправильным.

Метод проверки силлогизмов с помощью модельных схем хорош, так как он позволяет представить отношения между терминами наглядно. Однако для некоторых посылок могут оказаться верными очень много схем сразу. В результате их построение и проверка будут представлять собой трудоёмкую и отнимающую много времени задачу. Таким образом, метод модельных схем не всегда удобен.

Поэтому логики разработали ещё один метод для определения, правильный силлогизм или нет. Этот метод называется синтаксическим и представляет собой два перечня правил (правила терминов и правила посылок), при соблюдении которых силлогизм будет верным.

Модус простого категорического силлогизма является правильным, если он удовлетворяет следующим условиям:

Правила терминов

Правила посылок понятны, а правила терминов требуют некоторых пояснений. Начнём с правила о трёх терминах. Хотя оно кажется очевидным, оно довольно часто нарушается вследствие так называемой подмены терминов. Посмотрите на следующий силлогизм:

Прежде всего, если вы помните фигуры и правильные модусы, вы сразу можете сказать, что этот силлогизм неправильный, так как он относится ко второй фигуре и имеет модус aaa, который не принадлежит к списку правильных модусов для этой фигуры. Но если вы их не помните, всё равно вы можете выявить его ложность, потому что здесь явно присутствует четыре термина, вместо трёх. Термин «золото» употребляется в двух совершенно различных смыслах: как химический элемент и как нечто, обладающее ценностью. Посмотрим на более сложный пример:

Кажется, что этот силлогизм соответствует модусу Barbara первой фигуры. Однако посылки истинны, а заключение ложно. Проблема в том, что в этом примере опять произошло учетверение терминов. Вроде бы этот силлогизм содержит три термина. Меньший термин – «”Отцы и дети” Ивана Тургенева». Больший термин – «книги, которые нельзя прочитать за целую жизнь». Средний термин – «книги из собрания Российской государственной библиотеки». Если же присмотреться внимательно, то станет ясно, что субъектом первой посылки является не термин «книги из собрания Российской государственной библиотеки», а термин «все книги из собрания Российской государственной библиотеки». В данном случае «все» – это не квантор общности, а часть субъекта, так как это слово употребляется не в разделительном смысле (каждый в отдельности), а в собирательном (все вместе). Если бы мы заменили слово «все» на слова «каждый в отдельности», то первая посылка попросту стала бы ложной: «Каждую в отдельности книгу из собрания Российской государственной библиотеки нельзя прочитать за целую жизнь». Таким образом, мы получаем четыре термина вместо трёх, а потому это умозаключение ложно.

Теперь перейдём к правилам о распределённости терминов. Для начала объясним, что это за характеристика. Термин называют распределённым, если в высказывании речь идёт обо всех объектах, входящих в его объём. Соответственно, термин не распределён, если в высказывании речь идёт не обо всех объектах, составляющих его объём. Грубо говоря, термин распределён, если мы говорим обо всех предметах, и не распределён, если мы говорим только о некоторых предметах, о части объёма термина.

Давайте возьмём типы высказываний и посмотрим, какие термины в них распределены, а какие нет. Распределённый термин отмечается знаком «+», нераспределённый – знаком «–».

Как видно, субъект всегда распределён в общих и единичных высказываниях, но не распределён в частных. Предикат всегда распределён в отрицательных высказываниях, но не распределён в утвердительных. Если теперь перенести это на наши правила для терминов, то получается, что средний термин хотя бы в одной из посылок должен быть взят во всём своём объёме.

Хотя и высказывания над чертой и высказывание под чертой истинны, умозаключение как таковое здесь отсутствует. Здесь нет логического перехода от посылок к заключению. И это можно легко выявить, так как средний термин «птицы» ни разу не берётся во всём своём объёме.

Что касается третьего правила терминов, если в посылках речь идёт только о части объектов из объёма терминов, то в заключении мы не можем ничего утверждать обо всех объектах объёма терминов. Мы не можем перейти от части к целому. Кстати, обратный переход возможен: если мы говорим обо всех элементах объёма терминов, то мы можем сделать заключение о части из них.

Задачи Эйнштейна

Эта игра является нашей версией всемирно известной «загадки Эйнштейна», в которой 5 иностранцев живут на 5 улицах, едят 5 видов еды и т.д. Подробнее про эту задачу написано здесь. В подобных заданиях вам нужно сделать правильное умозаключение на основе имеющихся посылок, которых, на первый взгляд, для этого недостаточно.

Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.

Энтимемы

Во время реальных дискуссий и споров мы довольно часто опускаем те или иные части рассуждения. Это приводит к возникновению энтимем. Энтимема – это сокращённая форма умозаключения, в которой пропущены посылки или заключение. Важно не путать энтимемы с однопосылочными умозаключениями. Энтимема – это именно многопосылочное умозаключение, просто его части в силу тех или иных причин опущены. Иногда такие пропуски оправданы, так как оба собеседника хорошо разбираются в проблеме, и им нет нужды проговаривать все шаги. Между тем, недобросовестные собеседники могут специально пользоваться энтимемами, чтобы затемнить и запутать своё рассуждение и скрыть свои истинные аргументы или выводы. Поэтому необходимо уметь отличать корректные энтимемы от некорректных. Энтимема называется корректной, если она может быть восстановлена в виде правильного модуса категорического силлогизма, и если все пропущенные посылки оказываются истинными.

Поговорим о том, как восстановить энтимему до полного силлогизма. В первую очередь нужно понять, что именно пропущено. Для этого нужно обратить внимание на слова-маркеры, обозначающие причинно-следственные связи: «таким образом», «следовательно», «так как», «потому что», «в результате» и т.д. К примеру, возьмём рассуждение: «Золото – это драгоценный металл, потому что оно практически не окисляется на воздухе». Здесь заключением является высказывание «Золото – это драгоценный металл». Одна из посылок: «Золото практически не окисляется на воздухе». Ещё одна посылка пропущена. Нужно сказать, что чаще всего пропускают именно одну из посылок. Довольно странно, если в рассуждении отсутствует самое важное – вывод.

Итак, мы установили, что именно пропущено. В нашем примере – это посылка. Большая это посылка или меньшая? Как вы помните, меньшая посылка содержит субъект заключения («золото»), а большая – предикат заключения («драгоценный металл»). Посылка, содержащая субъект заключения нам уже известна: «Золото практически не окисляется на воздухе». Значит, нам известна меньшая посылка, и не известна большая. Кроме того, благодаря известной посылке, мы можем установить и средний термин: «металлы, которые практически не окисляются на воздухе», – тот термин, который не содержится в заключении.

Теперь располагаем известную нам информацию в форме силлогизма:

В большей посылке должны находиться предикат заключения и средний термин: «драгоценные металлы» (P) и «металлы, которые окисляются на воздухе» (M). Здесь возможны два варианта:

Значит, возможен силлогизм либо второй фигуры, либо первой фигуры. Теперь смотрим на нашу табличку с правильными модусами силлогизмов. Во второй фигуре вообще нет правильных модусов, где в заключении стояло бы высказывание типа а. В первой фигуре есть только один такой модус – Barbara. Достраиваем наш силлогизм:

Теперь проверяем, истинна ли наша восстановленная посылка. В нашем случае она истинна, поэтому энтимема была правильной.

Сориты

Термином «сориты» пользовался Льюис Кэррол для обозначения сложных силлогизмов, которые имеют более чем две посылки. По большому счёту, сорит представляет собой гибрид силлогизма и энтимемы. Он устроен следующим образом: дано множество посылок, из каждой пары посылок делаются промежуточные выводы, которые обычно опускаются, к промежуточным выводам присоединяются новые посылки, из них делаются новые промежуточные выводы, к которым опять присоединяются новые посылки и так далее, пока мы не переберём все имеющиеся посылки и не дойдём до окончательного заключения. В принципе подобным образом люди и рассуждают в повседневной жизни. Поэтому очень важно уметь решать сориты и оценивать, правильны они или нет.

Мы приведём пример сорита из книги Льюиса Кэррола «История с узелками»:

1. Все полисмены из нашей округи ужинают у нашей кухарки.
2. Человек с длинными волосами не может не быть поэтом.
3. Амос Джадд никогда не сидел в тюрьме.
4. Все кузены нашей кухарки любят холодную баранину.
5. В этой округе нет других поэтов, кроме полисменов.
6. С нашей кухаркой не ужинает никто, кроме её кузенов.
7. Все люди с короткими волосами сидели в тюрьме.

8. Амос Джадд любит холодную баранину.

Над чертой находятся посылки, под чертой – заключение.

Как же нужно решать и проверять сориты? Дадим пошаговую инструкцию. Во-первых, необходимо привести все посылки в более или менее стандартную форму:

1. Все полисмены из нашей округи ужинают у нашей кухарки.
2. Все люди с длинными волосами являются поэтами.
3. Амос Джадд не сидел в тюрьме.
4. Все кузены нашей кухарки любят холодную баранину.
5. Все поэты из нашего округа являются полисменами.
6. Все люди, ужинающие с нашей кухаркой, приходятся ей кузенами.
7. Все люди с короткими волосами сидели в тюрьме.

Теперь нужно взять две исходные посылки. По большому счёту, неважно, с каких именно посылок вы начнёте. Главное, чтобы ваши исходные посылки вместе содержали всего три термина. Это означает, что мы не можем взять посылки «Амос Джадд не сидел в тюрьме» и «Все кузены нашей кухарки любят холодную баранину». В них входят четыре разных термина, а потому мы не можем сделать из них никакого заключения. Я в качестве исходных возьму посылки 7 и 3 и сделаю из них вывод по правилам для простых категорических силлогизмов.

Этот силлогизм соответствует модусу Camestres (aee) второй фигуры. Теперь для удобства я переформулирую наш промежуточный вывод следующим образом: «Амос Джадд является человеком с длинными волосами». Этот промежуточный вывод я соединяю с посылкой номер 2:

Этот силлогизм соответствует модусу Barbara (aaa) первой фигуры. Теперь я присоединяю этот промежуточный вывод к посылке номер 5:

Этот силлогизм опять же соответствует модусу Barbara (aaa) первой фигуры. Присоединяем промежуточный вывод к посылке номер 1:

Это силлогизм, как вы уже, наверное, заметили, тоже представляет собой модус Barbara (aaa) первой фигуры. Присоединяем этот вывод к посылке номер 6:

Опять Barbara, которая является одним из самых распространённых модусов. Присоединяем к нашему последнему промежуточному выводу последнюю посылку номер 4:

Итак, с помощью всё того же модуса Barbara мы получили наше заключение: «Амос Джадд любит холодную баранину». Таким образом, сориты решаются и проверяются с помощью пошагового разделения на простые категорические силлогизмы. В нашем примере сорит оказался правильным, но возможны и обратные ситуации. Существует два условия корректности соритов. Во-первых, каждый сорит должен разбиваться на последовательность правильных модусов силлогизмов. Во-вторых, заключение, которое вы получаете, когда все посылки исчерпаны, должно совпасть с заключением сорита. Это условие действует в тех случаях, когда вы имеете дело с чужим рассуждением, в котором уже присутствует какое-то заключение.

Итак, мы рассмотрели различные многопосылочные умозаключения на примере простых категорических силлогизмов, энтимем и соритов. По большому счёту, если вы знаете, как иметь с ними дело, то вы вооружены для любых дискуссий с любыми противниками. Единственное, что может на данный момент вызывать некоторое недовольство, это необходимость тратить много времени на проверку правильности умозаключений. Не стоит расстраиваться по этому поводу: лучше выглядеть тугодумом, который рассуждает правильно, чем блестящим демагогом, который не замечает своих и чужих ошибок. Тем более, с накоплением опыта внимательного отношения к умозаключениям у вас появится чутьё, автоматический навык, позволяющий быстро отделять корректные рассуждения от некорректных. Поэтому упражнений к этому уроку будет много, чтобы у вас была возможность набить руку.

Упражнения

Упражнения 1, 2 и 3 взяты из книги Льюиса Кэррола «История с узелками», М.: Мир, 1973.

Упражнение 1

Сделайте заключения из следующих посылок по правилам для простого категорического силлогизма. Помните, что простой категорический силлогизм должен содержать только три термина. Не забывайте приводить высказывания к стандартному виду.

Упражнение 2

Проверьте, правильны ли следующие рассуждения. Попробуйте разные способы проверки. Не забывайте ставить большую посылку на первую строку.

Упражнение 3

Найдите заключения следующих соритов.

Упражнение 4

Проверьте правильность следующих энтимем.

Проверьте свои знания

Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.

Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.

Источник