Что такое систематическая и случайная погрешности измерений
Систематические и случайные погрешности.
Систематические погрешности – это погрешности, вызываемые факторами, действующими постоянно (т.е. систематически). Их можно обнаружить и измерить с помощью более точных приборов. Прибор, дающий систематическую погрешность, всегда завышает или всегда занижает свои показания, то есть во всех измерениях значения абсолютной погрешности – это числа одного знака. Но по модулю она может быть от случая к случаю различной.
Причины появления систематических погрешностей могут быть тривиальными (например, разрядилась батарейка), а могут быть и более коварными (непостоянство диаметра капилляра в термометре; несовершенство методики косвенных измерений). Количество возможных причин может исчисляться десятками. Единой методики выявления причин появления систематических погрешностей не существует.
Вопрос для быстро соображающих: какие неожиданности грозят автомобилисту, если он контролирует расход топлива по показаниям уровнемера, а бензобак сужается книзу? Какую погрешность имеет уровнемер?
Если систематическая погрешность обнаружена и оценена количественно, то возможны следующие варианты действий:
— устранение ее причины;
— коррекция показаний состоявшихся и будущих измерений на величину систематической погрешности;
— пренебрежение систематической погрешностью, если она достаточно мала.
Случайные погрешности имеют следующие свойства:
1. Одинаковые по модулю положительные и отрицательные погрешности равновероятны.
2. Меньшие по модулю погрешности встречаются чаще, чем большие.
3. С увеличением числа измерений одной и той же величины, среднее арифметическое значение случайных погрешностей, посчитанное с учетом их знаков, стремится к нулю. Это означает, что с ростом количества измерений среднеарифметическое значениерезультатов измеренийстремится к истинному значению измеряемой величины.
Случайные и систематические погрешности могут спокойно сосуществовать друг с другом.
Нормальный закон распределения в экспериментальных
Исследованиях.
Случайные величины, обладающие свойствами 1 – 3 предыдущего раздела, можно сказать, предрасположены к тому, чтобы иметь распределение вероятности, известное как распределение Гаусса (нормальный закон распределения). По нормальному закону распределено очень многое в самых разнообразных областях знаний.
Универсальность нормального закона сумел обосновать А.М. Ляпунов. Согласно его теореме, если случайная величина Х представляет собой сумму очень большого числа взаимно независимых случайных величин х1, х2, …, хn, влияние каждой из которых на всю сумму ничтожно мало՜, то независимо от того, каким законам подчиняются слагаемые х1, х2, …, хn, сама величина Х будет иметь распределение вероятностей, близкое к нормальному, и тем точнее, чем больше число слагаемых n.
В ходе любого медико-биологического эксперимента, накопив выборку результатов измерений некоего параметра, имеет смысл проверить ее на соответствие нормальному закону распределения, применив подобающий случаю статистический критерий (Шапиро-Уилка, Пирсона).
При этом, любой результат проверки по-своему интересен. Если гипотеза о нормальном распределении принимается, вы получаете возможность применить к этому параметру все свои познания о свойствах нормально распределенных величин. Если же гипотеза не принимается, вы приходите к выводу, что среди множества факторов, влияющих на исследуемый параметр, есть доминирующие по влиянию, и их неплохо бы выявить; и это уже – призыв к действиям в нужном направлении.
Что касается применимости нормального закона к погрешностям измерений, то если систематические погрешности устранены (или вычтены из результатов измерений), то по опыту исследований погрешностей в измерительных системах, оставшиеся случайные погрешности распределены по нормальному закону или очень близки к нему.
Контрольные вопросы по теме «Вводное занятие».
1. Измерения. Основные единицы системы СИ.
2. Производные единицы системы СИ для частоты, силы, давления,
3. Производные единицы системы СИ для электрических и магнитных
величин: заряд, потенциал, сопротивление, электроемкость, магнитная
индукция, поток магнитной индукции, индуктивность.
4. Некоторые внесистемные единицы: миллиметр ртутного столба, калория,
электронвольт, лошадиная сила.
5. Дробные и кратные единицы.
6. Прямые и косвенные измерения. Примеры.
7. Абсолютная и относительная погрешность измерений. Методы оценки
8. Доверительный интервал. Доверительная вероятность. Уровень
9. Систематические погрешности, их происхождение, свойства, способы
выявления и уменьшения.
10. Случайные погрешности, их происхождение, свойства, способы
выявления и уменьшения.
11. Нормальный закон распределения: причины его универсальности;
применение в эксперименте.
БИОАКУСТИКА. ЗВУК.
В этой главе рассматриваются вопросы физики слуха:
— характеристики колебаний и волновых процессов;
— получение, распространение и особенности восприятия звука в привычном смысле этого слова, то есть звуковых волн слышимого диапазона частот
— строение уха, его функционирование, вопросы контроля качества слуха.
Заключительный раздел – методические указания по выполнению лабораторной работы «Определение порогов слышимости с помощью аудиометра».
Систематические и случайные погрешности. Систематической погрешностью называется погрешность, остающаяся постоянной или закономерно изменяющейся во времени при повторных измерениях одной и той же



Систематической погрешностью называется погрешность, остающаяся постоянной или закономерно изменяющейся во времени при повторных измерениях одной и той же величины.
Примером систематической погрешности, закономерно изменяющейся во времени, может служить смещение настройки прибора во времени.
Случайной погрешностью измерения называется погрешность, которая при многократном измерении одного и того же значения не остаётся постоянной. Например, при измерении валика одним и тем же прибором в одном и том же сечении получаются различные значения измеренной величины.
Систематические и случайные погрешности чаще всего появляются одновременно.
Для выявления систематической погрешности производят многократные измерения образцовой меры и по полученным результатам определяют среднее значение размера. Отклонение среднего значения от размера образцовой меры характеризует систематическую погрешность, которую называют «средней арифметической погрешностью», или «средним арифметическим отклонением».
Систематическая погрешность всегда имеет знак отклонения, т.е. «+» или «-«. Систематическая погрешность может быть исключена введением поправки.
Прогрессивные и периодические систематические погрешности в противоположность постоянным можно обнаружить при многократных измерениях.
Обработка данных и оценка параметров случайных погрешностей производится методами математической статистики.
При расчёте предельной погрешности измерения определяют числовое значение погрешности измерения от всех составляющих и производят суммирование:
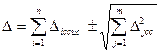
где знаки «+» или «-» ставятся из условия, чтобы систематические и случайные погрешности суммировались по модулю.
Если в случайной погрешности известно среднее квадратическое отклонение, то
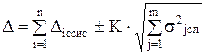
Если результаты измерений зависят от большого числа разнообразных факторов, то
Каждый параметр может иметь отклонение Dxi (погрешность) от предписанного значения xi. Поскольку погрешность Dxi мала по сравнению с величиной xi, суммарная погрешность Dy функции y можно вычислять по формуле 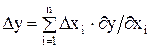
Формула (5) справедлива лишь для систематических погрешностей Dxi.
Для случайных погрешностей (когда отдельные составляющие не всегда принимают предельные значения) используются теоремы теории вероятностей о дисперсии, то есть
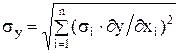
Суммарная погрешность при наличии только случайных составляющих dxi погрешностей
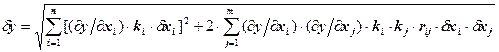
При наличии и систематических и случайных составляющих погрешностей вычисляют доверительные границы суммарной погрешности:
Что такое систематическая и случайная погрешности измерений
Всероссийский научно-исследовательский институт
оптико-физических измерений




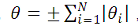
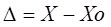 (1.2), где X — результат измерения; Х0 — истинное значение этой величины.
(1.2), где X — результат измерения; Х0 — истинное значение этой величины.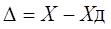 (1.3), где Хд — действительное значение этой измеряемой величины, которое с погрешностью ее определения принимают за истинное значение.
(1.3), где Хд — действительное значение этой измеряемой величины, которое с погрешностью ее определения принимают за истинное значение.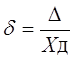 (1.4)
(1.4)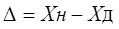 (1.5), где Xн – номинальное значение меры; Хд – действительное значение меры
(1.5), где Xн – номинальное значение меры; Хд – действительное значение меры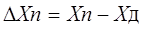 (1.6), где Xп – показания прибора; Хд – действительное значение измеряемой величины.
(1.6), где Xп – показания прибора; Хд – действительное значение измеряемой величины.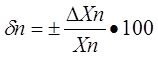 (1.7)
(1.7)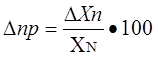 (1.8)
(1.8)