Что такое скалярное перемещение
Скалярные и векторные величины в физике и математике
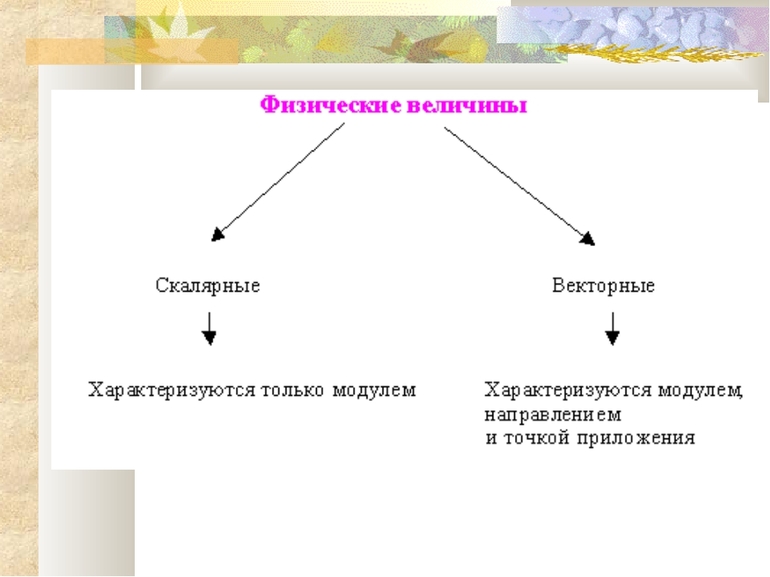
Особенности скалярных величин
Скалярные величины характеризуются только одним параметром — числовым значением. Они разделяются на 2 вида:
В физике в список скалярных величин входят:
Если скаляры выражают одно единственное свойство физического тела, то они называются однородными. Величины, описывающие несколько свойств объекта, именуются разнородными. Однородные скаляры сравнимы: они либо равны, либо одна из них больше или меньше другой. Но скалярные величины разного рода не могут сравниваться друг с другом.
Определение положительного скаляра и его измерения
Понятие положительной скалярной величины и ее измерения позволяет сравнивать между собой однородные скаляры. Положительная скалярная величина способна принимать значения строго выше 0. Она обозначается знаком «+». Если величина может принимать значения меньше 0, то она называется отрицательной и обозначается символом «-«. Большинство скаляров могут быть только положительными. Для их расчета используют единицы измерения — фиксированного размера объекта.
Чтобы получить скалярную величину, достаточно умножить ее числовое значение на ее единицу измерения. Для структуризации и стандартизации вычислений физических параметров тела была разработана Международная система СИ. Она устанавливает единицы измерения для каждой величины. Во время проведения расчетов скалярных величин применяют алгебраические действия — сложение, вычитание, деление и умножение (отдельный подвид — возведение в степень).
Особенности векторных величин
Их определение: «В физике векторными величинами называются свойства материи, характеризующиеся несколькими параметрами: модулем и направлением». Модулем вектора будет являться числовое значение величины, никогда не принимающее отрицательных значений. Он обозначается символом «||». Для обозначения направления используется стрелка, располагающаяся над символом вектора.
В физике и математике примерами векторных величин являются:
На графиках функции векторные величины изображаются в виде прямой линии, имеющей направление и свои собственные координаты в заданном масштабе.
Свойства векторов
Вектор — математический элемент, представляющий собой прямой отрезок с направлением. Он обозначается либо 2 заглавными латинскими буквами, либо одной прописной. Длиной вектора является его модуль. Если длина вектора равняется 0, то он называется нулевым. Вектор, имеющий длину 1 см, именуется единичным. Длина ненулевого вектора выражается в виде расстояния между началом и концом направленного отрезка. Проекцией вектора на ось является строго положительный отрезок, сонаправленный с исходной осью. Свойства проекции:
Коллинеарные векторы — отрезки, располагающиеся либо на одной прямой, либо на параллельных прямых. Нулевой вектор коллинеарен всегда. Если коллинеарные векторы направлены в одну сторону, то они называются сонаправленными. Если отрезки направлены в диаметрально противоположные стороны, то они называются противоположно направленными. Коллинеарные векторы являются равными, если они одинаковы по модулю и направлению.
Построение отрезков с направлением на плоскости осуществляется при помощи его координат для осей абсцисса и ордината. Для изображения направленного отрезка необходимо построить точки, координаты которых соответствуют началу и концу вектора, и соединить их.
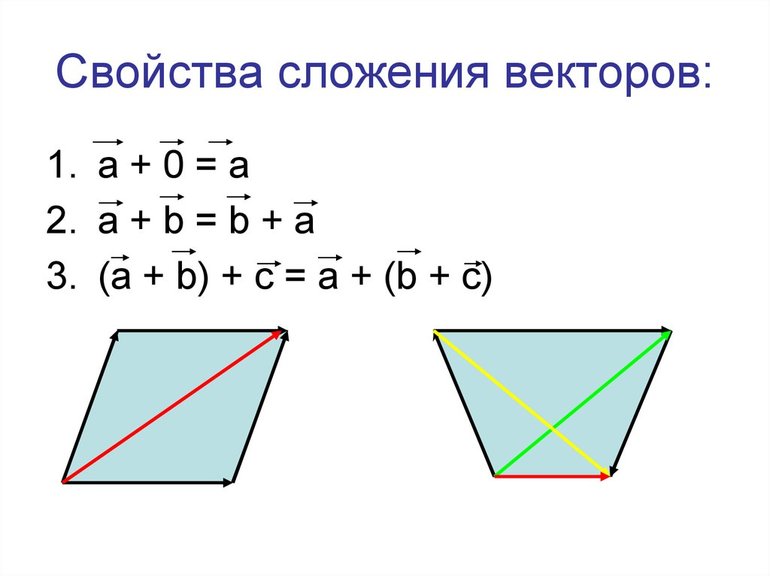
С векторами также можно производить операции сложения, деления, вычитания и умножения. Чтобы сложить два вектора, необходимо от произвольной точки на плоскости отложить первый направленный отрезок и от него отложить второй вектор. Отрезок, соединяющий начало первого вектора и конец второго, будет считаться их суммой. Этот способ сложения именуется методом треугольника.
Вторым способом нахождения суммы векторов является метод параллелограмма. От произвольной точки откладываются оба направленных отрезка. Полученный рисунок нужно достроить до параллелограмма. Диагональ фигуры будет являться суммой векторов.
Для осуществления вычитания необходимо отложить от произвольной точки первый вектор. От полученного отрезка откладывается следующий вектор. Второй отрезок нужно направить в противоположную сторону. Линия, соединяющая отрезки, будет являться разностью векторов.
С векторами также можно проводить операцию умножения. Произведение длин направленных отрезков на косинус угла между ними называется скалярным. В результате вычислений получается число — скаляр. Скалярное произведение равно 0 в случае, когда отрезки пересекаются под углом 90°. Зная скалярное произведение, человек сможет найти косинус угла между построенными векторами.
Полученные в результате выполнения алгебраических операций выражения применяются для исследования перемещения тел вокруг оси вращения и изучения элементов высшей математики. Также направленные отрезки нашли широкое применение в геометрии и астрономии.
Кинематика
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Прямолинейное равномерное движение
Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.
Например, если у вас ограничение скорости на дороге 60 км/ч и у вас нет никаких препятствий на пути, то вы скорее всего будете двигаться прямолинейно равномерно.
Мы можем охарактеризовать это движение следующими величинами.
Скалярные величины (определяются только значением)
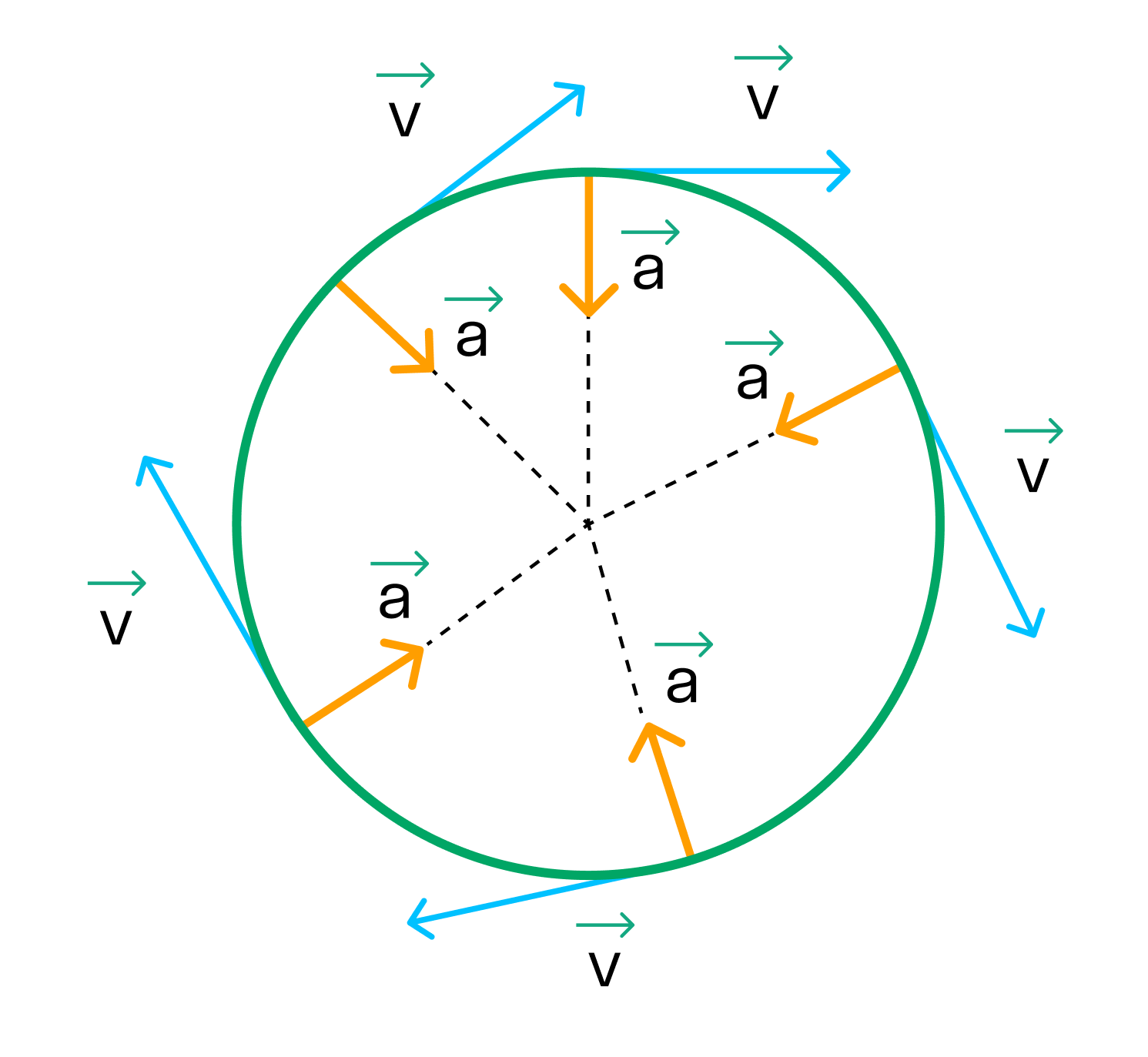
Векторные величины (определяются значением и направлением)
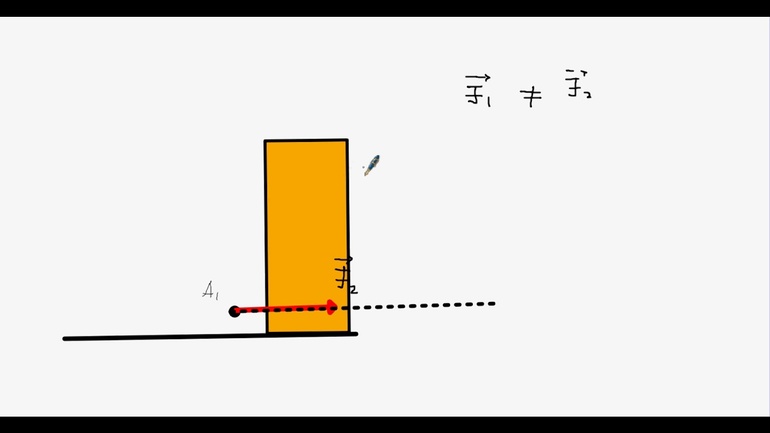
Проецирование векторов
Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.
Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.
Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю.
Скорость может определяться по вектору перемещения и пути, только это будут две разные характеристики. Скорость — это векторная физическая величина, характеризующая быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.
Скорость
→ →
V = S/t
Средняя путевая скорость
V ср.путевая = S/t
V ср.путевая — средняя путевая скорость [м/с]
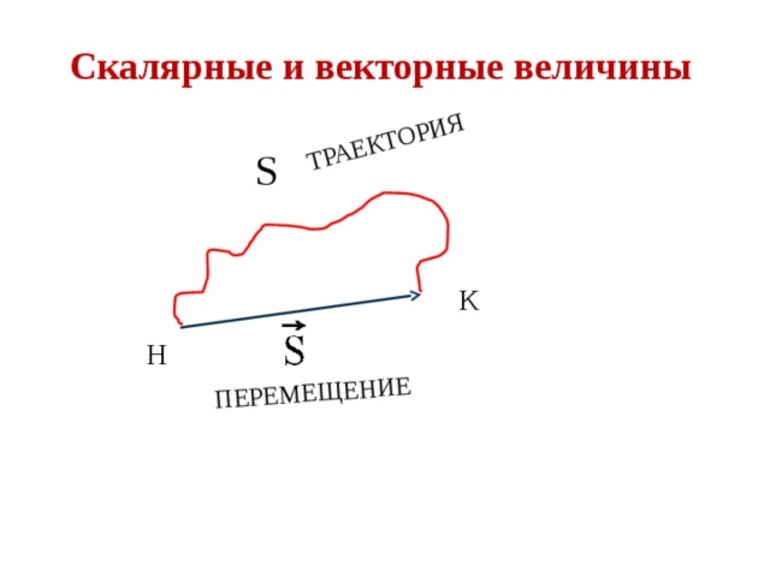
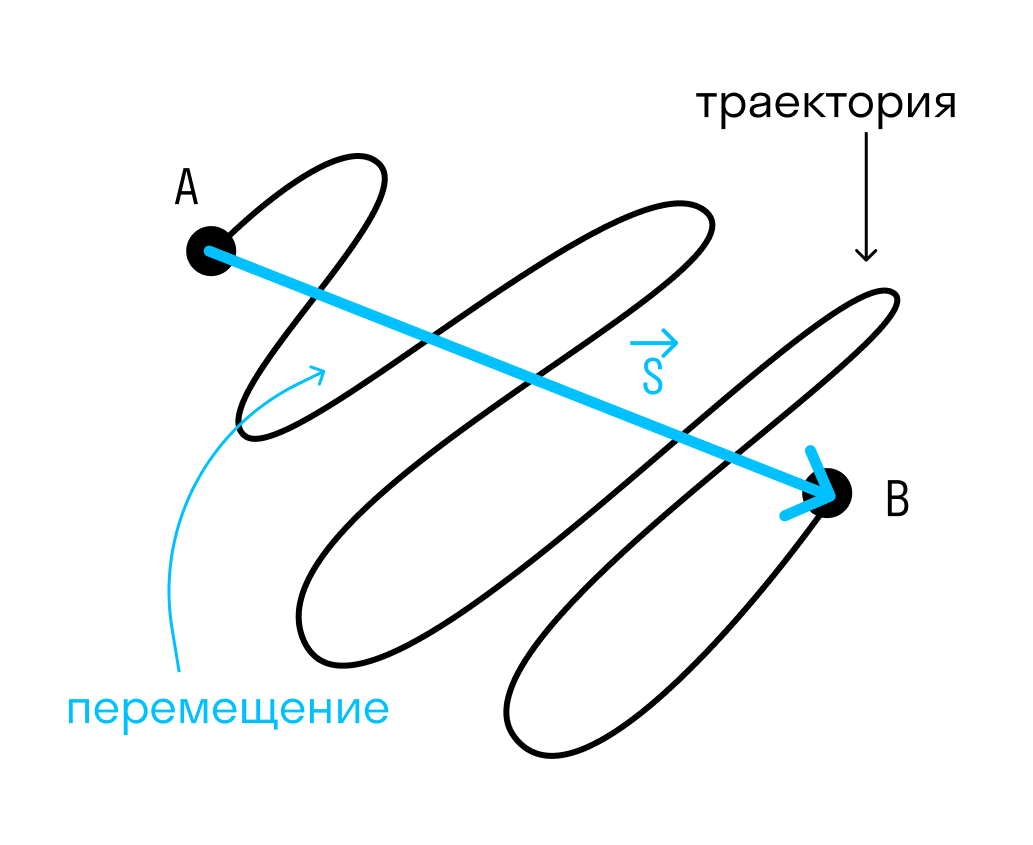
В чем разница между перемещением и путем?
Перемещение — это вектор, проведенный из начальной точки в конечную, а путь — это длина траектории.
Задача
Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.
Решение:
Возьмем формулу средней путевой скорости
V ср.путевая = 210/2,5 = 84 км/ч
Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч
Уравнение движения
Основной задачей механики является определение положения тела в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).
Уравнение движения
x(t) = x0 + vxt
x(t) — искомая координата [м]
x0 — начальная координата [м]
vx — скорость тела в данный момент времени [м/с]
t — момент времени [с]
Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v