Что такое скалярное уравнение

Большая Энциклопедия Нефти и Газа

Скалярное уравнение

Скалярное уравнение д ( А) 0 имеет степень mn, и, как показано в предыдущем пункте настоящего параграфа, его решения распадаются на классы подобных между собой матриц. [1]

Скалярное уравнение имеет степень тп и, как показано в предыдущем пункте настоящего параграфа, его решения распадаются на классы подобных между собой матриц. [2]

Скалярные уравнения равновесия (5.35) отнесены к ортам деформированной осевой линии стержня. [5]

Скалярные уравнения равновесия (5.81) отнесены к ортам деформированной осевой линии стержня. [6]

Скалярные уравнения равновесия (5.35) отнесены к ортам деформированной осевой линии стержня. [7]

Скалярные уравнения равновесия (5.81) отнесены к ортам деформированной осевой линии стержня. [8]

Векторные и скалярные уравнения механики действительно обладают этим свойством. Однако это не обязательно для любого уравнения; вообще говоря, скаляры и векторы при инверсии могут изменяться. По отношению к инверсии скаляры делятся на истинные скаляры ( или просто скаляры) и псе вдо скаляры. [10]

Сколько независимых скалярных уравнений равновесия можно получить в том случае, когда все силы, приложенные к твердому телу, вместе с точками их приложения принадлежат некоторой плоскости. Какие варианты составления уравнений равновесия при этом возможны. [11]

Вещественными скалярными уравнениями не может быть описано все та многообразие волн, которое наблюдается экспериментально / Большинство физических и биологических задач приводит не к скалярным уравнениям, а к системам уравнений. [12]

Тогда скалярное уравнение (13.1) виброкорректно в целом. [13]

Одно скалярное уравнение (1.3) и одно векторное (1.4) дают всего четыре скалярных уравнения. Для идеальной среды беэ вязкости и теплопроводности энтропия во всем пространстве, занятом непрерывно движущейся жидкостью, постоянна ( изэнтропическое движение), и внутренняя энергия жидкости изменяется только в результате адиабатического сжатия. [14]

Это скалярное уравнение описывает скорость изменения кинетической энергии на единицу массы ( ш2 / 2) для элемента жидкости, перемещающегося вниз по потоку. [15]

Источник

Скалярное произведение векторов: свойства, примеры вычисления, физический смысл

Скалярное произведение векторов называют число, равное произведению дин этих векторов на косинус угла между ними.

При умножении вектора самого на себя, получим квадрат его дины:

Скалярное умножение вектора самого на себя называют скалярным квадратом.

Вычисляется по формуле:

Сформулируем определение произведения для двух векторов:

Скалярное произведение двух векторов a → на b → называют произведение длины вектора a → на проекцию b → на направление a → или произведение длины b → на проекцию a → соответственно.

Скалярное произведение в координатах

Вычисление скалярного произведения можно производить через координаты векторов в заданной плоскости или в пространстве.

для трехмерного пространства применимо выражение:

Фактически это является третьим определением скалярного произведения.

Следует отложить векторы

– соответственно для векторов трехмерного пространства.

Скалярное произведение и его свойства

Свойства объяснимы благодаря определению скалярного произведения на плоскости и свойствам при сложении и умножении действительных чисел.

Дистрибутивность справедлива для любых чисел:

Скалярное произведение с примерами и решениями

Любая задача такого плана решается с применением свойств и формул, касающихся скалярного произведения:

Рассмотрим некоторые примеры решения.

Длина a → равна 3, длина b → равна 7. Найти скалярное произведение, если угол имеет 60 градусов.

По условию имеем все данные, поэтому вычисляем по формуле:

В данном примере рассматривается формула вычисления по координатам, так как они заданы в условии задачи:

Для начала вычисляются координаты векторов, так как по условию даны координаты точек:

Подставив в формулу с использованием координат, получим:

Выносим коэффициент за знак произведения и получим:

По свойству коммутативности преобразуем:

Теперь применим формулу для скалярного произведения с заданным по условию углом:

Если имеется числовая проекция.

Подставив в формулу, получим выражение:

Задачи при известном скалярном произведении, где необходимо отыскать длину вектора или числовую проекцию.

Из формулы видно, что необходимо найти сумму произведений координат:

Физический смысл скалярного произведения

Механика рассматривает приложение скалярного произведения.

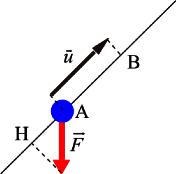
При работе А с постоянной силой F → перемещаемое тело из точки M в N можно найти произведение длин векторов F → и M N → с косинусом угла между ними, значит работа равна произведению векторов силы и перемещения:

Источник

Скалярное произведение

Поскольку существует два основных способа определения векторов, либо чисто алгебраический подход (см. Статью « Векторное пространство »), либо геометрический подход с использованием бипоинт (или пар точек, см. « Вектор »), есть также два способа представления скалярного произведения: алгебраическим способом (тема статьи « Доильбертово пространство ») и геометрическим способом с использованием бипоинтов.

Исторически скалярное произведение геометрически представляло себя в традиционном евклидовом пространстве до того, как это понятие распространилось на любое реальное векторное пространство.

Резюме

Обзор приложений скалярного произведения

Наконец, статья « Евклидова геометрия » предлагает синтез истории, последствий и приложений скалярного произведения в конечномерном измерении.

Фрагменты истории

Оценка скалярного произведения с помощью точки или креста была предложена Джозией Уиллардом Гиббсом в 1880-х годах.

Однако выражение « скалярный продукт» впервые появляется в научной публикации в книге Уильяма Кингдона Клиффорда, датированной 1878 годом. Тем не менее, это авторство подвергается сомнению М. Дж. Кроу, для которого работа Клиффорда представляет собой переход от алгебры кватернионов, описанной Гамильтоном, к формализации векторных пространств.

Определения и первые свойства

Если один из векторов равен нулю, то скалярное произведение равно нулю.

Во всех случаях мы обозначаем это скалярное произведение: О В → ⋅ О B → <\ displaystyle <\ overrightarrow > \ cdot <\ overrightarrow >>

Если ни один из векторов не равен нулю, это определение принимает следующий вид:

О В → ⋅ О B → знак равно О В × О B × потому что ⁡ ( В О B ^ ) <\ displaystyle <\ overrightarrow > \ cdot <\ overrightarrow > = OA \ times OB \ times \ cos (<\ widehat >)>

В случае, когда два вектора равны, используются следующие обозначения:

О В → ⋅ О В → знак равно О В → 2 знак равно О В 2 <\ displaystyle <\ overrightarrow > \ cdot <\ overrightarrow > = <\ overrightarrow > ^ <2>= OA ^ <2>>

‖ В B → ‖ знак равно В B → ⋅ В B → <\ displaystyle \ left \ | <\ overrightarrow > \ right \ | = <\ sqrt [<>] <<\ overrightarrow > \ cdot <\ overrightarrow >>>> .

Очевидное неравенство проверяется таким определенным скалярным произведением:

Равенство возникает тогда и только тогда, когда три точки выровнены.

Это увеличение происходит из-за того, что функция косинуса принимает значения в интервале [–1, 1]. Чтобы равенство имело место, необходимо и достаточно, чтобы косинус имел значение либо 1, либо –1, то есть угол равен нулю или плоский, что означает, что три точки выровнены. Этому неравенству посвящена статья « Неравенство Коши-Шварца », которая также предполагает алгебраическую формализацию, отличную от выбранной здесь.

Геометрические свойства

Прогнозируемый

В B → ⋅ В ПРОТИВ → знак равно В B ¯ × В ЧАС ¯ знак равно В B × В ЧАС <\ displaystyle <\ overrightarrow > \ cdot <\ overrightarrow > = <\ overline > \ times <\ overline > = AB \ times AH>

Закон косинуса

Демонстрацию можно найти в подробной статье. Этот результат выражается через скалярное произведение:

Точечный продукт как площадь

Эта геометрическая форма имеет определенное преимущество, она позволяет установить алгебраические свойства скалярного произведения. Эти свойства полезны как для создания аналитического выражения, полезного для решения многих проблем, так и для создания новой формулировки, которая является как более общей, так и более функциональной.

Ортогональность, коллинеарность и угол

Алгебраические свойства

Симметрия

Основой этого определения является скалярное произведение, которое с двумя векторами связывает число.

Билинейность

Скалярное произведение в векторном пространстве E правильно совместимо со сложением. Это свойство означает, что скалярное произведение вектора на сумму двух векторов равно сумме двух скалярных произведений:

Симметрия скалярного произведения, а также совместимость справа демонстрируют совместимость слева от добавления:

Также можно говорить о совместимости справа для произведения скаляром. Это свойство принимает следующий вид:

Точка здесь обозначает как умножение на скаляр, так и скалярное произведение. Использование стрелок для обозначения векторов, а также греческих букв для обозначения чисел помогает избежать двусмысленности.

Как и прежде, следствием симметрии является совместимость слева:

Таким образом, приложение для a, которое связывает число с вектором, удовлетворяет следующему свойству: Икс → <\ displaystyle <\ vec >> y → <\ displaystyle <\ vec >> Икс → ⋅ y → <\ displaystyle <\ vec > \ cdot <\ vec >>

Положительно определенный характер

Скалярное произведение вектора на себя равно площади квадрата без учета длины одного из его представителей. В результате скалярное произведение вектора на самого себя всегда положительно. Это значение равно нулю тогда и только тогда, когда вектор равен нулю, потому что только нулевой вектор имеет представителя нулевой длины. Мы выводим следующие определения и предложения:

Баланс: реальный точечный продукт

Алгебраические свойства, наблюдаемые в случае размерности 2 или 3, достаточны для определения скалярного произведения в любом реальном векторном пространстве.

Мы говорим, что приложение

): & E \ times E & \ rightarrow & \ mathbb \\ & (x, y) & \ mapsto & (x \ mid y ) \ end <массив>>>

является скалярным произведением, если это:

Естественно задать обратный вопрос: можно ли определить геометрию, используя векторное пространство и скалярное произведение? Длина тогда определяется нормой, а угол θ между двумя ненулевыми векторами и формулой: Икс → <\ displaystyle <\ vec >> y → <\ displaystyle <\ vec >>

Евклидово пространство

Аналитическое выражение

Ортонормированный базис

В конечномерном векторном пространстве алгебраические свойства позволяют выразить скалярное произведение с помощью системы координат. Выражение упрощается, если выбранный базис ортонормирован (базисные векторы имеют норму, равную 1, и ортогональны два на два).

Икс → ⋅ y → знак равно Икс 1 y 1 + Икс 2 y 2 + Икс 3 y 3 <\ displaystyle <\ vec > \ cdot <\ vec > = x_ <1>y_ <1>+ x_ <2>y_ <2>+ x_ <3>y_ <3>> .

Это следует из развития скалярного произведения двух векторов, выраженных в основании:

которое по свойствам билинейности и симметрии записывается:

Написание матрицы

В ортонормированном базисе есть простой способ выразить скалярное произведение с помощью матриц. Тогда два вектора и из предыдущего абзаца принимают следующую форму: Икс → <\ displaystyle <\ vec >> y → <\ displaystyle <\ vec >>

Матрицы X и Y представляют два вектора. Используя транспонированную операцию и умножение матриц, получаем равенство:

Икс → ⋅ y → знак равно т Икс Y знак равно ( Икс 1 Икс 2 Икс 3 ) ( y 1 y 2 y 3 ) знак равно Икс 1 y 1 + Икс 2 y 2 + Икс 3 y 3 <\ displaystyle <\ vec > \ cdot <\ vec > = <> ^X

Y = <\ begin x_ <1>& x_ <2>& x_ <3>\ end > <\ begin y_ <1>\\ y_ <2>\\ y_ <3>\ end > = x_ <1>y_ <1>+ x_ <2>y_ < 2>+ x_ <3>y_ <3>>

Любая база

Обобщение на сложные векторные пространства

Эрмитово скалярное произведение

Чтобы адаптировать определение действительного скалярного произведения к комплексным векторным пространствам, нам понадобится понятие «полулинейности»:

Отображение f комплексного векторного пространства E в называется полулинейным, если оно удовлетворяет:

Мы говорим, что приложение : ( ∣ ) <\ Displaystyle (

)>

является левоэрмитовым скалярным произведением (или просто скалярным произведением ), если оно:

Доильбертовское пространство

Примеры

Эрмитское пространство

Гильбертово пространство

Источник

Скалярное произведение

Обычно используется одно из следующих обозначений:

, , ,

или (обозначение Дирака, часто применяемое в квантовой механике для векторов состояния):

.

Обычно предполагается, что скалярное произведение положительно определено, то есть

0″ border=»0″ /> для всех .

Если этого не предполагать, то произведение называется индефинитным.

Содержание

Определение

Скалярным произведением в векторном пространстве над полем комплексных (или вещественных) чисел называется функция для элементов , принимающая значения в (или ), определенная для каждой пары элементов и удовлетворяющая следующим условиям:

Действительное линейное пространство со скалярным произведением называется евклидовым, комплексное — унитарным.

Заметим, что из п.2 определения следует, что . Поэтому п.3 имеет смысл, несмотря на комплексные (в общем случае) значения скалярного произведения.

Элементарное определение

Элементарное определение скалярного произведения используется, когда определения длины вектора и угла между векторами введены независимым образом до введения понятия скалярного произведения (как правило, так и поступают при изложении элементарной геометрии). В этом случае скалярное произведение определяется через длины сомножителей и угол между ними:

Современная аксиоматика обычно строится начиная со скалярного произведения, и тогда длина вектора и угол определяются уже через скалярное произведение (см. ниже).

Связанные определения

В современном аксиоматическом подходе уже на основе понятия скалярного произведения векторов вводятся следующие производные понятия:

Примеры

Свойства

Неравенство Коши — Буняковского

Для любых элементов и линейного пространства со скалярным произведением выполняется неравенство [1]

История

Вариации и обобщения

Простейшим обобщением конечномерного скалярного произведения в тензорной алгебре является свёртка по повторяющимся индексам. Аналогичное обобщение в принципе нетрудно сделать и в бесконечномерном случае (Для бесконечномерных пространств функций — см. примеры (выше)).

См. также

Примечания

Ссылки

Полезное

Смотреть что такое «Скалярное произведение» в других словарях:

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ — отображение, сопоставляющее каждой паре е 1,е 2 векторов к. л. векторного пространства L нек роечисло (e1, е 2), причём выполняются след. условия:а) (*означает комплексное сопряжение); б) (e,e) = 0 лишь при е =0. Из этих аксиом следуют… … Физическая энциклопедия

скалярное произведение — — [http://www.rfcmd.ru/glossword/1.8/index.php?a=index&d=4180] Тематики защита информации EN scalar product … Справочник технического переводчика

скалярное произведение — векторов a и b, число (скаляр) (а, b), равное произведению длин этих векторов на косинус угла φ между ними, то есть (а, b) = |а||b|cosφ. Например, работа силы F вдоль прямолинейного отрезка S равна (F, S). * * * СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ СКАЛЯРНОЕ… … Энциклопедический словарь

скалярное произведение — skaliarinė sandauga statusas T sritis automatika atitikmenys: angl. inner product; internal product; scalar product vok. inneres Produkt, n; skalares Produkt, n; Skalarprodukt, n rus. внутреннее произведение, n; скалярное произведение, n pranc.… … Automatikos terminų žodynas

скалярное произведение — skaliarinė sandauga statusas T sritis fizika atitikmenys: angl. inner product; internal product; scalar product vok. inneres Produkt, n; Skalarprodukt, n rus. внутреннее произведение, n; скалярное произведение, n pranc. produit intérieur, m;… … Fizikos terminų žodynas

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ — векторов а и 6, число (скаляр) (а, b), равное произведению длин этих векторов на косинус угла ф между ними, т. е. (а, b)= |a||b| соs ф. Напр., работа силы F вдоль прямолинейного отрезка S равна (F, S) … Естествознание. Энциклопедический словарь

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ — внутреннее произведение ( а, b).ненулевых векторов a и b, произведение их модулей на косинус угла j между ними: ( а, b) = | а || b| cos j. За j принимается угол между векторами, не превосходящий p. Если a=0 и b=0, то С. п. полагают равным нулю. С … Математическая энциклопедия

Скалярное произведение — векторов а и b, Скаляр, равный произведению длин этих векторов и косинуса угла между ними; обозначается (а, b) (или ab). Например, работа постоянной силы F вдоль прямолинейного пути S равна (F, S). Свойства С. п.: 1) (а, b) = (b, а), 2)… … Большая советская энциклопедия

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ — векторов а и Ь число (скаляр), равное произведению длин этих векторов на косинус угла ф между ними: (а, b) = ab = |a| lbt cos ф. Напр., работа А постоянной силы F при смещении а точки её приложения равна А = Fs. Понятие С. п. обобщают на n мерное … Большой энциклопедический политехнический словарь

Источник

Скалярное произведение векторов и его свойства

Скалярным произведением двух ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними. Если хотя бы один из двух векторов нулевой, то угол между ними не определён, а скалярное произведение считается равным нулю. Скалярное произведение векторов и обозначается

Скалярное произведение вектора самого на себя называется скалярным квадратам.

Решение. По определению находим

Геометрический смысл скалярного произведения векторов

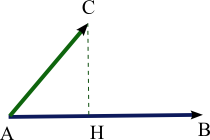
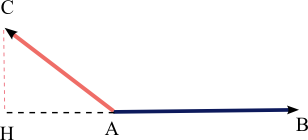
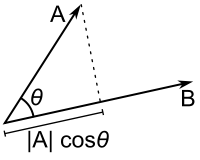
Рассмотрим ортогональную проекцию ненулевого вектора на ось, задаваемую вектором (рис. 1.37). Согласно пункту 1 замечаний 1.4, алгебраическое значение длины проекции равно произведению длины вектора на косинус угла между векторами и :

Алгебраические свойства скалярного произведения

Для любых векторов и любого действительного числа :

Первое свойство определяет симметричность скалярного произведения, второе и третье — аддитивность и однородность по первому множителю, четвертое свойство — неотрицательность скалярного квадрата. Эти свойства аналогичны свойствам произведения чисел: первое свойство соответствует закону коммутативности умножения чисел, второе — закону дистрибутивности умножения по отношению к сложению, третье — закону ассоциативности умножения. Поэтому рассматриваемая операция и называется произведением векторов. Поскольку ее результатом является число (скаляр), то такое произведение векторов называется скалярным.

1. Свойства аддитивности и однородности скалярного произведения означают линейность скалярного произведения по первому множителю :

3. Для любых векторов справедливо неравенство Коши — Буняковского

4. Из неравенства Коши — Буняковского следует неравенство треугольника (длина стороны треугольника меньше суммы длин двух других его сторон и больше модуля их разности):

Геометрические свойства скалярного произведения

С помощью скалярного произведения можно находить основные метрические величины: длины отрезков (или, что то же самое, длины векторов) и величины углов.

2. Величина угла между ненулевыми векторами находится по формуле:

Отсюда заключаем, что:

— ненулевые векторы и перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю: ;

— угол между ненулевыми векторами и острый тогда и только тогда, когда их скалярное произведение положительно;

— угол между ненулевыми векторами и тупой \frac<\pi><2>\right)» png;base64,iVBORw0KGgoAAAANSUhEUgAAAFIAAAAmBAMAAAClsdF/AAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAAZvHEYFEYuAx8CFysX6e75gAAAHwSURBVDjLY2AgCbCY4JBgFBQUZGBwcoALOE/ArtDpHRAUMLAjDLLBYaJRsGpTjAMDoy5MhNUAu0r2AuGNC0EMjgNQkX0JuDywQ/ohWMsSKF8Zp1eD2MBmMjZBuNzPcSlkXM4GNpOhbgOYYlqISyX7E56XYIZfAJiSUsClksOA7SmYIdwIpvIKcKnkTWC4BmZAjY7bgNNHAlCa7Q2YshMgGN2Mb8HkYhTBMGz6GFeARBkfowi6mmNRygi2l+0RiD2NgaH4JljQ1cYBU+k9kF8gAWHCwNTcATHNxxRTaVwCTCX7AYZaBw9o4hM33YBbpbADowkDMyyZijeBTGVRAgN1NJUMYgUMEjC/iBmBVIpgVSkhwLuB4RDcSLDtjFhtlyjwEBBvgTkTn4/YHivnWECc6dqKLZRActzgkJ/87lUIoZBnXAwm10BNUkdW6BMDCS9GSFCD1Yu9xhLdnOaHlyOlEIY4kBuYFmBLyRNY1oEdz/kGkZKFL2BROW8Jg14AUkoG5w5OLB5m2LWQIQ5cFvA2EshxjAIMeuBCwQ+S1bif4SnbVjkg5WJG3CUDA9NK5JIBT2nDUAX2OttqAiUY0J+d4OwpASvBGExxqZzswAbySyzBkpazLS0JGJ5sJgRLb2dgkQz0w2YHggXCZGNjY7h1ACJhdRVcflHKAAAAAElFTkSuQmCC» style=»vertical-align: middle;» /> тогда и только тогда, когда их скалярное произведение отрицательно.

Свойства 1 и 2 следуют непосредственно из определения скалярного произведения. Третье и четвертое свойства вытекают из геометрического смысла скалярного произведения (см. (1.8)) и п.1 замечаний 1.4.

Пример 1.14. Доказать тождества

Решение. Используя коммутативность и линейность скалярного произведения, запишем равенства

Заменяя скалярные квадраты векторов квадратами их длин (см. геометрическое свойство 1), получаем

Если из первого равенства вычесть второе, то придем к тождеству (а). Если же сложить оба равенства, то получим тождество (б).

Доказанные равенства выражают следующие свойства параллелограмма, построенного на векторах и ( и — его диагонали):

а) скалярное произведение векторов равно одной четвертой от разности квадратов диагоналей параллелограмма, построенного на множителях;

б) сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.

Источник