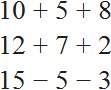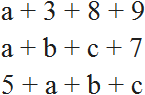Что такое сложное выражение в математике

Урок математики во 2-м классе «Сложные выражения без скобок с действиями разных степеней и порядок выполнения в них действий»

Ход урока

1. Организационный момент

Долгожданный дан звонок.
Начинается урок.

2. Актуализация опорных знаний

Учитель: Сегодня на уроке математики мы:

– проведем математическую разминку;
– получим новые знания;
– продолжим работу с задачами.

– Предлагаю начать урок с математической разминки.

– Ребята, что вы можете сказать о данных числах?

(- натуральные числа;
– 28, 25, 22 – двузначные числа, а 276 – трехзначное число;
– 276 – “лишнее” число;
– в записи каждого числа использована цифра “2”)

– Запишите, пожалуйста, двузначные числа в тетрадь.

– Что вы заметили? (Есть ли в числовом ряду какая-то закономерность?)

(- числа расположены в порядке уменьшения;
– каждое следующее число на 3 меньше, чем предыдущее).

– Пригодилось ли вам умение выполнять действия разных ступеней в выражениях без скобок? (Да.)

8. Итог урока. Рефлексия

– Наш урок подошел к концу.

– Какое же открытие вы сделали на уроке? (Научились выполнять действия разных ступеней в выражениях без скобок?)

– Только ли при решении выражений необходимы эти знания? ( Нет. Они нужны и при решении задач.)

– Что вам кажется самым главным на этом уроке?

– Кто испытал затруднения на уроке и в чем?

– Кто запомнил, какое открытие нас ждет на следующем уроке? (Познакомимся с порядком выполнения действий в выражениях со скобками, содержащих действия одной или разных ступеней.)

– Что больше всего понравилось в уроке?

– А мне понравилось, как вы сегодня работали на уроке. Спасибо!

Источник

Выражения

Выражение — это любое сочетание чисел, букв и знаков операций. Можно сказать, что вся математика состоит из выражений.

Выражения бывают двух видов: числовые и буквенные.

Числовые выражения состоят из чисел и знаков математических операций. Например, следующие выражения являются числовыми:

Буквенные выражения помимо чисел и знаков операций содержат ещё и буквы. Например, следующие выражения являются буквенными:

Буквы, которые содержатся в буквенных выражениях, называются переменными. Запомните это раз и навсегда! Спросите любого школьника что такое переменная — этот вопрос поставит его в ступор, несмотря на то что он будет решать сложные задачи по математике, не зная что это такое. А между тем, переменная это фундаментальное понятие, без понимания которого математику невозможно изучать.

Под словом «изучать» мы подразумеваем самостоятельное чтение соответствующей литературы и способность понимать, что там написано. А то вроде и знаешь математику на четвёрку, задачи решаешь, но не можешь понять, что написано в лекциях и книгах. Каждому знакомо такое чувство, особенно студентам.

Поскольку понятие переменной очень важно, остановимся на нём подробнее. Посмотрите внимательно на слово «переменная». Ничего не напоминает? Слово «переменная» происходит от слов «меняться», «изменить», «изменить своё значение». Переменная в математике всегда выражена какой-то буквой. Например, запишем следующее выражение:

Значение переменной a подставляется в исходное выражение.

В результате имеем: 5 + 5 = 10

Конечно, мы рассмотрели простейшее выражение. На практике встречаются более сложные выражения, в которых присутствуют дроби, степени, корни и скобки. Выглядит это устрашающе. На самом деле ничего страшного. Главное понять сам принцип.

Значение переменной x подставляется в выражение x + 10

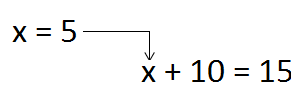
Переменная это своего рода контейнер, где хранится значение. Переменные удобны тем, что они позволяют, не приводя примеров доказывать теоремы, записывать различные формулы и законы.

Имея выражение a + b = c, можно пользоваться им, подставляя вместо переменных a и b любые числа. А переменная c будет получать своё значение автоматически, в зависимости от того, какие числа будут подставлены вместо a и b

Решение:

Значение выражения

Фраза « выполнить действие » означает выполнить одну из операций действия.

Значение выражения — это результат выполнения действий, содержащихся в выражении.

Рассмотрим еще примеры:

Источник

Урок математики по теме «Сложные выражения»

Выбранный для просмотра документ Конспект урока.docx

Урок математики в 3 классе «Порядок действий в сложных выражениях»

Тема урока: «Порядок действий в сложных выражениях»

Тип урока : урок систематизации знаний

учебная: формировать умения решать сложные выражения, определять порядок действия в числовых выражениях без скобок и со скобками

воспитательная: расширение и укрепление ценностно-смысловой сферы: сотрудничество, общение, взаимовыручка, товарищество; побуждение учеников к самоанализу своей деятельности;

развивающая: формирование умения сравнивать, анализировать, обобщать;

·формирование умения вести диалог, высказывать свои мысли.

Личностные: способствовать созданию условий для осознания значимости своей деятельности в учебном процессе; умения высказывать и отстаивать свою точку зрения.

Регулятивные: создавать условия для формирования умения ставить учебные цели и задачи и добиваться их реализации, планировать свою деятельность и оценивать результат своих действий.

Познавательные: содействовать развитию умения исследовать и анализировать полученную информацию по теме, с целью выделения отличительных признаков и критериев, необходимых для сравнения и анализа.

Коммуникативные: создавать условия для развития устной речи учащихся, умения слушать и вступать в диалог, интегрироваться в группы и строить продуктивное сотрудничество, учиться на принципах толерантности обсуждать вопросы, учитывать позиции других людей.

Способствовать формированию умения находить значения сложных выражений, зная алгоритм и правила порядка выполнения действий.

Формы роботы: фронтальная, групповая, индивидуальная

— Здравствуйте, ребята! Я рада приветствовать вас на уроке математики.

И чтобы у нас все сегодня получилось, давайте скажем следующие слова:

— Я умный, способный и у меня все получится

— А теперь улыбнитесь друг другу и садитесь на свои места.

2. Актуализация опорных знаний

Нам сегодня на уроке придётся очень много считать.

Проведём РАЗМИНКУ (Приложение 1) и определим Лидеров Быстрого и правильного счёта!

524 + 378 814 – 276 329 * 6 428 : 2

(У детей карточка-разминка, они решают примеры разминки в тетради, проверяют себя по ключу(он на обратной стороне листа) и если все 4 примера решены верно, ребёнок встаёт. Учитель озвучивает его место – 1-й. 2-й. 3-й и т.д. Ребёнок фиксирует на полях тетради какое место он занял. Затем он составляет и решает СВОИ ПРИМЕРЫ, пока другие дети продолжают решать разминку. Если ребёнок допустил ошибки в вычисления и узнал о них при проверке по ключу, то он выполняет работу над ошибками, только потом имеет право встать. Таким образом определяются Лидеры Быстрого и Правильного Счёта!)

Встаньте 10-ка Лидеров Быстрого и Правильного Счёта! 5-ка!

В предыдущем домашнем задании, где нужно было найти значение выражений, у некоторых ребят были допущены ошибки. Логические, в определении порядка действий, и– вычислительные. Выполним задания, которые вам помогут решать числовые выражения без ошибок.

Давайте для начала вспомним правила «Порядок выполнения действий в числовых выражениях».

Учитель показывает карточку(+/-) (Приложение 3). (У детей на партах такие же мини-карточки).

1. Если числовое выражение содержит только действия сложения и вычитания, то….

(Правило произносит один ученик, затем дети его проговаривают друг другу в парах)

Учитель показывает карточку(*/:)(Приложение 3)

2. Если числовое выражение содержит только действия умножения и деления, то…

(Правило произносит один ученик, затем дети его проговаривают друг другу в парах)

Учитель показывает карточки (+/- и */:) (Приложение 3)

3. Если числовое выражение содержит не только сложение и вычитание, но и умножение с делением, то…

(Правило произносит один ученик, затем дети его проговаривают друг другу в парах)

Учитель показывает карточку ( ( ) )(Приложение 3)

4.Если запись выражения содержит одну или несколько пар скобок, то …

(Правило произносит один ученик, затем дети его проговаривают друг другу в парах)

(Один ребёнок делает такое же задание и доски с крупными карточками).

Проговорите алгоритм в парах друг другу.

Образец правильного алгоритма:

и расставьте действия над ними;

2. Найдите действия * и : расставьте действия над ними слева направо;

3. Расставьте действия над знаками

Расставьте порядок действий в выражениях, пользуясь знаниями алгоритма (Приложение 5):

Проверьте по ключу ( ключ на обратной стороне).

«Составьте программу вычисления значения выражения и найдите значение этого выражения» (в группах)

(Каждому ряду предлагается найти значение выражения своего выражения. Группа из 4-х ребят, каждый ребёнок выполняет одно из действий выражения)

Выполняйте работу по алгоритму, осуществляя пошаговый контроль:

1. Прочтите задание.

2. Распределите обязанности в группе.

3. Выполните задание.

4. Прикрепите его на доске!

1 ряд: 6 * 5 : 10 * 9 : 27 * 8

2 ряд: 16 * 2 – 35 : 7 + 73

3 ряд: 360 : ( 47 – 19 * 2)+1

(На доске висят карточки со следующими значениями: 7 8 100 10 41 14)

( В результате проверки данного задания, карточки со значениями переворачиваются, и получается высказывание М.Ломоносова)

8 = Кто малого не может, 100 = тому и большее невозможно. 41= Ломоносов.

Кто малого не может, тому и большее невозможно. Ломоносов. (Презентация слайд 1)

— Его именем назван самое известное учебное заведение нашей страны – МГУ, чтобы попасть в него учиться, нужно очень хорошо учиться.

-Кто хочет в будущем учиться в МГУ? Отличное желание!

3. Постановка учебной проблемы, формулирование темы урока.

— На доске схематичная запись: 3 * (4 + 3) : 3 + 60 : (6 + 4) * 5 – 12 =

Как вы думаете будет звучать тема нашего урока? ( Порядок действий в сложных выражениях)

-Что важно знать при решении сложных выражений, содержащих много действий и скобки?

(Необходимо знать алгоритм и правила нахождения значений выражений. Они помогут определять порядок действий в сложных выражениях )

Составляем программу действий

3 * (4 + 3) : 3 + 60 : (6 + 4) * 5 – 12 =

Если программа действий составлена правильно, можно ли утверждать, что каждый ученик верно справится с нахождением значения данного выражения? Где могут допустить ученики ошибку?

Есть рациональный способ решения сложных числовых выражений – деление его на блоки! (Презентация слайд 2)

(Фронтальная работа – нахождение значения данного выражения)

Физкультминутка (проводят ученики класса)

Наклонились, ну-ка, ну-ка!

А теперь назад прогнулись.

Разминаем руки, плечи,

Чтоб сидеть нам было легче,

Чтоб писать, читать, считать

И совсем не уставать.

Голова устала тоже.

Так давайте ей поможем!

Вправо-влево, раз и два.

Думай, думай, голова.

Хоть зарядка коротка,

Отдохнули мы слегка.

4. Систематизация знания

13 * 10 + (64 – 18 + 24) : 10 – 5 * 0

Посмотрим, как вы справитесь с решением данного выражения. Есть смелые ребята, желающие его решить у доски?

Те, кому трудно решайте, опираясь на образец решения ученика, работающего у доски.

Те, кому легко, вы решаете данное выражение самостоятельно и можете выполнить ещё дополнительное выражение

(карточка у детей на партах)

3 * (4 + 3) : 3 – 53 * (4 + 3) : 3 – 5

– Ребята, где нам может пригодиться умение находить значение сложного выражения? (Решать задачи)

Купили 3 м шерстяной ткани, по 100 рублей за метр, и столько же метров льняной ткани, по 50 рублей за метр. Сколько денег израсходовали на всю покупку?

— О чём говорится в задаче?

-Как предлагаете оформить краткую запись?

Цена Кол-во Стоимость

-Восстановим в памяти формулу нахождения стоимости.

-Можно ли решить данную задачу, составив выражение?

100 * 3 + 50 * 3 =300+150=450(руб)

(100 + 50) * 3 =150 * 3=450 (руб)

Ответ: 450 рублей израсходовали на всю покупку.

5.Включение новых знаний в систему знаний

Самостоятельная работа (Приложение 6)

Проверка умения находить значения выражений в несколько действий.

Предлагаю выполнить самостоятельную работу. Она состоит из трёх уровней. От уровня А к С задания усложняются. Уровень С – задания олимпиадного характера. Каждый из вас может выбрать и решить карточку любого уровня. Начать предлагаю с того уровня, который вам наиболее интересен. После выполнения одного уровня нужно проверить себя по ключу, только потом переходить к выполнению заданий следующего уровня.

(Карточки каждого уровня различаются по цвету).

( 91 – 83 ) • 3 : 4 + 12 : 6

42 : 6 + ( 19 + 6 ) : 5 – 6 • 2

60 – (13 + 22 ) : 5 – 6 • 4 + 25

7 • 6 + 9 • 4 – ( 2 • 7 + 54 : 6 • 5 )

( 27 – 19 ) • 4 + 18 : 3 + ( 8 + 27 ) : 5 – 17

( 9 • 7 + 56 : 7) – ( 2 • 6 – 4 ) • 3 + 54 : 9

Расставь скобки в выражении так, чтобы его значение было равно числу:

48 : 4 + 8 * 7 – 5 = 63

48 : 4 + 8 * 7 – 5 = 23

48 : 4 + 8 * 7 – 5 = 135

6. Итог урока. Рефлексия

Учащиеся высказываются одним предложением, выбирая начало фразы из рефлексивного экрана на экране (Презентация слайд 3):

Проверь правильность выполнения самостоятельной работы!

Исходя из этого, ты получаешь индивидуальное д/з (Приложение 7)

Тех ребят, которые справились с самым сложным заданием – карточкой Уровня С – ждёт задание со ****. (Приложение 8)

Источник

Чем отличается простое выражение от сложного?

Чем отличается простое выражение от сложного.

Сложное это когда большое предложения а простое когда маленькое.

1) Найдите значение выражений?

1) Найдите значение выражений.

2)Составить из простых выражений сложное выражение и запиши его значение.

Что такое простое выражение и что такое сложное выражение?

Что такое простое выражение и что такое сложное выражение!

ЭТО ОЧЕНЬ СРОЧНО ДАЮ 30БАЛОВ.

Запиши простые выражения, из которых составлено данное сложное выражение?

Запиши простые выражения, из которых составлено данное сложное выражение.

Чему равно значение сложного выражения?

Преобразуйте простое выражение в несколько вариантов сложного по заданным схемам?

Преобразуйте простое выражение в несколько вариантов сложного по заданным схемам.

Запиши простые выражения, из которых составлено данное сложное выражение?

Запиши простые выражения, из которых составлено данное сложное выражение.

Банк выплачивает вкладчикам 16% годовых?

Банк выплачивает вкладчикам 16% годовых.

Вклад составляет 18000.

На какую сумму будут отличаться вклады при простом и сложном процентном росте?

Источник

Приоритет операций. Cложные математические выражения

Пожалуйста, приостановите работу AdBlock на этом сайте.

В C используется знакомый нам со школы порядок выполнения операций. Но т.к. в программировании есть свои особенности, то кое-какие отличия всё же есть. Выпишем приоритет для тех операций, которые мы уже знаем.

А каково значение переменной x после выполнения следующего кода int x = 8 / 4 / 2;

Правильный ответ 1. Т.к в случае одинакового приоритета операций, команды выполняются слева направо. Другими словами данный код эквивалентен коду int x = (8 / 4) / 2;

Если нам нужно изменить порядок выполнения действий, то мы можем использовать для этого круглые скобки.

На следующем рисунке над каждым действием отмечено, каким оно выполнится по счёту.

Рис.1 Приоритет операций в языке С. Пример.

Если в вашей программе вы написали довольно сложное выражение, в котором не сразу ясен порядок операций, то лучше добавить лишние скобки, чтобы явно задать последовательность операций. Это поможет избежать ошибок в вычислениях, которые потом будет сложно отловить.

Сложные математические выражения

Иногда формулы, по которым нужно что-то вычислять, в программе могут принимать довольно ужасный вид.

При этом когда мы пишем программу, любая формула должна быть записана в одну строку. На начальном этапе это может вызвать у вас некоторые затруднения. Чтобы избавиться от этих затруднений, нужно овладеть навыком переводить формулу из стандартной математической записи в ту, которая используется в программировании и обратно.

И небольшой видео-фрагмент, в котором я попытался на простом примере показать, как можно поступать при записи сложных математических выражений.

Практика

Решите предложенные задачи:

Для удобства работы сразу переходите в полноэкранный режим

Источник