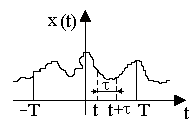Что такое случайный процесс

Случайный процесс

Случа́йный проце́сс (случайная функция) в теории вероятностей — семейство случайных величин, индексированных некоторым параметром, чаще всего играющим роль времени или координаты.
Другое определение:
Случайным называется процесс u(t), мгновенные значения которого являются случайными величинами.

Содержание

Определение

Пусть дано вероятностное пространство . Параметризованное семейство случайных величин

,

где произвольное множество, называется случайной функцией.

Терминология

Данная классификация нестрогая. В частности, термин «случайный процесс» часто используется как безусловный синоним термина «случайная функция».

Классификация

Траектория случайного процесса

Пусть дан случайный процесс . Тогда для каждого фиксированного — случайная величина, называемая сечением. Если фиксирован элементарный исход , то — детерминистическая функция параметра . Такая функция называется траекто́рией или реализа́цией случайной функции .

Примеры

является случайным процессом.

Примечания

См. также

Источники

Полезное

Смотреть что такое «Случайный процесс» в других словарях:

случайный процесс — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] случайный процесс вероятностный процесс стохастический процесс Случайная функция X(t) от независимой переменной t (в экономике она чаще всего интерпретируется как время). Иначе … Справочник технического переводчика

СЛУЧАЙНЫЙ ПРОЦЕСС — (вероятностный или стохастический), процесс изменения во времени состояния или характеристик некоторой системы под влиянием различных случайных факторов, для которого определена вероятность того или иного его течения. Типичным примером случайного … Большой Энциклопедический словарь

Случайный процесс — [random process] (вероятностный, стохастический процесс) случайная функция X(t) от независимой переменной t (в экономике она чаще всего интерпретируется как время). Иначе говоря, это такой процесс, течение которого может быть различным в… … Экономико-математический словарь

СЛУЧАЙНЫЙ ПРОЦЕСС — функция 2 х аргументов X(t)= X(ω,t); множество элементарных событий, параметр, обычно интерпретируемый как время. Для каждого tX(ω,t) функция только ω и представляет собой случайную величину. Для фиксированного ω X(ω,t)… … Геологическая энциклопедия

Случайный процесс — 1. Случайный процесс Вероятностный процесс Источник: ГОСТ 21878 76: Случайные процессы и динамические системы. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации

случайный процесс — (вероятностный, или стохастический), процесс изменения во времени состояния или характеристик некоторой системы под влиянием различных случайных факторов, для которого определена вероятность того или иного его течения. Типичным примером… … Энциклопедический словарь

Случайный процесс — (вероятностный, или стохастический) процесс (т. е. изменение во времени состояния некоторой системы), течение которого может быть различным в зависимости от случая и для которого определена вероятность того или иного его течения. Типичным … Большая советская энциклопедия

СЛУЧАЙНЫЙ ПРОЦЕСС — (вероятностный, или стохастический), процесс изменения во времени состояния или характеристик нек рой системы под влиянием разл. случайных факторов, для к рого определена вероятность того или иного его течения. Типичным примером С. п. может… … Естествознание. Энциклопедический словарь

случайный процесс — tikimybinis procesas statusas T sritis chemija apibrėžtis Procesas, kuris iš anksto negali būti tiksliai nusakytas, o yra apibūdinamas jo vykimo tikimybe. atitikmenys: angl. probabilistic process; random process; stochastic process rus.… … Chemijos terminų aiškinamasis žodynas

Источник

Случайные процессы и функции

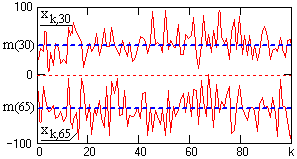
Случайный процесс Х(t) представляет собой функцию, которая отличается тем, что ее значения в любые произвольные моменты времени по координате t являются случайными. Строго с теоретических позиций, случайный процесс X(t) следует рассматривать как совокупность множества реализаций функций x_k(t), имеющих общую статистическую закономерность. При регистрации случайного процесса на определенном временном интервале осуществляется фиксирование единичной реализации x_k(t) из бесчисленного числа возможных реализаций процесса X(t). Эта единичная реализация называется выборочной функцией случайного процесса X(t). Примеры выборочных функций модельного случайного процесса X(t) приведены на рис. 131. В дальнейшем без дополнительных пояснений при рассмотрении различных параметров и характеристик случайных процессов для сопровождающих примеров будем использовать данную модель процесса.

Рис. 13.1. Выборочные функции случайного процесса.

С практической точки зрения выборочная функция является результатом отдельного эксперимента, после которого данную реализацию x_k(t) можно считать детерминированной функцией. Сам случайный процесс в целом должен анализироваться с позиции бесконечной совокупности таких реализаций, образующих статистический ансамбль. В каждый выбранный момент времени t₁ конкретная реализация процесса представляет собой случайную величину х₁ с определенной плотностью вероятности p(x₁, t₁), а ее среднее значение определяется усреднением по всем возможным реализациям в этот момент времени t₁. Полной статистической характеристикой такой системы является N-мерная плотность вероятностей р(x_n; t_n). Однако, как экспериментальное определение N-мерных плотностей вероятностей процессов, так и их использование в математическом анализе представляет значительные математические трудности. Поэтому на практике обычно ограничиваются одно- и двумерной плотностью вероятностей процессов.

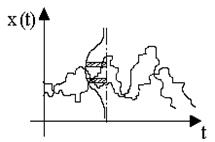
Рис. 13.2. Сечения случайного процесса X(t).

Одномерная функция распределения вероятностей (x, t_n) определяет вероятность того, что в момент времени t_n значение случайной величины X(t_n) не превысит значения x:

Очевидно, что в диапазоне значений вероятностей от 0 до 1 функция F(x, t) является неубывающей с предельными значениями F(-¥, t) = 0 и F(¥, t) = 1. При известной функции F(x, t) вероятность того, что значение X(t_n) в выборках будет попадать в определенный интервал значений [a, b] будет определяться выражением:

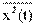
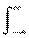
P(a 2 (t)>º = x 2 p(x; t) dx.

Функция дисперсии (variance) – второго центрального момента случайного процесса, определяет функцию среднего взвешенного значения (математического ожидания) квадрата разности Х(t)-m_x(t), которая называется флюктуационной частью процесса:

D_x(t) = M<[Х(t)-m_x(t)] 2 > = 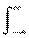[x(t)-m_x(t)] 2 p(x; t) dx. (

Функция среднего квадратического отклонения (standard deviation) служит амплитудной мерой разброса (флюктуаций) значений случайного процесса по временной оси относительно математического ожидания процесса:

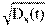
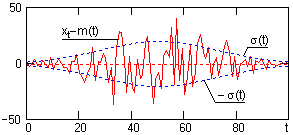
s_x(t) = . (13.3)

На рис. 13.4 приведен пример флюктуационной составляющей процесса X(t) (рис. 13.1) в одной из реализаций в сопоставлении со средним квадратическим отклонением ±s случайных величин от математического ожидания m(t).

p(x) = .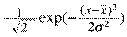

Это определяется тем, что в соответствии с «центральной предельной теоремой» распределение вероятностей для сумм независимых случайных величин, при которых нет доминирующих, стремится к нормальному закону по мере роста числа слагаемых, и не зависит от законов распределения слагаемых. Между тем физические случайные процессы обычно являются многопараметровыми, при этом случайность значений параметров, как правило, обусловлена их природой и также соответствует нормальным распределениям.

Двумерная плотность вероятностей. Одномерные законы плотности распределения вероятностей случайных процессов не несут каких-либо характеристик связи между значениями случайных величин для различных значений аргументов.

Двумерная плотность вероятностей p(x₁,x₂; t₁,t₂) определяет вероятность совместной реализации значений случайных величин Х(t₁) и Х(t₂) в произвольные моменты времени t₁ и t₂ и в какой-то мере уже позволяет оценивать динамику развития процесса. Двумерная плотность вероятностей описывает двумерную случайную величину n), X(t_m)> в виде функции вероятности реализации случайной величины X(t_n) в бесконечно малом интервале dx_n в окрестностях x_n в момент времени t_n при условии, что в момент времени t_m значение X(t_m) будет реализовано в бесконечно малом интервале dx_m в окрестностях x_m:

При двумерной плотности вероятности имеем:

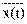
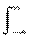
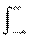
m_x(t) º = x₁(t₁) p(x₁,t₁; x₂,t₂) dx₁ dx₂. (13.1″)

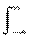
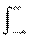
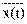
D_x(t) = s_x 2 (t)= [x₁(t₁)- ] 2 p(x₁,t₁; x₂,t₂) dx₁ dx₂. (13.2″)

Корреляционные функции случайных процессов. Характеристикой динамики изменения двумерной случайной величины n), X(t_m)> является корреляционная функция, которая описывает случайный процесс в целом:

Корреляционная функция представляет собой статистически усредненное произведение значений случайного процесса X(t) в моменты времени t_n и t_m по всем значениям аргументов t_n и t_m, а, следовательно, тоже является двумерной функцией. В терминах теории вероятностей корреляционная функция является вторым начальным моментом случайного процесса.

На рис. 13.5 приведены примеры реализаций двух случайных процессов, которые характеризуются одной и той же функцией математического ожидания и дисперсии.

Рис. 13.5.

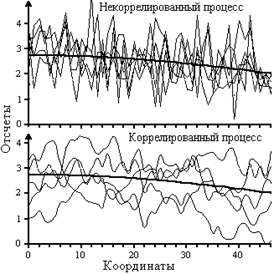
На рисунке видно, что хотя пространство состояний обоих процессов практически одно и то же, динамика развития процессов в реализациях существенно различается. Единичные реализации коррелированных процессов в произвольный момент времени могут быть такими же случайными, как и некоррелированных, а в пределе, во всех сечениях оба процесса могут иметь один и тот же закон распределения случайных величин. Однако динамика развития по координате t (или любой другой независимой переменной) единичной реализации коррелированного процесса по сравнению с некоррелированным является более плавной, а, следовательно, в коррелированном процессе имеется определенная связь между последовательными значениями случайных величин. Оценка степени статистической зависимости мгновенных значений какого-либо процесса Х(t) в произвольные моменты времени t_n и t_m и производится функцией корреляции. По всему пространству значений случайного процесса X(t) корреляционная функция определяется выражением:

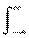
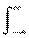
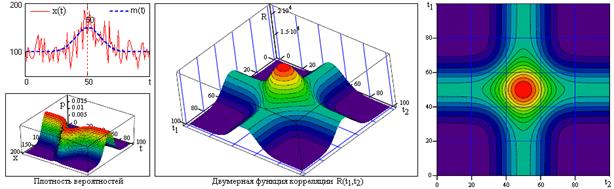
R_X(t_n, t_m) = x(t_n)x(t_m) p(x_n,t_m; x_n,t_m) dx_n dx_m, (9.1.4)

Рис. 13.6. Двумерная плотность вероятностей и корреляционная функция процесса X(t).

На рис. 13.6 приведена форма модельного случайного процесса X(t) в одной выборке со значительной и изменяющейся неслучайной составляющей. Модель задана на интервале 0-Т (Т=100) в дискретной форме с шагом Dt=1. Корреляционная функция вычислена по заданной плотности вероятностей модели.

При анализе случайных процессов второй момент времени t_m удобно задавать величиной сдвига t относительно первого момента, который при этом может быть задан в виде координатной переменной:

Функция, задаваемая этим выражением, обычно называется функцией автокорреляции случайного процесса.

Ковариационные функции. Частным случаем корреляционной функции является функция автоковариации (ФАК), которая широко используется при анализе сигналов. Она представляет собой статистически усредненное произведение значений центрированной случайной функции X(t)-m_x(t) в моменты времени t_n и t_m и характеризует флюктуационную составляющую процесса:

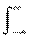
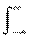
К_Х(t_n,t_m) = (x(t_n)-m_x(t_n)) (x(t_m)-m_x(t_m)) p(x_n,t_n; x_m,t_m) dx_n dx_m, (13.5)

В терминах теории вероятностей ковариационная функция является вторым центральным моментом случайного процесса. Для центрированных случайных процессов ФАК тождественна функции корреляции. При произвольных значениях m_x ковариационные и корреляционные функции связаны соотношением:

Нормированная функция автоковариации (функция корреляционных коэффициентов):

При t= 0 значение r_Х равно 1, а ФАК вырождается в дисперсию случайного процесса:

Отсюда следует, что для случайных процессов и функций основными характеристиками являются функции математического ожидания и корреляции (ковариации). Особой необходимости в отдельной функции дисперсии не имеется.

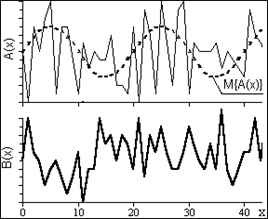
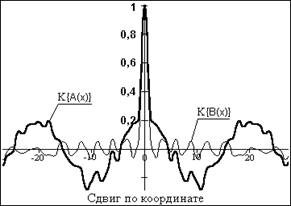
Примеры реализаций двух различных случайных процессов и их нормированных ковариационных функций приведены на рис. 13.7.

Рис. 13.7. Реализации и ковариационные функции случайных процессов.

Источник

Случайный процесс

Полезное

Смотреть что такое «Случайный процесс» в других словарях:

случайный процесс — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] случайный процесс вероятностный процесс стохастический процесс Случайная функция X(t) от независимой переменной t (в экономике она чаще всего интерпретируется как время). Иначе … Справочник технического переводчика

СЛУЧАЙНЫЙ ПРОЦЕСС — (вероятностный или стохастический), процесс изменения во времени состояния или характеристик некоторой системы под влиянием различных случайных факторов, для которого определена вероятность того или иного его течения. Типичным примером случайного … Большой Энциклопедический словарь

Случайный процесс — [random process] (вероятностный, стохастический процесс) случайная функция X(t) от независимой переменной t (в экономике она чаще всего интерпретируется как время). Иначе говоря, это такой процесс, течение которого может быть различным в… … Экономико-математический словарь

СЛУЧАЙНЫЙ ПРОЦЕСС — функция 2 х аргументов X(t)= X(ω,t); множество элементарных событий, параметр, обычно интерпретируемый как время. Для каждого tX(ω,t) функция только ω и представляет собой случайную величину. Для фиксированного ω X(ω,t)… … Геологическая энциклопедия

Случайный процесс — 1. Случайный процесс Вероятностный процесс Источник: ГОСТ 21878 76: Случайные процессы и динамические системы. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации

Случайный процесс — (случайная функция) в теории вероятностей семейство случайных величин, индексированных некоторым параметром, чаще всего играющим роль времени или координаты. Другое определение: Случайным называется процесс u(t), мгновенные значения… … Википедия

случайный процесс — (вероятностный, или стохастический), процесс изменения во времени состояния или характеристик некоторой системы под влиянием различных случайных факторов, для которого определена вероятность того или иного его течения. Типичным примером… … Энциклопедический словарь

СЛУЧАЙНЫЙ ПРОЦЕСС — (вероятностный, или стохастический), процесс изменения во времени состояния или характеристик нек рой системы под влиянием разл. случайных факторов, для к рого определена вероятность того или иного его течения. Типичным примером С. п. может… … Естествознание. Энциклопедический словарь

случайный процесс — tikimybinis procesas statusas T sritis chemija apibrėžtis Procesas, kuris iš anksto negali būti tiksliai nusakytas, o yra apibūdinamas jo vykimo tikimybe. atitikmenys: angl. probabilistic process; random process; stochastic process rus.… … Chemijos terminų aiškinamasis žodynas

Источник

Общие сведения о случайных процессах

Случайная функция, зарегистрированная в той или иной форме по результатам опыта, называется реализацией случайной функции. Случайная функция x, для которой независимой переменной является время t, называется случайным или стохастическим процессом. Этот процесс можно отобразить в виде реализаций случайной функции (рис.9.2).

Случайный процесс не есть определенная кривая x(t), а является множеством кривых x(t), так же как случайная величина не имеет определенного значения, а является совокупностью (множеством) возможных значений.

Можно сказать, что случайный процесс есть такая функция времени, значение которой в каждый момент времени является случайной величиной.

Рис. 9.2. Реализации случайного процесса

В случайном процессе нет определенной зависимости x(t). Каждая кривая множества (рис.9.2) является лишь отдельной реализацией случайного процесса. Никогда нельзя сказать заранее, по какой кривой пойдет процесс.

Чтобы судить о возможном характере протекания случайного процесса, введены вероятностные характеристики, основной из которых является закон распределения.

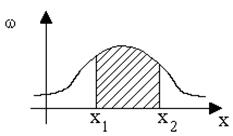
Закон распределения для непрерывных случайных функций задается в виде плотности вероятности w(x), называемой дифференциальным законом распределения (рис.9.3).

Рис. 9.3. Дифференциальный закон распределения

Выражение w(x)dx означает вероятность того, что случайная величина содержится между x и x+dx:

. (9.1)

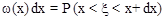
Вероятность того, что случайная величина содержится между значениями x₁ и x₂, определяется формулой

, (9.2)

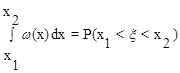
что геометрически выражается заштрихованной площадью на рис.9.3.

Вся площадь под кривой w(x) равна единице:

. (9.3)

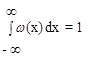
Хотя закон распределения полностью определяет случайную величину, на практике используются более простые усредненные статистические характеристики случайной величины, выражающиеся в виде обыкновенных неслучайных чисел.

Статистический метод изучает не отдельную реализацию случайного процесса, а свойство всего множества в целом путем их усреднения. При этом используются следующие статистические характеристики.

Среднее по множеству значение случайной величины (математи-ческое ожидание)

. (9.4)

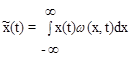
Среднее по множеству значение квадрата случайной величины

. (9.5)

, (9.6)

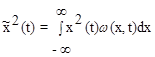
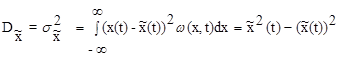
где 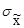— среднеквадратичное отклонение.

Для стационарных случайных процессов эти характеристики не зависят от времени t, в отличие от нестационарных случайных процессов.

Среднее значение случайного процесса представляет собой некоторую среднюю кривую, около которой группируются все возможные отдельные реализации этого процесса, а дисперсия или среднеквадратичное отклонение характеризуют рассеяние отдельных возможных реализаций процесса около этой средней кривой.

Кроме средних по множеству значений случайной величины определяют средние по времени значения для отдельной реализации случайного процесса.

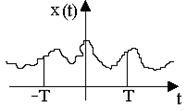
Среднее значение по времени случайной величины x определяется на интервале времени T (рис.9.4)

. (9.7)

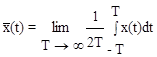
Рис. 9.4. Реализации случайного процесса

Среднее значение по времени квадрата случайной функции x

. (9.8)

, (9.9)

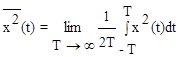
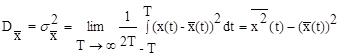
где 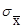— среднеквадратичное отклонение.

Стационарные случайные процессы обладают свойством эргодической гипотезы, в соответствии с которой для стационарного случайного процесса с вероятностью, равной единице, всякое среднее по множеству равно соответствующему среднему по времени, в частности

(9.10)

Эргодическая гипотеза позволяет значительно упростить все расчеты и эксперименты. Она позволяет для определения статистических характеристик, вместо параллельного испытания многих однотипных систем в один и тот же момент времени, пользоваться одной кривой x(t), полученной при испытании одной системы в течение длительного времени.

Таким образом, важное свойство стационарного случайного процесса состоит в том, что отдельная его реализация на бесконечном промежутке времени полностью определяет собой весь случайный процесс со всеми бесчисленными возможными его реализациями.

Корреляционная функция. Начальный корреляционный момент двух значений случайной функции x(t) и x(t₁), взятых в моменты времени t и t₁, носит название корреляционной (автокорреляционной) функции. Корреляционная функция является универсальной характеристикой для случайного процесса. Она определяет зависимость случайной величины в последующий момент времени x(t₁) от предыдущего значения x(t) в момент времени t. Это есть мера связи между ними.

В случае стационарного случайного процесса (рис.9.5) корреляционная функция R(t) представляет собой среднее во времени значение за промежуток времени T®¥ от произведения случайных величин x(t) и x(t+t), взятых в случайном процессе в любые два момента времени, отличающихся друг от друга на определенный промежуток времени t

. (9.11)

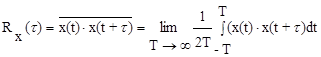
Рис. 9.5. Реализации случайного процесса

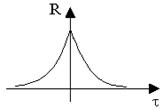
Для стационарного случайного процесса корреляционная функция определяет зависимость случайной величины x в последующий момент времени t+t от предыдущего значения в момент t. Корреляционная функция имеет вид, представленный на рис.9.6. Чем менее инерционен объект наблюдения, тем быстрее убывает R(t) с увеличением t. Она постоянна для всех случайных процессов, подчиненных одинаковому закону распределения.

Рис. 9.6. Корреляционная функция случайного процесса

Основные свойства корреляционной функции стационарного случайного процесса [1].

Корреляционная функция является четной функцией, т.е. R(t)=R(-t).

При t=0 корреляционная функция дает средний квадрат случайной величины:

. (9.12)

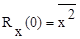
R(¥) = 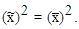(9.13)

Корреляционная функция суммы двух стационарных случайных процессов z(t)=x(t)+y(t) определяется как

, (9.14)

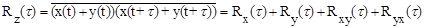
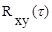
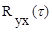
где , — взаимные корреляционные функции.

Они характеризуют взаимную связь двух случайных процессов между собой в разные моменты времени, отстоящие друг от друга на промежуток времени t. При t=0 будет = .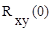

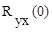
Спектральная плотность стационарного случайного процесса.

Представляет собой прямое преобразование Фурье от корреляционной функции

. (9.15)

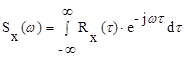
Чтобы определить корреляционную функцию R_x(t) по известной спектральной плотности S_x(w) используется обратное преобразование Фурье

. (9.16)

. 9.17)

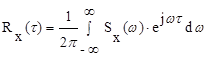
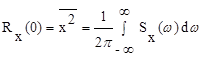
По своему физическому смыслу спектральная плотность есть величина, которая пропорциональна средней мощности процесса в интервале частот от w до w+dw.

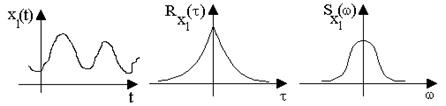
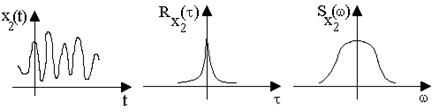
Рис. 9.7. Взаимосвязь между случайной функцией и ее характеристиками

Аналогично взаимным корреляционным функциям введено понятие взаимных спектральных плотностей:

; (9.18)

. (9.19)

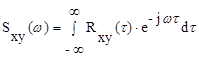
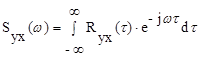
Связь между случайной функцией, ее корреляционной функцией и спектральной плотностью приведена на рис.9.7.

Источник