Что такое случайный сигнал
Случайный сигнал
Случайные сигналы — сигналы, мгновенные значения которых (в отличие от детерминированных сигналов) не известны, а могут быть лишь предсказаны с некоторой вероятностью, меньшей единицы. Характеристики таких сигналов являются статистическими, то есть имеют вероятностный вид. Существует 2 основных класса случайных сигналов. Во-первых, это шумы — хаотически изменяющиеся во времени электромагнитные колебания, возникающие в разнообразных физических системах из-за беспорядочного движения носителей заряда. Во-вторых, случайными являются все сигналы, несущие информацию, поэтому для описания закономерностей, присущих осмысленным сообщениям, также прибегают к вероятностным моделям.
Случайный процесс (СП). Реализация СП
Математическая модель изменяющегося во времени случайного сигнала называется случайным процессом. По определению, случайный процесс X(t) это функция особого вида, характеризующаяся тем, что значения, принимаемые ею в любой момент времени t, являются случайными величинами. До регистрации (до приёма) случайный сигнал следует рассматривать именно как случайный процесс, представляющий собой совокупность (ансамбль) функций времени Xj(t), подчиняющихся некоторой общей для них статистической закономерности. Одна из этих функций, ставшая полностью известной после приёма сообщения, называется реализацией случайного процесса. Эта реализация является уже не случайной, а детерминированной функцией времени. Для анализа свойств и характеристик случайного процесса, а также различных его преобразований, необходимо задать математическую модель случайного процесса. Такая модель может представлять собой описание возможных реализаций случайного процесса в сочетании с указанием относительной частоты их появления.
Пример
В качестве примера рассмотрим гармонический сигнал со случайной начальной фазой. Во многих практических задачах используется модель случайного процесса, реализации которого представляют собой гармонические колебания с известными (детерминированными) амплитудой и частотой, но случайной начальной фазой. Таким образом, реализация рассматриваемого случайного процесса может быть записана как: x(t)=A*cos(
*t+φ), где А амплитуда (детерминированная), — частота (детерминированная), и φ — случайная начальная фаза, которая в большинстве практически интересных случаев может считаться равномерно распределённой на интервале 0…2π, то есть имеющей следующую плотность вероятности:
Графики нескольких реализаций данного случайного процесса, представляющие собой смещённые друг относительно друга по временной оси синусоиды, показаны на рис. Как видим, конкретный вид реализации процесса в данном случае определяется значением всего лишь одной случайной величины: начальной фазы. Случайные процессы, конкретный вид реализаций которых определяется значениями конечного числа параметров (случайных величин), называют квазидетерминированными случайными процессами.
Литература
Теоретические основы радиотехники: Учеб. Пособие. М. Т. Иванов, А. Б. Сергиенко, В. Н. Ушаков; Под ред. В. Н. Ушакова. М.: Высш. шк., 2002.
Детерминированный и Случайный сигналы
Шумом называются нежелательные явления мешающие получать информацию из полезного сигнала. Шум присутствует повсюду, он случаен по своей природе, источниками его может быть как физика самого процесса, который можно зафиксировать, так и неидеальности приемной аппаратуры или оцифровщиков. Нужно различать понятия шумов и полезного сигнала, в том числе и с точки зрения их математического описания.
Детерминированные и случайные сигналы
Давайте рассмотрим, как можно описать полезный сигнал. В качестве математической модели используем детерминированный сигнал заданный аналитической функцией.
Значение сигнала можно определить в любой момент времени, подставив все необходимые аргументы в описывающую его аналитическую функцию. На примере представлены синусоиды, если зафиксировать параметры амплитуды, частоты и фазы, и передавать в формуле меняющееся значение времени, будем получать точное значение сигнала в эти моменты времени.
Детерминированный сигнал
Детерминированный сигнал описываемой аналитической функции, как модель очень удобен, но сигналы реального мира подвержены воздействию множества физических факторов. Их значения могут колебаться от наблюдения к наблюдению, да и сами средства наблюдения также могут вносить погрешность измерений. Проще говоря, реальный сигнал будет отличаться от его аналитического описания на случайную величину ошибки.
Рассмотрим очередной бытовой пример, нагрев воды в чайнике на газовой горелке. Температура воды с течением времени монотонно нарастает, но мы наблюдаем некоторые флуктуации или отклонения. Это может быть обусловлено неравномерной подачей газа в горелке, ветром, термодинамикой, неидеальностью средств измерения, так или иначе полученные отсчеты мы можем приблизить прямой линией.
Прямая линия это детерминированный сигнал описываемой функции. Можно узнать его значение между соседними отчетами, то есть интерполировать данные эксперименты или даже подсчитать величину сигнала за пределами периода наблюдения, то есть использовать его для прогнозирования значений температуры.
Но реальные значения немного отличаются от линейной зависимости в большую или меньшую сторону. Записанный сигнал можно рассматривать, как математическую модель типа детерминированный сигнал плюс случайный процесс. Если с детерминированным описанием сигналов все более менее понятно, то с моделью случайного процесса нам только предстоит познакомиться.
Случайный процесс
Понятие случайного процесса связано с определением случайной функции. Случайная функция это функция, вид который в результате проведения эксперимента мы не можем предугадать. Случайный процесс — случайная функция времени. Конкретный вид результата протекания случайного процесса называется реализацией. На рисунке ниже показан ансамбль реализации одного случайного процесса.
В отличии от сигналов описываемых аналитической функцией, реализация случайного процесса, практически всегда отличаются друг от друга, но общие характеристики у них есть. Как же нам описать случайный процесс без необходимости хранения бесконечного числа его реализаций? Для описания мы используем теорию вероятностей и математическую статистику.
Распределение случайной величины
Простой пример дискретной случайной величины, число выпадающие при броске игральных костей, может выпасть значение от 1 до 6. Величина может принимать одно из шести дискретных значений, но совершенно случайно. Не трудно подсчитать вероятность выпадения какого-либо числа, она равна 1/6 или 16,67% для каждого из дискретных значений.
Рассмотрим пример непрерывной случайной величины. Рост человека, он не изменяется дискретно, может принимать любое значение в разумных пределах. Представим себе, что мы измеряем рост каждого посетителя, кто заходит в магазин. Измерив достаточное количество людей можно построить вот такой график, по оси x отложен рост в сантиметрах, по оси y количество людей с таким ростом.
На графике мы видим дискретные полоски, но эти полоски обозначают количество людей чей рост попадает в определенной пределы. Например, в пределы от 182 до 183 сантиметров. Взглянув на этот график выше, мы понимаем, что чаще всего в магазин заходили люди среднего роста, а посетителей ростом выше двух метров видели редко. То, что было представлено на графике очень близко к понятию плотности распределения случайной величины.
Плотность распределения
Значение плотности распределения показывает вероятность того, что случайная величина примет определенное значение, а частичная площадь под графиком вероятность того, что значение попадет в выбранный предел.
Как вы понимаете, площадь под графиком на всем диапазоне значений равна единице или 100 %. В случае с игральными костями, мы рассматривали равномерное распределение, то есть одинаковую вероятность того, что случайная величина примет, то или иное значение.
В случае с ростом человека, мы наблюдали нормальное распределение, также именуемое распределением Гаусса. Нормальное распределение широко распространено в природе и используется как удобная модель случайного процесса. Популярность эта вытекает из центральной предельной теоремы, она гласит что сумма большого количества слабо зависимых случайных величин имеет распределение, близкое к нормальному. На отклонение величины от среднего влияет множество факторов, подобно тому, как множество факторов влияет на рост человека, поэтому сумму их влияний можно описать случайным процессом с Гауссовским или Нормальным распределением.
Убедимся в этом в matlab. Смотри с 05:00 минуты!
Плотность распределения это лишь одна из характеристик которыми мы описываем случайные процессы.
Характеристики случайных сигналов
Поскольку все информационные сигналы и помехи являются случайными и могут быть предсказаны лишь с некоторой степенью вероятности, то для описания таких сигналов используется теория вероятностей. При этом используются статистические характеристики, которые получают путем проведения многочисленных опытов в одинаковых условиях.
Все случайные явления, изучаемые теорией вероятностей можно разделить на три группы:
— случайные события;
— случайные величины;
— случайные процессы.
Случайное событие — это всякий факт, который в результате опыта может произойти или не произойти.
Случайным событием является появление помехи на входе приемника или прием сообщения с ошибкой.
Случайные события обозначаются латинскими буквами А, В, С.
Числовыми характеристиками случайного события являются:
1. Частота появления случайного события:
где m — количество опытов, в которых произошло данное событие;
N — общее количество проведенных опытов.
Как следует из выражения (40) частота появления случайного события не может превышать 1, т. к. количество опытов, в которых произошло данное событие не может привысить общее количество проведенных опытов.
2. Вероятность появления случайного события:
Т. е. вероятность появления случайного события есть частота его появления при неограниченном увеличении количества проведенных опытов. Вероятность появления события не может превышать 1. Случайное событие, имеющее вероятность равную единице является достоверным, т. е. оно обязательно произойдет, поэтому такую вероятность имеют уже произошедшие события.
Случайная величина — это величина, которая от опыта к опыту изменяется случайным образом.
Случайной величиной является амплитуда помехи на входе приемника или количество ошибок в принятом сообщении. Случайные величины обозначаются латинскими буквами X, Y, Z, а их значения — x, y, z.
Случайные величины бывают дискретными и непрерывными.
Дискретной называется случайная величина, которая может принимать конечное множество значений (например, количество оборудования, количество телеграмм и т. д., т. к. они могут принимать только целое число 1, 2, 3, …).
Непрерывной называется случайная величина, которая может принимать любые значения из некоторого диапазона (например, амплитуда помехи на входе приемника может принимать любые значения, точно так же как и любые значения может принимать информационный аналоговый сигнал).
Числовыми, статистическими характеристиками, описывающими случайные величины являются:
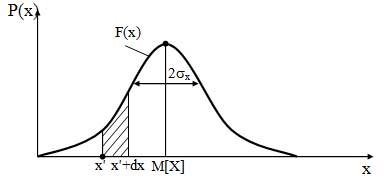
1. Функция распределения вероятности.
Данная характеристика показывает вероятность попадания значения случайной величины в малый интервал dx в окрестности точки х’, т. е. в заштрихованную область (рисунок).
3. Математическое ожидание.
где хi — значения случайной величины;
Р(хi) — вероятность появления этих значений;
n — количество возможных значений случайной величины.
где р(х) — плотность вероятности непрерывной случайной величины.
По своему смыслу математическое ожидание показывает среднее и наиболее вероятное значение случайной величины, т. е. это значение наиболее часто принимает случайная величина. Выражение (44) применяется, если случайная величина является дискретной, а выражение (45), если она является непрерывной. Обозначение M[X] является специальным для математического ожидания того случайной величины, которая указана в квадратных скобках, однако иногда используются обозначения mх или m.
4. Дисперсия.
Все характеристики случайной величины можно показать с помощью рисунка 22.
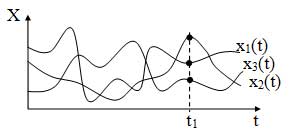
Случайный процесс — это такая функция времени t, значение которой при любом фиксированном значении времени является случайной величиной. Например, на рисунке 23 показана диаграмма некоторого случайного процесса, наблюдаемого в результате проведения трех опытов. Если определить значение функций в фиксированный момент времени t1, то полученные значения окажутся случайными величинами.
Таким образом, наблюдение любой случайной величины (Х) во времени, является случайным процессом Х(t). Например, как случайные процессы, рассматриваются информационные сигналы (телефонные, телеграфные, передачи данных, телевизионные) и шумы (узкополосные и широкополосные).
Однократное наблюдение случайного процесса называется реализацией xk(t). Совокупность всех возможных реализаций одного случайного процесса называется ансамблем реализаций. Например, на рисунке 23 представлен ансамбль реализаций случайного процесса, состоящий из трех реализаций.
Для характеристики случайных процессов используются те же характеристики, что и для случайных величин: функция распределения вероятности, плотность распределения вероятности, математическое ожидание и дисперсия. Данные характеристики рассчитываются аналогично, как и для случайных величин. Случайные процессы бывают различных типов. Однако в электросвязи большинство случайных сигналов и помех относятся к стационарным эргодическим случайным процессам.
Стационарным является случайный процесс, у которого характеристики F(x), P(x), M[X] и D[X] не зависят от времени.
Эргодическим является процесс, у которого усреднение по времени одной из реализации приводит к тем же результатам, что и статическое усреднение по всем реализациям. Физически это означает, что все реализации эргодического процесса похожи друг на друга, поэтому измерения и расчеты характеристик такого процесса можно проводить по одной (любой) из реализаций.
Кроме четырех характеристик приведенных выше случайные процессы также описываются функцией корреляции и спектральной плотностью мощности.
где tн — время наблюдения реализации xk(t).
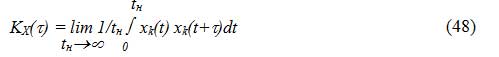
Спектральная плотность мощности — показывает распределение мощности случайного процесса по частотам.
Таким образом, наблюдение случайного явления во времени является случайным процессом, его появление является случайным событием, а его значение случайной величиной.
Например, наблюдение телеграфного сигнала на выходе линии связи в течение, какого то времени — это случайный процесс, появление на приеме его дискретного элемента «1» или «0» — случайное событие, а амплитуда этого элемента — случайная величина.
Случайный сигнал
Существует 2 основных класса случайных сигналов. Во-первых, это шумы — беспорядочные колебания различной физической природы, отличающиеся сложностью временной и спектральной структуры. Во-вторых, случайными являются все сигналы, несущие информацию, которые для описания закономерностей, присущих осмысленным сообщениям, также прибегают к вероятностным моделям.
Связанные понятия
В статистике под латентными или скрытыми переменными понимают такие переменные, которые не могут быть измерены в явном виде, а могут быть только выведены через математические модели с использованием наблюдаемых переменных. Скрытые переменные используются во многих областях, включая психологию, экономику, машинное обучение, биоинформатику, обработку естественного языка и социальные науки.
Модели дискретного выбора — экономические (эконометрические) модели, позволяющие описывать, объяснять и прогнозировать выбор между, двумя или более альтернативами (то есть когда множество альтернатив не более чем счетно). Модели дискретного выбора позволяют на основе некоторых характеристик (атрибутов) экономического субъекта или ситуации оценить вероятность выбора той или иной альтернативы.
В физике и математике, в отрасли динамических систем, двойной маятник — это маятник с другим маятником, прикреплённым к его концу. Двойной маятник является простой физической системой, которая проявляет разнообразное динамическое поведение со значительной зависимостью от начальных условий. Движение маятника руководствуется связанными обыкновенными дифференциальными уравнениями. Для некоторых энергий его движение является хаотическим.
В обработке сигналов чирплет-преобразование — это скалярное произведение входного сигнала с семейством элементарных математических функций, именуемых чирплетами.
В статистике метод оценки с помощью апостериорного максимума (MAP) тесно связан с методом максимального правдоподобия (ML), но дополнительно при оптимизации использует априорное распределение величины, которую оценивает.
В гармоническом приближении колебания атомов решётки вокруг равновесного положения представляют как набор квазичастиц, называемых фононами. Они имеют целый спин и соответственно являются бозонами. Знание фононного спектра (зависимость энергии фонона от волнового вектора) позволяет определять коэффициенты теплопроводности, скорости звука, фононные теплоёмкости, рамановские спектры и другие параметры кристаллов.
Случайный сигнал
Сигнал, мгновенные значения которого являются случайными величинами.
Примечание. Случайный сигнал, любая вероятная характеристика которого, полученная усреднением по множеству возможных реализаций с вероятностью, сколь угодно близкой к единице, равна временному среднему, полученному усреднением за достаточно большой промежуток времени одной реализации, называется эргодическим. Рассмотренные выше характеристики случайного сигнала определены для эргодического сигнала
Смотреть что такое «Случайный сигнал» в других словарях:
случайный сигнал — Сигнал, мгновенные значения которого являются случайными величинами. Примечание Случайный сигнал, любая вероятная характеристика которого, полученная усреднением по множеству возможных реализаций с вероятностью, сколь угодно близкой к единице,… … Справочник технического переводчика
Случайный сигнал — Случайные сигналы сигналы, мгновенные значения которых (в отличие от детерминированных сигналов) не известны, а могут быть лишь предсказаны с некоторой вероятностью, меньшей единицы. Характеристики таких сигналов являются статистическими, то есть … Википедия
случайный сигнал — atsitiktinis signalas statusas T sritis fizika atitikmenys: angl. random signal vok. Zufallssignal, n rus. случайный сигнал, m pranc. signal aléatoire, m … Fizikos terminų žodynas
Случайный сигнал — 1. Сигнал, мгновенные значения которого являются случайными величинами Употребляется в документе: Приложение № 6 ГОСТ 16465 70 Сигналы радиотехнические измерительные. Термины и определения … Телекоммуникационный словарь
Стационарный случайный сигнал — 8. Стационарный случайный сигнал Случайный сигнал, у которого плотность вероятности любой совокупности мгновенных значений не изменяется при любом сдвиге этой совокупности во времени. Примечание. Случайный сигнал, у которого среднее значение и… … Словарь-справочник терминов нормативно-технической документации
нестационарный случайный сигнал — Случайный сигнал, у которого плотность вероятности некоторой совокупности мгновенных значений изменяется при некотором сдвиге этой совокупности во времени. [ГОСТ 16465 70] Тематики телевидение, радиовещание, видео Обобщающие термины классификация … Справочник технического переводчика
Нестационарный случайный сигнал — 1. Случайный сигнал, у которого плотность вероятности некоторой совокупности мгновенных значений изменяется при некотором сдвиге этой совокупности во времени Употребляется в документе: Приложение № 6 ГОСТ 16465 70 Сигналы радиотехнические… … Телекоммуникационный словарь
Стационарный случайный сигнал — 1. Случайный сигнал, у которого плотность вероятности любой совокупности мгновенных значений не изменяется при любом сдвиге этой совокупности во времени Употребляется в документе: Приложение № 6 ГОСТ 16465 70 Сигналы радиотехнические… … Телекоммуникационный словарь
Сигнал (техника) — Сигнал в теории информации и связи называется материальный носитель информации, используемый для передачи сообщений по системе связи. Сигналом может быть любой физический процесс, параметры которого изменяются в соответствии с передаваемым… … Википедия