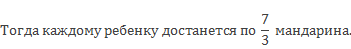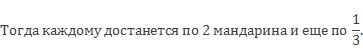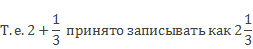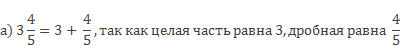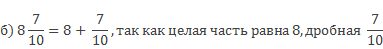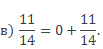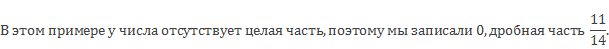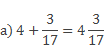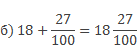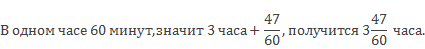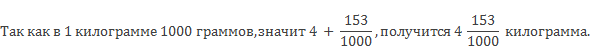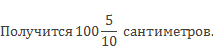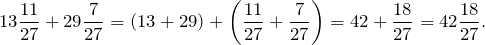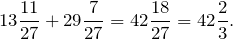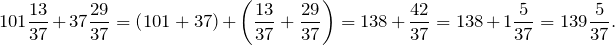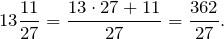Что такое смешное число
Смешанные числа, перевод смешанного числа в неправильную дробь и обратно
В этом материале мы разберем такое понятие, как смешанные числа. Начнем, как всегда, с определения и небольших примеров, потом поясним связь смешанных чисел и неправильных дробей. После этого мы изучим, как правильно выделять целую часть из дроби и получать в результате целое число.
Понятие смешанного числа
Числа вида 0 3 14 также не относятся к смешанным. Здесь не выполняется первая часть условия: целая часть должна быть представлена только натуральным числом, а нуль им не является.
Как соотносятся между собой неправильные дроби и смешанные числа
Эту связь проще всего проследить на конкретном примере.
Наш пример доказывает, что в виде смешанного числа можно представить любую неправильную дробь.
Мы поняли, как приводить неправильную дробь к виду смешанного числа. Если в числителе неправильной дроби стоит такое число, которое можно разделить на знаменатель без остатка, то можно сделать это, и тогда наша неправильная дробь станет натуральным числом.
Как перевести смешанное число в неправильную дробь
Чтобы успешно решать задачи, полезно уметь производить и обратное действие, то есть делать из смешанных чисел неправильные дроби. В этом пункте мы разберем, как правильно это сделать.
Для этого нужно воспроизвести следующую последовательность действий:
1. Для начала представляем имеющееся смешанное число n a b как сумму целой и дробной части. Получается n + a b
2. Далее заменяем целую часть на дробь со знаменателем, равным единице (то есть записываем n как n 1 ).
Разберем это действие на конкретном примере.
Представьте 5 3 7 в виде неправильной дроби.
Решение
Последний шаг – сложение дробей, имеющих разные знаменатели:
5 1 + 3 7 = 35 7 + 3 7 = 38 7
Представьте 15 2 5 в виде неправильной дроби.
Решение
Как выделить из неправильной дроби целую часть
Обычно мы не указываем неправильную дробь в качестве итогового ответа. Принято доводить вычисления до конца и заменять ее либо натуральным числом (разделив числитель на знаменатель), либо смешанным числом. Как правило, первый способ используется, когда разделить числитель на знаменатель можно без остатка, а второй – если такое действие невозможно.
Когда мы выделяем из неправильной дроби целую часть, мы просто заменяем ее равным смешанным числом.
Разберем, как именно это делается.
Приведем доказательство этого утверждения.
Выделение целой части из неправильной дроби a b осуществляется таким образом:
1) производим деление a на b с остатком и записываем неполное частное q и остаток r отдельно.
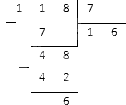
Представьте 107 4 в виде смешанного числа.
Решение
Делим 104 на 7 столбиком:
Нам осталось посмотреть, как заменить неправильную дробь натуральным числом (при условии, что ее числитель делится на знаменатель без остатка).
Смешанные числа

Всего получено оценок: 97.
Всего получено оценок: 97.
Большая часть смешанных чисел достаточно громоздки в записи, поэтому их редко используют для составления задач. Но ученики 5 класса впадают в ужас при виде монструозных примеров со смешанными числами. Поэтому рассмотрим тему в отдельности, чтобы не допускать ошибок в дальнейшем.
Что такое смешанная дробь?
Смешанная дробь это дробь, у которой есть две части: целая и дробная. При этом дробная часть обязательно не должна равняться нулю.
Целая часть, равная нулю, есть у любой обыкновенной дроби.
Всего существует 4 вида дробей:
Смешанная дробь может быть записана в десятичном виде, так же, как и обыкновенная. А вот неправильную дробь в строку записать невозможно. И главное, нельзя забывать, что смешанные дроби и смешанные числа это одно и то же.
Откуда появляются смешанные дроби?
Вариантов возникновения в задаче смешанных дробей всего 2:
Зачем нужны смешанные числа?
Помимо записи результатов, смешанные числа очень часто применяются в примерах с десятичными дробями. Ни один отсчет, исследование или расчеты не обходятся без применения десятичных дробей. А довольствоваться только дробями от минус бесконечности до 0 невозможно. Поэтому и применяют смешанные числа в расчетах. При этом отдельного правила смешанных чисел нет.
Что мы узнали?
Мы вспомнили, какие бывают дроби. Поговорили о каждой из них в отдельности. Выделили смешанные числа. Рассказали, откуда смешанные числа могут появиться в задачах и как правильно записывать ответы дробных примеров. Пояснили, для чего нужны смешанные числа в современном мире.
Что такое смешное число
Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту
В этом уроке Вы познакомитесь с понятием смешанного числа и научитесь решать различные задания с использованием смешанных чисел.
Давайте решим такую задачу:
Надо разделить 7 мандаринов на троих ребят поровну. Сколько достанется каждому?
Например, можно разделить каждый мандарин на три равные части.
А можно при делении 7 мандаринов каждому ребенку сначала дать по 2 целых мандарина, а потом оставшийся один мандарин разделить на три части.
Смешанное, потому что присутствуют две части: целая и дробная. Число 2 называют целой частью числа 2 целых 1/3, а число 1/3 называют его дробной частью.
Таким образом, получили следующее определение:
Запись числа, содержащую целую и дробную части, называют смешанной.
Для краткости вместо «Число в смешанной записи» говорят смешанное число. Смешанное число можно представить и в виде неправильной дроби, но об этом Вы узнаете позже.
Давайте выполним несколько заданий.
Представьте число в виде суммы его целой и дробной частей:
Запишите в виде смешанного числа сумму:
Смешанные числа применяют, например, при выражении величин.
Выразите в часах 3 часа 47 минут.
Выразите в килограммах 4 килограмма 153 грамма.
Выразите в сантиметрах 1 метр 5 миллиметров.
Что такое смешанные числа
Доброго времени суток!
Что такое смешанные числа? Как над ними выполнять арифметические действия? Кто может объяснить на простеньких примерах.
Спасибо за участие!
Смешанным числом называют число, которое в своей записи содержит натуральное число (целая часть) и простую дробь (дробная часть).
Например, числа 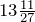
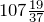
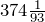
Над смешанными числами выполняют арифметические действия.
Например, для сложения смешанных чисел необходимо отдельно сложить их целые части и дробные части.
Пример.
Сложим смешанные числа 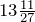
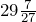
Решение.
Обратим внимание, что дробь 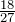
Ответ. 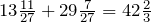
Рассмотрим пример, когда при сложении дробных частей получим неправильную дробь. В таком случае нужно выделить целую часть и добавить ее к целой части, полученной при сложении смешанных чисел.
Пример.
Сложим числа 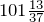
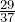
Решение.
Ответ. 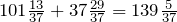
Часто для выполнения арифметических действий со смешанными числами их нужно перевести в неправильную дробь, а затем выполняют действия как над рациональными числами.
Чтобы выполнить перевод смешанного числа в неправильную дробь, нужно знаменатель дроби умножить на целую часть смешанного числа и добавить к числителю дроби. Знаменатель оставляют без изменений.
Пример.
Переведем число 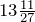
Решение.
Ответ. 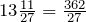
Урок 38 Бесплатно Смешанные числа
На данном уроке мы продолжим разговор об обыкновенных дробях.
Выясним, какие числа называют смешанными, как их принято записывать и читать.
Установим связь между смешанными числами и правильными дробями.
Научимся переводить смешанное число в неправильную дробь.
Рассмотрим обратную операцию перевода неправильной дроби в смешанное число.
Определим расположение смешанных чисел на координатном луче.
Взаимосвязь между смешанным числом и неправильной дробью
Правильной называют дробь, в которой числитель меньше знаменателя, она всегда меньше единицы.
Неправильной называют дробь, в которой числитель больше знаменателя или равен ему, такие дроби всегда больше единицы.
Сегодня речь пойдет о неправильных дробях.
Рассмотрим несколько примеров.
Пример №1.
Разделили три конфеты на троих человек.
Сколько конфет получил каждый?
Известно, что обыкновенная дробь \(\mathbf<\frac
Общее количество конфет (m = 3) разделим на количество человек (n = 3).
Запишем частное в виде дроби.
В результате получили неправильную дробь, в которой числитель равен знаменателю.
\(\mathbf<\frac<3> <3>= 3 \div 3 = 1>\) (конф.) получил каждый.
Ответ: каждый получил 1 конфету.
Пример №2.
Разделили поровну шесть конфет между тремя друзьями.
Сколько конфет получил каждый?
Общее количество конфет (m = 6) разделим на количество друзей (n = 3).
Запишем частное в виде дроби.
В итоге получилась неправильная дробь, в которой числитель больше знаменателя.
\(\mathbf<\frac<6> <3>= 6 \div 3 = 2>\) (конф.) получил каждый из друзей.
Ответ: по 2 конфеты получил каждый из друзей.
В рассмотренных примерах частное двух чисел найти было нетрудно, так как числитель дроби нацело делится на знаменатель.
Рассмотрим еще одну ситуацию.
Пример №3.
Два брата решили разделить поровну пять апельсинов.
Сколько апельсинов достанется каждому из братьев?
Общее количество апельсинов (m = 5) разделим на количество братьев (n = 2).
Запишем частное в виде дроби.
В данном примере мы получили неправильную дробь, в которой числитель хоть и больше знаменателя, но он не делится нацело.
Разделить пять апельсинов на две равные части можно двумя способами.
1. Можно разрезать каждый апельсин на две равные части.
Каждая полученная часть будет равна ½ апельсина.
Тогда по одной части от каждого апельсина достанется каждому из братьев.
Оба мальчика получат по пять таких частей: \(\mathbf<\frac<1> <2>+ \frac<1> <2>+ \frac<1> <2>+ \frac<1> <2>+ \frac<1><2>>\)
Следовательно, каждый получит \(\mathbf<\frac<5><2>>\) апельсина.
Если внимательно присмотреться к сумме дробей, можно заметить, что две части, т.е. сумма \(\mathbf<\frac<1> <2>+ \frac<1><2>>\) составляет \(\mathbf<\frac<2><2>>\).
В свою очередь нам известно, что неправильная дробь \(\mathbf<\frac<2><2>>\) равна единице: \(\mathbf<\frac<2> <2>= 2 \div 2 = 1>\).
Таким образом получится, что каждому мальчику достанется два апельсина, да еще половинка: \(\mathbf<2 + \frac<1><2>>\) апельсина.
2. Можно поделить поровну сначала целые апельсины.
В таком случае каждому брату достанется по два апельсина.
Затем оставшийся апельсин необходимо разделить поровну на двоих, так каждый получит еще по половине апельсина, т.е. (\(\mathbf<\frac<1><2>>\)) его часть.
В результате оба брата получат по два целых апельсина, да еще половину: \(\mathbf<2 + \frac<1><2>>\) апельсина.
Сумму \(\mathbf
Такую сокращенную запись называют смешанным числом, оно имеет целую часть (натуральное число) и дробную часть (дробное число).
Дробная часть смешанного числа- это всегда правильная дробь.
Например, представим смешанные числа в виде суммы их целой и дробной части.
\(\mathbf<1\frac<4> <11>= 1 + \frac<4><11>>\) (целая часть равна 1, дробная- \(\mathbf<\frac<4><11>>\)).
\(\mathbf<7\frac<10> <15>= 7 + \frac<10><15>>\) (целая часть равна 7, дробная- \(\mathbf<\frac<10><15>>\)).
\(\mathbf<\frac<5> <16>= 0 + \frac<5><16>>\) (целая часть отсутствует, т.е. равна 0, дробная- \(\mathbf<\frac<5><16>>\)).
А теперь наоборот сумму натурального числа и правильной дроби представим в виде смешанного числа.
Выразим в килограммах 3 килограмма 150 граммов.
Известно, что 1 кг = 1000 г.
Значит 150 г- это часть от килограмма, т.е. часть от 1000 г.
Чтобы узнать какую часть составляет 150 г от 1000 г, необходимо 150 разделить на 1000, получим \(\mathbf<\frac<150><1000>>\).
В итоге имеем 3 килограмма, да еще часть- \(\mathbf<\frac<150><1000>>\) килограмма, получаем \(\mathbf<3 + \frac<150><1000>>\).
Ответ: 3 килограмма 150 граммов- это \(\mathbf<3\frac<150><1000>>\) килограмма.
Число, содержащее целую часть (натуральное число) и дробную часть (правильную дробь), называют смешанным числом.
Читают смешанное число следующим образом: произносится сначала целая часть, затем дробная, в соответствии с правилами чтения дробных чисел.
В нашем примере про апельсины выражение \(\mathbf<2 + \frac<1><2>>\) можно записать как \(\mathbf<2\frac<1><2>>\).
Число 2— это целая часть смешанного числа, а число \(\mathbf<\frac<1><2>>\) его дробная часть.
Читается данное число так: «Две целых одна вторая».
Любое смешанное число можно перевести в неправильную дробь.
Выясним взаимосвязь смешанных чисел и неправильных дробей на примере.
Испекли три одинаковые пиццы.
От первой пиццы съели несколько кусочков, в результате от нее осталась часть, равная \(\mathbf<\frac<5><8>>\) всей пиццы.
По сути осталось несъеденными 2 (две) целых да еще \(\mathbf<\frac<5><8>>\) (пять восьмых) пиццы.
Если мы сложим эти два числа, то получим сумму \(\mathbf<2 + \frac<5><8>>\).
Выражение \(\mathbf<2 + \frac<5><8>>\) представляет собой ничто иное, как смешанное число \(\mathbf<2\frac<5><8>>\) (две целых пять восьмых).
Общее количество оставшейся пиццы мы можем определить иначе.
Возьмем так же три одинаковые пиццы и разрежем каждую на восемь равных частей.
Теперь вторую и третью пиццу мы можем представить в виде дроби \(\mathbf<\frac<8><8>>\), а остаток от первой запишем как \(\mathbf<\frac<5><8>>\).
В результате общее количество несъеденной пиццы будет выражаться суммой:
При этом ясно, что общее количество оставшейся пиццы, найденное первым способом и вторым, совпадают, значит \(\mathbf<2\frac<5> <8>= \frac<21><8>>\).
Запишем алгоритм перевода смешанного числа в неправильную дробь.
Чтобы представить смешанное число в виде неправильной дроби, необходимо:
1. Умножить целую часть смешанного числа на знаменатель его дробной части.
2. К полученному произведению прибавить числитель дробной части.
3. Записать полученный результат суммы в числитель новой дроби.
4. Знаменатель оставить без изменений.
У меня есть дополнительная информация к этой части урока!
В буквенном виде перевод смешанного числа в неправильную дробь можно записать следующим образом:
Пусть А— целя часть смешанного числа.
\(\mathbf<\frac
Рассмотрим несколько примеров.
Пример №1.
Представьте смешанное число \(\mathbf<6\frac<2><5>>\) в виде дроби.
1. Умножим целую часть смешанного числа (число 6) на знаменатель его дробной части (число 5), получим число 30.
6 • 5 = 30
2. К полученному произведению (число 30) прибавим числитель дробной части смешанного числа (число 2), получим число 32.
3. Запишем полученную сумму (число 32) в числитель новой дроби, а знаменатель останется прежним (число 5).
Получили неправильную дробь \(\mathbf<\frac<32><5>>\).
Пример №2.
Представьте смешанное число \(\mathbf<20\frac<1><3>>\) в виде дроби.
Умножим целую часть смешанного числа на знаменатель его дробной части, к полученному произведению прибавим числитель дробной части, запишем полученный результат суммы в числитель новой дроби, а знаменатель оставим без изменений.
Получили неправильную дробь \(\mathbf<\frac<61><3>>\).
Пример №3.
Представьте смешанное число \(\mathbf<3\frac<3><4>>\) в виде дроби.
Умножим целую часть смешанного числа на знаменатель его дробной части, к полученному произведению прибавим числитель дробной части, запишем полученный результат суммы в числитель новой дроби, а знаменатель оставим без изменений.
Получили неправильную дробь \(\mathbf<\frac<15><4>>\).
Возможна и обратная операция.
Неправильную дробь, в которой числитель нацело не делится на знаменатель, можно представить в виде смешанного числа.
Чтобы перейти от неправильной дроби к смешенному числу, необходимо выделить целую часть.
Выделить целую часть из неправильной дроби- это значит заменить неправильную дробь равным ей смешанным числом.
Для этого необходимо разделить с остатком числитель неправильной дроби на знаменатель.
При этом неполное частное будет являться целой частью, остаток- числителем, а делитель- знаменателем.
Знаменатель неправильной дроби всегда равен знаменателю дробной части смешенного числа.
Запишем алгоритм выделения целой части из неправильной дроби.
Чтобы перейти от неправильной дроби к смешанному числу, необходимо:
1. Разделить с остатком числитель неправильной дроби на ее знаменатель.
2. Неполное частное будет представлять собой целую часть смешанного числа.
3. Если остаток есть, то его необходимо записать в числитель дробной части смешанного числа, а делитель в знаменатель.
У меня есть дополнительная информация к этой части урока!
На примере рассмотрим перевод неправильной дроби в смешанное число.
Выделим целую часть из неправильной дроби \(\mathbf<\frac<37><8>>\).
Давайте выполним деление с остатком в столбик («деление уголком»).
Наибольшее число, которое меньше 37 и делится на 8— это 32.
32 разделим на делитель 8, получим 4-это неполное частное.
Вычтем из делимого числа 37 найденное наибольшее число 32, получим число 5— это остаток от деления.
По-другому деление с остатком можно записать так 37 ÷ 8 = 4 ( ост. 5 ).
В результате получим смешанное число \(\mathbf<4\frac<5><8>>\), в котором 4— целая часть, \(\mathbf<\frac<5><8>>\)- дробная часть.
Пройти тест и получить оценку можно после входа или регистрации
Смешанные числа на координатном луче
Выясним, где на координатном луче находятся смешанные числа.
1. Для того чтобы изобразить на координатном луче смешанное число, важно выбрать правильно длину единичного отрезка.
Единичный отрезок целесообразно устанавливать такой длины, чтобы было удобно его разделить на части, количество которых должно соответствовать числу, стоящему в знаменателе.
2. Далее от начала отсчета нужно отложить определенное количество равных частей, соответствующих числу, стоящему в числителе.
Рассмотрим поясняющий пример.
Отметим на координатном луче точку с координатой \(\mathbf<2\frac<2><3>>\).
\(\mathbf<2\frac<2><3>>\)— это смешанное число.
Данное смешанное число содержит правильную дробь со знаменателем 3.
Следовательно, единичный отрезок разобьем на три равные части, каждая такая часть (доля) будет равна \(\mathbf<\frac<1><3>>\) единичного отрезка.
Изобразим горизонтальный координатный луч, направленный вправо, с началом отсчета в точке О(0) и единичным отрезком ОЕ, равным 1 единице.
В таком случае одна часть (доля единичного отрезка) соответствует дроби \(\mathbf<\frac<1><3>>\), две части- это \(\mathbf<\frac<2><3>>\), три части- это 1.
Чтобы изобразить смешанное число \(\mathbf<2\frac<2><3>>\), отсчитываем от начала координат два целых единичных отрезка, а от третьего единичного отрезка возьмем только две его доли из трех.
Отметим точку на координатном луче, назовем ее точка А(\(\mathbf<2\frac<2><3>>\)).
Переведем смешанное число в неправильную дробь.
Определим расположение точки с координатой \(\mathbf<\frac<8><3>>\).
Дробь \(\mathbf<\frac<8><3>>\) означает восемь долей единичного отрезка ОЕ.
Отложим от начала координат восемь долей, каждая из которых равна \(\mathbf<\frac<1><3>>\) единичного отрезка.
Попадем в точку с координатой \(\mathbf<\frac<8><3>>\).
В этой же точке мы ранее отметили точку А(\(\mathbf<2\frac<2><3>>\)).
Смешанное число и соответствующая ему неправильная дробь, у которой числитель больше знаменателя, на координатном луче находятся всегда правее единицы и принадлежат они одной и той же точке координатного луча.
Определим расположение точек В(\(\mathbf<1\frac<2><3>>\)), С(\(\mathbf<2\frac<1><3>>\)), D(\(\mathbf<\frac<12><3>>\)) на координатном луче.
Изобразим горизонтальный координатный луч, направленный вправо, с началом отсчета в точке О(0) и единичным отрезком ОЕ, равным 1 единице.
Так как знаменатель каждой заданной дроби равен трем, то разобьем единичный отрезок ОЕ на три равные части, каждая часть будет равна \(\mathbf<\frac<1><3>>\) ОЕ.
1. Смешанное число \(\mathbf<1\frac<2><3>>\) представляет собой один целый единичный отрезок, да еще две части (доли) из трех от второго единичного отрезка.
Следовательно, точка В(\(\mathbf<1\frac<2><3>>\)) будет удалена вправо от начала координат на расстояние одного целого единичного отрезка, да еще двух отрезков, каждый из которых равен одной доле единичного отрезка.
В данную точку также мы можем попасть, если от начала координат вправо отсчитаем пять долей единичного отрезка- (\(\mathbf<\frac<5><3>>\))ОЕ.
Таким образом точка с координатой \(\mathbf<\frac<5><3>>\) и точка с координатой \(\mathbf<1\frac<2><3>>\) это одна и та же точка на координатном луче.
Отметим тот факт, что \(\mathbf<1\frac<2><3>>\) смешанное число и соответствующая ему неправильная дробь \(\mathbf<\frac<5><3>>\) больше единицы, и на координатном луче данные точки располагаются правее единицы (правее точки E(1)).
2. Выясним, где на координатном луче будет находиться точка С(\(\mathbf<2\frac<1><3>>\)).
Смешанное число \(\mathbf<2\frac<1><3>>\) представляет собой два целых единичных отрезка, да еще одну часть (долю) из трех от третьего единичного отрезка.
Отметим точку С(\(\mathbf<2\frac<1><3>>\)) на координатном луче, для этого отсчитаем вправо от начала координат два целых единичных отрезка и еще одну долю единичного отрезка, равную \(\mathbf<\frac<1><3>>\) ОЕ.
Так же в данную точку можно попасть, если от начала координат вправо отсчитать семь долей единичного отрезка- (\(\mathbf<\frac<7><3>>\))OE.
Точка с координатой \(\mathbf<\frac<7><3>>\) и точка с координатой \(\mathbf<2\frac<1><3>>\) это одна и та же точка на координатном луче.
Смешанное число \(\mathbf<2\frac<1><3>>\) и соответствующая ему неправильная дробь \(\mathbf<\frac<7><3>>\) больше единицы, на координатном луче данные точки располагается правее единицы (правее точки E(1)) и правее найденной нами точки В(\(\mathbf<1\frac<2><3>>\)).
3. Обозначим на координатном луче точку D с координатой \(\mathbf<\frac<12><3>>\).
\(\mathbf<\frac<12><3>>\)- неправильная дробь, в которой числитель больше знаменателя.
Найдем соответствующее этой дроби смешанное число, для этого выделим из дроби \(\mathbf<\frac<12><3>>\) целую часть.
Получается, что дробь \(\mathbf<\frac<12><3>>\) равна четырем целым единичным отрезкам.
Дробная часть данного числа отсутствует, т.е. она равна нулю.
\(\mathbf<\frac<12><3>>\) и 4— это одно и то же число, значит \(\mathbf<\frac<12> <3>= 4>\).
Отложим от начала координат четыре целых единичных отрезка и обозначим точку D(\(\mathbf<\frac<12><3>>\)).
Обратите внимание как расположены смешанные числа на координатном луче, чем правее от единицы находится смешанное число, тем оно больше.
Пройти тест и получить оценку можно после входа или регистрации