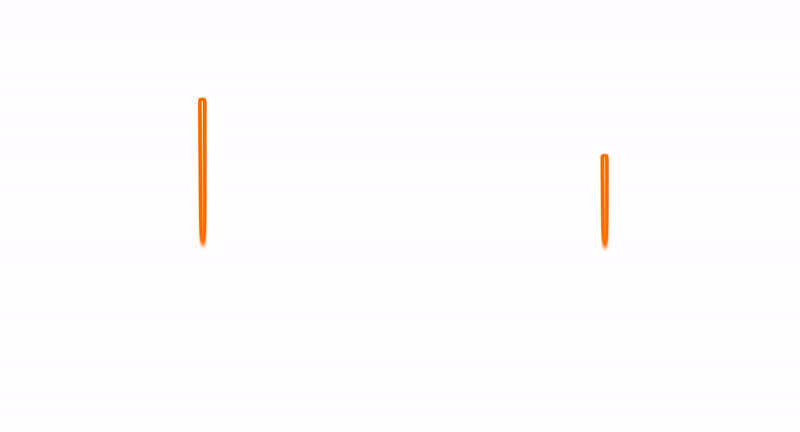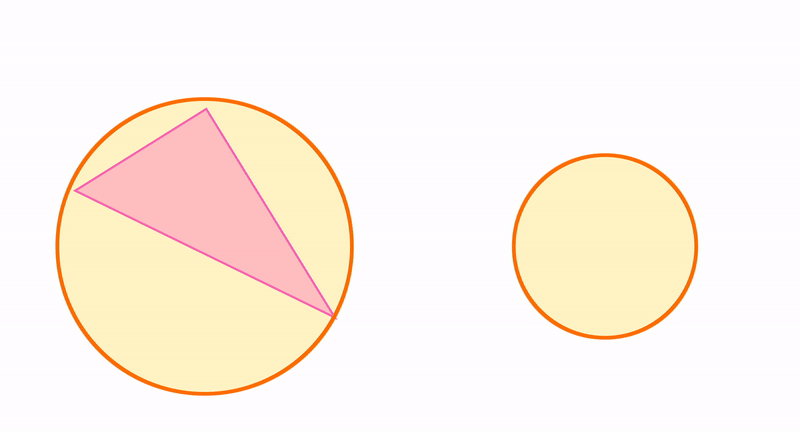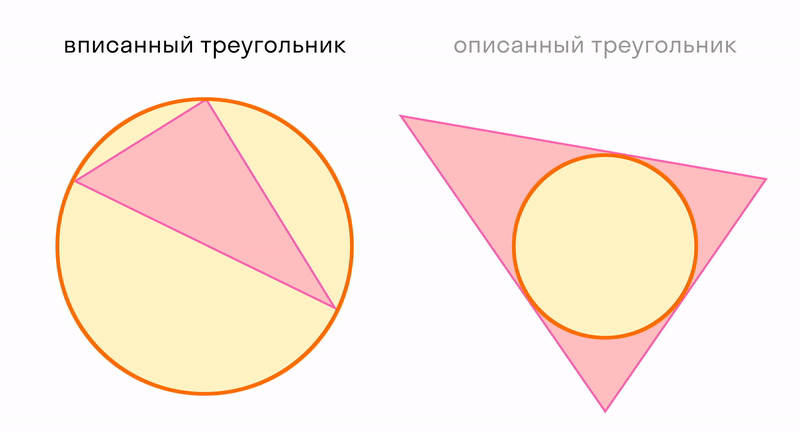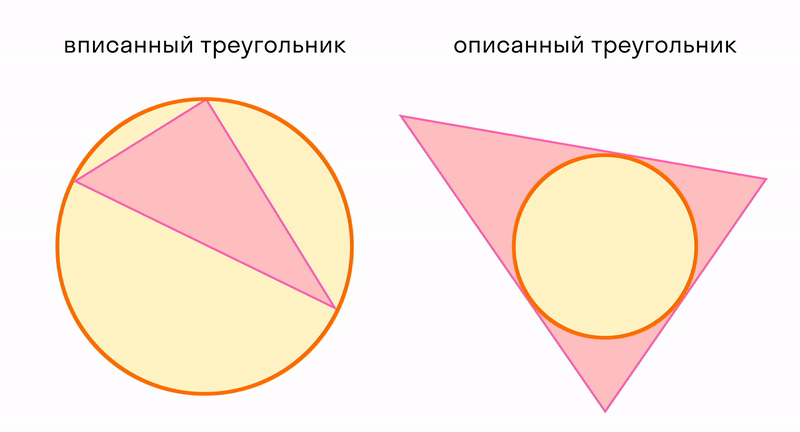Что такое смежные стороны четырехугольника

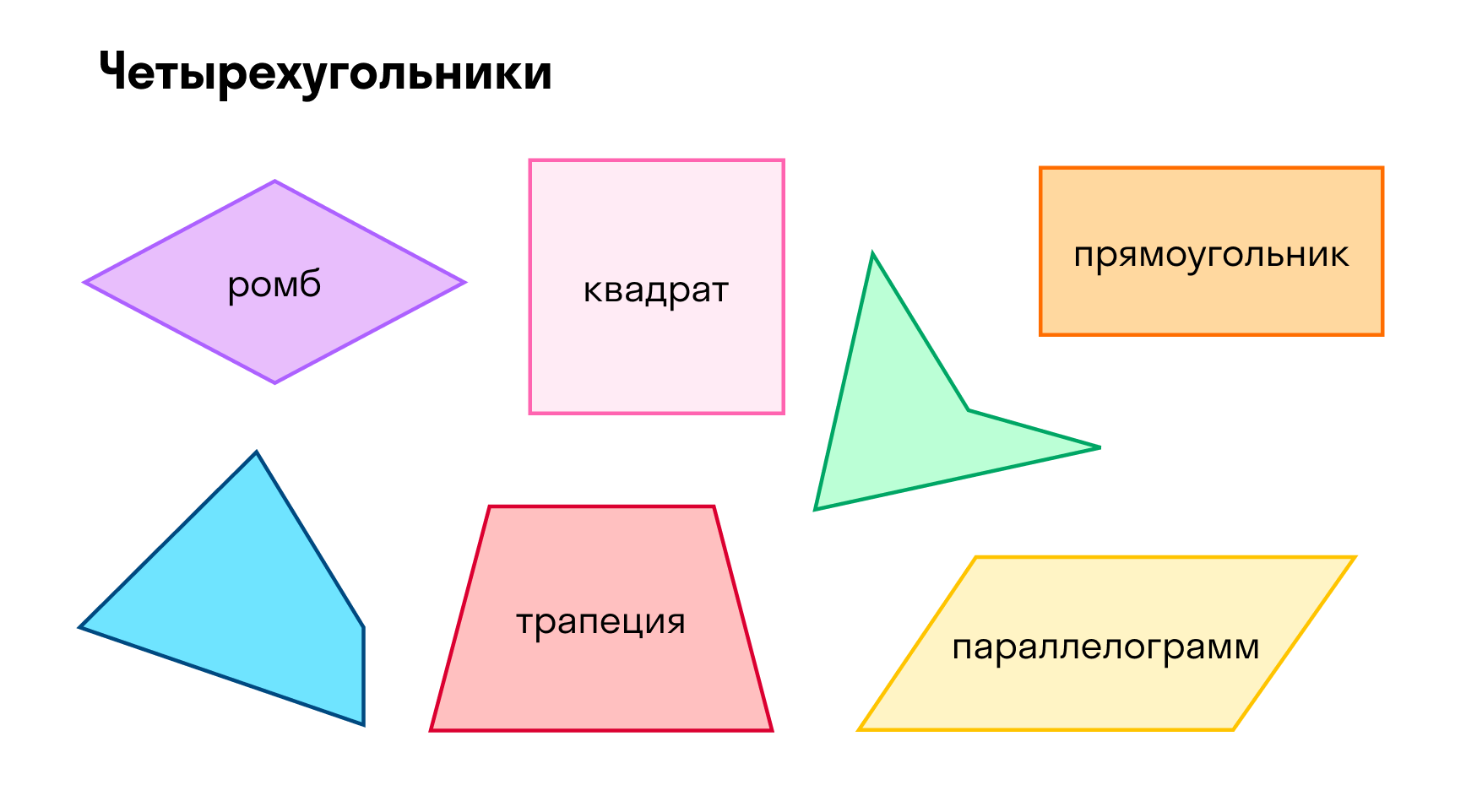
Четырехугольник

Определение четырехугольника

Определение 1. Четырехугольник − это замкнутая ломаная линия, состоящая из четырех звеньев.

Определение 2. Четырехугольник − геометрическая фигура (многоугольник), состоящая из четырех точек, никакие три из которых не лежат на одной прямой и последовательно соединенные четырьмя отрезками, называемыми сторонами четырехугольника.

Объединение четырехугольника и ограниченной им части плоскости также называют четырехугольником.

Любой четырехугольник разделяет плоскость на две части, одна из которых называется внутренней областью четырехугольника, а другая внешней областью четырехугольника.

Виды четырехугольников

Четырехугольники бывают следующих видов:

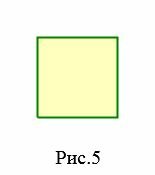Обозначение четырехугольника

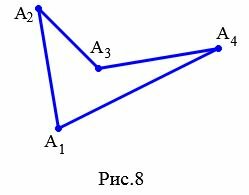
Обозначают четырехугольник буквами, стоящих при его вершинах. Называют четырехугольник чередовав буквы при его вершинах по часовой стрелке или против часовой стрелки. Например, четырехугольник на рисунке 8 называют \( \small A_1A_2A_3A_4 \) или \( \small A_4A_3A_2A_1 \) (Рис.8).

Соседние вершины четырехугольника

Вершины четырехугольника называются соседними, если они являются концами одной из его сторон.

На рисунке 8 вершины \( \small A_2 \) и \( \small A_3 \) являются соседними, так как они являются концами стороны \( \small A_2A_3. \)

Смежные стороны четырехугольника

Стороны четырехугольника называются смежными, если они имеют общую вершину.

На рисунке 8 стороны \( \small A_2A_3 \) и \( \small A_3A_4 \) являются смежными, так как они имеют общую вершину \( \small A_3. \)

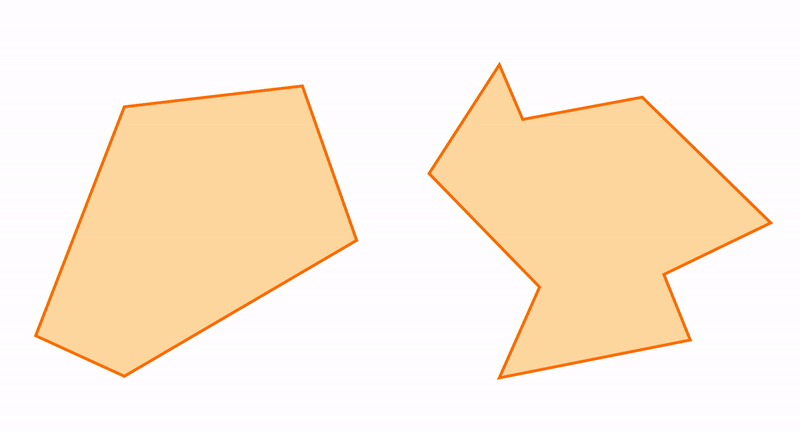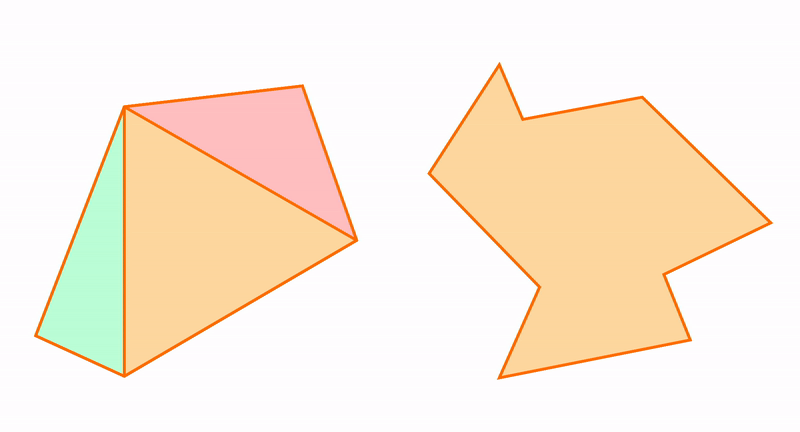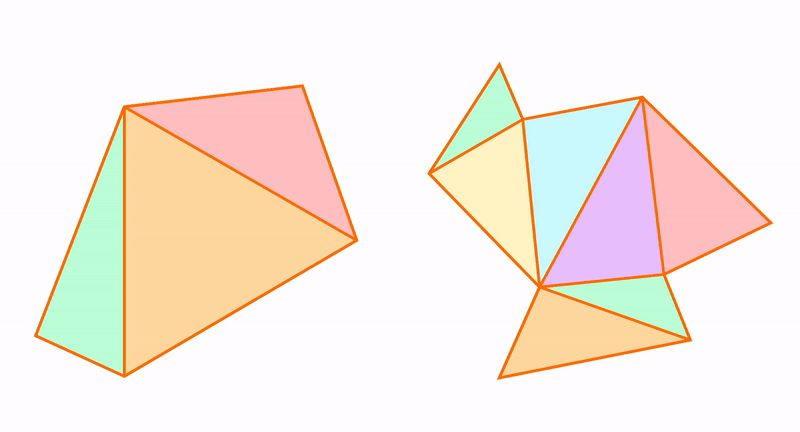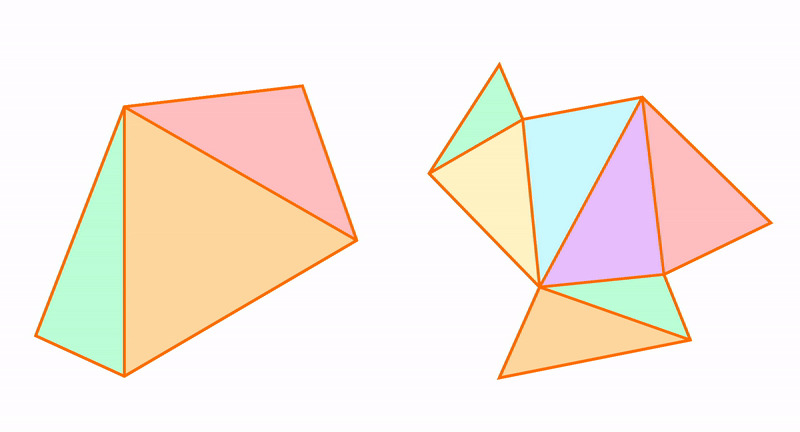
Простой четырехугольник. Самопересекающийся четырехугольник

Четырехугольник называется простым, если его несмежные стороны не имеют общих точек (внутренних или концевых).

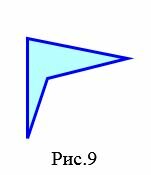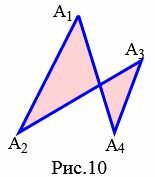На рисунках 9 и 9.1 изображены простые четырехугольники так как стороны четырехугольников не имеют самопересечений. А на рисунке 10 четырехугольник не является простым, так как стороны \( \small A_1A_4 \) и \( \small A_2A_3 \) пересекаются. Такой четырехугольник называется самопересекающийся.

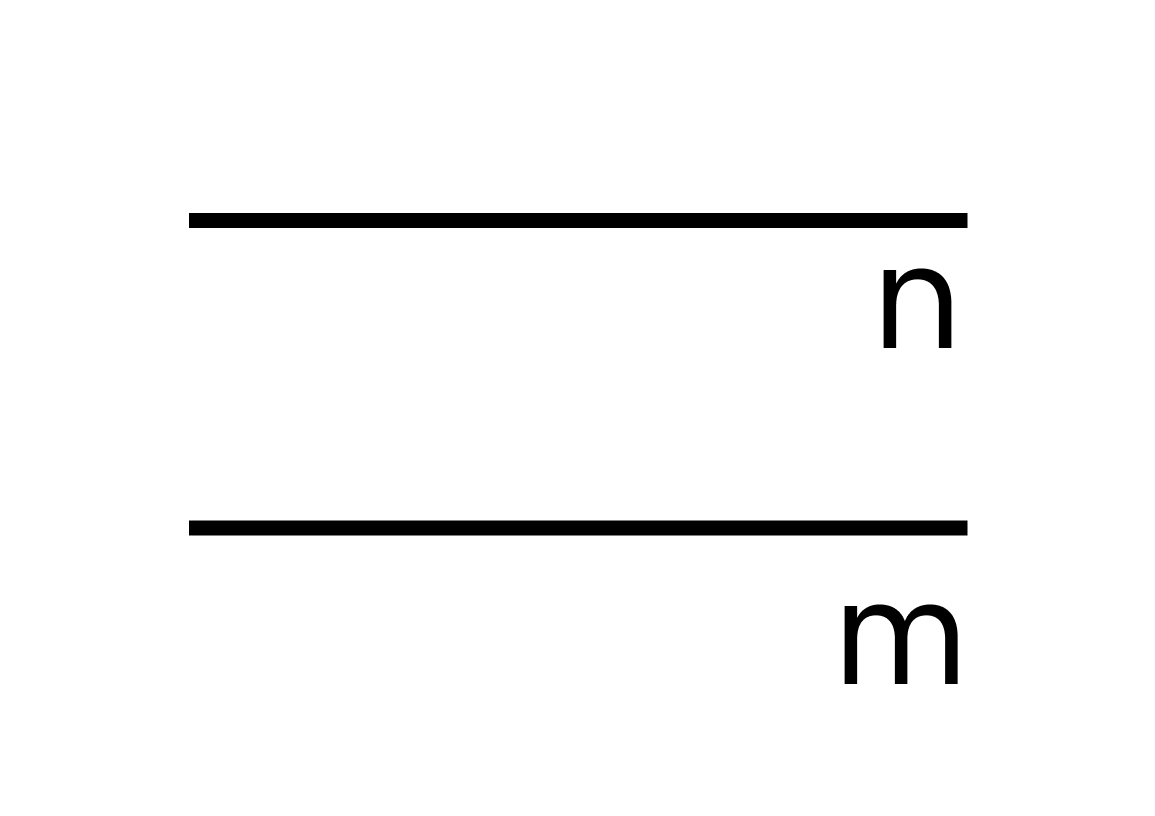
Выпуклый четырехугольник

Четырехугольник называется выпуклым, если она лежит по одну сторону от прямой, проходящей через любую его сторону.

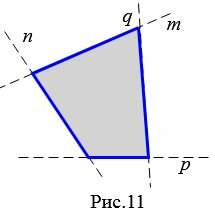На рисунке 11 четырехугольник лежит по одну сторону от прямых \( \small m, \ n, \ p, \ q, \) проходящих через стороны четырехугольника. Поэтому такой четырехугольник выпуклый.

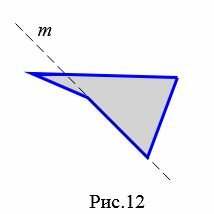На рисунке 12 прямая \( \small m\) делит четырехугольник на две части, т.е. четырехугольник не лежит по одну сторону от прямой \( \small m\). Следовательно, этот четырехугольник не является выпуклым.

Правильный четырехугольник

Простой четырехугольник называется правильным, если все его стороны равны и все углы равны. Квадрат является правильным четырехугольником, так как все его стороны равны и все его углы равны 90°. Среди четырехугольников других правильных четырехугольников не существует.

На рисунке 5 изображен правильный четырехугольник (квадрат), так как у данного четырехугольника все стороны равны и все углы равны. Четырехугольник (ромб) на на рисунке 4 не является правильным, так как все стороны четырехугольника равны, но все его углы не равны друг другу. Прямоугольник также не является правильным четырехугольником, так как несмотря на то, что все углы прямоугольника равны, но все четыре стороны прямоугольника не равны друг другу.

Периметр четырехугольника

Сумма всех сторон четырехугольника называется периметром четырехугольника. Для четырехугольника \( \small A_1A_2A_3A_4 \) периметр вычисляется из формулы:

Угол четырехугольника

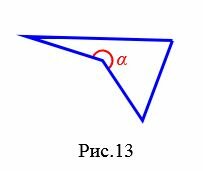
Углом (внутренним углом) четырехугольника при данной вершине называется угол между двумя сторонами четырехугольника, сходящимися к этой вершине. Если четырехугольник выпуклый, то все углы четырехугольника меньше 180°. Если же четырехугольник невыпуклый, то он имеет внутренний угол больше 180° (угол \( \small \alpha \) на рисунке 13).

Внешний угол четырехугольника

Внешним углом четырехугольника при данной вершине называется угол смежный внутреннему углу четырехугольника при данной вершине.

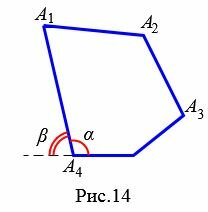На рисунке 14 угол α является внутренним углом четырехугольника при вершине \( \small A_4, \) а углы β и γ являются внешними углами четырехугольника при этой же вершине. Очевидно, что при каждой вершине есть два внешних угла.

Диагональ четырехугольника

Диагоналями называют отрезки, соединяющие две несоседние вершины четырехугольника.

Очевидно, что у четырехугольника две диагонали.

Сумма углов четырехугольника

Для любого простого четырехугольника по крайней мере один диагональ делит его на два треугольника. Сумма углов треугольника равна 180°. Поэтому сумма углов простого четырехугольника равна 360°.

Сумма внешних углов четырехугольника

Задача 1. Доказать, что длина любой стороны четырехугольника меньше суммы длин трех его сторон.

Источник

Геометрия. Урок 4. Четырехугольники

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Определение четырехугольника

Четырехугольником называется фигура, которая состоит из четырех точек (вершин) и четырех отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.

Выпуклые четырехугольники

В задачах ОГЭ встречаются выпуклые четырехугольники, поэтому подробно изучим их.

Диагонали выпуклого четырехугольника пересекаются в одной точке.

Площадь произвольного выпуклого четырехугольника можно найти по формуле:

S = 1 2 d 1 d 2 ⋅ sin φ

где d 1 и d 2 – диагонали четырехугольника, φ – угол между диагоналями (острый или тупой – не важно).

Рассмотрим более подробно некоторые виды выпуклых четырехугольников.

Класс параллелограммов : параллелограмм, ромб, прямоугольник, квадрат.

Класс трапеций : произвольная трапеция, прямоугольная трапеция, равнобокая (равнобедренная) трапеция.

Параллелограмм

Параллелограмм – четырехугольник, у которого противолежащие стороны попарно параллельны.

Свойства параллелограмма:

Площадь параллелограмма можно найти по трём формулам.

Как произведение стороны и высоты, проведенной к ней.

Поскольку стороны имеют разные длины, то высоты, которые к ним проведены, тоже будут иметь разные длины.

Как произведение двух смежных (соседних) сторон на синус угла между ними.

Как полупроизведение диагоналей на синус угла между ними.

Ромб – параллелограмм, у которого все стороны равны.

Свойства ромба:

Площадь ромба можно найти по трём формулам.

Как произведение стороны ромба на высоту ромба.

Как квадрат стороны ромба на синус угла между двумя сторонами.

Как полупроизведение диагоналей ромба.

Прямоугольник

Свойства прямоугольника:

Площадь прямоугольника можно найти по двум формулам:

Как произведение двух смежных (соседних) сторон прямоугольника.

Как полупроизведение диагоналей (так как они обе равны, обозначим их буквой d ) на синус угла между ними.

Квадрат

Квадрат – прямоугольник, у которого все стороны равны.

Свойства квадрата:

Площадь квадрата можно вычислить по двум формулам:

Как квадрат стороны.

Как полупроизведение квадратов диагоналей (диагонали в квадрате равны).

Трапеция

Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие нет.

Свойства трапеции:

Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.

Средняя линия параллельна основаниям. Её длина находится по формуле: m = a + b 2

Площадь трапеции можно найти по двум формулам:

Как полусумму оснований на высоту. Поскольку полусумма оснований есть средняя линия трапеции, можно найти площадь трапеции как произведение средней линии на высоту.

Как полупроизведение диагоналей на синус угла между ними.

Виды трапеций

Прямоугольная трапеция – трапеция, у которой два угла прямые.

Равнобокая (равнобедренная) трапеция – трапеция, у которой боковые стороны равны.

Свойство равнобокой трапеции: углы при основании равны

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с четырехугольниками

Источник

Четырёхугольники

Четырёхугольник — это выпуклый многоугольник с четырьмя углами и четырьмя сторонами. Четырёхугольник образуется замкнутой ломаной линией, состоящей из четырёх звеньев, и той частью плоскости, которая находится внутри ломаной.

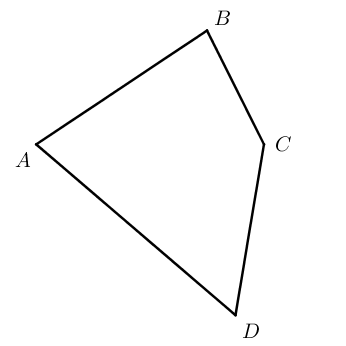
Обозначение четырёхугольника составляют из букв, стоящих при его вершинах, называя их по порядку. Например, говорят или пишут: четырёхугольник ABCD :

В четырёхугольнике ABCD точки A, B, C и D — это вершины четырёхугольника, отрезки AB, BC, CD и DA — стороны.

Вершины, принадлежащие одной стороне, называются соседними, вершины, не являющиеся соседними, называются противолежащими:

В четырёхугольнике ABCD вершины A и B, B и C, C и D, D и A — соседние, а вершины A и C, B и D — противолежащие. Углы, лежащие при соседних вершинах, также называются соседними, а при противолежащих вершинах — противолежащими.

Стороны четырёхугольника также можно попарно разделить на соседние и противолежащие: стороны, имеющие общую вершину, называются соседними (или смежными), стороны, не имеющие общих вершин — противолежащими:

Если противолежащие вершины соединить отрезком, то такой отрезок будет называться диагональю четырёхугольника. Учитывая, что в четырёхугольнике есть всего две пары противолежащих вершин, то и диагоналей может быть всего две:

Виды четырёхугольников

Рассмотрим основные виды выпуклых четырёхугольников:

Свойства углов выпуклых четырёхугольников

У всех выпуклых четырёхугольников углы обладают следующими двумя свойствами:

Источник

Что такое смежные стороны четырехугольника

Четырехугольник — фигура, состоящая из четырех точек и четырех отрезков,последовательно их соединяющих; причем ни одна из трех данных точек не лежит на одной прямой, а отрезки, соединяющие их, не пересекаются.

Соседние вершины — вершины четырехугольника, являющиеся концами одной из его сторон.
Противолежащие вершины — несоседние вершины.
Соседние стороны — стороны выходящие из одной вершины. Противолежащие стороны — несоседние стороны.
Диагональ четырехугольника — отрезок, соединяющий противолежащие вершины четырехугольника.
Периметр четырехугольника — сумма длин всех сторон.
Выпуклый четырехугoльник — четырехугольник, лежащий в одной полуплоскости относительно прямой,содержащей его сторону.
Внешний угол четырехугольника — угол,смежный с углом четырехугольника.

Свойства углов и сторон четырехугольника

Свойства углов
1. Сумма углов четырехугольника равна 360°.
2. Сумма внешних углов четырехугольника, взятых по одному при каждой вершине, равна 360°.

Свойства сторон
1. Каждая сторона четырехугольника меньше суммы всех его других сторон.
2. Сумма диагоналей меньше его периметра.

Виды четырехугольников

Конспекты по четырехугольникам:

Это конспект по теме «Четырехугольники и его свойства». Выберите дальнейшие действия:

Источник

Что такое смежные стороны

Есть 1 ответ(ов) на вопрос что такое смежные стороны

Ответы и объяснения

Смежные стороны – это соседи. Это стороны, которые имеют общую точку, например вообрази четырехугольник АБСД. Так вот, АБ и БС – это смежные стороны, т.к. они имеют общую точку Б, (соседи), а вот стороны АБ и СД – не смежные

Ваш комментарий к ответу:

Ваш комментарий к ответу:

Здравствуйте! На сайте Otvet-Master.ru собраны ответы и решения на все виды школьных задач и университетских заданий. Воспользуйтесь поиском решений на сайте или задайте свой вопрос онлайн и абсолютно бесплатно.

Ответы на вопрос Смежные стороны

Источник: http://wordparts.ru/vopros/Смежные стороны/

Идеальные объекты

Геометрия — раздел математики, который изучает пространственные структуры и отношения, а также их обобщения.

Основные геометрические объекты: окружность, квадрат, ромб, прямоугольник, равносторонний треугольник, равнобедренный треугольник, правильный многоугольник, эллипс и другие.

Все эти фигуры обладают двумя свойствами:

Равенство частей можно заметить у квадрата, ромба или равностороннего треугольника — равенство сторон. Также у них есть одна или несколько линий симметрии.

У шара бесконечное количество осей симметрии и плоскостей симметрии, но отсутствует равенство или подобие составных частей.

Все типы правильных многогранников обладают симметрией, при этом составлены из некоторого количества одинаковых фигур (треугольников, квадратов, пятиугольников).

Из всего этого можно сделать вывод, что отличить правильную геометрическую фигуру от произвольной совсем не сложно. Достаточно выяснить, имеет ли данная фигура оси или плоскости симметрии, а также из каких повторяющихся частей она состоит.

Таким образом, именно по наличию или отсутствию симметрии и равенства или подобия составных частей можно оценивать различные объекты окружающего мира на соответствие правильному геометрическому виду.

Например, возьмем два треугольника. На первый взгляд, они похожи, но у одного из них одна сторона вогнутая, вторая — выпуклая. А у другого наоборот.

Математика занимается идеальными объектами и делает о них некие заключения, которые называют теоремами. Эти треугольники похожи, и о них можно сделать близкое заключение, которое будет описывать свойства обоих.

Например, теорема Пифагора звучит так: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. А затем это свойство можно применять при решении задач и составлении чертежей.

Базовые геометрические объекты

Базовые геометрические фигуры — это точки, отрезки, лучи, прямые, плоскости.

Точка — это идеальный математический объект, у которого нет длины и ширины.

Отрезок — это часть прямой, у которого есть начало и конец.

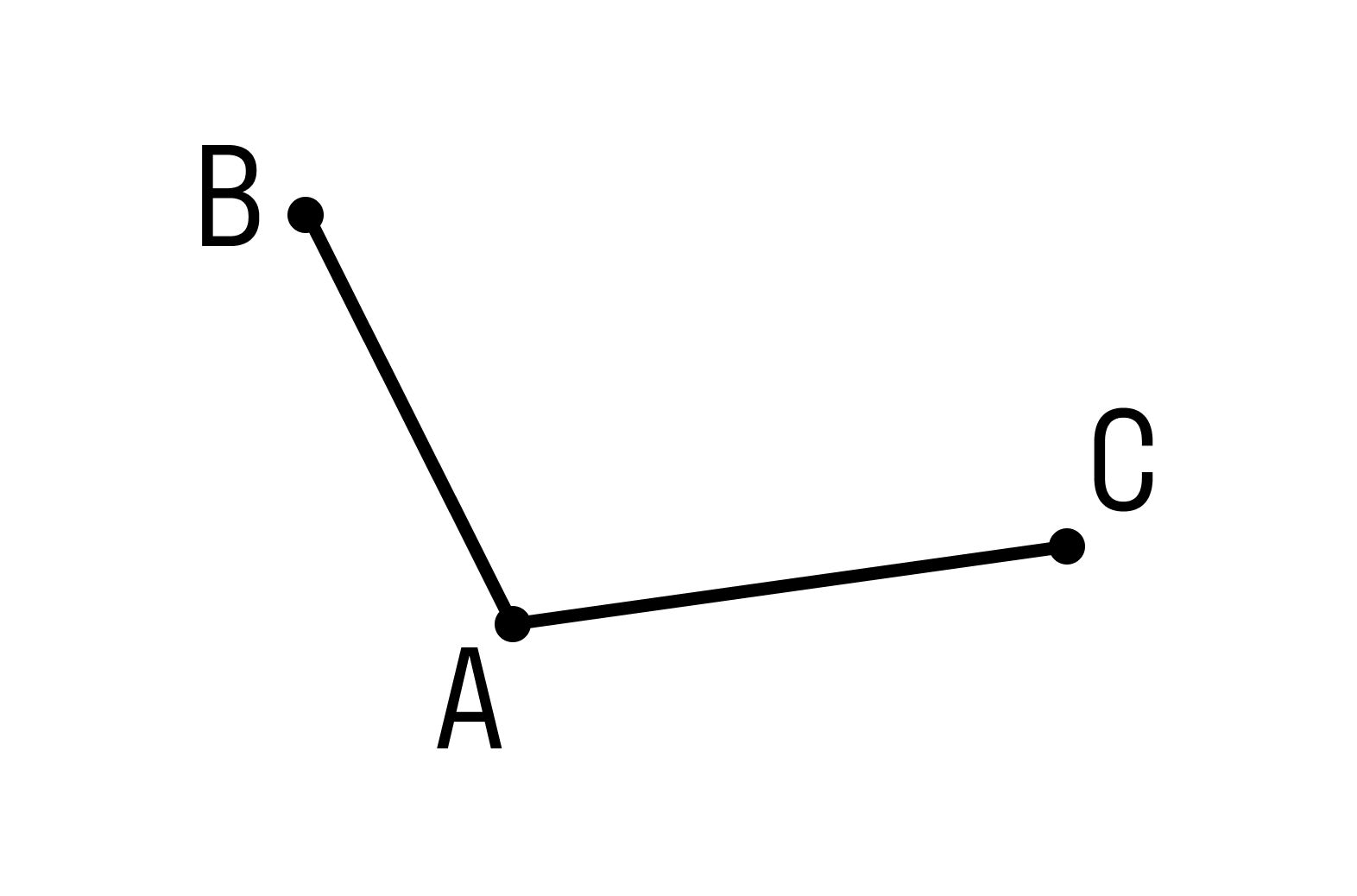
Смежные отрезки — это отрезки, которые не лежат на одной прямой и имеют один общий конец. На рисунке изобразили смежные отрезки АВ и АС, где точка А — общий конец.

Прямая — это «не кривая». Более точное определение вряд ли можно сформулировать.

Когда мы рисуем прямую на листе бумаги, мы изображаем только ее часть, потому что прямая не имеет начала и конца.

Обозначать прямые принято малыми латинскими буквами (a, b,c), но можно и большими латинскими буквами (АВ, CD, MN). Точки всегда обозначают большими латинскими буквами (А, В, С).

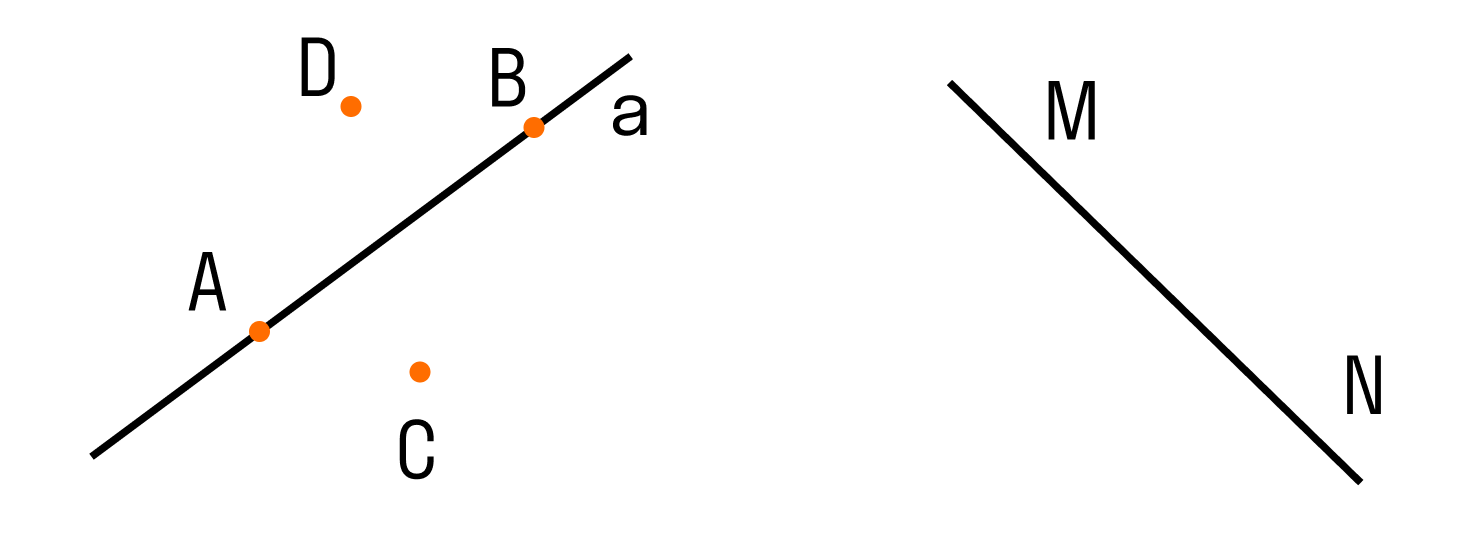
Два варианта расположения точек относительно прямой:

Через любые две точки можно провести прямую и притом только одну.

Если рассмотреть две прямые, то возможны два варианта их расположения:

Для записи не пересекающихся прямых используют специальный знак — ,
то есть m n (читают: прямая m не пересекает прямую n).

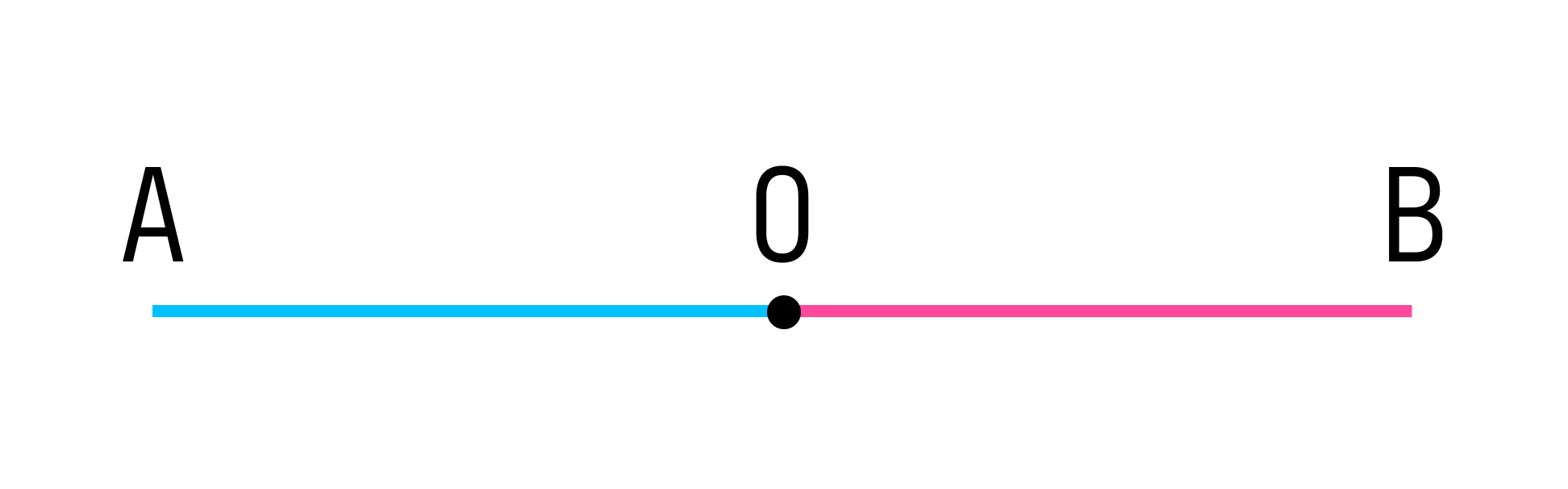
Луч — это часть прямой, ограниченная с одной стороны. Луч имеет начало, но не имеет конца.

На рисунке точка О разбивает прямую АВ на две части:

Каждая из этих частей называется лучом, а точка О является началом одного и другого луча.

Назовем получившиеся лучи:

Лучи ОА и ОВ принадлежат одной прямой АВ. Лучи ОА и ОВ имеют общее начало (точка О). Лучи ОА и ОВ противоположно направлены. При таких условиях лучи ОА и ОВ называются дополнительными.

Плоскость — это бесконечная поверхность, к которой принадлежат все прямые, которые проходят через какие-либо две точки плоскости

Треугольник

Треугольник образуют три прямые. Но на треугольник также можно посмотреть, как на фигуру, которая состоит из трех отрезков.

Из треугольников можно получить остальные многоугольники и к треугольникам можно приближать другие фигуры. Например, пятиугольник состоит из трех треугольников.

Треугольник можно использовать для измерения расстояний. А еще треугольник можно рассматривать в отношениях с окружностью, которая тоже является элементарной конструкцией. Читайте про вписанные и описанные углы.

Треугольник можно легко вычислить, то есть найти его площадь по трем элементам:

Четырехугольники

Про четырехугольники мы много говорим на уроках в школе: прямоугольник, квадрат, ромб.

Но говорим о них не в общем случае, как для треугольников (такие вещи, как теорема синусов, косинусов), а можем формулировать только какие-то свойства для определенных видов четырехугольников.

Четырехугольникам лучше уделить побольше времени — у каждого из них есть особые свойства, которые не пригодятся для других фигур. Поэтому каждый четырехугольник лучше внимательно изучить на уроке или почитать в наших материалах:

Окружность

Окружность — это еще один объект, который полезно изучить. Ее легко описать, она задается одним параметром — радиусом. А еще часто встречается в физике и в обычной жизни. Например, когда капля падает в воду, от нее остаются следы — маленткие окружности.

Практическая сторона геометрии

Название «геометрия» переводится с греческого, как «гео» — земля и «метрео» — мерить. Изначально геометрию использовали для разметки земли и других работ с землей. Но, оказалось, что сфера ее влияния безгранична.

Чтобы понять, зачем нам нужны знания по геометрии, просто оглянитесь вокруг: геометрия окружает нас в предметах разных форм. Взять хотя бы круг: его используют в искусстве, строительстве, технике. То же самое и с другими фигурами: чтобы сконструировать автомобиль или айфон, сшить одежду или построить дом — не обойтись без геометрии.

А еще геометрия помогает научиться рассуждать логически, искать связи и противоречия — полезный навык в диджитал-мире, когда информация окружает нас повсюду.

Вот, в каких профессиях пригодится геометрия: архитектор, айтишник, дизайнер, инженер, конструктор, строитель, smm-менеджер, декоратор, летчик, водитель, художник, проектировщик, астроном, спортсмен, музыкант и другие.

Почему изучать геометрию просто: мы видим объемный мир каждый день и регулярно прикасаемся к предметам, строим планы, размышляем и считаем в уме. В геометрии все знания подкреплены научными теориями — это помогает взаимодействовать с пространством по-другому, более осознанно.

Почему изучать геометрию сложно: некоторые правила придется учить наизусть.

Чтобы понять геометрию, двигайтесь от простого к сложному. Многие теоремы могут показаться очевидными. Но эта видимость может быть верной только для одного рисунка. Невозможно нарисовать все ситуации, ведь их их бесконечное множество. Именно поэтому важно доказать истину, чтобы никогда не сомневаться в ней.

Источник