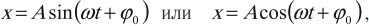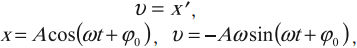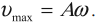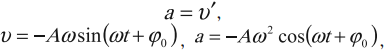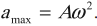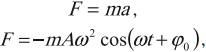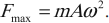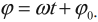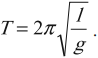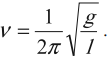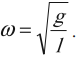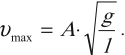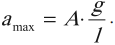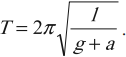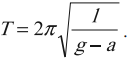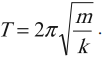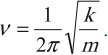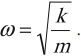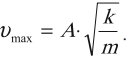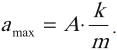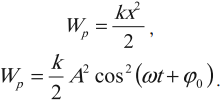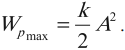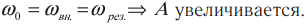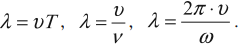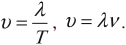Что такое собственная циклическая частота колебательной системы
Гармонические колебания
Скорость и ускорение при гармонических колебаниях
Как вы знаете, ускорение колебательного движения прямо пропорционально смещению с обратным знаком, поэтому а
Выясним, чему равны амплитудные значения скорости и ускорения.
За время, равное периоду колебаний Т, точка, двигаясь по окружности, делает один оборот, а её проекция совершает одно полное колебание. За это время точка проходит путь S, равный длине окружности, т. е. S = 2πR или S = 2πхm. Соответственно линейная скорость движения точки по окружности υ равна максимальной скорости колебаний проекции этой точки на ось ОХ:
За это же время, равное периоду, радиус-вектор точки поворачивается на угол, равный 2л, и угловая скорость точки и соответственно циклическая частота колебаний равна 
Подставив это равенство в формулу скорости, получим υm = ωхm.
Центростремительное ускорение, с которым точка движется по окружности, и соответственно амплитуда ускорения колебаний его проекции равна аm = ω 2 хm. Это равенство справедливо и для мгновенных значений смещения и ускорения: а = ω 2 x.
Учитывая полученные выражения для амплитудных значений скорости и ускорения колебаний, перепишем уравнения зависимости скорости и ускорения колебаний от времени:
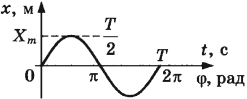
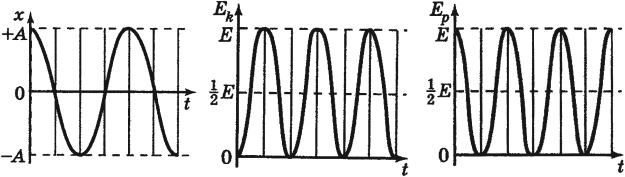
На рисунке 73 приведены графики зависимости скорости и ускорения от времени при гармонических колебаниях.
Уточним физический смысл понятия фазы колебаний. Из полученных уравнений видно, что при заданной амплитуде гармонических колебаний, зная фазу колебаний, можно в любой момент времени определить значения смещения, скорости и ускорения колебаний. Таким образом,
фаза позволяет определить состояние колебательной системы в любой момент времени.
Собственная частота колебательной системы
3. Выведенная из состояния равновесия колебательная система совершает свободные колебания с определённой частотой. Эта частота определяется параметрами системы, поэтому её называют собственной частотой колебательной системы.
Приравнивая выражения для ускорения 
и а = ω 2 x, можно сделать вывод, что для пружинного маятника собственная частота колебаний определяется равенством
Следовательно, собственная частота пружинного маятника зависит от параметров колебательной системы — массы груза и жёсткости пружины.
Аналогично можно записать формулу, выражающую зависимость частоты колебаний математического маятника от параметров этой колебательной системы. Напомним, что в данном случае колебательной системой является система «маятник — Земля». Поскольку 
и а = ω 2 x, можно записать
I. Механика
Тестирование онлайн
Колебательное движение
Колебательная система
Это система взаимодействующих тел (минимум два тела), которые способны совершать колебания. Простейшими колебательными системами являются маятники.
Характеристика колебаний
Фаза определяет состояние системы, а именно координату, скорость, ускорение, энергию и др.
Циклическая частота характеризует скорость изменения фазы колебаний.
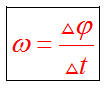
Начальное состояние колебательной системы характеризует начальная фаза 
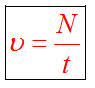
Частота, циклическая частота и период колебаний соотносятся как
Виды колебаний
Колебания, которые происходят в замкнутых системах называются свободными или собственными колебаниями. Колебания, которые происходят под действием внешних сил, называют вынужденными. Встречаются также автоколебания (вынуждаются автоматически).
Если рассматривать колебания согласно изменяющихся характеристик (амплитуда, частота, период и др.), то их можно разделить на гармонические, затухающие, нарастающие (а также пилообразные, прямоугольные, сложные).
При свободных колебаниях в реальных системах всегда происходят потери энергии. Механическая энергия расходуется, например, на совершение работы по преодолению сил сопротивления воздуха. Под влиянием силы трения происходит уменьшение амплитуды колебаний, и через некоторое время колебания прекращаются. Очевидно, что чем больше силы сопротивления движению, тем быстрее прекращаются колебания.
Вынужденные колебания. Резонанс
Вынужденные колебания являются незатухающими. Поэтому необходимо восполнять потери энергии за каждый период колебаний. Для этого необходимо воздействовать на колеблющееся тело периодически изменяющейся силой. Вынужденные колебания совершаются с частотой, равной частоте изменения внешней силы.
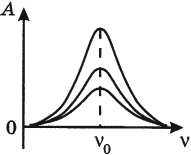
Амплитуда вынужденных механических колебаний достигает наибольшего значения в том случае, если частота вынуждающей силы совпадает с частотой колебательной системы. Это явление называется резонансом.
Например, если периодически дергать шнур в такт его собственным колебаниям, то мы заметим увеличение амплитуды его колебаний.
Примеры резонанса
Если влажный палец двигать по краю бокала, то бокал будет издавать звенящие звуки. Хотя это и незаметно, палец движется прерывисто и передает стеклу энергию короткими порциями, заставляя бокал вибрировать
Стенки бокала также начинают вибрировать, если на него направить звуковую волну с частотой, равной его собственной. Если амплитуда станет очень большой, то бокал может даже разбиться. По причине резонанса при пении Ф.И.Шаляпина дрожали (резонировали) хрустальные подвески люстр. Возникновение резонанса можно проследить и в ванной комнате. Если вы будете негромко пропевать звуки разной частоты, то на одной из частот возникнет резонанс.
Явление резонанса используется, когда с помощью небольшой силы необходимо получить большое увеличение амплитуды колебаний. Например, тяжелый язык большого колокола можно раскачать, действуя сравнительно небольшой силой с частотой, равной собственной частоте колебаний колокола.
Механические колебания.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ : гармонические колебания; амплитуда, период, частота, фаза колебаний; свободные колебания, вынужденные колебания, резонанс.
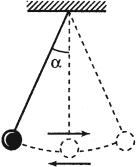
Сразу после того, как отклонённый маятник отпустили, он начал двигаться, прошёл положение равновесия, достиг противоположного крайнего положения, на мгновение остановился в нём, двинулся в обратном направлении, снова прошёл положение равновесия и вернулся назад. Совершилось одно полное колебание. Дальше этот процесс будет периодически повторяться.
Гармонические колебания.
Выясним смысл входящих в эту формулу величин.
Измеряется циклическая частота в рад/с (радиан в секунду).
В соответствии с выражениями (2) и (3) получаем ещё две формы записи гармонического закона (1) :
 |
| Рис. 1. График гармонических колебаний |
Гармонический закон вида (1) носит самый общий характер. Он отвечает, например, ситуации, когда с маятником совершили одновременно два начальных действия: отклонили на величину и придали ему некоторую начальную скорость. Имеются два важных частных случая, когда одно из этих действий не совершалось.
 |
| Рис. 2. Закон косинуса |
 |
| Рис. 3. Закон синуса |
Уравнение гармонических колебаний.
Теперь дифференцируем полученное равенство (4) :
Давайте сопоставим выражение (1) для координаты и выражение (5) для проекции ускорения. Мы видим, что проекция ускорения отличается от координаты лишь множителем :
Это соотношение называется уравнением гармонических колебаний. Его можно переписать и в таком виде:
C математической точки зрения уравнение (7) является дифференциальным уравнением. Решениями дифференциальных уравнений служат функции (а не числа, как в обычной алгебре).
Так вот, можно доказать, что:
-решением уравнения (7) является всякая функция вида (1) с произвольными ;
-никакая другая функция решением данного уравнения не является.
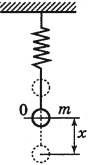
Пружинный маятник.
Найдём период малых горизонтальных колебаний пружинного маятника (рис. 4 ). Колебания будут малыми, если величина деформации пружины много меньше её размеров. При малых деформациях мы можем пользоваться законом Гука. Это приведёт к тому, что колебания окажутся гармоническими.
Координате отвечает положение равновесия, в котором пружина не деформирована. Следовательно, величина деформации пружины равна модулю координаты груза.
 |
| Рис. 4. Пружинный маятник |
В горизонтальном направлении на груз действует только сила упругости со стороны пружины. Второй закон Ньютона для груза в проекции на ось имеет вид:
Тогда соотношение (8) принимает вид:
Циклическая частота колебаний пружинного маятника, таким образом, равна:
Отсюда и из соотношения находим период горизонтальных колебаний пружинного маятника:
Математический маятник.
 |
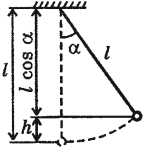
| Рис. 5. Математический маятник |
Запишем для маятника второй закон Ньютона:
и спроектируем его на ось :
Если маятник занимает положение как на рисунке (т. е. 0′ alt=’x>0′ /> ), то:
Если же маятник находится по другую сторону от положения равновесия (т. е. ), то:
Итак, при любом положении маятника имеем:
Следовательно, циклическая частота колебаний математического маятника равна:
Отсюда период колебаний математического маятника:
Обратите внимание, что в формулу (13) не входит масса груза. В отличие от пружинного маятника, период колебаний математического маятника не зависит от его массы.
Свободные и вынужденные колебания.
Говорят, что система совершает свободные колебания, если она однократно выведена из положения равновесия и в дальнейшем предоставлена сама себе. Никаких периодических внешних
воздействий система при этом не испытывает, и никаких внутренних источников энергии, поддерживающих колебания, в системе нет.
Рассмотренные выше колебания пружинного и математического маятников являются примерами свободных колебаний.
Частота, с которой совершаются свободные колебания, называется собственной частотой колебательной системы. Так, формулы (9) и (12) дают собственные (циклические) частоты колебаний пружинного и математического маятников.
В идеализированной ситуации при отсутствии трения свободные колебания являются незатухающими, т. е. имеют постоянную амплитуду и длятся неограниченно долго. В реальных колебательных системах всегда присутствует трение, поэтому свободные колебания постепенно затухают (рис. 6 ).
 |
| Рис. 6. Затухающие колебания |
В течение некоторого времени происходит установление вынужденных колебаний: система совершает сложное движение, которое является наложением выужденных и свободных колебаний. Свободные колебания постепенно затухают, и в установившемся режиме система совершает вынужденные колебания, которые также оказываются гармоническими. Частота установившихся вынужденных колебаний совпадает с частотой
вынуждающей силы (внешняя сила как бы навязывает системе свою частоту).
 |
| Рис. 7. Резонанс |
Что такое собственная циклическая частота колебательной системы
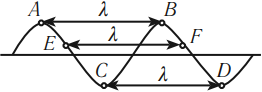
Отличие колебания от волны
Период колебаний T – интервал времени, в течение которого происходит одно полное колебание.
Частота колебаний ν – число полных колебаний в единицу времени. В системе СИ выражается в герцах (Гц).
Период и частота колебаний связаны соотношением:
 |
Циклическая (или круговая) частота ω = 2πν. Она связана с периодом отношением:
 |
Гармонические колебания – это колебания, при которых колеблющаяся величина изменяется по закону синуса или косинуса. Смещение определяется формулой:
 |
где x 0 – амплитуда, ω – циклическая частота, φ0 – начальная фаза колебания. Дифференциальное уравнение свободных гармонических механических колебаний имеет один и тот же вид для любых колебаний:
 |
где 
– ускорение тела. Величина ω0 называется собственной частотой свободных колебаний. Ускорение при гармонических колебаниях всегда направлено в сторону, противоположную смещению; максимальное ускорение равно 
|
