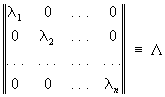
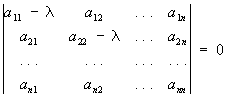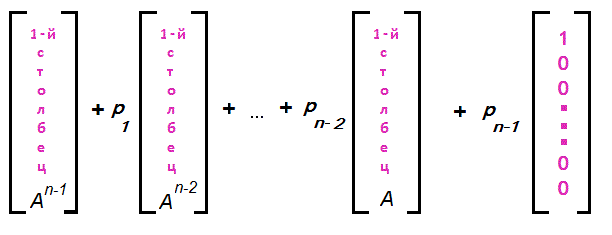Что такое собственные числа

Собственные значения

Полезное

Смотреть что такое «Собственные значения» в других словарях:

собственные значения — линейного преобразования, скаляры, на которые умножаются его собственные векторы. Таким образом, λ есть собственные значения преобразования А, если существует ненулевой вектор х такой, что Ах = λх. * * * СОБСТВЕННЫЕ ЗНАЧЕНИЯ СОБСТВЕННЫЕ ЗНАЧЕНИЯ… … Энциклопедический словарь

СОБСТВЕННЫЕ ЗНАЧЕНИЯ — линейного преобразования, скаляры, на к рые умножаются его собств. векторы. Т.о., Я. есть С. з. преобразования А, если существует ненулевой вектор х такой, что Ах = Лямбда х … Естествознание. Энциклопедический словарь

Собственные значения — … Википедия

СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ ОПЕРАТОРОВ; — численные методы нахождения методы вычисления собственных значений и соответствующих собственных функций дифференциальных операторов. Колебания упругих ограниченных тел описываются уравнением где нек рое дифференциальное выражение. Если решение… … Математическая энциклопедия

СОБСТВЕННЫЕ ЗНАЧЕНИЯ ИНТЕГРАЛЬНЫХ ОПЕРАТОРОВ — численные методы нахождения методы вычисления полного спектра интегрального оператора или его части (чаще всего ставится задача отыскания одного двух минимальных или максимальных по модулю собственных значений). Сопутствующей задачей часто бывает … Математическая энциклопедия

Собственные векторы — Собственные векторы, значения и пространства Красным цветом обозначен собственный вектор. Он, в отличие от синего, при деформации не изменил направление и длину, поэтому является собственным вектором, соответствующим собственному значению λ = 1.… … Википедия

Собственные векторы, значения и пространства — Синим цветом обозначен собственный вектор. Он, в отличие от красного, при деформации(преобразовании) не изменил направление и длину, поэтому является собственным вектором, соответствующим … Википедия

Собственные функции — понятие математического анализа. При решении многих задач математической физики (в теории колебаний, теплопроводности и т.д.) возникает необходимость в нахождении не равных тождественно нулю решений однородных линейных дифференциальных… … Большая советская энциклопедия

Собственные векторы — линейного преобразования, векторы, которые при этом преобразовании не меняют своего направления, а только умножаются на скаляр. Например, С. в. преобразования, составленного из вращении вокруг некоторой оси и сжатия к перпендикулярной ей… … Большая советская энциклопедия

Источник

Собственное число

Смотреть что такое «Собственное число» в других словарях:

Собственное движение — Собственным движением называются изменения координат звёзд на небесной сфере, вызванные относительным движением звёзд и Солнечной системы. В них не включают периодические изменения, вызванные движением Земли вокруг Солнца (параллакс). Более… … Википедия

СОБСТВЕННОЕ ЗНАЧЕНИЕ — оператора (преобразования) А векторного пространства Lнад полем k элемент такой, что существует ненулевой вектор удовлетворяющий условию Вектор хв этом равенстве наз. собственным векторам оператора А, принадлежащим С. з. В случае, когда оператор… … Математическая энциклопедия

СОБСТВЕННОЕ УДЕРЖАНИЕ СТРАХОВАТЕЛЯ В ФОРМЕ ЕЖЕДНЕВНОЙ СТОИМОСТИ — В страховании имущества: собственное удержание страхователя, применяемое при страховании предпринимательского дохода, которое выражается в определенном количестве дней. После наступления ущерба определяется сумма, которая могла быть заработана за … Страхование и управление риском. Терминологический словарь

Характеристическое число — Характеристическое число: То же что собственное число, собственное значение матрицы; корень характеристического многочлена, принадлежащий числовому полю; Значение характеристического класса касательного расслоения замкнутого многообразия на… … Википедия

ХАРАКТЕРИСТИЧЕСКОЕ ЧИСЛО — 1) X.ч. то же, что собственное число, собственное значение матрицы (см. Характеристический многочлен). 2)X. ч. значение характеристического класса касательного расслоения замкнутого многообразия на фундаментальном цикле этого многообразия. А. Ф.… … Математическая энциклопедия

Характеристическое число матрицы — Красным цветом обозначен собственный вектор. Он, в отличие от синего, при деформации не изменил направление и длину, поэтому является собственным вектором, соответствующим собственному значению λ = 1. Любой вектор, параллельный красному вектору,… … Википедия

2 (число) — У этого термина существуют и другие значения, см. 2 (значения). 2 два 1 · 0 · 1 · 2 · 3 · 4 · 5 Факторизация: Простое Римская запись: II Двоичное: 10 Восьмеричное: 2 Шестнадц … Википедия

ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ С СИММЕТРИЧНЫМ ЯДРОМ — интегральное уравнение (и. у.) с симметричным действительным ядром: К( х, s) = K(s, x). Теория линейных и. у. с симметричным и действительным ядром была впервые построена Д. Гильбертом (D. Hilbert, 1904) привлечением теории симметричных… … Математическая энциклопедия

Дискретный оператор Лапласа — О дискретном эквиваленте преобразования Лапласа см. Z преобразование. В математике дискретный оператор Лапласа аналог непрерывного оператора Лапласа, определяемого как отношения на графе или дискретной сетке. В случае конечномерного графа… … Википедия

Источник

Что такое собственные числа

Рассмотрим линейную однородную систему \(n\) дифференциальных уравнений с постоянными коэффициентами, которую можно записать в матричном виде как \[\mathbf\left( t \right) = A\mathbf\left( t \right),\] где приняты следующие обозначения: \[ <\mathbf\left( t \right) = \left( <\begin<*<20>> <\left( t \right)>\\ <\left( t \right)>\\ \vdots \\ <\left( t \right)> \end> \right),>\;\; <\mathbf\left( t \right) = \left( <\begin<*<20>> <\left( t \right)>\\ <\left( t \right)>\\ \vdots \\ <\left( t \right)> \end> \right),>\;\; <*<20>> <>>&<>>& \cdots &<>>\\ <>>&<>>& \cdots &<>>\\ \cdots & \cdots & \cdots & \cdots \\ <>>&<>>& \cdots &<>> \end> \right).> \] Будем искать нетривиальные решения однородной системы в виде \[\mathbf\left( t \right) = >\mathbf,\] где \(\mathbf \ne 0\) − постоянный \(n\)-мерный вектор, который мы определим позже.

Таким образом, мы приходим к выводу, что для того, чтобы векторная функция \(\mathbf\left( t \right) = >\mathbf\) являлась решением линейной однородной системы, необходимо и достаточно, чтобы число \(\lambda\) было собственным значением, а вектор \(\mathbf\) − соответствующим собственным вектором линейного преобразования \(A.\)

Как видно, решение линейной системы уравнений можно построить алгебраическим методом. Поэтому приведем далее некоторые необходимые сведения из линейной алгебры.

Вернемся к полученному выше матрично-векторному уравнению \[A\mathbf = \lambda \mathbf.\] Его можно переписать как \[A\mathbf — \lambda \mathbf = \mathbf<0>,\] где \(\mathbf<0>\) означает нулевой вектор.

Детальное описание этих способов решения приводится отдельно на указанных web-страницах. Ниже мы рассмотрим примеры систем дифференциальных уравнений, соответствующие случаям \(1\) и \(2.\)

Общее решение системы уравнений записывается в виде \[\mathbf\left( t \right) = >\left( <\begin<*<20>> 1\\ 0 \end> \right) + >\left( <\begin<*<20>> 0\\ 1 \end> \right).\]

Источник

Собственный вектор

Из Википедии — свободной энциклопедии

Понятия собственного вектора и собственного числа [3] являются одними из ключевых в линейной алгебре, на их основе строится множество конструкций. Это связано с тем, что многие соотношения, связанные с линейными операторами, существенно упрощаются в системе координат, построенной на базисе из собственных векторов оператора. Множество собственных значений линейного оператора (спектр оператора) характеризует важные свойства оператора без привязки к какой-либо конкретной системе координат. По этим причинам собственные векторы имеют важное прикладное значение. Так, например, собственные векторы часто встречаются в механике, квантовой теории и так далее. В частности, оператор проекции спина на произвольную ось имеет два собственных и соответствующие им собственные векторы.

Понятие линейного векторного пространства не ограничивается «чисто геометрическими» векторами и обобщается на разнообразные множества объектов, таких как пространства функций (в которых действуют линейные дифференциальные и интегральные операторы). Для такого рода пространств и операторов говорят о собственных функциях операторов.

Множество всех собственных векторов линейного оператора, соответствующих данному собственному числу, дополненное нулевым вектором, называется собственным подпространством [4] этого оператора.

Поиск оптимальных алгоритмов вычисления собственных значений для заданного линейного оператора является одной из важных задач вычислительной математики.

Источник

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Характеристический полином, собственные числа, собственные векторы матрицы

Характеристический полином

Теорема 1.

Пример. Характеристический полином матрицы Фробениуса

Характеристический полином линейного оператора

определяется как характеристический полином матрицы этого оператора в произвольном базисе линейного пространства, в котором этот оператор задан. Подробнее ☞ ЗДЕСЬ.

Характеристический полином линейного однородного разностного уравнения

Свойства

Теорема 2. Характеристический полином матрицы не меняется

Теорема Гамильтона-Кэли

матрица является корнем своего характеристического полинома.

Доказательство ☞ ЗДЕСЬ.

Собственное число

Пример. Найти спектр матрицы

Доказательство следует из представления характеристического полинома через миноры матрицы и формул Виета. ♦

Имеет место следующее равенство:

Доказательство ☞ ЗДЕСЬ.

Доказательство ☞ ЗДЕСЬ.

Доказательство ☞ ЗДЕСЬ.

Теорема 11. Спектр циклической матрицы

Доказательство ☞ ЗДЕСЬ.

Локализация собственных чисел

Теорема 12. [1]. Собственные числа матрицы являются непрерывными функциями ее элементов. Иначе: пусть

Собственно факт непрерывной зависимости собственных чисел от элементов матрицы следует из представления характеристического полинома из теоремы ☞ ПУНКТА — коэффициенты этого полинома полиномиально (и, следовательно, непрерывно) зависят от элементов матрицы. Далее используем теорему о непрерывной зависимости корней полинома от его коэффициентов.

Выясним теперь на примере, насколько малым может быть возмущение элементов матрицы чтобы сохранились хотя бы количество вещественных корней ее характеристического полинома.

Пример [Уилкинсон] [2]. Найти собственные числа матрицы

Пример. Найти собственные векторы матрицы

Еще один способ нахождения собственного вектора основан на теореме Гамильтона-Кэли.

Пример. Найти собственные векторы матрицы

Пример. Вычислить собственный вектор матрицы

Пример. Найти представление всех собственных векторов матрицы

Доказательство ☞ ЗДЕСЬ.

Теорема Перрона-Фробениуса

Пример. Найти собственное число и вектор Перрона-Фробениуса для матрицы

Пример. Спектр неотрицательной матрицы

Методы вычисления характеристического полинома

А в качестве усугубляющего положение обстоятельства «на заднем плане» маячит проблема точности вычислений коэффициентов характеристического полинома — чувствительность его корней к возмущению его коэффициентов бывает весьма высокой.

Метод Леверье

Пример [Леверье]. Найти характеристический полином матрицы

Пример. Для приведенного выше примера находим собственные числа:

Теорема 21. Характеристический полином явно выражается через суммы Ньютона с помощью следующего представления:

Биографические заметки о Леверье ☞ ЗДЕСЬ.

Метод Крылова

Теорема 22. Определитель

Пример. Найти характеристический полином матрицы примера Леверье

Пример. Найти характеристический полином матрицы

Поиск всех собственных чисел

Существуют методы нахождения спектра матрицы, не требующие предварительного построения характеристического полинома.

QR-алгоритм

Частичная проблема собственных чисел

Теорема 25. Как правило, предел

Как правило, вектор

Пример. Для матрицы

Теперь обсудим исключительные случаи алгоритма.

Пример. Найти максимальное по модулю собственное число матрицы примера Леверье

Пример. Для матрицы

При выполнении условия предположения 2 имеет место равенство

Пример. Для матрицы

Задачи

Источники

[2]. Уилкинсон Дж.Х. Алгебраическая проблема собственных значений. М.Наука. 1970, с.93-94

[3]. Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. М.ГИФМЛ. 1960

[4]. Хорн Р., Джонсон Ч. Матричный анализ. М.Мир.1989

Источник