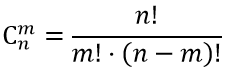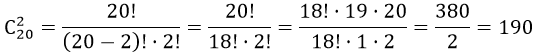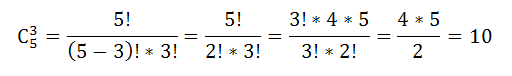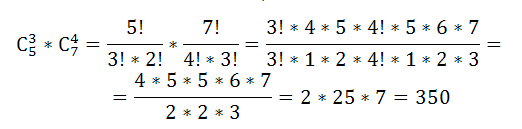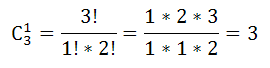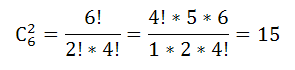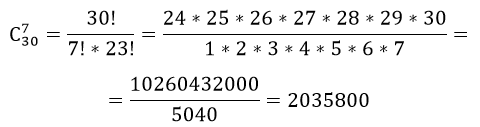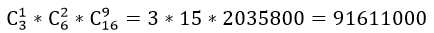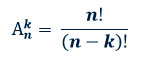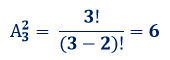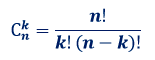Что такое сочетания без повторений

Сочетание без повторений

Сочетанием без повторений называют комбинации, составленные из n элементов по m элементам, которые отличаются друг от друга хотя бы одним элементом.

При подсчете числа сочетаний элементов — порядок не важен.

Запишем формулу сочетания

В классе 20 учащихся. Сколькими способами можно выделить двух человек для дежурства? Так как каждая группа учащихся в 2 человека должна отличаться хотя бы одним из учащихся. Отсюда, применим формулу комбинаторики — сочетание, имеем

Пусть имеется множество, содержащие 4 буквы: <А,В,С,D>.

Записать все возможные сочетания из указанных букв по три.

По формуле сочетания имеем,

В ящике 15 деталей, среди которых 6 бракованных. Наугад выбирается комплект из 5 деталей. Сколькими способами можно составить такой комплект, в котором 2 детали бракованные?

$C_<6>^2$ — количество способов выбора двух бракованных деталей из шести
$C_<9>^3$ — количество способов выбора трех исправных деталей из девяти
Тогда количество комбинаций по правилу умножения будет
$C_<6>^2·C_<9>^3=\frac<<6!>><<(6-2)!2!>>·\frac<<9!>><<(9-3)!3!>>=15·84=1260$

Сколькими способами можно распределить три путевки в один санаторий между пятью желающими?

Решение
Так как путевки предоставлены в один санаторий, то варианты распределения отличаются друг от друга хотя бы одним желающим. Поэтому число способов распределения равно

Пример 5
В научном конкурсе участвует 12 человек, из них 5 женщин и 7 мужчин. Сколькими способами можно сформировать группу из 7 человек, чтобы в ней было 3 женщины?

По формуле комбинаторики – сочетания, группу можно сформировать способами:

Сколькими способами можно составить суточный наряд по университету из одного офицера, двух сержантов и семи курсантов, если имеется 3 офицера, 6 сержантов и 30 курсантов?

Итак, получаем число способов составления суточного наряда

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 5 / 5. Количество оценок: 13

Источник

Сочетания

п.1. Сочетания без повторений

п.2. Сочетания с повторениями

п.3. Биномиальные коэффициенты и их свойства

Свойства биномиальных коэффициентов

Вынесение за скобки

Если n – четное, то максимальное значение \(\mathrm\) имеет при \(\mathrm<2>>\).
Если n – нечетное, то максимальное значение имеют два коэффициента \(\mathrm\), при \(\mathrm<2>>\) и \(\mathrm<2>>\)

Связь с числами Фибоначчи

п.4. Примеры

Пример 1. На столе лежит 10 яблок и 5 груш.
1) Сколькими способами можно выбрать 7 фруктов?
2) Сколькими способами можно выбрать 7 фруктов, чтобы среди них было 3 груши?

Пример 3. Рота состоит из 3 офицеров, 6 сержантов и 15 рядовых. Сколькими способами можно выбрать из них отряд, состоящий из 1 офицера, 2 сержантов и 5 рядовых?

По всем трём множествам делаем неупорядоченную выборку (т.е., сочетания) без повторений.
Выбираем офицеров: \(\mathrm\)
Выбираем сержантов: \(\mathrm<1\cdot 2>=15>\)
Выбираем рядовых: \(\mathrm^6=\frac<15\cdot 14\cdot 13\cdot 12\cdot 11><1\cdot 2\cdot 3\cdot 4\cdot 5>=3003>\)
По правилу произведения, отряд можно выбрать:
\(\mathrm<3\cdot 15\cdot 3003=135135>\) способами.
Ответ: 135135.

Пример 5. Рассчитайте все \(\mathrm^k>\) по рекуррентной формуле \(\mathrm^k=\fracC_n^>\).
Постройте график \(\mathrm^k(k)>\). Сделайте выводы.

Начальное значение \(\mathrm^0=1>\).

Источник

Перестановки, размещения и сочетания. Формулы.

Чтобы в материале было легче ориентироваться, добавлю содержание данной темы:

Введение. Множества и выборки.

В этой теме рассмотрим основные понятия комбинаторики: перестановки, сочетания и размещения. Выясним их суть и формулы, по которым можно найти их количество.

Для работы нам понадобятся кое-какие вспомогательные сведения. Начнём с такого фундаментального математического понятия как множество. Подробно понятие множества было раскрыто в теме «Понятие множества. Способы задания множеств».

Очень краткий рассказ про множества: показать\скрыть

Заметьте, что в определении выборки ничего не сказано про повторения элементов. В отличие от элементов множеств, элементы выборки могут повторяться.

Запись «n!» (читается «эн факториал») обозначает произведение всех чисел от 1 до n, т.е.

Нас же интересует общее количество этих размещений. Согласно формуле (1) количество размещений без повторений из 5 элементов по 3 будет таким:

Т.е. можно составить 60 трёхсимвольных слов, буквы которых не будут повторяться.

Следовательно, из заданных цифр можно составить 243 пятизначных числа.

В морозилке лежат пять порций мороженого от различных фирм. Сколькими способами можно выбрать порядок их съедения?

Следовательно, существует 120 порядков выбора очередности съедения.

Перестановки с повторениями

Общее количество перестановок с повторениями определяется формулой:

Следовательно, общее количество искомых слов равно 105.

В корзине размещены карточки, на которых написаны целые числа от 1 до 10. Из корзины вынимают 4 карточки и суммируют числа, написанные на них. Сколько различных наборов карточек можно вытащить из корзины?

Следовательно, общее количество искомых наборов равно 210.

Представьте себе, что мы находимся на конфетном заводе, – прямо возле конвейера, по которому движутся конфеты четырёх сортов. Мы запускаем руки в этот поток и вытаскиваем двадцать штук. Сколько всего различных «конфетных комбинаций» может оказаться в горсти?

Следовательно, общее количество искомых комбинаций равно 1771.

Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).

Источник

Генерация сочетаний

В комбинаторике сочетанием из N различных элементов по M называется набор M элементов, выбранных из множества N элементов. Такие наборы отличаются только вхождением в них M определенных элементов, порядок следования элементов в таком наборе не важен. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, и этим сочетания отличаются от размещений.

Сочетания без повторений

Задача : Найти все возможные сочетания без повторений из множества элементов <1,2,3>по 2.
Существуют следующие сочетания:

1: 1 2
2: 1 3
3: 2 3

Количество возможных сочетаний без повторений из N элементов по M можно определить по формуле (N≥M):

что в M! раз меньше соответствующего количества размещений без повторений (поскольку сочетания без повторений не зависят от порядка следования элементов).

Рассмотрим задачу получения всех сочетаний для чисел 1…N по M.

Результат выполнения

Сочетания с повторениями

Сочетаниями с повторениями называются наборы по M элементов, в которых каждый элемент множества N может участвовать несколько раз. При этом на соотношение значений M и N не накладывается никаких ограничений, а общее количество сочетаний с повторениями составляет

Примером такой задачи может служить выбор M открыток из N всеми возможными способами.

Для генерации сочетаний с повторениями воспользуемся решением для генерации размещений с повторениями, рассмотренным в этой статье.

Результат работы приведенного выше алгоритма:

Источник

Рассмотрим сначала некоторые общие термины.

Размещения без повторений.

Размещениями без повторений называются упорядоченные выборки, содержащие k различных элементов из данных n элементов.

Обратим внимание на следующие важные положения:

Формула для определения числа размещений без повторений:

Задача. Дана последовательность символов А, Б, С. Сколько вариантов кода, состоящего из двух разных символов, можно составить из заданной последовательности?

Действительно, комбинаций, удовлетворяющих условию, всего шесть:

Перестановки без повторений.

Нетрудно заметить, что размещения, в которые входят все n разных элементов заданного множества (т. е. k = n ), будут отличаться только порядком следования входящих элементов. Такие размещения называют перестановками.

Перестановками без повторений называются всевозможные упорядоченные выборки, составленные из всех данных n элементов.

Формула для определения числа перестановок без повторений
P_n = n! = n * (n − 1) * (n − 2) *. * 2 * 1

Задача. Сколько вариантов кода длиной 3 символа можно составить из трех букв А, Б, С, если каждая буква входит в последовательность не более одного раза?

Решение. Так как «каждая буква входит в последовательность не более одного раза», то выборки – перестановки без повторений.
P_n = 3! = 3 * 2 * 1 = 6

Сочетания без повторений.

Сочетаниями без повторений называются неупорядоченные выборки, содержащие k различных элементов из данных n элементов.

Формула для определения числа сочетаний без повторений:

Задача. Из 4-х кандидатов происходят выборы участников конференции. Сколько существует вариантов выбора делегации?

Решение. Очевидно, один и тот же кандидат в данную выборку может быть избран только один раз. При этом набор А, Б и Б, А – это одни те же участники. Поэтому выборки есть сочетания без повторений.

Воспользуемся формулой для расчета числа различных сочетаний без повторений:

Copyright © 2014-2021, Урок информатики
Все права защищены

Источник