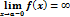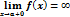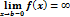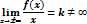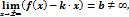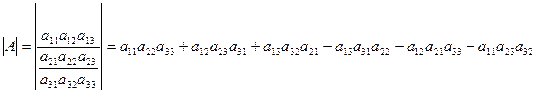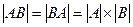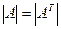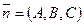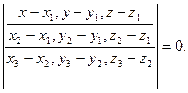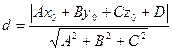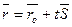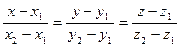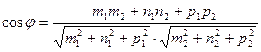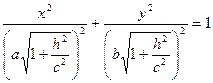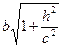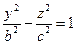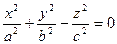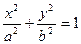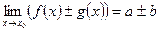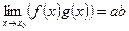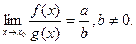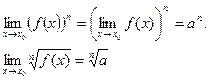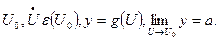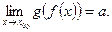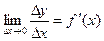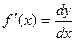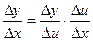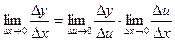Что такое согласованные матрицы
Согласованные матрицы. Умножение матриц и его свойства.
Матрицы и их виды.
Матрица размером m*n –совокупность m*n чисел расположенных в виде таблицы.Из m-строк и n-столбцов.
— Матрица, все элементы, которой равны нулю наз. нулевой.
— Матрица, у которой число строк равно числу столбцов наз. квадратной.
— Квадратная матрица, у которой все элементы, кроме элемента главной диагонали равны нулю, наз. диагональной.
Диагональная матрица у которой каждый элемент =1, наз. единичной.
2.Сложение матриц и умножение на действительное число.
Согласованные матрицы. Умножение матриц и его свойства.
4.Элементарные преобразования матриц. Эквивалентные матрицы.
Элементарными преобразованиями матриц, явл.:
1)перестановка двух параллельных рядов матрицы
2)умножение всех элементов, любого ряда матрицы на отличное от нуля число
3)прибавление ко всем элементам ряда матриц соответствующих элемент.параллельного ряда и умноженное на одно и тоже число.
Две матрицы называются эквивалентными, если 1 из них получается из другой с помощью элементарных преобразований и обозначается А˜ В.
Определители 2-гопорядка.
n=2, A2×2= 
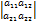
Определители 3-го порядка.
n=3, A= 
det A= 
Миноры и алгебраические дополнение элемента определителя.
Минором элемента aijопределителя порядка n называется определитель n-1-го порядка, полученный из исходного вычеркивания i-ой строки j-го столбца.
Алгебраическим дополнением элемента aijс определителем ∆наз. Соответствующие минором взятом i+j-числа, «+» если i+j-четна, «-» если i+j-нечетна.
Свойства определителей.
Свойства:
1)Определитель не изменится, если его строки заменить соответствующими столбцами и наоборот.
2)Если поменять местами два параллельных ряда определителя, то определитель изменит знак.
3)Определитель с двумя одинаковыми параллельными рядами равен 0.
4)Общий множитель, какого – либо ряда можно вынести за знак определителя.
5)Определитель, у которого элементы двух рядов соответственно пропорционален, то он =0.
6)Если все элементы какого-либо ряда определителя равны 0, то и сам определитель равен 0.
7)Определитель не изменится, если к элементам одного ряда прибавить соответственно элементы другого параллельного ряда, умножить на одно и то же число.
8)Определитель равен сумме произведения элементов любого ряда на их алгебраическое дополнение.
Свойства обратной матрицы.
Свойства:
Решение невырожденных систем линейных уравнений. Матричный метод. ФормулаКрамера. Метод Гаусса.
Матричный метод
Формула Крамера
Введём следующие обозначения:


т.е. определители ∆1, ∆2, ∆3, получаются из определителя ∆ путём замены его 1,2 и 3 столбцов соответственно столбцом свободных членов, тогда единственное решение системы может быть найдена по формуле Крамера: х1=∆1/∆, х2=∆2/∆, х3=∆3/∆.
Метод Гауса
С помощью элементарных преобразований над строками приведём матрицу к трапецеидальному виду:
Далее запишем систему линейных уравнений, которая соответствует расширенной матрице А :
из которых последовательно и найдём искомое решение.
Теорема Кронекера-Капелли
Проекция вектора на ось.
Осьюназ. всякая прямая, на которой указано направление.
Проекцией точки М на ось наз. основание перпендикуляра, опущенного из точки М на данную ось.
Углом между вектором ĀВ или равным ему вектором СВ и осью Ох наз. угол α, на который нужно повернуть кратчайшем образом полуось Ох, до совмещения её с вектором СВ.
Область изменения угла α: 0≤α≤π.
Проекцией вектора АВ на ось Ох наз. число, обозначаемое прОхАВ и /АВ/*cosα, где α- это угол между вектором Ав и осью Ох, т.е. по определению:
ПРОхАВ = /АВ/ * cosα
Теорема2.(u * v) ’ = u ’ v + uv ’
Правило Лопиталя.
Пусть функция f(x) и g(x) дифференцированны в окрестные точки Х0 и g ’ (x) 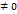
Если
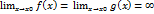


Замечание1.
Замечание2.Неопределённость вида 




Асимптоты графика функции.
Определение.ПрямаяL наз. асимптотойкривой y=f(x), если расстояние от точки M(x,y) кривой до прямой L стремится к нулю при неограниченном удалении этой точки по кривой от точки O(0;0) (т.е. при стремлении хотя бы одной из координат точки к ¥).
Асимптоты бывают вертикальные и невертикальные (наклонные и горизонтальные).
Утверждение 1. Прямая x=a явл. вертикальной асимптотой графика функции y=f(x), если
Т.е. для отыскания вертикальных асимптот нужно найти те значенияx, вблизи которых функция f(x) неограниченно возрастает по модулю.
Замечание 1. Если
D(y)=<(-¥;+¥) или [a;b] или (-¥;b] или [a;+¥)>, то вертикальных асимптот нет.
Замечание 2. Если
D(y)=(-¥;x1)È(x1;x2)È…È(xn;+¥), то вертикальные асимптоты могут быть только прямые.
(если 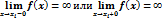
Замечание 3.Если D(y)=(a;+¥), то вертикальная асимптотой может быть только прямая x=a (если
Замечание 4.Если D(y)=(-¥;b), то вертикальной асимптотой может быть только прямая x=b (если
Утверждение 2. Если
то y=kx+b – невертикальная асимптота. Причем k¹0 – наклонная, а при k=0 – горизонтальная асимптота.
Первообразная функции. Неопределённый интеграл и его свойства. Таблица основных неопределённых интегралов.
Определение1. Функция F(x) наз. первообразной функции f(x), заданной на некотором множестве Х, если для любого х 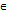
Определение2. Множество F(x) + C всех первообразной функции f(x) на множестве Х наз. неопределённым интегралом и обозначается:
Нахождение первообразной для данной функции f(x) наз. интегрированием функции f(x).
Теорема.Для всякой непрерывной на интервале (а,в) функции f(x) существует на этом промежутке первообразная, а значит и неопределённый интеграл.
Геометрический неопределённый интеграл представляет собой семейство кривых, зависимых от одного параметра С, который получает одна из другой путём параллельного сдвига вдоль оси Оу.
Свойства:
1)(
2)
3)
4)
5)Если
6)Если
Таблица основных неопределённых интегралов:
1.  x + C x + C | 6.  x dx = a x / ln a +C x dx = a x / ln a +C | 11.  |
2.  | 7.  | 12.  |
3.  = =  + C + C | 8.  | 13.  |
4.  = ln = ln  | 9. 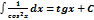 | 14.  |
5.  x dx = e x +C x dx = e x +C | 10.  | 15.  |
наз. однородным, если функция f(x,y) является функцией нулевого измерения.
Замечание 2.

67. Понятие функции двух переменных. Область определения.
Пусть каждой упорядоченной паре чисел (х, у) из некоторой области D соответствует определённое число zÎEÌR. Тогда z=f(x, y)наз. функцией двух переменныхх и у, х, у – независимыми переменными или аргументами, D – областью определения, а множествоЕ всех значений функции – областью её значений. Геометрически область определения функции z=f(x, y) представляет собой либо всю плоскость Оху, либо некоторую часть плоскости Оху ограниченную линиями, которые могут принадлежать или не принадлежать этой плоскости.
Линию, ограничивающую область наз. границей области. Точки области, не лежащие на границе наз. внутренними. Область состоящая только из одних внутренних точек наз. открытой. Область с присоединённой к ней границей наз. замкнутой, и обозначается 
Матрицы и их виды.
Матрица размером m*n –совокупность m*n чисел расположенных в виде таблицы.Из m-строк и n-столбцов.
— Матрица, все элементы, которой равны нулю наз. нулевой.
— Матрица, у которой число строк равно числу столбцов наз. квадратной.
— Квадратная матрица, у которой все элементы, кроме элемента главной диагонали равны нулю, наз. диагональной.
Диагональная матрица у которой каждый элемент =1, наз. единичной.
2.Сложение матриц и умножение на действительное число.
Согласованные матрицы. Умножение матриц и его свойства.
4.Элементарные преобразования матриц. Эквивалентные матрицы.
Элементарными преобразованиями матриц, явл.:
1)перестановка двух параллельных рядов матрицы
2)умножение всех элементов, любого ряда матрицы на отличное от нуля число
3)прибавление ко всем элементам ряда матриц соответствующих элемент.параллельного ряда и умноженное на одно и тоже число.
Две матрицы называются эквивалентными, если 1 из них получается из другой с помощью элементарных преобразований и обозначается А˜ В.
Определители 2-гопорядка.
n=2, A2×2= 
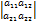
Определители 3-го порядка.
n=3, A= 
det A= 
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.
Умножение матриц. Согласованные матрицы



Матрицы
И действия над матрицами.
Матрица— прямоуг таблица чисел, содерж m-строк и n-столбцов.
1. Матрицы равны между собой, если равны соответств элементы этих матриц.
2. Матрица, в которой m=n наз квадратной или n-ого порядка.
3. Квадратная матрица, у которой все элементы, кроме элементов гл диагонали, равны 0 называется диагональной.
4. Диаг матрица, у которой каждый элемент главной диаг =1 наз единичной.
5. Квадратная матрица наз. треугольной, если все элементы, расположенные по одну сторону её гл диаг =0.
6. Матрица, у которой все числа, стоящие на гл диаг не нулевые, а также некоторое кол ненулевых строк, наз трапециевидной.
7. Матрица, содерж один столбец или строку, наз вектором из R n пространства.
Действия:
· Сложение – только для матриц одинакового размера.
· Умножение на вектор-столбец. Для умножения матрицы на вектор-столбец надо, чтобы число столбцов матрицы было равно числу координат вектора.
· Две матрицы наз эквивалентными, если одна из них получена из другой с помощью элементарным преобраз. любую матрицу можно привести к канонической.
Умножение матриц. Согласованные матрицы.
Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.
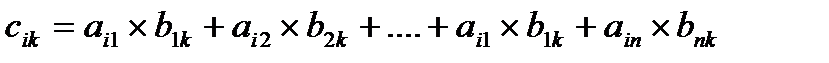
где i= 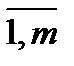
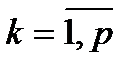
Матрицы А, n*m и В, m*n, назыв. согласованными. (если А согласованно с В, то это не значит, что В согласованно с А).
Смысл согласованности в том, чтобы количество столбцов 1-ой матрицы совпадало с количеством строк 2-ой матрицы. Для согласованных матриц можно определить операцию умножения.
Если матрицы A и B квадратные и одного размера, то A*B и B*A всегда существуют. Транспонированием называется смена всех элементов столбца соотв элементами строки. Если A T =A, то матрица А наз. симметричная(она обязательно квадратная).
Умножение матриц. Согласованные матрицы.
Умножение матриц. Согласованные матрицы.
Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.
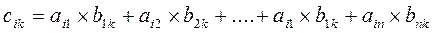
где i= 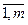
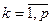
Матрицы А, n*m и В, m*n, назыв. согласованными. (если А согласованно с В, то это не значит, что В согласованно с А).
Смысл согласованности в том, чтобы количество столбцов 1-ой матрицы совпадало с количеством строк 2-ой матрицы. Для согласованных матриц можно определить операцию умножения.
Если матрицы A и B квадратные и одного размера, то A*B и B*A всегда существуют. Транспонированием называется смена всех элементов столбца соотв элементами строки. Если A T =A, то матрица А наз. симметричная(она обязательно квадратная).
Определителем матрицы А называется число:
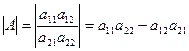
Матрица 3-его порядка:
Свойства определителей:
Замечание: АВ 
2.
3. пусть А = (аi,j) и при этом ее какой-либо ряд (либо столбец, либо строка) i-я строка обладает свойством, что:
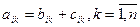

4. определитель равен нулю, если в нем есть нулевой ряд.
5. определитель = 0, если у него есть два одинаковых (пропорциональных) параллельных ряда.
6. определитель диагональной матрицы равен произведению элементов, стоящих на главной диагонали.
7. определитель треугольной матрицы равен произведению чисел, стоящих на главной диагонали.
8. если в определителях поменять местами, то определитель поменяет знак.
9. если к какому-то ряду определителя прибавить элементы другого параллельного ряда, умноженные на какое-то число (одинаковое), то определитель при этом не изменяется.
10. если какой-то ряд определителя содержит в себе обдщий множитель, то его можно вынести за знак определителя.
Теорема о разложении определителя. Теорема Лапласа.
Пусть есть определитель n-ого порядка. Зафиксируем число к: 1 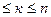
В исходном определителе вычеркнем к строк и к столбцов.
В результате такой операции все элементы определителя можно отнести к 3-ем разным типам:
2. 1 раз зачеркнутые
3. дважды зачеркнутые
Теперь из дважды зачеркнутых составим определитель. Такой определитель называется минором.
Теорема 1: ( о разложении определителя): Это теорема лапласа:
Алгоритм нахождения обратной матрицы:
аij 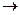
Теорема: (об аннулировании определителя):
сумма произведений элементов некоторого ряда определителя на алгебраическое дополнение к элементам другого параллельного ряда всегда равна нулю.
Невырожденные системы СЛАУ. Способы решения.
СЛАУ принято записывать в матричной форме, когда сами неизвестные не указываются, а указывается только матрица системы А и столбец свободных членов В.
Решение невырожденных СЛАУ методом Крамера:
X1= 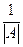
Теорема: (Крамера):
решение невырожденных уравнений АХ=В, 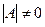
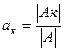
Прямая на плоскости.
Простейшей из линий является прямая. Разным способам задания прямой соответствует в прямоугольной система координат разные виды ее уравнений.
Пусть: tg 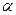
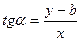
Число tg 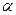
Плоскость в пространстве.
Простейшей поверхностью является плоскость. Плоскость в пространстве можно задавать различными способами. Каждому из них соответствует определенный вид ее уравнения.
1. Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору:
Точка Мо(Хо, Уо), вектор
2. Уравнение плоскости, проходящей через три данные точки:
3. Нормальное уравнение плоскости: 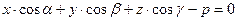
4. Угол между двумя плоскостями:
5. расстояние от точки до плоскости:
Прямая в пространстве.
1. Канонические уравнения прямой линии в пространстве, или уравнения прямой с направляющими коэффициентами, имеют вид:
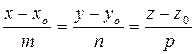
2. В параметрическом виде уравнения прямой линии в пространстве записываются так:
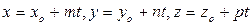
3. Общие уравнения прямой:
4. Векторное уравнение прямой:
5. уравнение прямой в пространстве, проходящей через две точки:
6. угол между прямыми:
Эллипс.
Геометрическое место точек, сумма расстояний от которых до двух фиксированных точек плоскости (обычно называемых фокусных) постоянна, называется эллипсом.
Если оси координат расположены так, что Ox проходит через фокусы F1(C,0) и F2(-C,0), а О(0,0) совпадает с серед отрезка F1F2, то по F1М+F2M получаем:
каноническое ур-ие эллипса 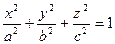
а и b- полуоси эллипса., а-большая, b-меньшая.
Эксцентриситет. 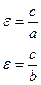
Эксцентриситет характеризует форму гиперболы: 
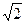
Директрисы – прямые 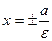
Фокальные радиусы: 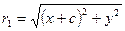
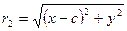
Есть гиперболы, которые имеют общие асимптоты. Такие гиперболы называются сопряженными.
Парабола.
Парабола – множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой.
Расстояние от фокуса до директрисы – параметр параболы (p>0).-полуфокальный диаметр.
Парабола есть линия второго порядка.
М(х,у) – произвольная точка параболы. Соединим точку М с F, проведем отрезок MN перпендикулярно директрисе. Согласно определению параболы MF=MN. По формуле расстояния между 2 точкам находим: 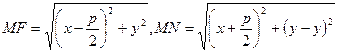
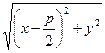
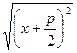
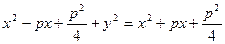
Каноническое уравнение параболы:
y 2 = 2px.
Эллипсоид.
Исследуем поверхность, заданную уравнением:
Рассмотрим сечения поверхности с плоскостями, параллельными плоскости xOy. Уравнения таких плоскостей: z=h,где h – любое число. Линия, получаемая в сечении, определяется двумя ур-ниями:
А) если 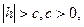
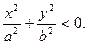
В) если 
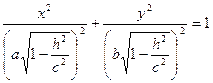
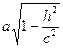
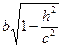
Рассмотренные сечения позволяют изобразить поверхность как замкнутую овальную поверхность. Поверхность называется эллипсоидами., если какие-либо полуоси равны, трехосный эллипсоид превращается в эллипсоид вращения, а если а=b=c, то в сферу.
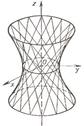
25. Гиперболоид и конус.
1. Исследуем поверхность 
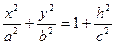
полуоси: а1= 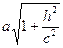
полуоси достигают своего наименьшего значения при h=0: а1=а, b1=b. При возрастании h полуоси эллипса будут увеличиваться. =>
Анализ этих сечений показывает, что поверхность, определяемая уравнением, имеет форму бесконечной расширяющейся трубки. Поверхность называется однополостным гиперболоидом.
2. 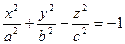
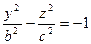
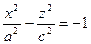
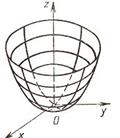
3. Конус второй степени
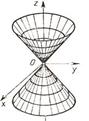
1. 
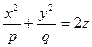
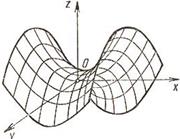
2. 
Цилиндрические поверхности.
Поверхность, образованная движением прямой L, которая перемещается в пространстве, сохраняя постоянное направление и пересекая каждый раз некоторую кривую K, называется цилиндрической поверхностью или цилиндром при этом кривая К – направляющая цилиндра, а L – его образующая.
Эллиптический цилиндр
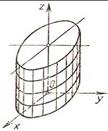
Уравнение: 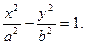
Все эти поверхности называются цилиндрами второго порядка, так как их уравнения есть уравнения второй степени относительно текущих координат x, y, z.
Полярная система координат.
Точка О называется полюсом, а луч l – полярной осью.
Суть задания какой- либо системы координат на плоскости состоит в том, чтобы каждой точке плоскости поставить в соответствие пару действительных чисел, определяющих положение этой точки на плоскости. В случае полярной системы координат роль этих чисел играют расстояние точки от полюса и угол между полярной осью и радиус– вектором этой точки. Этот угол j называется полярным углом.
Можно установить связь между полярной системой координат и декартовой прямоугольной системой, если поместить начало декартовой прямоугольной системы в полюс, а полярную ось направить вдоль положительного направления оси Ох.
Действительные числа.
Действительные числа образуют совокупность элементов, обладающую следующими свойствами.
1. a + b и ab (замкнутость),
2. a + b = b + a, ab = ba (коммутативность),
3. a + (b + c) = (a + b) + c = a + b + c, a(bc) = (ab)c = abc (ассоциативность
5. a(b + c) = ab + ac (дистрибутивность),
Действительное число 0 (нуль) обладает свойствами a + 0 = a, a * 0 = 0 для каждого действительного числа a.
Действительные числа, не являющиеся рациональными, называются иррациональными.
Предел последовательности.
Число а называется пределом последовательности, если для любого положительного числа Е найдется такое натуральное число N, что при всех n>N выполняется равенство:

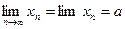
Коротко определение предела: 
Сходящаяся последовательность имеет только один предел. Последовательность, неимеющая предела, называется расходящейся.
Если 
Если 




34. Теоремы о пределах последовательности.
Теорема 1: (необходимый признак числовой последовательности):
Теорема Вейерштрасса: сформируем достаточный признак числовой последовательности: всякая ограниченная монотонная последовательность имеет предел.
Теорема : если две последовательности


Теорема: если 


Доказательство:
допустим, что а>b. Из равенств 











Предел функции.
Сформулируем два, эквивалентных между собой, определения предела функции в точке:
Коротко это определение:

Определение (по Гейне):
Число А называется пределом функции 


Односторонние пределы:
число А называется пределом функции 

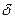
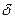



Предел слева записывают так:
Аналогично определяется предел функции справа:
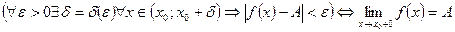
Пределы функции слева и справа называются односторонними пределами.
Предел функции при 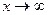
Число А называется пределом функции при 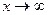




Односторонние пределы.
число А называется пределом функции 

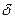
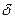



Предел слева записывают так:
Аналогично определяется предел функции справа:
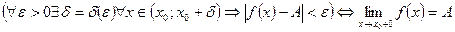
Пределы функции слева и справа называются односторонними пределами.
Сравнение бесконечно малых.
Две б.м.ф. сравниваются между собой с помощью их отношения:
1. если 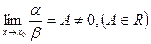
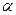
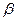
2. если 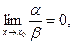
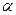
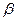
3. если 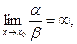
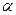
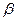
4. если 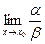
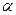
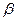
Таковы же правила сравнения б.м.ф. при 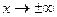
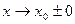
Эквивалентные бесконечно малые:
Теоремы о пределах.
Теорема: если существует 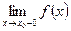
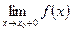
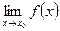
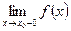
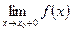
Теорема: если 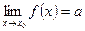
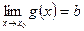
1)
2)
3)
Примечание 1: 1-е и 2-е свойства распространяются на любое конечное число слагаемых или сомножителей, однако число слагаемых и сомножителей не может быть 
Примечание 2:
Теорема: если 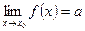

Следствие: если 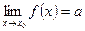

Теорема: если 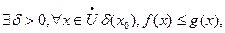
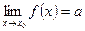
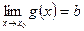
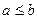
Теорема (о сжатой переменной): если 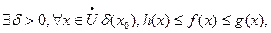
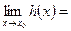
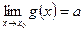
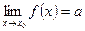
Теорема (о пределе сложной функции):
Пусть: х0, 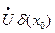
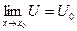
Сама теорема:
Если 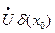
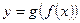
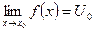
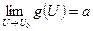
Дифференциал функции.
Пусть функция y = f(x) имеет производную в точке х:
Тогда можно записать: 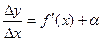
Следовательно: 
Величина aDx- бесконечно малая более высокого порядка, чем f¢(x)Dx, т.е. f¢(x)Dx- главная часть приращения Dу.
Определение. Дифференциалом функции f(x) в точке х называется главня линейная часть приращения функции.

Из определения следует, что dy = f¢(x)Dx или dy = f¢(x)dx.
Можно также записать:
Свойства дифференциала.
Если u = f(x) и v = g(x)- функции, дифференцируемые в точке х, то непосредственно из определения дифференциала следуют следующие свойства:
1) d(u ± v) = (u ± v)¢dx = u¢dx ± v¢dx = du ± dv
2) d(uv) = (uv)¢dx = (u¢v + v¢u)dx = vdu + udv
Доказательство.
( с учетом того, что если Dx®0, то Du®0, т.к. u = g(x) – непрерывная функция)
Тогда 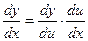
Умножение матриц. Согласованные матрицы.
Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.
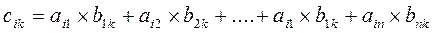
где i= 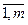
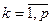
Матрицы А, n*m и В, m*n, назыв. согласованными. (если А согласованно с В, то это не значит, что В согласованно с А).
Смысл согласованности в том, чтобы количество столбцов 1-ой матрицы совпадало с количеством строк 2-ой матрицы. Для согласованных матриц можно определить операцию умножения.
Если матрицы A и B квадратные и одного размера, то A*B и B*A всегда существуют. Транспонированием называется смена всех элементов столбца соотв элементами строки. Если A T =A, то матрица А наз. симметричная(она обязательно квадратная).
Определителем матрицы А называется число:
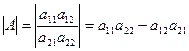
Матрица 3-его порядка:
Свойства определителей:
Замечание: АВ 
2.
3. пусть А = (аi,j) и при этом ее какой-либо ряд (либо столбец, либо строка) i-я строка обладает свойством, что:
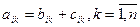

4. определитель равен нулю, если в нем есть нулевой ряд.
5. определитель = 0, если у него есть два одинаковых (пропорциональных) параллельных ряда.
6. определитель диагональной матрицы равен произведению элементов, стоящих на главной диагонали.
7. определитель треугольной матрицы равен произведению чисел, стоящих на главной диагонали.
8. если в определителях поменять местами, то определитель поменяет знак.
9. если к какому-то ряду определителя прибавить элементы другого параллельного ряда, умноженные на какое-то число (одинаковое), то определитель при этом не изменяется.
10. если какой-то ряд определителя содержит в себе обдщий множитель, то его можно вынести за знак определителя.