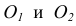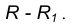Что такое сопряжение в черчении

Что такое сопряжение в черчении

§ 9. Сопряжения

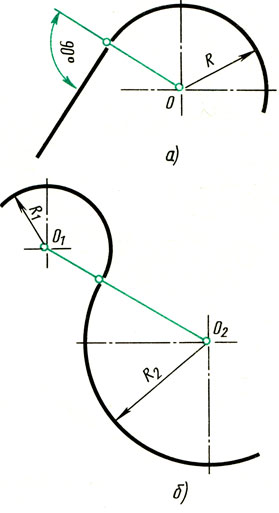
Плавный переход прямой линии в дугу или одной дуги в другую называют сопряжением. Для построения сопряжения надо найти центры, из которых проводят дуги, т. е. центры сопряжений (рис. 63). Затем нужно найти точки, в которых одна линия переходит в другую, т. е. точки сопряжений. При построении контура изображения сопрягающиеся линии нужно доводить точно до этих точек. Точка сопряжения лежит на перпендикуляре, опущенном из центра О дуги на сопрягаемую прямую (рис. 64, а), или на линии О₁О₂, соединяющей центры сопрягаемых дуг (рис. 64, б). Следовательно, для построения любого сопряжения дугой заданного радиуса нужно найти центр сопряжения и точку сопряжения.

Рис. 63. Элементы сопряжений

Рис. 64. Определение точки сопряжения

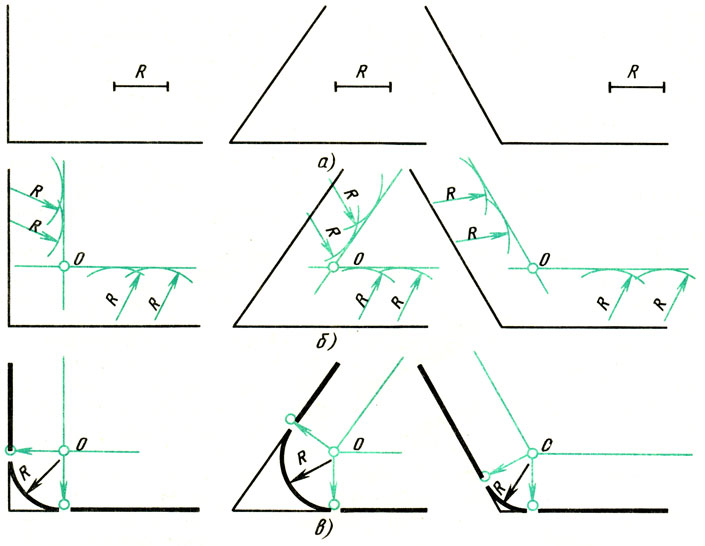
Сопряжение двух пересекающихся прямых дугой заданного радиуса. Даны пересекающиеся под прямым, острым и тупым углами прямые линии (рис. 65, а). Нужно построить сопряжения этих прямых дугой заданного радиуса R.

Для всех трех случаев применяют общий способ построения.

Для построения прямых, параллельных сторонам угла, из произвольных точек, взятых на прямых, раствором циркуля, равным R, делают засечки и к ним проводят касательные.

2. Находят точки сопряжений (рис. 65, в). Для этого опускают перпендикуляры из точки О на заданные прямые.

3. Из точки О, как из центра, описывают дугу заданного радиуса R между точками сопряжений (рис. 65, в).

Рис. 65. Сопряжение двух пересекающихся прямых

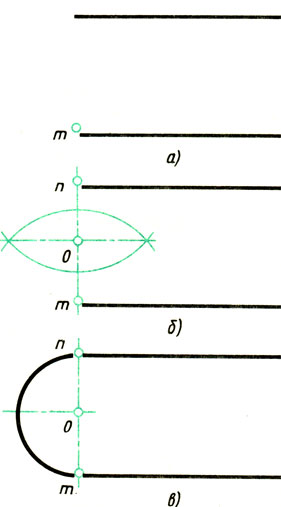
Сопряжение двух параллельных прямых. Заданы две параллельные прямые и на одной из них точка сопряжения т (рис. 66, а). Требуется построить сопряжение.

Построение выполняют следующим образом:

1. Находят центр сопряжения и радиус дуги (рис. 66, б). Для этого из точки m на одной прямой восставляют перпендикуляр до пересечения с другой прямой в точке п. Отрезок делят пополам (см. рис. 56).

Рис. 66. Сопряжение двух параллельных прямых

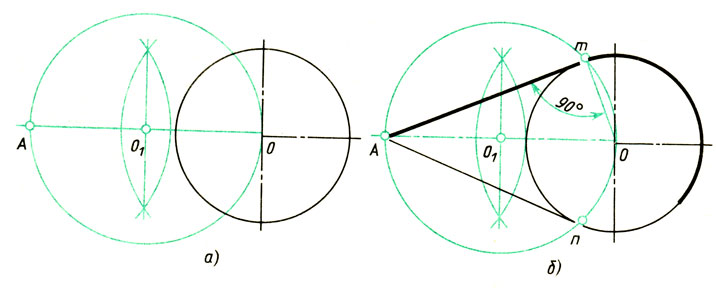
Проведение касательной к окружности. Задана окружность с центром О и точка А (рис. 67, а). Требуется провести из точки А касательную к окружности.

1. Точку А соединяют прямой с заданным центром О окружности.

Строят вспомогательную окружность диаметром, равным ОА (рис. 67, а). Чтобы найти центр О₁ делят отрезок ОА пополам (см. рис. 56).

Рис. 67. Построение касательной к двум окружностям

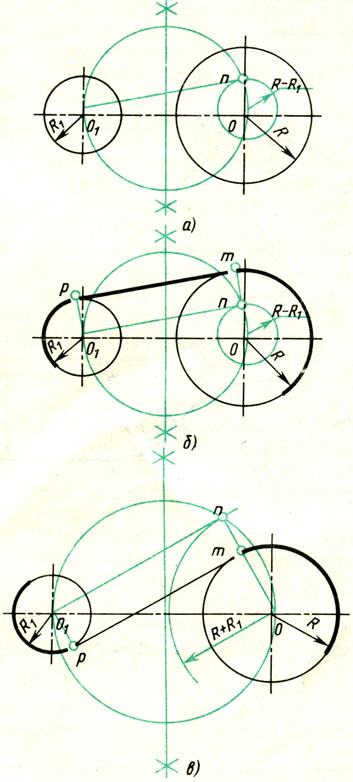
Проведение прямой, касательной к двум окружностям. Заданы две окружности радиусом R и R₁. Требуется построить касательную к ним.

Различают два случая касания: внешнее (рис. 68, б) и внутреннее (рис. 68, в).

При внешнем касании построение выполняют следующим образом:

2. Радиус, проведенный из точки О в точку n, продолжают до пересечения в точке m с заданной окружностью радиусом R. Параллельно радиусу Оm проводят радиус 0₁р меньшей окружности. Прямая, соединяющая точки сопряжений m и р,- касательная к заданным окружностям (рис. 68, б).

При внутреннем касании построение проводят аналогично, но вспомогательную окружность проводят радиусом, равным сумме радиусов R + R₁ (см. рис. 68, в). Затем из центра O₁ проводят касательную к вспомогательной окружности (см. рис. 67). Точку n соединяют радиусом с центром О. Параллельно радиусу On проводят радиус O₁р меньшей окружности. Искомая касательная проходит через точки сопряжений m и р.

Рис. 68. Построение касательной к окружности

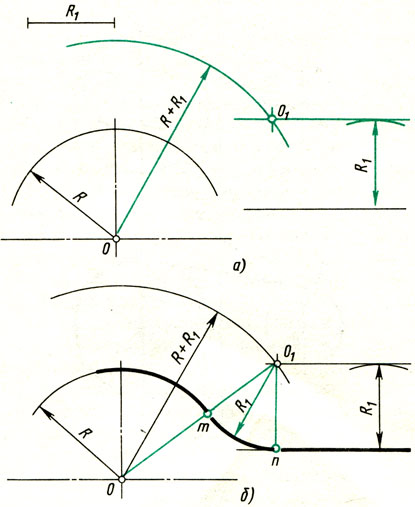
Сопряжение дуги и прямой линии дугой заданного радиуса. Заданы дуга окружности радиусом R и прямая. Требуется соединить их дугой радиусом R₁.

1. Находят центр сопряжения (рис. 69, а), который должен находиться на расстоянии R₁ от дуги и от прямой. Такому условию соответствует точка пересечения прямой линии, параллельной заданной прямой, проходящей от нее на расстоянии R₁, и вспомогательной дуги, отстоящей от заданной также на расстоянии R₁. Поэтому проводят вспомогательную прямую, параллельную заданной прямой, на расстоянии, равном радиусу сопрягающей дуги R₁ (рис. 69, а). Раствором циркуля, равным сумме заданных радиусов R + R₁, описывают из центра О дугу до пересечения с вспомогательной прямой. Полученная точка O₁— центр сопряжения.

2. По общему правилу находят точки сопряжения (рис. 69, б). Соединяют прямой центры сопрягаемых дуг O₁ и О. Опускают из центра сопряжения O₁ перпендикуляр на заданную прямую.

3. Из центра сопряжения O₁ между точками сопряжения m и n проводят дугу, радиус которой равен R 1 (см. рис. 69, б).

Рис. 69. Сопряжение дуги окружности и прямой

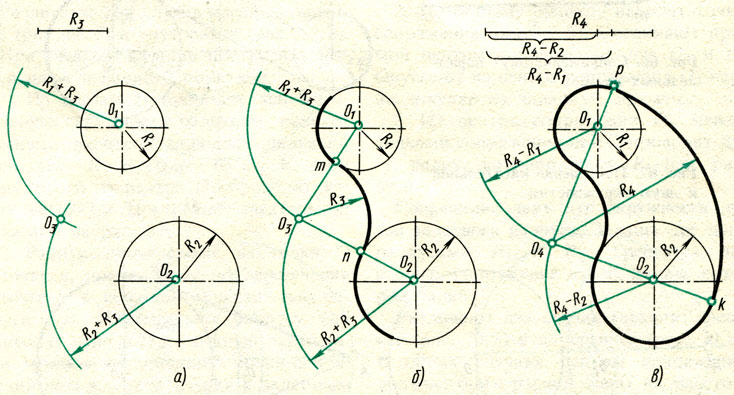
Сопряжение двух дуг окружности дугой заданного радиуса. Заданы две дуги радиусами R₁ и R₂. Требуется построить сопряжение дугой, радиус которой задан.

Различают два случая касания: внешнее (рис. 70, б) и внутреннее (рис. 70, в). В обоих случаях центры сопряжений должны быгь расположены на расстоянии, равном радиусу дуги сопряжения, от заданных дуг. По общему правилу на прямых, соединяющих центры сопрягаемых дуг, находят точки сопряжения.

Ниже приведен порядок построения для внешнего и внутреннего касаний.

2. Соединив прямыми точку O₁ с точкой O₃ и точку O₂ с точкой O₃, находят точки сопряжения m и n (см. рис. 70, б),

3. Из точки О₃ раствором циркуля, равным R₃, между точками m и n описывают сопрягающую дугу.

Для внутреннего касания выполняют те же построения, но радиусы дуг берут равными разности радиусов сопрягающей и заданной дуг, т.е. R₄-R₁ и R₄-R₂. Точки сопряжения р и k лежат на продолжении линий, соединяющих точку О₄ с точками O₁ и O₂.

Рис. 70. Сопряжение двух дуг окружности

Источник

Сопряжения в инженерной графике на чертежах с примерами

Содержание:

В очертаниях технических форм часто встречаются плавные переходы от од- ной линии к другой. Плавный переход одной линии в другую, выполненный при помощи промежуточной линии, называется сопряжением. Построение сопряжений основано на следующих положениях геометрии.

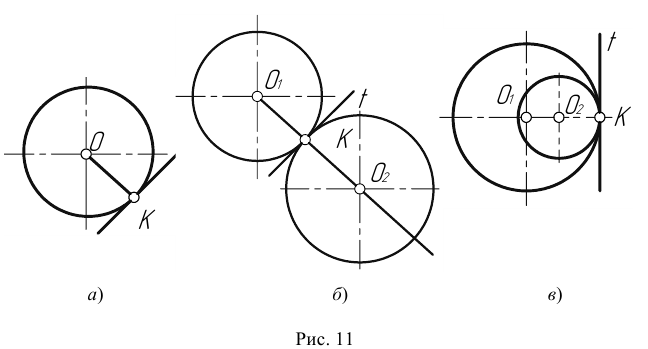
Точка касания К и центры окружностей

Для выполнения сопряжений необходимо определить три элемента построения: 1) радиус сопряжения; 2) центр сопряжения; 3) точки сопряжения.

Сопряжение двух пересекающихся прямых линий

Пусть даны две пересекающиеся прямые m, n и радиус сопряжения R (рис. 12). Необходимо построить сопряжение данных прямых дугой окружности радиусом R.

Выполним следующие построения:

Проведем дугу сопряжения AB. Теперь будут определены все элементы сопряжения: радиус, центр и точки сопряжения.

Сопряжения прямой с окружностью

Сопряжение прямой с окружностью может быть внешним или внутренним. Рассмотрим построение внешнего сопряжения прямой с окружностью.

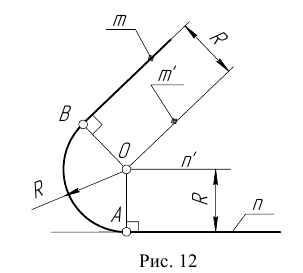
Пример 1. Пусть задана окружность радиусом R с центром в точке 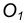и прямая m. Требуется построить сопряжение окружности с прямой дугой окружности заданного радиуса R (рис. 13).

Для решения задачи выполним следующие построения:

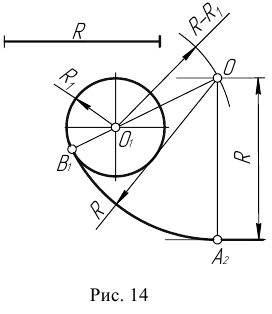
Пример 2. При построении внутреннего сопряжения (рис. 14) последовательность построений остается та же, что и в примере 1. Однако центр сопряжения определяется с помощью вспомогательной дуги окружности, проведенной из центра 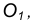, радиусом

Сопряжение двух окружностей

Сопряжение двух окружностей может быть внешним, внутренним и смешанным. Пусть задан радиус сопряжения R, а центры сопряжения и точки сопряжения следует найти.

Пример 1. Построим сопряжение с внешним касанием двух данных окружностей m и n с радиусами 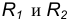дугой заданного радиуса R (рис. 15а).

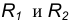
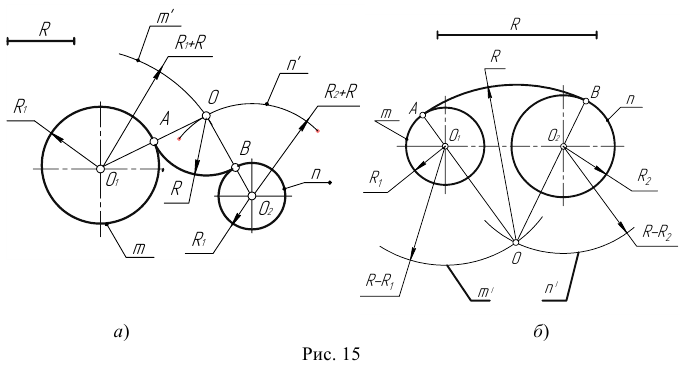
Пример 2. Построим сопряжение с внутренним касанием двух данных окружностей m и n с радиусами дугой радиусом R (рис. 15б).

Пример 3. На рис. 16 приведен пример построения сопряжения с внешне- внутренним касанием.

Построение касательных

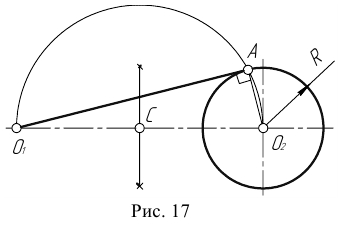
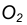
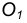
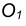
Пример 1. Дана окружность с центром в точке и точка вне её. Через данную точку провести касательную к данной окружности (рис. 17).

Для решения задачи выполним следующие построения.

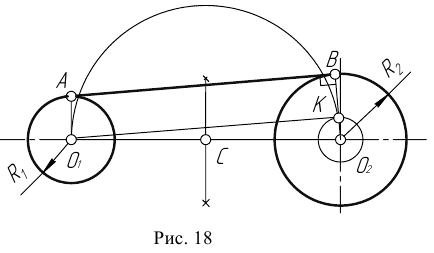
Пример 2. Построим общую касательную АВ к двум заданным окружностям радиусов 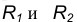(рис. 18).

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Сопряжения

В этой небольшой статье, будут рассмотрены основные виды сопряжений и Вы узнаете о том, как построить сопряжение углов, прямых линий, окружностей и дуг, окружностей с прямой.

Сопряжением называют плавный переход одной линии в другую. Для того чтобы построить сопряжение, нужно найти центр сопряжения и точки сопряжений.

Точка сопряжения – это общая точка для сопрягаемых линий. Точку сопряжения также называют точкой перехода.

Ниже будут рассмотрены основные типы сопряжений.

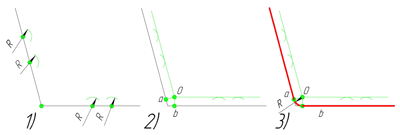
Сопряжение углов (Сопряжение пересекающихся прямых)

Сопряжение прямого угла(Сопряжение пересекающихся прямых под прямым углом)

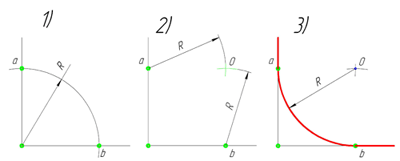
В данном примере будет рассмотрено построение сопряжения прямого угла заданным радиусом сопряжения R. Первым делом найдём точки сопряжения. Для нахождения точек сопряжения, нужно поставить циркуль в вершину прямого угла и провести дугу радиусом R до пересечения со сторонами угла. Полученные точки и будут являться точками сопряжения. Далее нужно найти центр сопряжения. Центром сопряжения будет точка равноудалённая от сторон угла. Проведём из точек a и b две дуги радиусом сопряжения R до пересечения друг с другом. Полученная на пересечении точка О и будет центром сопряжения. Теперь из центра сопряжения точки О описываем дугу радиусом сопряжения R от точки a до точки b. Сопряжение прямого угла построено.

Сопряжение острого угла(Сопряжение пересекающихся прямых под острым углом)

Ещё один пример сопряжения угла. В этом примере будет построено сопряжение
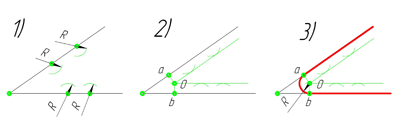
острого угла. Для построения сопряжения острого угла раствором циркуля,равным радиусу сопряжения R, проведём из двух произвольных точек на каждой стороне угла по две дуги. Затем проведём касательные к дугам до пересечения в точке О, центре сопряжения. Из полученного центра сопряжения опустим перпендикуляр к каждой из сторон угла. Так мы получим точки сопряжения a и b. Затем проведём из центра сопряжения, точки О, дугу радиусом сопряжения R, соединив точки сопряжения a
и b. Сопряжение острого угла построено.

Сопряжение тупого угла(Сопряжение пересекающихся прямых под тупым углом)

Сопряжение тупого угла строится по аналогии с сопряжением острого угла. Мы также, сначала радиусом сопряжения R проводим по две дуги из двух произвольно взятых точек на каждой из сторон, а затем проводим касательные к этим дугам до пересечения в точке О, центре сопряжения. Затем опускаем перпендикуляры из центра сопряжения к каждой из сторон и соединяем дугой, равной радиусу сопряжения тупого угла R, полученные точки a и b.

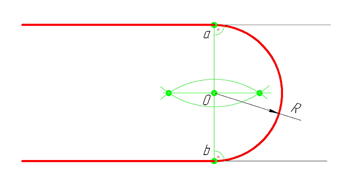
Сопряжение параллельных прямых линий

Построим сопряжение двух параллельных прямых. Нам задана точка сопряжения a, лежащая на одной прямой. Из точки a проведём перпендикуляр до пересечения его с другой прямой в точке b. Точки a и b являются точками сопряжения прямых линий. Проведя из каждой точки дугу, радиусом больш отрезка ab, найдём центр сопряжения — точку О. Из центра сопряжения проведём дугу заданного радиуса сопряжения R.

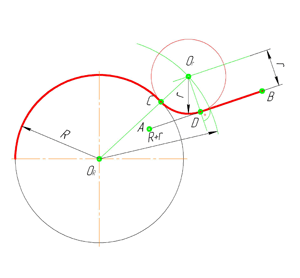
Сопряжение окружностей(дуг) с прямой линией

Внешнее сопряжение дуги и прямой линии

В этом примере будет построено сопряжение заданным радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиусом R.

Внутреннее сопряжение прямой линии с дугой

Из центра сопряжения(точка О r ) опустим перпендикуляр на прямую AB. Точка D, полученная на основании перпендикуляра, и будет точкой сопряжения.

Сопряжение окружностей (дуг)

Внешнее сопряжение дуг окружностей

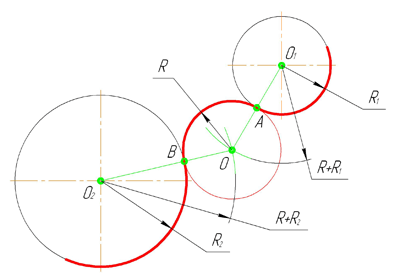
Внешним сопряжением считается сопряжение, при котором центры сопрягаемых окружностей(дуг) O1( радиус R1) и O2 (радиус R2) располагаются за сопрягающей дугой радиуса R. На примере рассмотрено внешнее сопряжение дуг. Сначала находим центр сопряжения. Центром сопряжения является точка пересечения дуг окружностей с радиусами R+R1 и R+R2, построенных из центров окружностей O1(R1) и O2(R2) соответственно. Затем центры окружностей O1 и O2 соединяем прямыми с центром сопряжения, точкой O, и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. После этого, из центра сопряжения строим дугу заданного радиуса сопряжения R и соединяем ей точки A и B.

Внутреннее сопряжение дуг окружностей

Внутренним сопряжением называется сопряжение, при котором центры сопрягаемых дуг O1, радиуса R1, и O2, радиус R2, располагаются внутри сопрягающей их дуги заданного радиуса R. На картинке ниже приведён пример построения внутреннего сопряжения окружностей(дуг). Вначале мы находим центр сопряжения, которым является точка O, точка пересечения дуг окружностей с радиусами R-R1 и R-R2 проведённых из центров окружностей O1и O2 соответственно. После чего соединяем центры окружностей O1 и O2 прямыми линиями с центром сопряжения и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. Затем из центра сопряжения строим дугу сопряжения радиуса R и строим сопряжение.

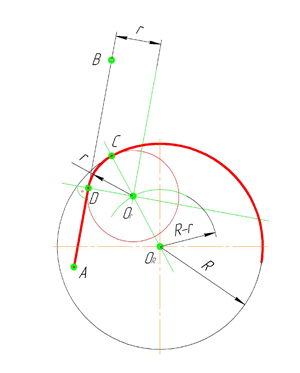
Смешанное сопряжение дуг окружностей

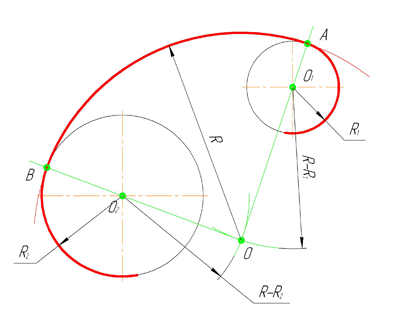
Смешанным сопряжением дуг является сопряжение, при котором центр одной из сопрягаемых дуг (O1) лежит за пределами сопрягающей их дуги радиуса R, а центр другой окружности(O2) – внутри её. На иллюстрации ниже приведён пример смешанного сопряжения окружностей. Сначала находим центр сопряжения, точку O. Для нахождения центра сопряжения строим дуги окружностей с радиусами R+R1, из центра окружности радиуса R1 точки O1, и R-R2, из центра окружности радиуса R2 точки O2. После чего соединяем центр сопряжения точку O с центрами окружностей O1 и O2 прямыми и на пересечении с линиями соответствующих окружностей получаем точки сопряжения A и B. Затем строим сопряжение.

Источник

Что такое сопряжение в черчении

При вычерчивании деталей машин и приборов, кон­туры очертаний которых состоят из прямых линий и дуг окружностей с плавными переходами от одной линии в другую, часто применяют сопряжения. Сопря­жением называется плавный переход одной линии в другую. На рис. 60 показаны примеры применения сопряжений.

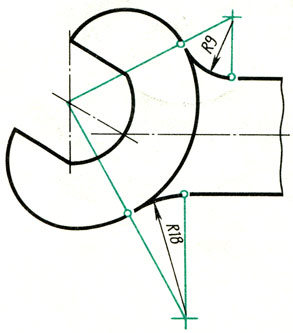
Контур рычага (рис. 60а) состоит из отдельных линий, плавно переходящих одна в другую, например, в точках А, А₁ виден плавный переход от дуги окруж­ности к прямой линии, а в точках В, В₁ — от дуги одной окружности к дуге другой окружности (рис. 60, б). На рис. 60, в изображен двурогий крюк. На чертеже кон­тура крюка (рис. 60, г) в точке А виден плавный пере­ход от дуги окружности D=200 к прямой линии, а в точке В — от дуги окружности радиуса R460 к дуге ра­диуса R260.

Для точного и правильного выполнения чертежей необходимо уметь выполнять построения сопряжений, которые основаны на двух положениях.

СОПРЯЖЕНИЕ ДВУХ СТОРОН УГЛА ДУГОЙ ОКРУЖНОСТИ ЗАДАННОГО РАДИУСА

При выполнении чертежей деталей, показанных на рис. 62, б, г, е, выполняют построение сопряжения двух сторон угла дугой окружности заданного радиуса. На рис. 62, а выполнено построение сопряжения сто­рон острого угла дугой, на рис. 62, в — тупого угла, на рис. 62, д — прямого.

Сопряжение двух сторон угла (острого или тупого) дугой заданного радиуса R выполняют следующим образом (рис. 62, а и в).

Параллельно сторонам угла на расстоянии, равном радиусу дуги R, проводят две вспомогательные прямые линии. Точка пересечения этих прямых (точка О) будет центром дуги радиуса Я, т. е. центром сопряже­ния. Из центра О описывают дугу, плавно переходя­щую в прямые — стороны угла. Дугу заканчивают в точках сопряжения n и n₁ которые являются Основаниями перпендикуляров, опущенных из центра О на сто­роны угла.

СОПРЯЖЕНИЕ ПРЯМОЙ С ДУГОЙ ОКРУЖНОСТИ

Сопряжение прямой с дугой окружности может быть выполнено при помощи дуги с внутренним касанием (рис. 63, в) и дуги с внешним касанием (рис. 63, а).

На рис. 63, а показано сопряжение дуги окружности радиусом R и прямой линии А В дугой окружности радиуса r с внешним касанием. Для построения такого сопряжения проводят окружность радиуса R и прямую АВ. Параллельно заданной прямой на расстоянии, рав­ном радиусу r (радиус сопрягающей дуги), проводят прямую ab. Из центра О проводят дугу окружности

радиусом, равным сумме радиусов и r, до пересече­ния ее с прямой ab в точке О₁ Точка О₁ является цент­ром дуги сопряжения.

Точку сопряжения с находят на пересечении прямой 00 ₁ с дугой окружности радиуса R. Точка сопряжения C₁ является основанием перпендикуляра, опущенного из центра О₁ на данную прямую При помощи ана­логичных построений могут быть найдены точки 0₂,

На рис. 63, б показан кронштейн, при вычерчивании контура которого необходимо выполнить построения, описанные выше.

На рис. 63, в выполнено сопряжение дуги радиуса R с прямой А В дугой радиуса r с внутренним касанием. Центр дуги сопряжения О₁ находится на пересечении вспомогательной прямой, проведенной параллельно данной прямой на расстоянии r, с дугой вспомогатель­ной окружности, описанной из центра О радиусом, рав­ным разности R—r. Точка сопряжения является основанием перпендикуляра, опущенного из точки О₁ на данную прямую. Точку сопряжения с находят на пересечении прямой ОО₁ с сопрягаемой дугой. Такое сопряжение выполняют, например, при вычерчивании контура маховика, показанного на рис. 63, г.

СОПРЯЖЕНИЕ ДУГИ С ДУГОЙ

Сопряжение двух дуг окружностей может быть вну­тренним, внешним и смешанным.

При внутреннем сопряжении центры O и O₁ сопря­гаемых дуг находятся внутри сопрягающей дуги ради­уса R (рис. 64, б).

При внешнем сопряжении центры и сопрягае­мых дуг радиусов R₁ и R₂ находятся вне сопрягающей дуги радиуса R (рис. 64, в).

При смешанном сопряжении центр О, одной из сопрягаемых дуг лежит внутри сопрягающей дуги

радиуса R, а центр О другой сопрягаемой дуги вне ее (рис. 65, а).

На рис. 64, а показана деталь (серьга), при вычерчи­вании которой необходимо построение внутреннего и внешнего сопряжения.

Построение внутреннего сопряжения.

а) радиусы сопрягаемых окружностей R₁ и R₂

б) расстояния l₁ и l₂ между центрами этих дуг;

в) радиус R сопрягающей дуги.

а) определить положение центра 0₂ сопрягающей дуги;

б) найти точки сопряжения s₁ и s

в) провести дугу сопряжения.

Построение сопряжения показано на рис. 64, б. По заданным расстояниям между центрами 1₁ и l₂ на чер­теже намечают центры О и O₁ из которых описывают сопрягаемые дуги радиусов R₁ и R₂. Из центра О₁ про­водят вспомогательную дугу окружности радиусом, равным разности радиусов сопрягающей дуги R и сопрягаемой R₂, а из центра О — радиусом, равным разности радиусов сопрягающей дуги R и сопрягаемой R₁ Вспомогательные дуги пересекутся в точке 0₂ которая и будет искомым центром сопрягающей дуги.

Для нахождения точек сопряжения точку 0₂ соеди­няют с точками О и О₁ прямыми линиями. Точки пере­сечения продолжения прямых 0₂0 и 0₂0 с сопрягае­мыми дугами являются искомыми точками сопряжения (точки S и s₁).

Радиусом R из центра О_г проводят сопрягающую дугу между точками сопряжения s и s₁

Построение внешнего сопряжения.

б) расстояния и l₂ между центрами этих дуг;

в) радиус R сопрягающей дуги.

а) определить положение центра 0₂ сопрягающей дуги;

б) найти точки сопряжения и s₁;

в) провести дугу сопряжения.

Построение внешнего сопряжения показано на рис. 64, в. По заданным расстояниям между центрами l₁ и l₂ на чертеже находят точки О и О₁ из которых описывают сопрягаемые дуги радиусов R₁ и R₂. Из центра О проводят вспомогательную дугу окружности радиусом, равным сумме радиусов сопрягаемой дуги R₁, и сопряга­ющей R, а из центра О₁ — радиусом, равным сумме

радиусов сопрягаемой дуги R₂ и сопрягающей R. Вспо­могательные дуги пересекутся в точке O₂, которая будет искомым центром сопрягающей дуги Для нахождения точек сопряжения центры дуг сое-

диняют прямыми линиями 00₂ и 010₂. Эти две пря­мые пересекают сопрягаемые дуги в точках сопряже­ния S и s1

Из центра 0₂ радиусом R проводят сопрягающую ду­гу, ограничивая ее точками сопряжения и

Построение смешанного сопряжения. Пример сме­шанного сопряжения приведен на рис. 65, и где изображены кронштейн и его чертеж.

б) расстояния l₁ и l₂ между центрами этих дуг;

в) радиус R сопрягающей дуги.

а) определить положение центра 0₂ сопрягающей дуги;

б) найти точки сопряжения s и s₁

в) провести дугу сопряжения.

По заданным расстояниям между центрами l₁ и l₂ на чертеже намечают центры 0 и 0₁, из которых описы­вают сопрягаемые дуги радиусов R₁ и R₂. Из центра О проводят вспомогательную дугу окружности радиусом, равным сумме радиусов сопрягаемой дуги R₁ и сопрягающей R, а из центра 0₁ — радиусом, равным разности радиусов R и R₂. Вспомогательные дуги пересекутся в точке 0₂, которая будет искомым центром сопряга­ющей дуги.

Соединив точки О и 0₂ прямой, получают точку сопряжения соединив точки О₁ и 0₂, находят точку сопряжения s. Из центра 0₂ проводят дугу сопряжения от s до s₁

При вычерчивании контура детали необходимо разо­браться, где имеются плавные переходы, и предста­вить себе, где надо выполнить те или иные виды сопря­жения.

Для приобретения навыков построения сопряжения выполняют упражнения по вычерчиванию контуров сложных деталей. Перед упражнением необходимо просмотреть задание, наметить порядок построения сопряжений и только после этого приступить к выпол­нению построений.

На рис. 66, а изображена деталь (кронштейн), а на рис. 66, б, в, г показана последовательность выполне­ния контурного очертания этой детали с построением различных видов сопряжений.

Источник