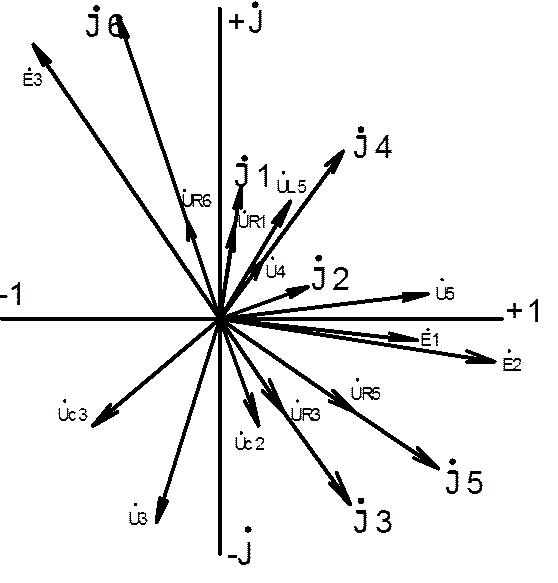Что такое сопряженный ток
3.4 Комплексная форма записи мощности
Допустим, что через электрическую цепь проходит гармонический ток, причем положительные направления тока и напряжения на зажимах цепи приняты совпадающими (рисунок 3.8).
Комплексные действующие значения тока и напряжения равны соответственно:
Фазовый сдвиг тока относительно напряжения равен разности начальных фаз
Умножим 


Отсюда следует, что
Так как напряжение может рассматриваться как сумма активной и реактивной слагающих:

Аналогично мощность может быть выражена через активный и реактивный токи.
Таким образом, комплексная величина 
Модуль S равен полной мощности. 
На комплексной плоскости 
Треугольник мощностей, изображенный на рисунке 3.9, подобен треугольнику сопротивлений

Поэтому мощности Р и Q на зажимах цепи могут быть записаны в следующем виде
Воспользовавшись выражением (2.28), получим
Эта формула справедлива при любой схеме соединений индуктивности, емкости и сопротивлений.
Энергетический метод определения комплексного сопротивления применим и к комплексной проводимости
откуда 
где 
Итак, активные сопротивление и проводимость цепи зависят от поглощаемой цепью активной мощности, а реактивные сопротивление и проводимость – от разности максимальных значений энергии, запасаемых в магнитном и электрическом полях.
СОПРЯЖЕННЫЙ
СОПРЯЖЁННЫЙ сопряжённая, сопряжённое; сопряжён, сопряжена, сопряжено (книжн.). 1. Прич. страд. прош. вр. от сопрячь (устар.). || с чем. Неразрывно связанный, соединенный с чем-н., такой, чему непременно сопутствует что-н. другое. Это сопряжено с большими затруднениями. Путь, сопряжённый с опасностью. 2. Взаимно связанный, находящийся во взаимодействии (спец.). Сопряженные точки (точки в оптической системе, находящиеся в таком соотношении, что если предмет поместить в одной из них, что его изображение получится в другой; физ.). Сопряженные рессоры (тех.).
Смотреть что такое СОПРЯЖЕННЫЙ в других словарях:
СОПРЯЖЕННЫЙ
сопряжённый прил. Неразрывно связанный с чем-л., такой, которому непременно сопутствует что-л. другое.
СОПРЯЖЕННЫЙ
сопряжённый 1. (с тв.) attended (by) это сопряжено с большими затруднениями — that will entail great difficulties 2. мат., физ., тех. conjugate сопря. смотреть
СОПРЯЖЕННЫЙ
СОПРЯЖЕННЫЙ
сопряженный прил. (12)мн.им.Не почести, с этим сопряженные: это дым, мечтаСтуд. 1.5.Праздность, роскошь, не сопряженные ни с малейшим чувствомПс12.мн.р. смотреть
СОПРЯЖЕННЫЙ
1) (с чем-либо) lié à qch, joint à qch, uni à qch это сопряжено с большими затруднениями — cela offre de grandes difficultés2) мат., физ., тех. conjugu. смотреть
СОПРЯЖЕННЫЙ
1) <math.> adjoint2) conjugate3) conjugated4) coupled– комплексно сопряженный– процесс сопряженный– сопряженный дальномер– сопряженный импульс– с. смотреть
СОПРЯЖЕННЫЙ
СОПРЯЖЕННЫЙ
сопряжённыйспц(связанный) conjugado; conexoСинонимы: комплексный, конъюгированный, координированный, неотчуждаемый, неотъемлемый, связанный, скоордини. смотреть
СОПРЯЖЕННЫЙ
прил. 1) legato, unito это сопряжено с большими трудностями — ciaò è legato a grandi difficoltà это сопряжено с большими расходами — ciò comporta grosse spese 2) сопряженные углы мат. — angoli consecutivi Итальяно-русский словарь.2003. Синонимы: комплексный, конъюгированный, координированный, неотчуждаемый, неотъемлемый, связанный, скоординированный, соединенный, сочлененный. смотреть
СОПРЯЖЕННЫЙ
(с чем-либо) verknüpft, verbunden (связанный); тех. gekoppeltСинонимы: комплексный, конъюгированный, координированный, неотчуждаемый, неотъемлемый, св. смотреть
СОПРЯЖЕННЫЙ
• konjugovaný• on-line přístup• přiléhající• přiřazený (ozubené kolo)• sdružený• spoluzabírající• spražený režim• spražený režim (on-line)
СОПРЯЖЕННЫЙ
страд. прич., прош. вр.Краткая форма: сопряженот глагола: сопрячьсполучений
СОПРЯЖЕННЫЙ
• неразрывно сопряженныйСинонимы: комплексный, конъюгированный, координированный, неотчуждаемый, неотъемлемый, связанный, скоординированный, соединенн. смотреть
СОПРЯЖЕННЫЙ
сопряжённый = 1. (с тв.; связанный ) attended (by); сопряжённый дальномер тех. coupled range finder; это сопряжено с большими затруднениями that wilI entail great difficulties; 2. мат., хим. conjugate; тех. coupled, connected.
СОПРЯЖЕННЫЙ
1. seostatud2. seostunud3. seotud4. ühend-5. ühendatud
СОПРЯЖЕННЫЙ
сопряж||енный1. прич. от сопрягать· 2. прил (с чем-л.) συνδεδεμένος: это дело
ено с затруднениями ἡ ὑπόθεση αὐτή συνεπάγεται (или συνεπιφέρει) πολλές δυσκολίες· 3. прил мат, физ. συζυγής. смотреть
СОПРЯЖЕННЫЙ
СОПРЯЖЕННЫЙ
adjungiert, (о реакции) gekoppelt, (о связях) konjugiert
СОПРЯЖЕННЫЙ
СОПРЯЖЕННЫЙ
abgeglichen эл.; радио, konjugiert
СОПРЯЖЕННЫЙ
сопряженный принадлежащий, сочлененный, соединенный, комплексный, связанный, конъюгированный, координированный, скоординированный
СОПРЯЖЕННЫЙ
СОПРЯЖЕННЫЙ прилагательное Неразрывно связанный с чем-либо, такой, которому непременно сопутствует что-либо другое.
сопряжённый ток
Смотреть что такое «сопряжённый ток» в других словарях:
ЗАРЯЖЕННЫЙ ТОК — ток в квант. теории поля, изменяющий на единицу электрич. заряды ч ц (в отличие от нейтрального тока, не меняющего заряды). З. т. входит в лагранжиан слабого взаимодействия и состоит из лептонной и адронной частей. Напр., b распад нейтрона n® p+e … Физическая энциклопедия
Слабые взаимодействия — один из четырёх типов известных фундаментальных взаимодействий между элементарными частицами (три других типа электромагнитное, гравитационное и сильное). С. в. гораздо слабее не только сильного, но и электромагнитного взаимодействий, но… … Большая советская энциклопедия
СЛАБОЕ ВЗАИМОДЕЙСТВИЕ — одно из четырёх известных фундам, вз ствий между элем. ч цами. С. в. гораздо слабее не только сильного, но и эл. магн. вз ствия, но гораздо сильнее гравитационного. О силе вз ствия можно судить по скорости процессов, к рые оно вызывает. Обычно… … Физическая энциклопедия
Уравнения Максвелла — Классическая электродинамика … Википедия
ПРАВИЛА СУММ — теоретич. соотношения, фиксирующие значение нек рой суммы (интеграла) матричных элементов, характеризующих переходы между состояниями рассматриваемой системы. Широкое применение П. с. в физике связано с тем, что во мн. случаях из теоретич.… … Физическая энциклопедия
Заряд (физика) — Эта статья о понятии заряда в самом общем физическом смысле. О заряде, связанном с электрическими явлениями см. Электрический заряд; о других значениях см. Заряд (значения). В физике понятие заряд используется для… … Википедия
Чайковский (город) — Город Чайковский Герб … Википедия
Родина (кинокамера) — У этого термина существуют и другие значения, см. Родина (значения). «Родина» 3КСХ Производитель «Москинап» Год выпуска 1953 1975 … Википедия
НЕЛИНЕЙНАЯ ОПТИКА — раздел оптики, охватывающий исследования распространения мощных световых пучков в тв. телах, жидкостях и газах и их вз ствия с в вом. Сильное световое поле изменяет оптич. хар ки среды (показатель преломления, коэфф. поглощения), к рые становятся … Физическая энциклопедия
Силовые вилки и розетки для переменного тока — Эта статья о конструкции, технических особенностях и истории развития штепсельных разъёмов. О стандартах на штепсельные разъёмы, принятых в разных странах см. Список стандартов штепсельных разъёмов … Википедия
Ту-22М — Не следует путать с Ту 22. Ту 22М … Википедия
Задача 3. 4.3.1. При расчетах цепей переменного синусоидального тока используются те же законы и методы, что и при расчете цепей постоянного тока



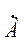
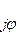
где А – модуль величины,
а и b – ее действительная и мнимая части.
А = 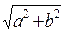
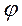
для перехода от показательной формы записи к алгебраической нужно использовать выражения
а = А cos 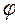
b = A sin 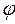
4.3.2.При составлении расчетной схемы необходимо:
а) заменить полные сопротивления составляющими их элементами: активными сопротивлениями, индуктивностями и емкостями;
б) источники тока источниками ЭДС.
Ветви с источниками тока, равными нулю, на схему не наносятся.
4.3.3. Для определения линейной частоты f следует использовать связывающее ее с угловой частотой 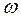
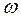
4.3.4. Расчет токов в ветвях следует вести в изложенной ниже последовательности
а) Вычислить сопротивления реактивных элементов
ХL = 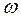
ХC = 1/ 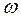
б) Записать в комплексной форме заданные величины, используя приведенные в п. 4.3.1 формулы.
— ЭДС дана в виде Е = 100 В; 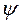
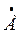
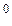
а перевод ее в алгебраическую форму выполняется по (4) и (5);
— сопротивление ветви состоит из резистора R, индуктивного ХL и емкостного ХС сопротивлений
R = 3 Ом; ХL = 9 Ом; ХС = 5 Ом. Тогда удобней первоначальную запись комплексного сопротивления выполнить в алгебраической форме
Z = R + j (ХL – ХС) = 3 + j (9 – 5) = 3 + j 4
c последующим ее переводом в показательную форму по (4.3.1) – (4.3.3).
Результаты расчетов занести в таблицу 6.
в алгебраической и показательной форме.
| Величина, параметр | Алгебраическая форма | Показательная форма |
в) Составить контурные уравнения для своей расчетной схемы замещения, используя выражение ЭДС и сопротивлений комплексными числами. Для упрощения операций умножения и деления при составлении уравнений предпочтительней использовать показательную форму комплексов.
г) Решить полученную систему уравнений и, найдя контурные токи, определить токи в ветвях, напряжения на каждом комплексном сопротивлении и их элементах. Результаты расчетов занести в таблицу 7. Количество строк в таблице зависит от числа найденных величин.
| Искомая величина | Алгебраическая форма | Показательная форма | Действующее значение |
Правильность расчетов может быть проверена по уравнениям, составленным по первому закону Кирхгофа.
4.3.5. Найти комплекс мощности S источника питания как произведение комплекса ЭДС источника на сопряженный комплекс тока 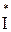
При использовании показательной формы необходимо в сопряженном комплексе изменить знак показателя.
Заменой комплекса тока на его сопряженный комплекс учитывается угол сдвига фаз между ЭДС и током для источников питания (напряжением и током для приемников).
Полная мощность равна модулю комплекса мощности, или
S = Е I,(4.3.10)
а действительная и мнимая части комплекса мощности соответствуют активной и реактивной мощности, или
Р = S cos 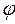
Q = S sin 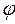
где 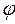
Суммарную мощность всех действующих в цепи источников питания проще найти, записав комплексы мощностей каждого источника в алгебраической форме.
Результаты определения мощностей показать в таблице, форму которой составить самостоятельно.
4.3.6. Для составления баланса активных мощностей следует определить активную мощность, потребляемую активными сопротивлениями (резисторами) n-й ветви цепи
где In – действующее значение тока ветви, А;
Rn – активное сопротивление ветви, Ом.
Потребляемая цепью активная мощность должна быть равна активной мощности, отдаваемой всеми источниками питания (см. п. 4.3.5).
4.3.7. Уравнения мгновенных значений заданных ЭДС имеют вид
е = Еm sin ( 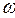
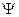
где 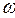
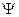
4.3.8. Построение векторной диаграммы.
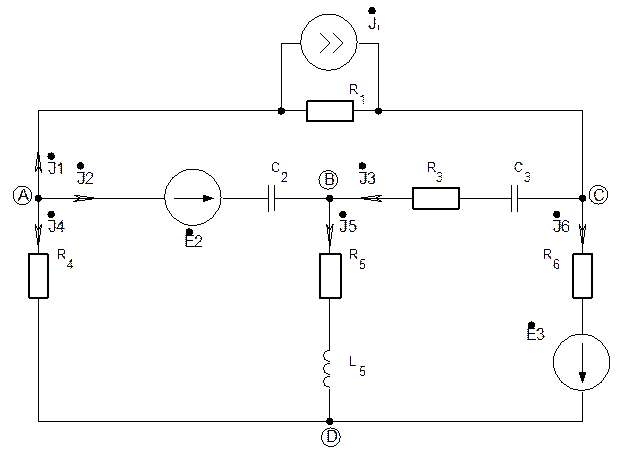
Рис. 12. Схема однофазной цепи
| Искомая величина | Алгебраическая форма | Показательная форма | Действующее значение | |
| Токи ветвей, А | 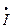 1 1 | I’1 + jI»1 | I1 e 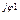 | I1 |
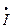 2 2 | I’2 + jI»2 | I2 e 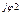 | I2 | |
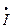 3 3 | I’3 + jI»3 | I3 e 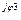 | I3 | |
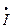 4 4 | I’4 + jI»4 | I4 e 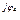 | I4 | |
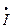 5 5 | I’5 + jI»5 | I5 e 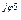 | I5 | |
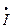 6 6 | I’6 + jI»6 | I6 e 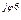 | I6 |
Продолжение таблицы 7а
| Напряжения на сопротивлениях, В |  1 = 1 =  R1 R1 | U’1 + j U»1 | U1 e 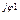 | U1 |
 2 = 2 =  C2 C2 | U’2+ jU»2 | U2 e 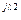 | U2 | |
 3 3 | U’3 + jU»3 | U3 e 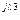 | U3 | |
 R3 R3 | U’R3 + jU»R3 | UR3 e 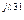 | UR3 | |
 C3 C3 | U’C3 + jU»C3 | UC3 e 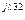 | UC3 | |
 4 = 4 =  R4 R4 | U’4 + jU»4 | U4 e 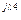 | U4 | |
 5 5 | U’5 + jU»5 | U5 e 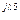 | U5 | |
 R5 R5 | U’R5 + jU»R5 | UR5 e 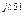 | UR5 | |
 5 5 | U’L5 + jU»L5 | UL5 e 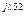 | UL5 | |
 6 = 6 =  R6 R6 | U’6 + jU»6 | U6 e 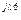 | U6 |
На рис. 13 дана векторная диаграмма токов и напряжений в цепи, при построении которой соблюдалась следующая последовательность:
1. Строятся оси комплексной плоскости: действительных величин (+1) – горизонтально, мнимых величин (j) – вертикально.
2. Исходя из значений модулей токов и напряжений и размеров поля листа, отведенного для построения диаграммы, выбираются масштабы тока mI и напряжения mU. Например, при использовании формата А4 (размеры 210х297 мм) при наибольших модулях тока 40 А и напряжения U = 500 В приняты масштабы: mI = 5 А/см, mU = 50 В/см.
3. С учетом принятых масштабов mI и mU определяется длина каждого вектора, если диаграмма строится с использованием показательной формы его записи; при использовании алгебраической формы находятся длины проекций векторов на оси действительных и мнимых величин, т.е. длины действительной и мнимой частей комплекса.
Например, для записанных в комплексной форме тока, I = 40 е 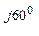
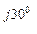
— длина вектора тока /I / = 40 А/ 5 А/см = 8 см; длина его действительной части I = 20 А / 5 А/см = 4 см, длина его мнимой части I = 34,6 А / 5 А/см = 6,9 см;
— длина вектора напряжения / U / = 500 В / 50 В/см = 10 см; длина его действи-
тельной части U = 433 В / 50 В/см = 8,66 см; длина его мнимой части U =
= 250 В / 50 В/см = 5 см.
Результаты определения длин векторов, их действительных и мнимых частей нужно отразить в таблице 7б.
| Величина | Масштаб, 1/см | Длина вектора, см | Длина действительной части, см | Длина мнимой части, см |
| Токи ветвей | 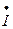 1 1 | mI= 5 А/см | ||
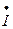 2 2 | ||||
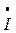 3 3 | ||||
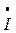 4 4 | ||||
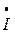 5 5 | ||||
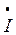 6 6 | ||||
| ЭДС и напряжения | 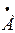 1 1 | mU=50 В/см | ||
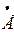 2 2 | ||||
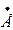 6 6 | ||||
 1= 1=  R1 R1 | ||||
 R1 R1 | ||||
 2 = 2 =  C2 C2 | ||||
 3 3 | ||||
 R3 R3 |
Продолжение таблицы 7б
| ЭДС и напряжения |  C3 C3 | mU=50 В/см |
 4 = 4 =  R4 R4 | ||
 5 5 | ||
 R5 R5 | ||
 L5 L5 | ||
 6 = 6 =  R6 R6 |
4. На комплексной плоскости строятся вектора всех ЭДС, напряжений и токов. Для их построения можно использовать обе формы записи комплексов ЭДС, напряжений и токов.
Например, вектор тока 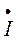
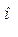
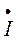
На векторной диаграмме (рис. 13) использованы оба способа построения векторов: векторы токов построены по показательной форме записи, а векторы ЭДС и напряжений по алгебраической.
5. Правильность расчета цепи и построения векторной диаграммы проверяется по взаимному расположению векторов, а также их сложением. Так, например,
для используемой в качестве примера схемы (рис. 12):
— векторы токов 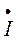



— вектор напряжения 

— сумма токов узла В 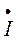
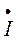
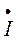
— по второму закону Кирхгофа для контура 111 при сложении векторов напряжений 


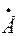
Таким образом может быть выполнена проверка для всех ветвей, узлов и контуров.
Рис. 13. Векторная диаграмма токов и напряжений для схемы на рис. 12.