Что такое составить выражение в математике 4 класс
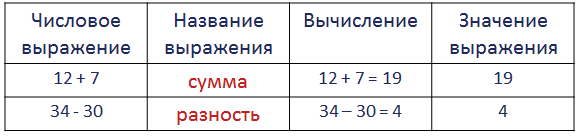
Числовые и буквенные выражения
Числовые выражения
В этом разделе мы узнаем, что называют числовым выражением и значением выражения, научимся читать выражения.
Значение выражения — это результат выполненных действий.
Чтение числовых выражений
Решение числовых выражений
45 – (30 + 2) = …
Сначала выполняем действие, записанное в скобках. К 30 прибавляем 2.
30 + 2 = 32
Теперь нужно из 45 вычесть 38.
45 – 32 = 13
45 – (30 + 2) = 13
Сравнение значений числовых выражений
Сравнить числовое выражение – найти значение каждого из выражений и их сравнить.
Для этого найдем значения каждого из них:
Буквенные выражения
Буквенным называется математическое выражение, в котором используются цифры, знаки действий и буквы. Например, (47 + d) – 11.
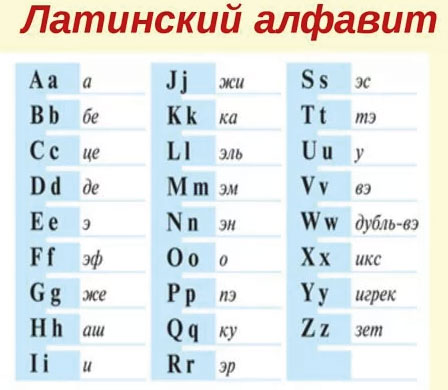
Для записи буквенных выражений необходимо знать некоторые буквы латинского алфавита. Мы приводим его полностью, чтобы ты знал, с какими буквами можешь встретиться при составлении, решении или чтении буквенных выражений.
Чаще всего используются буквы:
a, b, c, d, x, y, k, m, n
Алгоритм решения буквенного выражения
1. Прочитать буквенное выражение
2. Записать буквенное выражение
3. Подставить значение неизвестного в выражении
4. Вычислить результат
Читаем выражение: Из 28 вычесть с или Найти разность числа 28 и с
Подставим вместо неизвестного «с» число 4.
У нас получается выражение: 28 – 4
Переменные
Буквы, которые содержатся в буквенных выражениях называются переменными. Например, в выражении с + x + 2 переменными являются буквы c и x. Если вместо этих переменных подставить любые числа, то буквенное выражение с + x + 2 обратится в числовое выражение, значение которого можно будет найти.
Числа, которые подставляют вместо переменных называют значениями переменных. Например, изменим значения переменных c и x. Для изменения значений используется знак равенства
Мы изменили значения переменных c и x. Переменной c присвоили значение 2, переменной x присвоили значение 3, тогда выражение с + х + 2 будет выглядеть так:
Теперь мы можем найти значение этого выражения:
с + х + 2 = 2 + 3 + 2 = 5 + 2 = 7
Поделись с друзьями в социальных сетях:
Числовые и буквенные выражения. Порядок действий.
теория по математике 📈 алгебраические выражения
Числовое выражение – это выражение, состоящее из чисел и знаков действий, а также скобок.
Пример №1. В каждом из этих выражений содержатся числа, между которыми есть знаки действий, а также бывают скобки. Это и есть числовые выражения.
Если выполнить по порядку все действия, которые есть в числовом выражении, то получится определенное число, которое называют значением числового выражения. Порядок действий в числовых выражениях определяется правилами.
Действия сложение и вычитание принято называть действиями первой ступени, а умножение и деление – действиями второй ступени. Возведение в степень – это действие третьей ступени.
Порядок действий в выражении, не содержащем скобки
890 – 567 + 2340 – 124
в данном выражении действия одной ступени (сложение и вычитание), поэтому выполняем их по порядку слева направо:
в этом выражении также действия одной ступени (умножение и деление), поэтому выполняем их по порядку слева направо:
здесь присутствуют действия всех ступеней. Поэтому начинаем выполнять их с наивысшей ступени – возведения в степень. Затем слева направо выполняем деление и умножение, а затем слева направо – сложение и вычитание:
Порядок действий в выражении, содержащем скобки
Если числовое выражение содержит скобки, то выполняют сначала действия в скобках, следуя правилу, а затем – действия за скобками.
(3245 + 67,92:2)×3 + (126×2 – 321:3) – 125
здесь числовое выражение содержит скобки, поэтому действия выполняем в скобках слева (деление, затем сложение), затем в скобках справа (умножение, деление, вычитание):
Теперь выполняем действия за скобками слева направо (умножение, сложение, вычитание):
Буквенные выражения. Числовое значение буквенного выражения.
Выражения, содержащие не только числа и знаки действий, но и буквы, называют буквенными. Буквы также можно называть «переменная». Обращаем внимание на то, что знак «умножить» между числом и буквой не пишется.
Пример №6. Примеры буквенных выражений:
Числовое значение буквенного выражения – это значение числового выражения, полученного при подстановке конкретных значений переменной в данное выражение.
Пример №7. Найдем значение выражения с + х при с=23, х=0,17. Для этого подставим вместо с и х их данные числовые значения и получим числовое выражение 23 + 0,17. Теперь вычислим результат и получим 23,17. Таким образом, числовое значение буквенного выражения с + х равно 23,17.
Пример №8. Н айдем значение выражения 11х +(с — d) при х=10, c=178, d=121. Для этого подставляем вместо каждой переменной соответствующие числовые значения и получим числовое выражение 11×10 + (178 – 121). Выполнив действия, получим ответ 167. Это и есть числовое значение буквенного выражения.
Заметим, что и числовые и буквенные выражения можно называть еще как алгебраические выражения.
В данном случае необходимо сначала упростить выражение, для этого раскроем скобки:
(x + 5) 2 — x (x — 10) = x 2 + 2 • 5 • x + 25 — x 2 + 10x
Затем приведем подобные слагаемые:
x 2 + 2 • 5 • x + 25 — x 2 + 10x = 20 x + 25
Далее подставим x из условия:
20 x + 25 = 20 • (-1/20) + 25 = — 1 + 25 = 24
pазбирался: Даниил Романович | обсудить разбор | оценить
На координатной прямо отмечены числа a и b:
Какое из приведенных утверждений для этих чисел неверно:
Для удобства решения необходимо оценить данные нам числа. Из координатной прямой видно, что a > 0, так как расположено справа от ноля, а b 0
Значит, утверждение неверно.
pазбирался: Даниил Романович | обсудить разбор | оценить
Урок математики в 4 классе Тема: Выражение и его значение. Порядок выполнения действий.
Урок математики в 4 классе Тема: Выражение и его значение. Порядок выполнения действий.
Цели: актуализировать знания об основных арифметических действиях (сложение, вычитание, умножение, деление), о связи между компонентами и результатами этих действий; повторить правила порядка выполнения действий в выражениях; совершен-ствовать вычислительные навыки, умение решать задачи.
Планируемые результаты: учащиеся научатся читать и запи¬сывать трехзначные числа; находить значения выражений в не¬сколько действий; находить несколько способов решения задач; анализировать свои действия в соответствии с поставленной учеб¬ной задачей; оценивать результаты своей работы и при необходи¬мости исправлять ошибки с помощью учителя.
I. Организационный момент
II. Актуализация знаний
1. Логические задачи
• Полный бидон с молоком весит 34 кг, бидон, заполненный наполовину, весит 18 кг. Сколько весит пустой бидон?
1) 34 — 18 = 16 (кг) — весит половина молока;
Ответ: пустой бидон весит 2 кг.
• Боря начертил два треугольника. Для обозначения вершин треугольников ему понадобилось только пять букв. Как такое может быть? (Боря начертил треугольники, которые имели общую вершину.)
2. Индивидуальная работа у доски
— Запиши числа цифрами. Пятьсот пять, триста восемьдесят, шестьсот двадцать семь, девятьсот семьдесят, триста, девятьсот семь.
— Уменьши каждое число на 7, запиши ниже.
562-60 760-600 950-1 769 + 10
462 + 48 600-35 788-89 652-37
3. Выполнение задания в рабочей тетради
№3(с.3). (Индивидуальная работа.)
— Сосчитайте от 397 до 402, от 788 до 800, от 505 до 494, от 1000 до 989.
— Прочитайте числа. 342, 402, 360, 900, 540.
— Сколько сотен, десятков, единиц в каждом числе?
— Сколько всего десятков в каждом числе? (342 — 34 десятков, 402 — 40 десятков, 360 — 36 десятков, 900 — 90 десятков 540- 54 десятка.)
— Сколько всего сотен в каждом числе? (342 — 3 сотни, 402- 4 сотни, 360 — 3 сотни, 900 — 9 сотен, 540 — 5 сотен.)
— Прочитайте числа в порядке возрастания. (342, 360, 40 540, 900.)
— Прочитайте числа в порядке убывания. (900,540, 402,360,341)
— Какое число может быть лишним? Почему? (342 — нет нулей, 402 — в сумме цифры не составляют 9, 900— есть только один разряд — сотни.)
(Проверка индивидуальной работы у доски.)
III. Самоопределение к деятельности
— Какие действия вы выполняли при решении примеров (Сложение и вычитание.)
— Какими знаками они обозначаются? («+» и «-».)
— Назовите знаки действий, которые использованы в следующих выражениях.
(Три ученика выходят к доске и решают примеры.)
— Сравните примеры. Чем они похожи? (Одинаковые числа и знаки.)
— Чем отличаются? (По-разному расставлены скобки, значит, порядок действий и ответы тоже будут разными.)
— Сформулируйте задачи урока. (Повторить то, что нам из¬вестно об арифметических действиях сложения и вычитания, вспомнить правила о порядке выполнения действий в выраже¬ниях, научиться находить значения выражений, содержащих несколько действий.)
IV. Работа по теме урока Работа по учебнику
— Прочитайте текст рядом с красной чертой на с. 6.
— Что такое числовое выражение? (Числа, соединенные знаками арифметических действий.)
— Какие правила порядка выполнения действий вы знаете? (Первое действие выполняют в скобках, затем умножение или деление, а потом сложение и вычитание по порядку.)
— Как выполняются действия, если скобок несколько пар? (По порядку в каждых скобках, а затем по правилам.)
№ 11 (с. 6). (Фронтальная работа.)
№13 (с. 6). — Прочитайте задачу.
— Кто понял, как ее решать? Запишите решение задачи вы¬ражением.
(Те, кто испытывает затруднения, берут карточку-помощницу со схематическим рисунком.) (Проверка, самооценка.)
Решение: 50 + 5 • 8 = 90 (руб.). Ответ: у Нины было 90 руб.
№14 (с. 6). — Прочитайте задачу.
— Что нужно знать, чтобы сказать, сколько мест в 7 вагонах? (Сколько мест в одном вагоне.)
— Как узнать, сколько мест в одном вагоне? (120:2.)
2. Порядок действий в числовых выражениях. Сложение и вычитание
— Запишите решение задачи выражением.
(Один ученик работает на откидной доске. Проверка, само¬оценка.)
№9 18 (с. 7). (Устное выполнение.) — Прочитайте задачу.
— Объясните, что обозначают выражения.
(Для учащихся, которые затрудняются объяснить, что обозна¬чают выражения, необходимо составить таблицу.)
Масса одного пакета Количество пакетов Общая масса семян
1) 250 : 5 — узнаем, сколько упаковали пакетов с семенами астр;
— Запишите решение этой задачи. (250: 5 — 240: 8 — 20 (п.).)
Шеей крутим осторожно –
Голова кружиться может.
Влево смотрим — раз, два, три.
Так. И вправо посмотри. (Вращения головой вправо и влево.)
Вверх потянемся, пройдемся (Потягивания —руки вверх. Шаги на месте.)
И на место вновь вернемся. (Сесть за парту.)
VI. Закрепление изученного материала
1. Работа по учебнику
№15 (с. 7). — Рассмотрите таблицу.
— Что неизвестно в каждом столбике? Как мы находим не¬известное? (В первом столбике неизвестна сумма. Чтобы найти сумму, надо к первому слагаемому 170 прибавить вто¬рое слагаемое 230. Сумма 400. Во втором столбике неизвестно первое слагаемое. Чтобы найти первое слагаемое, надо из суммы 330 вычесть второе слагаемое 40. Первое слагаемое 290.)
(Аналогичная работа проводится с каждым столбиком каждой таблицы.)
— Посмотрите на записи на полях и сформулируйте правила.
(1. Если к числу прибавить ноль, то получится это же число.
2. Если из числа вычесть ноль, то получится это же число.
3. Если из числа вычесть такое же число, то получится ноль.)
— Какие еще свойства сложения вы знаете? (От перестановки мест слагаемых сумма не изменяется.)
— Запишите его, используя буквы, (а + с = с + а.)
№16 (с. 7). (Устная фронтальная работа.)
— Что неизвестно в каждом уравнении?
— Как найти неизвестный компонент?
— Чему равен х в каждом уравнении?
— Замените одно из чисел в каждом уравнении так, чтобы х не был равен нулю, а в последнем уравнении так, чтобы значение разности не было равно нулю.
2. Выполнение заданий в рабочей тетради
№4(с.3). (Устное выполнение.)
№5(с.3). (Самостоятельное выполнение. Проверка. Самооценка.)
(Самостоятельное выполнение задания «Проверь себя» (учеб¬ник, с. 7). Самопроверка по образцу.) Ответ: 80.
— Оцените свою работу на уроке.
VIII. Подведение итогов урока
— Что мы повторили сегодня на уроке?
— Кто может сказать, что он хорошо решает задачи?
— Какие задания вам показались самыми трудными?
Математика. 4 класс
Конспект урока
Математика, 4 класс
Урок №2. Числовые выражения. Порядок выполнения действий.
Сложение нескольких слагаемых
Перечень вопросов, рассматриваемых в теме:
— что такое «числовые выражения»?
— что значит «Найти значение выражения»?
— как устанавливается порядок действий в выражениях со скобками и без?
Сложение чисел – математическая операция по объединению частей в одно целое. На письме обычно обозначается с помощью знака «плюс»
Вычитание чисел – математическая операция по вычитанию из целого части. На письме обычно обозначается с помощью знака «минус».
Умножение чисел – математическая операция, в результате которой находят сумму одинаковых слагаемых.
Деление чисел – математическая операция обратная умножению.
Числовое выражение – числа, соединенные знаками арифметических действий для выполнения вычисления.
Значение выражения –число, которое получается после выполнения всех действий.
Скобки в выражениях – знаки «( )», которые позволяют разграничить и определить порядок действий.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 4 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 7-9
2. Математика: 4 класс: учебник в 2 ч. Ч.1/ В. Н. Рудницкая, Т. В. Юдачева. – М. Вентана-Граф, 2016. – с. 13-15
3. Математика: 4 класс/ Т. Е. Демидова, С. А. Козлова, А. П. Тонких О. – М.; БАЛАСС, 2008. – с. 11-12
Теоретический материал для самостоятельного изучения
Существуют следующие правила порядка действий в числовых выражениях.
Правило 1. Если числовое выражение содержит только сложение и вычитание, или только умножение и деление, то действия выполняются по порядку.
Правило 2.Если числовое выражение содержит не только сложение и вычитание, но и умножение и деление, то сначала выполняются по порядку (слева направо) действия умножение и деление, а потом – сложение и вычитание (слева направо).
Правило 3.Если числовое выражение содержит одну пару или несколько пар скобок, то сначала находят значение выражения в скобках, а затем выполняют действия по правилам 1 и 2.
Порядок выполнения действий
В данном разделе мы познакомимся с порядком действий, с выражениями со скобками и без них.
1) Если тебе нужно выполнить только сложение и вычитание или только умножение и деление, то все действия выполняют по порядку слева направо.
Например,
В числовом выражении 3 арифметических действия: сложение, вычитание и вычитание.
Определим порядок действий и запишем их над арифметическими знаками: так как нет ни умножения ни деления, действия выполняют по порядку слева направо:
Полностью пример записываем так:
Например,
В числовом выражении 3 арифметических действия: деление, умножение и деление.
Определим порядок действий и запишем их над арифметическими знаками: так как нет ни сложения ни вычитания, действия выполняют по порядку слева направо:
Полностью пример записываем так:
15 : 5 • 4 : 6 = 3 • 4 : 6 = 12 : 6 = 2
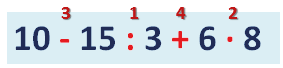
2) Если тебе нужно выполнить несколько арифметических действий (сложение, вычитание, умножение и деление), то сначала выполняют умножение и деление по порядку слева направо, а затем сложение и вычитание по порядку слева направо.
Например,
В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим деление, потом умножение, затем вычитание и сложение.
Полностью пример записываем так:
3) Если в выражении есть скобки, то сначала выполняют действия в скобках, но обязательно учитывать первое и второе правила.
Например,
В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим вычитание в скобках, затем деление, потом умножение и сложение.
Полностью пример записываем так:
Например,
В числовом выражении 4 арифметических действия: сложение, деление, сложение и деление.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим действия в скобках (деление, затем сложение), затем деление, потом сложение.
Полностью пример записываем так:
42 + 18 : (6 + 12 : 4) = 42 + 18 : (6 + 3) = 42 + 18 : 9 = 42 + 2 = 44
Вывод:
Поделись с друзьями в социальных сетях: