Что такое составное логическое высказывание
Составные высказывания и логические выражения
2.1. Составные высказывания
Из элементарных высказываний можно строить более сложные (составные) высказывания, используя связки И, ИЛИ, НЕ.
Примеры. Забор красный И забор деревянный.
Коля старше, чем Петя ИЛИ Коля старше, чем Федя
Смысл этих высказываний понятен.
Высказывание с НЕ содержит одно элементарное высказывание (в русском языке НЕ часто ставится в середину этого высказывания). Составное высказывание с НЕ истинно, если исходное элементарное высказывание ложно и, наоборот, если исходное высказывание истинно, то составное высказывание с НЕ ложно.
Составные высказывания можно строить не только из элементарных высказываний, но и из других составных высказываний. В этом построение составных высказываний похоже на построение алгебраических выражений. Например, понятно, что означает такое высказывание (хотя оно написано не на русском языке, а с использованием скобок : )
(Коля старше, чем Петя ИЛИ Коля старше, чем Федя) И (Коля НЕ старше, чем Ваня)
Здесь 3 элементарных высказывания.
2.2. Логические значения. Логические операции.
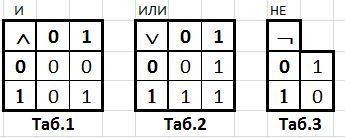
Так как логических значений всего два, то эти операции можно описать таблицами.
У операций И, ИЛИ, НЕ есть «научные» названия (даже несколько для каждой операции 🙂 и специальные обозначения (в примерах A, B обозначают какие-то конкретные логические значения):
НЕ: отрицание, инверсия. Обозначение: ¬ (например, ¬А);
И: конъюнкция, логическое умножение.
Обозначается /\ (например, А /\ В) либо & (например, А & В);
ИЛИ: дизъюнкция, логическое сложение.
Обозначается \/ (например, А \/ В).
В математике используются и другие логические операции.
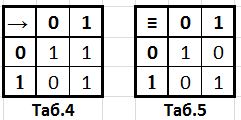
Каждая логическая операция может быть задана своей таблицей. Вот еще два примера логических операций:
1) следование (импликация); обозначается → (например, А → В); см. таб. 4. Выражение А → В истинно если A ложно ИЛИ B истинно. То есть, А → В означает то же самое, что и (¬А) \/ В.
2) тождество (эквивалетность); обозначается ≡ (например, A ≡ B); см. таб 5. Выражение A ≡ B истинно тогда и только тогда, когда значения A и B совпадают (либо они оба истинны, либо они оба ложны).
Логические операции играют для логических значений ту же роль, что и арифметические операции для чисел. Аналогично построению алгебраических выражений, с помощью логических операций можно строить логические выражения. Как и алгебраические выражения, логические выражения могут включать константы (логические значений 1 и 0) и переменные. Если в логическом значении есть переменные, оно задает функцию (логическую функцию; синоним: булеву функцию). Значение такой функции при заданном наборе значений аргументов вычисляется подстановкой этих значений в выражение вместо переменных.
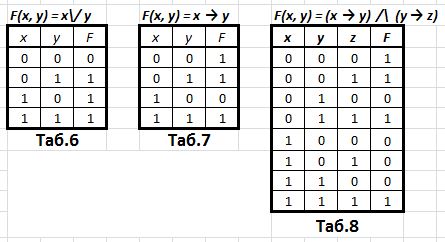
Для каждого логического выражения можно составить таблицу истинности, которая описывает, какое значение принимает соответствующая логическая функция (синоним: принимает выражение) при каждом допустимом наборе значений переменных. Вот таблицы истинности для выражений x \/ y (таблица 6), x → y (таблица 7) и (x → y) /\ (y → z) (таблица 8).
2.4. Эквивалентные выражения.
Два логических выражения, содержащих переменные, называются равносильными (эквивалентными), если значения этих выражений совпадают при любых значениях переменных. Так, выражения А → В и (¬А) \/ В равносильны, а А/\В и А \/ В – нет (значения выражений разные, например, при А = 1, В = 0).
Эквивалентные выражения имеют одинаковые таблицы истинности, а у неээквивалентных выражений таблицы истинности различны.
2.5. Приоритеты логических операций.
При записи логических выражений, как и при записи алгебраических выражений, иногда можно не писать скобки При этом соблюдаются следующие договоренности о старшинстве (приоритете) логических операций, первыми указаны операции, которые выполняются в первую очередь:
конъюнкция (логическое умножение),
дизъюнкция (логическое сложение),
Таким образом, ¬А \/ В \/ С \/ D означает то же, что и ((¬А) \/ В)\/ (С \/ D).
Возможна запись А \/ В \/ С вместо (А \/ В) \/ С. То же относится и к конъюнкции: возможна запись А /\ В /\ С вместо (А /\ В) /\ С.
4 комментария
2.3. Логические выражения. Таблицы истинности.
Значение такой функции при заданном наборе значений аргументов вычисляется подстановкой этих значений в МЫРАЖЕНИЕ вместо переменных
Что такое составное логическое высказывание

2. Построение таблиц истинности и логических функций.
3. Законы логики и преобразование логических выражений.
Лабораторная работа № 3. Основы математической логики.

Исследования в алгебре логики тесно связаны с изучением высказываний (хотя высказывание — предмет изучения формальной логики). Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности (Аристотель).
Простым высказыванием называют повествовательное предложение, относительно которого имеет смысл говорить, истинно оно или ложно.
Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным.
Высказывания 1 и 3 являются истинными. Высказывание 2 – ложным , потому что число 27 составное 27=3*3*3.
Итак, отличительным признаком высказывания является свойство быть истинным или ложным, последние четыре предложения этим свойством не обладают.
С помощью высказываний устанавливаются свойства, взаимосвязи между объектами. Высказывание истинно, если оно адекватно отображает эту связь, в противном случае оно ложно.
Однако определение истинности высказывания далеко не простой вопрос. Например, высказывание «Число 1 +22 = 4294 967297 — простое», принадлежащее Ферма (1601-1665), долгое время считалось истинным, пока в 1732 году Эйлер (1707-1783) не доказал, что оно ложно. В целом, обоснование истинности или ложности простых высказываний решается вне алгебры логики. Например, истинность или ложность высказывания «Сумма углов треугольника равна 180°» устанавливается геометрией, причем в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным.
В булевой алгебре простым высказываниям ставятся в соответствие логические переменные, значение которых равно 1, если высказывание истинно, и 0, если высказывание ложно. Обозначаются логические переменные, большими буквами латинского алфавита.
Существуют разные варианты обозначения истинности и ложности логических переменных:
Сложные (составные) высказывания представляют собой набор простых высказываний (по крайней мере двух) связанных логическими операциями.
С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой (логическим выражением).
Связки «НЕ», «И», «ИЛИ» заменяются логическими операциями инверсия, конъюнкция, дизъюнкция. Это основные логические операции, при помощи которых можно записать любое логическое выражение.
Введем перечисленные логические операции.
В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.