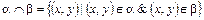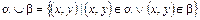Что такое составные отношения

Операции над бинарными отношениями

Так как отношения на X задаются подмножествами, aÍX´X, для них определены те же операции, что и над множествами.

Возьмем два отношения α и b. Каждому из них соответствует некоторое множество пар (подмножества aÍX´X и bÍ X´X).

Определение 3.14. Пересечением отношений αÇb называется отношение, определяемое пересечением соответствующих подмножеств.

Ясно, что x(αÇb)y выполнено тогда и только тогда, когда одновременно выполнены соотношения xαy и xby.

Определение 3.15. Объединением отношений αÈb называется отношение, определяемое объединением соответствующих множеств.

Соотношение x(αÈb)y выполнено тогда и только тогда, когда выполнено хотя бы одно их соотношений xαy или xby.

Пример. Если α – отношение «больше» на множестве чисел, а b – отношение «равно», то αÈb – это отношение ≥.

Определение 3.16. Обратным отношением называется отношение, определяемое условием: .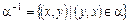

Определение 3.17. Разностью будем называть отношение, удовлетворяющее условию .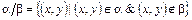

Определение 3.18. Разностью будем называть отношение, удовлетворяющее условию 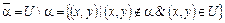, где U

Определение 3.19. Составное отношение (композицией) называется отношение, определяемое следующим образом: .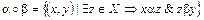

Пример. Пусть α – отношение «быть братом», а b – отношение «быть родителем». Тогда произведение αb есть отношение «быть братом одного из родителей», т.е. «быть дядей».

Лемма 3.4. Чтобы составное отношениеαb симметричных отношений α и b было симметрично, необходимо и достаточно, чтобы отношения α и b коммутировали.

Антисимметричность может не сохраняться при объединении и композиции.

Из лемм 3.2, 3.3, 3.4, 3.5 вытекают следующие две теоремы.

Теорема 3.6. Если α и b – строгие порядки (нестрогие порядки), то пересечение αÇb также является строгим порядком (нестрогим порядком).

Замечание. Пересечение строгого и нестрогого порядка есть строгий порядок.

Теорема 3.8. Если α и b – строгие порядки, то объединение αÈb является строгим порядком в том и только том случае, когда .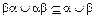

Теорема 3.9. Для того чтобы объединение αÈb нестрогих порядков α и b было нестрогим порядком, необходимо и достаточно выполнение условий , .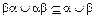

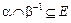
Композицией порядков αb также не обязано быть порядком. Это видно из того хотя бы, что для линейного нестрогого порядка α композиция 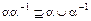есть полное отношение. Достаточным условием является, например, такое.

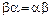
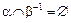
Теорема 3.10. Если α и b – строгие порядки и выполнены соотношения: , , то αb – строгий порядок.

Источник

Учитель информатики

Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.

§ 3. Отношения объектов и их множеств

Информатика. 6 класса. Босова Л.Л. Оглавление

Ключевые слова:

Разнообразие отношений.

Человек может рассказать не только о признаках объекта, но и об отношениях, в которых этот объект находится с другими объектами. Например:

В каждом из приведённых предложений выделено имя отношения, которое обозначает характер связи между двумя объектами.

Отношение — это взаимная связь, в которой находятся какие-либо объекты.

Одним и тем же отношением могут быть попарно связаны несколько объектов. Соответствующее словесное описание может оказаться очень длинным, и тогда в нём трудно разобраться.

Пусть про населённые пункты А, Б, В, Г, Д и Е известно, что некоторые из них соединены железной дорогой: населённый пункт А соединён железной дорогой с населёнными пунктами В, Г и Е, населённый пункт Е — с населёнными пунктами А, В, Г и Д.

Для большей наглядности имеющиеся связи («соединён железной дорогой») можно изобразить линиями на схеме отношений. Объекты на схеме отношений могут быть изображены кругами, овалами, точками, прямоугольниками и т. д. (рис. 4).

Имена некоторых отношений изменяются, когда меняются местами имена объектов, например: «выше» — «ниже», «приходится отцом» — «приходится сыном». В этом случае направление отношения на схеме отношений обозначают стрелкой.

Так, на рис. 4 каждая стрелка направлена от отца к его сыну и поэтому отражает отношение «приходится отцом», а не «приходится сыном». Например: «Андрей приходится отцом Ивану».

Стрелки можно не использовать, если удаётся сформулировать и соблюсти правило взаимного расположения объектов на схеме. Например, если на рис. 5 имена детей всегда располагать ниже имени их отца, то можно обойтись без стрелок.

Такие отношения, как «приходится сыном», «соединён железной дорогой», «покупает», «лечит» и т. д., могут связывать только объекты некоторых видов. В отношениях «является элементом множества», «входит в состав» и «является разновидностью» могут находиться любые объекты.

Отношения могут существовать не только между двумя объектами, но и между объектом и множеством объектов, например:

В каждом из этих предложений описано отношение «является элементом множества».

Отношения между множествами

Отношения могут связывать два множества объектов, например:

Графически множества удобно представлять с помощью кругов, которые называют кругами Эйлера.

Если множества А и В имеют общие элементы, т. е. элементы, принадлежащие одновременно А и В, то говорят, что эти множества пересекаются (рис. 6).

Пример. Пусть А — множество электронных писем, В — множество писем на русском языке. В пересечение этих множеств попадают все электронные письма на русском языке.

Если множества не имеют общих элементов, то говорят, что они не пересекаются (рис. 7).

Пример. Пусть А — множество компьютерных устройств ввода информации, В — множество устройств вывода информации. Эти множества не имеют общих элементов.

Если каждый элемент множества В является элементом множества А, то говорят, что В — подмножество А (рис. 8).

Пример. Пусть А — множество учеников, В — множество шестиклассников. Множество шестиклассников является подмножеством множества учеников.

Если каждый элемент множества В является элементом множества А и, наоборот, каждый элемент множества А является элементом множества В, то говорят, что множества А и В равны (рис. 9).

Пример. Пусть А — множество равносторонних прямоугольников, В — множество квадратов. Эти множества равны.

Отношение «входит в состав»

В зависимости от ситуации объект может либо рассматриваться как единое целое, либо «распадаться» на более мелкие объекты. Например, компьютер рассматривается как единое целое, если нужно подсчитать количество компьютеров в школе. Чтобы получить представление о возможностях компьютера, необходимо рассмотреть характеристики таких его устройств, как процессор, память, жёсткий диск и т. д.

Объект может состоять из множества одинаковых (однородных, подобных) объектов. Например, объект «апельсин» состоит из частей — долек апельсина. Объект «школьный класс» состоит из множества учеников — мальчиков и девочек приблизительно одного возраста. Каждый ученик является целой, самостоятельной частью объекта «школьный класс».

Объект может состоять из множества различных объектов. Например, объект «компьютер» состоит из множества не похожих друг на друга объектов (системный блок, монитор, клавиатура и т. д.). При делении объекта «компьютер» на части новые объекты получают разные имена; признаки новых объектов различны.

При описании состава объектов в одних случаях речь идет о составе конкретного объекта, а в других — об общих составных частях множества объектов. В последнем случае описание состава содержит ответ на вопрос «Из чего обычно состоят объекты некоторого множества?». Например:

Описывая состав объекта, человек мысленно «разбирает» его на части. При этом, как правило, используют такой приём: сначала называют небольшое число крупных частей, затем каждую из них «разбирают» на части поменьше и т. д. Например, при описании состава дома удобно выделить сначала фундамент, стены и крышу, затем в составе стены выделить окно и дверь, затем сообщить, что окно состоит из рамы и стёкол, и так же поступить, описывая состав двери (рис. 10).

Схема отношений «входит в состав» (схема состава) отражает не только составные части, но и тот порядок, в котором предмет «разбирался» на части. Таким образом, она отражает строение (структуру) объекта. На схеме состава можно использовать линии без стрелок, если имя объекта-части располагать ниже имени объекта, которому принадлежит эта часть.

Все имена на рис. 11 — общие (обозначают множества предметов), потому что эта схема отражает состав не одного конкретного дома, а «дома вообще».

При описании признаков сложного, составного объекта человек может назвать не только действия и характеристики всего объекта, но также действия и свойства объектов-частей. Например, весь дом можно строить и ремонтировать, крышу — красить, а стекло — вставлять; весь дом имеет длину, ширину и высоту, стены — толщину, крыша — высоту.

Самое главное

В сообщении об объекте могут быть приведены не только признаки данного объекта, но и отношения, которые связывают его с другими объектами. Имя отношения обозначает характер этой связи. Отношения могут связывать не только два объекта, но и объект с множеством объектов или два множества.

В зависимости от ситуации объект может рассматриваться как единое целое либо «распадаться» на более мелкие объекты.

Объект может состоять из множества одинаковых (однородных, подобных) объектов или множества различных объектов.

Схема отношений «входит в состав» (схема состава) отражает не только составные части, но и тот порядок, в котором предмет «разбирался» на части.

Источник

Отношения. Часть I

Формальная теория моделирования использует алгебраические отношения, включая их в сигнатуры моделей алгебраических структур, которыми описывает реальные физические, технические и информационные объекты, процессы их функционирования. К числу последних я отношу, например, базы данных (реляционные базы данных (РеБД)). Не менее важной считаю область принятия решений, которая состоит из двух основных статистической и алгебраической, основанной целиком на теории отношений. Образовательный уровень специалистов в этой теории близок к нулю.

Откройте учебник по специализации и там увидите в лучшем случае об эквивалентностях, которые авторами трактуются весьма своеобразно. Одного защитившегося уже ДТН спрашиваю: Вы рассматриваете отношение эквивалентности на указывая ни носителя отношения, ни конкретного отношения, как оно у Вас выглядит в записи? Ответ: как выглядит — обыкновенно. Выясняется, что он обо всем этом имеет весьма смутное представление.

Публикаций по проектированию РеБД, кроме иностранных статей назвать затрудняюсь. В 90-х годах был оппонентом, писал отзыв на диссертацию, где рассматривались и иерархические, и сетевые, и реляционные БД. Но как-то год, полтора назад опять на отзыв пришла работа, автор пишет уже только о РеБД, о нормализации отношений БД, но теоретической новизны не показал. Во многих ВУЗах читается курс о базах данных, но не о том, как их создать, создать СУБД, а как правило, о том как эксплуатировать готовую (зарубежную) БД.

Преп. состав не готов научить специалистов IТ-шников создавать отечественные СУБД, ОS, языки программирования, я уж не говорю о БИС, СБИС, заказных БИС. Здесь, по-видимому, поезд ушел давно и надолго. Так что напрасно надуваются у некоторых щеки от гордости (читай снобизма) это видно по комментариям к чужим публикациям, покажите сами, что можете, а не балуйтесь никчемными переводами и перепевками чужого ради предмета гордости — «рейтинга» и «кармы». Сказывается не только отсутствие креатива, но простой образованности и воспитания.

Вторая предметная область неразрывно, связанная с отношениями, — принятие решений. Каждый из нас постоянно занят этим. Мы без решения осознанного или неосознанного пальцем не пошевелим. Мало кто понимает, а еще меньше пишет о решениях. В основе решения любого ЛПР (лица, принимающего решение) лежит предпочтение альтернатив. А моделью предпочтения как раз и является такой тип отношений, который назван «пространством отношений предпочтения». Но кто их изучает. Когда я пришел к «специалисту» по отношениям с вопросом о количестве отношений каждого типа, он не зная ответа, «убил» встречным вопросом, а зачем это Вам?

Понятие отношения

Думаю, что термин отношение знаком каждому читателю, но просьба дать определение поставит большинство в тупик. Причин для этого много. Они чаще всего в преподавателях, которые, если и использовали отношения в процессе преподавания, внимания на этом термине не заостряли, запоминающихся примеров, по-видимому, не приводили.

В моей памяти есть несколько на всю жизнь запомнившихся примеров. Об отображениях и об отношениях. Расскажу вначале об отображениях. Имеется два ведерка с краской. В одном белая в другом — черная. И есть коробка с кубиками (очень много). Грани имеют рельефные номера. Сколькими способами можно раскрасить грани кубиков в два цвета? Ответ неожиданный — столькими, сколько 6-разрядных двоичных чисел, или 2 6 = 64. Поясню подробнее ф: 2→6 отображаются 2 объекта в 6. Каждая строчка таблицы- дискретное отображение фi.

Построим таблицу с 6 колонками и краскам сопоставим число белая — нуль, черная — единица, а граням кубика колонки. Начинаем с того, что все 6 граней белые — это 6-мерный нулевой вектор. Вторая строчка одна грань черная, т. е. младший разряд заполнен 1. и так до исчерпания 6-разрядных двоичных чисел. Кубики ставим в общий длинный ряд. У каждого из них как бы появился номер от 0 до 63.

Теперь отображение наоборот. Пачка листов бумаги (много) и 6 красок (фломастеры).
Фломастерами разного цвета надо пометить обе стороны бумажных листов. Сколько листов потребуется. Ответ f: 6 → 2 или 6 2 =36. Речь идет о произвольных отображениях.

Получили 9 упорядоченных пар элементов из А×А, в паре первый элемент из первого сомножителя, второй — из второго. Теперь попробуем получить все подмножества из декартова квадрата А×А. Вначале простенький пример.

Подмножества будут содержать из А×А разное количество элементов (пар): одну, две, три и так до всех 9 пар, включаем в этот список и пустое множество (Ø). Сколько же получилось подмножеств? Много, а именно 2 9 = 512 элементов.

Определение. Любое подмножество декартова произведения (у нас квадрата) множества называется отношением. Заметим, в произведении используется одно и то же множество. Если множества разные, возникает не отношение, а соответствие.

Символ отношения ставится слева от элементов R(x, y) или между ними x R y; х, у є А.
Определение Множество всех подмножеств множества А называется булеаном. Наш булеан состоит из 2 |А×А| элементов, здесь|А×А| — мощность множества.

Отношения можно задавать в разном представлении над А=:

Рисунок 1.2. а)Матрица 4×4 бинарного отношения б) нумерация клеток Матрицы

Здесь используются номера клеток, заполненные единицами на рис. 1б)
— Векторное представление. Двоичный вектор для представления бинарного отношения формируется из элементов <0,1>следующим образом:

Рассмотренный пример задания отношения в векторной форме будет иметь следующий вид:

— Представление графом. Поставим в соответствие элементам множества
А = точки на плоскости, т.е. вершины графа G = [Q, R].

Проведем в графе дугу от (xi) к (xj) тогда и только тогда, когда пара (xi,xj) є R (при i = j дуга (xi,xi) превращается в петлю при вершине (xi). Пример (рис. 1а) представления бинарного отношения A[4×4] графом изображен на рис.2.2.

Рисунок 2.2. Представление отношения ориентированным графом

Каталог бинарных отношений (n = 3)

Большое видится на расстоянии. Чтобы почувствовать отношения их разнообразие, мощность мне пришлось вручную создать каталог бинарных отношений над множеством из 3-х элементов, который включил все (боле 500 отношений) отношения. После этого «дошло» или «зашло»об отношениях.

Очевидно, что в каталог войдут 2 3×3 = 2 9 отношений, и каждое из них снабдим набором присущих им свойств. Ниже (табл. 3) приводится полный список всех 512 отношений над множеством А, |A| = 3, из трех элементов. Приводятся также результаты подсчета количества отношений (табл. 2), представленных сочетаниями номеров клеток декартова квадрата 3×3, различных подклассов для различных значений мощности множества-носителя (n = 3). Для каждого отношения указаны его основные свойства и принадлежность типу (табл. 3). Сокращения, используемые в каталоге раскрываются таблицей 2
Таблица 2. Количественные характеристики каталога при разных n

Сущность производимых операций с отношениями и их технику удобно пояснять на примерах, которые особенно просты и понятны для бинарных отношений. В операциях могут участвовать, два и/или более отношений. Операции, выполняемые над отдельными отношениями – унарные операции. Например, операции обращения (получение обратного) отношения, взятие дополнения, сужение (ограничение) отношения. Как пользоваться каталогом поясним примером примером.

Пример 2. Рассмотрим строку Nпр =14 таблицы каталога. Она имеет вид

Первые 9 символов строки (справа от равенства) — это двоичный вектор, соответствующий сочетанию из 9 по 2, а именно, номер первой клетки (отсчет слева направо) номер 5-й клетки матрицы бинарного отношения, т.е. элементы а1а1= а2а2 =1. Это сочетание имеет порядковый номер Ncч = 4 и сквозной номер Nпр = 14 в списке всех отношений. В остальных позициях этой строки стоят либо нули, либо единицы. Нули свидетельствуют об отсутствии свойства, соответствующего названию колонки нуля, а единицы – наличие такого свойства у рассматриваемого отношения.

Свойства и количественные характеристики отношений

Рассмотрим наиболее важные свойства отношений, которые позволят в дальнейшем выделить типы (классы) отношений, применяющиеся в реляционных базах данных в теории выбора и принятия решений и других приложениях. Далее будем обозначать отношение символом [R,Ω]. R- имя отношения, Ω — множество-носитель отношения.

1. Рефлексивность. Отношение [R,Ω] называется рефлексивным, если каждый элемент множества находится в отношении R сам с собой (рис. 2.3). Граф рефлексивного БО имеет во всех вершинах петли (дуги), а матрица отношения содержит (Е) единичную главную диагональ.

Рисунок 2.3. Рефлексивное отношение

2. Антирефлексивность. Отношение [R,Ω] называется антирефлексивным, если ни один элемент из множества не находится в отношении R сам с собой (рис. 2.4). Антирефлексивные отношения называют строгими.

Рисунок 2.4. Антирефлексивное отношение

3. Частичная рефлексивность. Отношение [R,Ω] называется частично
рефлексивным, если один или более элементов из множества не находится в отношении R сам с собой (рис. 2.5).

4. Симметричность. Отношение [R,Ω] называется симметричным, если вместе с упорядоченной парой (х, у) отношение содержит и упорядоченную пару (у, х) (рис. 2.6).

7. Транзитивность. Отношение [R,Ω] называется транзитивным, если для всяких упорядоченных пар (х, у),(у, z) є R, в отношении R найдется упорядоченная пара (х, z) є R или если R×R⊆R (рис. 2.9).

8. Цикличность. Отношение [R,Ω] называется циклическим, если для его элементов найдется подмножество элементов , для которого можно выписать последовательность xiRxi+1R. RxjRxi. Такая последовательность называется циклом или контуром (рис. 2.10).

9. Ацикличность. Отношения, в которых отсутствуют контуры называются, ациклическими. Для ациклических отношений выполняется соотношение R k ∩R = Ø для любого k > 1 (рис. 2.11).

10. Полнота (связность). Отношение [R,Ω] называется полным (связным), если для любых двух элементов (у, z) є Ω один из них находится в отношении с другим (рис 2.12). Линейность. Линейные отношения – это минимально полные отношения.

Рисунок 2.12. Линейное отношение

Итак, нами установлено, что отношения, как математические объекты, обладают определенными свойствами, определение которых приведены ранее. В следующем пункте рассмотрим существо и проявление некоторых свойств:

Количественные соотношения таких дискретных пространств представляют большой как
теоретический, так и практический интерес. Ниже рассматриваются некоторые аспекты количественных характеристик, связанных со свойствами отношений разных типов.

Операции над отношениями

Как и большинстве систем счисления с отношениями выполняются операции:

Выше было введено понятие бинарного отношения, как подмножества упорядоченных пар декартова произведения множеств, а также были рассмотрены свойства отношений. Кроме того, были упомянуты бинарные отношения и матричное представление отношений. Рассмотрим теперь понятие отношения более подробно, кроме того, рассмотрим основные операции бинарных отношений, наиболее важные из всего их множества для отношений.

Для них должны выполняться следующие условия:

Унарные операции над отношениями

9. Двойственное отношение (P d ) к отношению Р – отношение, образованное всеми теми парами, которые принадлежат универсальному отношению и не принадлежат обратному отношению (дополнение к обратному):

Двойственное и обратное отношения в совокупности содержат все пары декартова произведения A×A и не имеют общих пар, они также как и отношения Р и P образуют разбиение A×A

Сужение (РА1). Отношение [R1, A1] называется сужением отношения [R, A] на множество Ω1, если Ω1⊆ Ω и R1=R∩Ω1×Ω1. Отношение РА1 на множестве А1 ⊆ А – отношение РА1 на множестве А1, образованное всеми теми парами, которые принадлежат отношению Р и одновременно входят в состав декартова произведения А1 × А1. Другими словами, РА1 – пересечение отношений Р и А1×А1. Пусть А1 = , тогда для отношений Р и Q в матричной форме отношения сужения будут иметь вид:

Операции, требующие не менее двух отношений – n-арные (n-местные). В таких операциях могут участвовать отношения только одинаковой арности. Примеры таких операций: пересечение, объединение, разность, симметрическая разность отношений и некоторые другие. Если в операции используется более чем два отношения, то она выполняется последовательно для двух первых, а затем для итогового отношения и третьего и т.д.

Иначе говоря, эти операции определены для двух отношений. При операциях над отношениями предполагается, что области задания отношений (операндов и результата) совпадают, арности отношений совпадают, и результатом операции снова является отношение той же арности. В качестве примеров будем рассматривать операции над бинарными отношениями P и Q, заданными на дискретном множестве
А = булевыми матрицами (нули в матрицу, как правило, не вписываются):

1. Пересечение (P ∩ Q) – отношение, образованное всеми теми парами элементов из А, которые входят в оба отношения, т.е. общие для P и Q,
P ∩ Q = <(ai aj) | ((ai aj) є P) & ((ai aj) є Q)>.

Матрица отношения P ∩ Q получается как булево пересечение матриц P и Q:

При отсутствии таких общих пар говорят, что пересечение отношений пусто, т.е. оно является нуль-отношением. Пересечением отношений R1 и R2 (R1∩R2 ) называется отношение, определяемое пересечением соответствующих подмножеств из А×А.

2. Объединение (PUQ). Объединением отношений R1 и R2 (R1UR2 ) называется отношение, определяемое объединением соответствующих подмножеств из А×А. Отношение, образованное всеми парами, составляющими или отношение P, или отношение Q, т.е. парами, принадлежащими хотя бы одному из отношений (связка ∨ — или объединительная)
P U Q = <(ai aj) | ((ai aj) є P) ∨ ( (ai aj) є Q)>.

Если в множестве А×А нет других пар, не вошедших в отношение PUQ, а пересечение их нулевое, то говорят, что отношения P и Q при объединении образуют полное отношение А×А, а их система – разбиение этого полного отношения. Объединение матриц отношений образуется как булева сумма матриц отношений:

3.Разность (P\Q) – отношение, образованное теми парами из Р, которые не входят в отношение Q
P\Q = <(ai aj) | ((ai aj) є P)&((ai aj)∉Q)>.

Разность для отношений в матричном представлении имеет вид

4. Умножение отношений. Упорядоченные пары, образующие отношения могут содержать одинаковые элементы, а могут и не содержать. Среди пар, имеющих в своем составе одинаковые элементы, выделим такие упорядоченные пары, которые назовем смежными (примыкающими) и которые имеют во второй паре 1-й элемент, а в первой паре 2-й элемент один и тот же. Определим произведение смежных пар как упорядоченную пару:
( ai ak)∙( ak aj) => (ai aj).

В терминах теории графов сказанное означает, что смежные пары образуют маршрут из точки (ai) в точку (aj) транзитом через точку (ak), состоящий из 2-х смежных дуг. Произведение этих дуг – третья дуга из точки (ai) в точку (aj), реализующая переход между крайними точками маршрута в том же направлении, минуя промежуточную точку (ak). Говорят, что дуга (ai aj) замыкает эти точки напрямую.

5. Симметрическая разность (P∆Q) – отношение, образованное теми парами, которые входят в объединение PUQ, но не входят в пересечение P∩Q. Другая форма определения объясняет название операции: P∆Q образовано теми упорядоченными парами, которые являются объединением разностей P\Q и Q\P. Таким образом, выражение для симметрической разности записывается двумя разными способами:
P∆ Q = (PU Q)\(P ∩ Q) = (P\Q)U (Q\P).

Матрица симметрической разности имеет вид:

Из последней записи следует, что операция симметрической разности допускает перестановку операндов, т. е. коммутативна.

5. Композиция или произведение (P∙Q) – отношение, образованное всеми парами, для которых выполняется:
P∙Q = <(ai aj)|((ai ak) є P) & ((ak aj) є Q)>.

Другими словами, каждая упорядоченная пара в результирующем отношении есть результат умножения смежных пар, из которых 1-я пара принадлежит первому сомножителю-отношению, 2-я – второму сомножителю-отношению. Операция композиции не коммутативна.

Композиция (Р◦Q) на множестве М – отношение R, заданное на том же множестве М, которое содержит пару (x, y), когда существует Z є M такое, что (x, z) є P и (z, y) є Q.

При матричном представлении отношений матрица композиции отношений равна булеву произведению матриц исходных отношений:

Частный случай композиции отношений – квадрат отношения.

Можно показать, используя индукцию, что n-я степень отношения определяется рекуррентно по формуле:P n =P n-1 ◦Р, это означает, что пара (x,y) є P n в том случае, когда в матрице Р существует цепочка элементов: такая, что (xi, xi+1)є P, 1 Литература

Источник