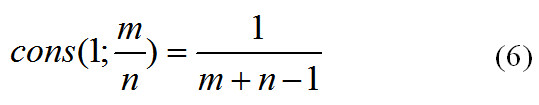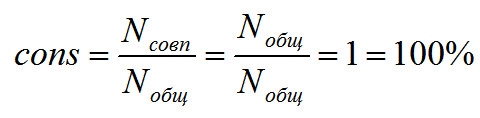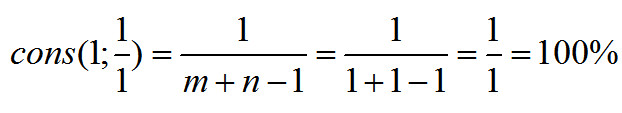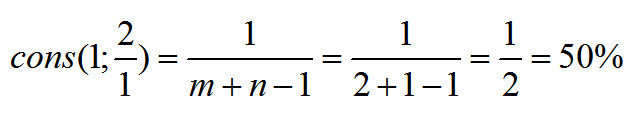Что такое совершенные консонансы и несовершенные консонансы
Что такое консонанс?
В предыдущей заметке мы выяснили, как устроен звук. Повторим ещё раз эту формулу:
ЗВУК = ОСНОВНОЙ ТОН + ВСЕ КРАТНЫЕ ОБЕРТОНА
Кроме того, как японцы любуются на цветение сакуры, полюбуемся и мы на график АЧХ — амплитудно-частотной характеристики звука (рис. 1):
Напомним, что по горизонтальной оси отложена высота звука (частота колебаний), а по вертикальной – громкость (амплитуда).
Каждая вертикальная линия – это гармоника, первая гармоника обычно называется основным тоном. Гармоники устроены так: вторая гармоника в 2 раза выше основного тона, третья – в три, четвертая – в четыре и так далее.
Краткости ради вместо «частота n-ой гармоники» будем говорить просто «n-ая гармоника», а вместо «частота основного тона» — «частота звука».
Итак, глядя на АЧХ, нам не составит труда ответить на вопрос, что же такое консонанс.
Как досчитать до бесконечности?
Консонанс буквально означает «со-звучие», совместное звучание. Что же у двух различных звуков может звучать совместно?
Нарисуем их на одном графике друг под другом (рис. 2):

Вот и ответ: часть гармоник могут совпадать по частоте. Логично предположить, что чем больше совпадающих частот, тем больше у звуков «общего», а, следовательно, тем больше консонанса в звучании такого интервала. Если быть совсем точным, то важно не просто число совпадающих гармоник, а то, какая доля от всех звучащих гармоник совпадает, то есть отношение числа совпадающих к общему числу звучащих гармоник.
Получаем самую простую формулу для подсчета консонанса:
где Nсовп — число совпадающих гармоник, Nобщ — общее число звучащих гармоник (количество различных звучащих частот), а cons и есть наш искомый консонанс. Если быть математически корректным, то величину лучше называть мера частотного консонанса.
Проблема заключается лишь в том, что и общее число гармоник и даже число совпадающих гармоник бесконечно.
Что же получится, если мы поделим бесконечность на бесконечность?
Поменяем масштаб предыдущего графика, «отдалимся» от него (рис. 3)
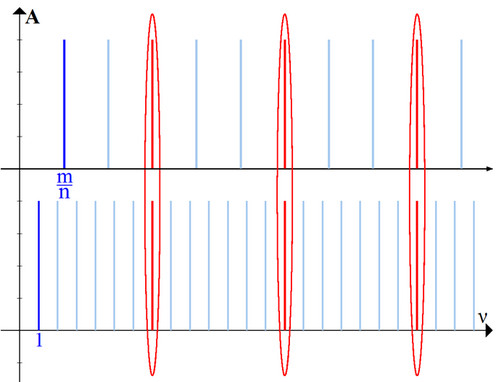
Мы видим, что совпадающие гармоники встречаются вновь и вновь. Картинка повторяется (рис. 4).
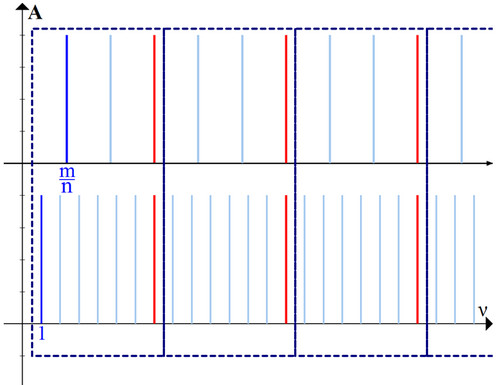
Это повторение нам и поможет.
Нам достаточно посчитать отношение (1) в одном из пунктирных прямоугольников (например, в первом), тогда из-за повторений и на всей прямой это соотношение останется таким же.
Для простоты частоту основного тона первого (нижнего) звука будем считать равной единице, а частоту основного тона второго звука запишем в виде несократимой дроби 
Заметим в скобках, что в нотных системах, как правило, используются именно звуки, соотношение частот которых выражается какой-либо дробью 



Посчитаем отношение (1) внутри первого прямоугольника (рис. 4).
Чему же равно общее число звучащих частот?
Будем рассуждать так.
Нужно учесть, что совпадающую частоту m мы опять посчитали два раза: когда считали частоты верхнего звука и когда считали частоты нижнего звука. Но фактически частота одна, и для правильного ответа одну «лишнюю» частоту нам нужно будет вычесть.
Итого всех звучащих частот внутри прямоугольника получится:
Подставив (2) и (4) в формулу (1), получим простое выражение для расчета консонанса:
Чтобы подчеркнуть, консонанс каких именно звуков мы рассчитали, можно указать эти звуки в скобках у cons:
С помощью такой простой формулы можно посчитать консонанс любого интервала.
А теперь рассмотрим некоторые свойства частотного консонанса и примеры его расчета.
Свойства и примеры
Для начала рассчитаем консонансы для самых простых интервалов и убедимся, что формула (6) «работает».
Какой интервал является самым простым?
Безусловно, прима. Две ноты звучат в унисон. На графике это будет выглядеть так:
Мы видим, что совпадают абсолютно все звучащие частоты. Следовательно, консонанс должен быть равен:
Теперь подставим соотношение для унисона 
Расчет совпадает с «интуитивным» ответом, что и следовало ожидать.
Возьмем другой пример, в котором интуитивный ответ так же очевиден, — октаву.
В октаве верхний звук в 2 раза выше нижнего (по частоте основного тона), соответственно, на графике это будет выглядеть так:
Из графика видно, что совпадает каждая вторая гармоника, и интуитивный ответ: консонанс равен 50%.
Посчитаем его по формуле (6):
И вновь расчетная величина равна «интуитивной».
Если возьмем в качестве нижнего звука ноту до и отложим на графике величину консонанса для всех интервалов внутри октавы (простых интервалов), то получим такую картину:

Самые высокие показатели меры консонанса у октавы, квинты и кварты. Они исторически относились к «совершенным» консонансам. Показатели малой и большой терций, и малой и большой секст чуть ниже, эти интервалы считаются «несовершенными» консонансами. Остальные интервалы имеют более низкую меру консонанса, традиционно они относятся к группе диссонансов.
Теперь перечислим некоторые свойства меры частотного консонанса, которые исходят из формулы для её расчета:
И m и n в формуле (6) находятся в знаменателе, следовательно, при увеличении этих чисел мера консонанса уменьшается.
Если сместить обе ноты на одинаковый интервал вверх или вниз (например, построить квинту не от ноты до, а от ноты ре), то соотношение 
Можно было бы привести и другие свойства консонанса, но пока ограничимся этими.
Физика и лирика
Рисунок 7 даёт нам представление о том, как устроен консонанс. Но так ли мы на самом деле воспринимаем консонанс интервалов? Существуют ли люди, которым не нравятся совершенные консонансы, а самые диссонантные созвучия кажутся приятными?
Да, такие люди, безусловно, есть. И для того, чтобы это объяснить, следует разграничить два понятия: физический консонанс и консонанс воспринимаемый.
Всё, что мы рассматривали в данной статье, имеет отношение к физическому консонансу. Для его расчета необходимо знать, как устроен звук, и как складываются разные колебания. Физический консонанс даёт предпосылки для консонанса воспринимаемого, но не обуславливает его на 100%.
Консонанс воспринимаемый определяется очень просто. Человека спрашивают, нравится ли ему данное созвучие. Если да – значит, для него это консонанс, если нет – диссонанс. Если ему дают на сравнение два интервала, то можно сказать, что один из них покажется человеку в данный момент более консонансным, другой менее.
Можно ли посчитать воспринимаемый консонанс? Даже если предположить, что можно, то расчет этот будет катастрофически сложным, в него будет входить ещё одна бесконечность – бесконечность человека: его опыт, особенности слуха и способности мозга. С этой бесконечностью так просто не справиться.
Однако исследования в этой области ведутся. В частности, композитор Иван Сошинский, любезно предоставляющий аудиоматериалы для данных заметок, разработал программу, с помощью которой можно для каждого человека построить его индивидуальную карту восприятия консонансов. Сейчас ведется разработка сайта mu-theory.info, на котором любой желающий сможет пройти тестирование и узнать особенности своего слуха.
И всё же, если есть воспринимаемый консонанс, и он отличается от физического, какой же смысл в расчете последнего? Можно переформулировать этот вопрос в более конструктивном ключе: как соотносятся эти два понятия?
Исследования показывают, что корреляция между усредненным воспринимаемым консонансом и физическим консонансом порядка 80%. Это означает, что у каждого человека могут быть свои индивидуальные особенности, но подавляющий вклад в определение консонанса вносит физика звука.
Разумеется, научные изыскания в этой области находятся ещё в самом начале. И в качестве структуры звука мы взяли сравнительно простую модель кратных гармоник, и расчет консонанса применяли самый простой – частотный, и не учитывали особенности деятельности мозга по обработке звукового сигнала. Но то, что даже в рамках таких упрощений получена очень высокая степень корреляции теории и эксперимента, весьма обнадеживает и дает стимул к дальнейшим исследованиям.
Применение научного метода в области музыкальной гармонии не ограничивается расчетом консонанса, оно дает и более интересные плоды.
Например, с помощью научного метода можно музыкальную гармонию изобразить графически, визуализировать. О том, как это сделать, мы поговорим в следующий раз.
Консонирующие и диссонирующие интервалы
Всякое двузвучие образует музыкальный интервал, обладающий (помимо своих звуковых качеств) еще и определенными акустическими свойствами, присущими только данному виду интервала и влияющими на характер его звучания.
По характеру звучания (или, иначе, фонизму), проявляющемуся наиболее ярко и выпукло в гармонических интервалах, последние как музыкальное явление подразделяются на две категории — консонансы и диссонансы.
Консонансами называются те интервалы, звуки которых на слух как бы сливаются друг с другом, образуя при этом мягкое (или относительно мягкое) и акустически устойчивое звучание, не требующее своего разрешения.
Диссонансами называются интервалы, звуки которых как бы противоречат друг другу и воспринимаются раздельно, то есть не сливаются в слуховом сознании воедино. Диссонансы звучат резче консонансов, по своей акустической природе они неустойчивы и требуют разрешения, то есть перевода их в консонанс.
Степень консонантности или диссонантности гармонических интервалов в значительной мере определяется наличием и яркостью (громкостью) звучания биений*
[Биением называется периодическое изменение интенсивности колебаний источника звука. Биения образуются в результате сложения двух гармонических колебаний, частоты которых близки по своим величинам.], возникающих между обертонами звуков, образующих данный интервал.
Так, например, при точной настройке между слышимыми обертонами звуков, образующих интервалы чистой примы и чистой октавы, биения отсутствуют вовсе. В интервалах чистой квинты и чистой кварты биения практически не слышны (то есть не воспринимаются человеческим слухом).
Интервалы терции и сексты уже дают ясно ощутимые биения, причем в больших терциях и секстах биения слышны слабеее, а в малых терциях и секстах — сильнее, но все же в целом они не нарушают консонантности интервала*
[Восприятие консонансов и диссонансов во многом зависит от регистра, а также от октавной удаленности звуков интервалов. Так, например, секста, взятая в низком регистре, звучит не вполне консонантно из-за множественных биений, возникающих между обертонами, которые у низких звуков значительно слышнее, чем у высоких.]
Консонансы подразделяются на три вида:
1) абсолютные консонансы, к которым относятся интервалы чистой примы и чистой октавы;
2) совершенные консонансы, к которым относятся чистая квинта и, отчасти, чистая кварта* [В эпоху полифонии строгого стиля в двухголосии кварта считалась диссонансом и использовалась лишь как задержание к терции или как проходящий звук.
В трех- и многоголосии кварта, помещенная внизу (например, в кварт-секстаккорде), то есть в непосредственном соседстве с басом, также считалась диссонирующим звуком, а в верхних голосах (например, в секстаккорде) допускалась как консонанс.] как взаимообращающийся с квинтой интервал;
3) несовершенные консонансы, к которым относятся большие и малые терции и большие и малые сексты.
Например, у малой септимы она значительно меньше, нежели у большой септимы. Наиболее же резким из всех диссонансов является малая секунда.
Разумеется, на характер звучания интервалов существенное влияние оказывают и другие факторы: регистр, расположение звуков данного интервала, тембровая сторона и т.д.
Так, в высоком регистре, где обертоны становятся гораздо менее слышимыми (или почти неслышимыми), характер звучания интервалов при прочих равных условиях просветляется, смягчается.
Наоборот, в нижнем регистре, где у каждого звука обертоны проявляются достаточно громко и вполне отчетливо воспринимаются на слух, те же интервалы приобретают совсем иной характер звучания — густой, насыщенный настолько, что порой становится затруднительно определять их на слух.
Последнее замечание в равной степени относится как к крайне низкому, так и к крайне высокому регистрам: в первом случае — из-за обилия и громкости звучания обертонов, а во втором — из-за почти полного отсутствия их.
В широком (и особенно ультрашироком) расположении интервалы (даже диссонирующие) предстают перед нами не в столь рельефном, как это было в тесном расположении и в среднем регистре, виде и звучат много мягче, поэтому труднее различаются на слух.
Нередко из-за яркости звучания обертонов при определении путают сами интервалы.
Например, интервал большой терции через три октавы (предположим, что это будут звуки ре большой октавы и фа-диез второй октавы) часто определяют как большую сексту ввиду того, что второй и пятый обертоны нижнего звука (или его третий и шестой частичные тоны) этого интервала (в данном случае это будут звуки ля малой и первой октав) слышны довольно громко и при недостаточно высоком уровне развития музыкального слуха могут быть приняты за основной тон интервала.
Особой спецификой обладают мелодические интервалы (в своей последовательности и образующие мелодию), звуки которых берутся порознь.
Именно в силу этого обстоятельства здесь трудно говорить о консонансах и диссонансах, ибо один реально звучащий тон не может быть ни консонансом, ни диссонансом.
И тем не менее благодаря свойству нашей памяти мы воспринимаем мелодические интервалы как некое единство и, по аналогии с гармоническими интервалами, подразделяем их на консонансы и диссонансы.
Однако, благодаря разновременности появления звуков мелодического интервала, диссонансы здесь оказываются предельно смягченными. Например, интервалы большой септимы и тритона, которые относятся к наиболее резким диссонансам, в мелодическом варианте звучат очень мягко.
Примером этого может служить начало дуэта Аиды и Радамеса из IV действия оперы «Аида» Дж. Верди, где указанные интервалы полностью соответствуют глубоко лирическому содержанию музыки:
Andantino Дж. Верди. Оп. «Аида», д. IV дуэт Аиды и Радамеса
Малая септима, тоже являющаяся диссонансом, в своем мелодическом облике звучит настолько мягко, что воспринимается почти как консонанс. Например:
Moderato А. Бородин. Оп. «Князь Игорь», д. I, к. 1, речитатив и песня Галицкого
И. Дунаевский. Песня о Волге из к/ф. «Волга-Волга»
Важными факторами также являются метрическое положение и ритмическая структура мелодического интервала.
Так, интервал, имеющий ямбическую формулу (то есть переход от слабой доли к более сильной), обычно звучит более напряженно, нежели интервал, имеющий хореическую формулу (переход от сильной к слабой доле), причем первый из этих двух типов мелодических интервалов чаще начинается с более короткой длительности и заканчивается более продолжительным звуком (или же оба будут одинаковыми по длительности), а второй — наоборот.
Само направление скачка в мелодическом интервале тоже имеет существенное значение. Так, например, восходящий скачок всегда содержит в себе более активный импульс, нежели нисходящий.
Все перечисленные выше факторы обычно подчеркивают соответствующие им стороны мелодического интервала, усиливая тем самым его выразительное значение в целом, что находит свое отражение и в творческой практике композиторов.
S o l F a theory
8. Интервалы: консонансы и диссонансы
По характеру звучания (фонизму) гармонические интервалы делятся на консонансы и диссонансы. Консонансами называются те интервалы, звуки которых на слух как бы сливаются и образуют мягкое (относительно мягкое) и акустически устойчивое звучание, не требующее разрешения.
Диссонансами называются те интервалы, звуки которых как бы противоречат друг другу и не сливаются в слуховом сознании воедино, требуют разрешения, т.е. перевода в консонанс.
Степень диссонантности или консонантности гармонических интервалов в значительной мере определяется наличием и яркостью звучания биений (периодическое изменение интенсивности колебания источника звука; образуются в результате сложения двух гармонических колебаний с близкими частотами, возникающих между обертонами звуков интервала.
У чистой примы и чистой октавы при точной настройке между слышимыми обертонами их нет. В чистой кварте и чистой квинте биения не воспринимаются человеческим слухом. Терции и сексты дают ощутимые биения (большие – меньше, малые – больше), но они не нарушают консонантности интервала.
Консонансы делятся на:
Восприятие консонансов и диссонансов зависит также от регистра и октавной удалённости звуков интервала. Так, секста в низком регистре звучит не вполне консонантно, так как биения у низких звуков гораздо слышнее, чем у высоких.
В высоком регистре характер звучания интервалов при прочих равных условиях смягчается, проясняется.
Все остальные интервалы – диссонансы (м. и б. 7, м. и б. 2, отчасти ч.4, все увеличенные и уменьшенные интервалы (большая часть из них – ладовые диссонансы)).
4 аспекта кон/диссонирования:
В ладовых системах европейской многоголосной музыки спад напряжения при переходе от диссонанса к консонансу (разрешении) создаёт особого рода ощущение удовлетворения, превращаясь в важный эстетический фактор. Чередование консонанса и диссонанса образует как бы «гармоническое» дыхание музыки.
Пифагорейцы относили к консонансам только октаву, квинту и кварту. В 13 веке к консонансам стали относить терцию, а затем и сексту. На рубеже 16-17 веков диссонансы стали вводиться без подготовки консонансами, на рубеже 19-20 веков диссонансы уже необязательно разрешаются в консонансы.
Последователи Пифагора различали консонансы и диссонансы в зависимости от числовых отношений тонов, последователи Аристоксена считали критерием консонантности «приятность» созвучий для слуха.
В XX веке градация сонантности осознаётся как многоступенная.
Гармонические и мелодические интервалы в музыке
Интервал в музыке – это сочетание двух звуков. Но сочетаться они могут по-разному: их можно сыграть или спеть одновременно или по очереди.
Гармонический интервал – это такой интервал, звуки которого берутся единовременно. Такие интервалы являются основой музыкальной гармонии, именно поэтому они имеют такое название.
Мелодический интервал – это интервал, в котором звуки берутся вразбивку: сначала один, затем второй. Из названия понятно, что такие интервалы рождают мелодии. Ведь любая мелодия представляет собой цепочку, в которой соединены несколько одинаковых или разных интервалов.
Мелодические интервалы могут быть восходящими (шаг от нижнего звука к верхнему) и нисходящими (переход от верхнего звука к более низкому).
Как различать интервалы на слух?
Гармонические и мелодические интервалы нужно уметь различать на слух. На уроках сольфеджио в музыкальных школах и колледжах даже практикуются специальные упражнения на слуховой анализ, когда учащимся играются разные созвучия, а они «отгадывают» что именно им сыграли. Но как это сделать?
Есть много разных способов, которые помогают запоминать звучание интервалов. Например, с детьми часто практикуют способ ассоциаций, когда звучание интервалов сравнивают с образами животных. Различать гармонические интервалы помогает знание их разделения на консонансы и диссонансы, а мелодические интервалы часто запоминают по начальным звукам известных песен.
Давайте рассмотрим каждый из названных способов отдельно.
Метод ассоциаций (интервалы и образы животных)
Итак, у нас есть восемь основных интервалов. Их звучание нужно как-то охарактеризовать. При этом часто привлекаются образы животных. Причем важными оказываются разные детали образов: то звуки животных, то их внешний вид – размер, цвет и т.д.
Можно предложить сделать эту творческую работу самому ребенку. В этом случае нужно просто сыграть ему все интервалы по порядку и параллельно спрашивать, какое животное можно нарисовать с помощью этих звуков. Допустимо, конечно, дать и готовое решение. Оно может быть примерно следующим (можно придумать что-то другое):
В дополнение мы предлагаем скачать вам наглядное пособие для занятий с детьми темой интервалов. В приложенном файле вы найдете картинки животных и соседствующие с ними нотные записи звучащих интервалов.
ИНТЕРВАЛЫ И ЖИВОТНЫЕ В КАРТИНКАХ ДЛЯ ДЕТЕЙ – СКАЧАТЬ
Консонансы и диссонансы в музыке
Все интервалы можно разделить на две большие группы – консонансы и диссонансы. Что это значит? Консонансы – это интервалы, которые звучат слаженно, красиво, звуки в них находятся в гармонии и ладу между собой. Диссонансы – это интервалы, которые, напротив, звучат резко, несогласно, звуки в них мешают друг другу.
Существует три группы консонансов: абсолютные, совершенные и несовершенные. К абсолютным консонансам относятся чистая прима и чистая октава – всего два интервала. Совершенными консонансами являются также два интервала – чистая квинта и чистая кварта. Наконец, к числу несовершенных консонансов принадлежат терции и сексты в своих разновидностях – они бывают малые и большие.
Если вы забыли, что такое чистые, большие и малые интервалы, то повторить и разобраться можно в статье «Количественная и качественная величина интервала».
К диссонирующим созвучиям относятся все секунды и септимы, а кроме того некоторые увеличенные и уменьшенные интервалы.
Как же различать интервалы на слух, зная о консонансах и диссонансах? Нужно помнить следующие характеристики и рассуждать логически:
Запоминаем интервалы по песням
Популярный способ запоминания интервалов – учить их по началу мелодий всем известных песен или произведений классической музыки. При этом не стоит забывать, что интервалы можно брать как вверх, так и вниз. И почти на каждый случай есть какой-нибудь пример. Конечно, не на всякий интервал можно подобрать песню, но для большинства простых интервалов это работает.
Вот, что мы рекомендуем для запоминания интонаций некоторых интервалов вверх и вниз:
Интервал
Чистая прима
Бетховен «К Элизе» или Моцарт «Симфония №40»
Большая секунда
Малая терция
Детская песня «Чижик-Пыжик»
Чистая кварта
Песня о дружбе «Дружба крепкая не сломается»
Малая секста
Песня из кинофильма «Бьют часы на старой башне»
Вот такие вот примеры очень могут помочь в освоении мелодических интервалов. С широких интервалов (септим и октав) вокальные мелодии начинаются очень редко, так как они являются неудобными для интонирования. Но их всегда можно распознать по характеру звучания или методом исключения.
Таким образом, в данном выпуске мы рассмотрели с вами целый «букет» очень важных вопросов, касающихся музыкальных интервалов: сравнили гармонические и мелодические виды интервалов, выяснили, какие способы могут помочь освоению интервалов на слух. В следующих выпусках мы продолжим рассказ об интервалах, рассмотрим их на ступенях мажора и минора. До новых встреч!