Что такое современная математика
Математика
Содержание
Основные сведения
Идеализированные свойства исследуемых объектов либо формулируются в виде аксиом, либо перечисляются в определении соответствующих математических объектов. Затем по строгим правилам логического вывода из этих свойств выводятся другие истинные свойства (теоремы). Эта теория в совокупности образует математическую модель исследуемого объекта. Таким образом первоначально, исходя из пространственных и количественных соотношений, математика получает более абстрактные соотношения, изучение которых также является предметом современной математики.
Традиционно математика делится на теоретическую, выполняющую углублённый анализ внутриматематических структур, и прикладную, предоставляющую свои модели другим наукам и инженерным дисциплинам, причём некоторые из них занимают пограничное с математикой положение. В частности, формальная логика может рассматриваться и как часть философских наук, и как часть математических наук; механика — и физика, и математика; информатика, компьютерные технологии и алгоритмика относятся как к инженерии, так и к математическим наукам и т. д. В литературе было предложено много различных определений математики (см. ниже).
Этимология
В текстах на русском языке слово «математика» или «мафематика» встречается по крайней мере с XVII века, например, у Николая Спафария в «Книге избранной вкратце о девяти мусах и о седмих свободных художествах» (1672 год) [5]
Определения
Одно из первых определений предмета математики дал Декарт [6] :
К области математики относятся только те науки, в которых рассматривается либо порядок, либо мера и совершенно не существенно, будут ли это числа, фигуры, звёзды, звуки или что-нибудь другое, в чём отыскивается эта мера. Таким образом, должна существовать некая общая наука, объясняющая всё относящееся к порядку и мере, не входя в исследование никаких частных предметов, и эта наука должна называться не иностранным, но старым, уже вошедшим в употребление именем Всеобщей математики.
Математика… наука о количественных отношениях и пространственных формах действительного мира.
Это определение Энгельса [8] ; правда, далее Колмогоров поясняет, что все использованные термины надо понимать в самом расширенном и абстрактном смысле.
Сущность математики… представляется теперь как учение об отношениях между объектами, о которых ничего не известно, кроме описывающих их некоторых свойств,— именно тех, которые в качестве аксиом положены в основание теории… Математика есть набор абстрактных форм — математических структур.
Приведём ещё несколько современных определений.
Герман Вейль пессимистически оценил возможность дать общепринятое определение предмета математики:
Вопрос об основаниях математики и о том, что представляет собой в конечном счёте математика, остаётся открытым. Мы не знаем какого-то направления, которое позволит в конце концов найти окончательный ответ на этот вопрос, и можно ли вообще ожидать, что подобный «окончательный» ответ будет когда-нибудь получен и признан всеми математиками.
Разделы математики
1. Математика как учебная дисциплина подразделяется в Российской Федерации на элементарную математику, изучаемую в средней школе и образованную дисциплинами:
и высшую математику, изучаемую на нематематических специальностях вузов. Дисциплины, входящие в состав высшей математики, варьируются в зависимости от специальности.
Программа обучения по специальности математика [13] образована следующими учебными дисциплинами:
2. Математика как специальность научных работников Министерством образования и науки Российской Федерации [14] подразделяется на специальности:
3. Для систематизации научных работ используется раздел «Математика» [15] универсальной десятичной классификации (УДК).
4. Американское математическое общество (AMS) выработало свой стандарт для классификации разделов математики. Он называется Mathematics Subject Classification. Этот стандарт периодически обновляется. Текущая версия — это MSC 2010. Предыдущая версия — MSC 2000.
Обозначения
Вследствие того, что математика работает с чрезвычайно разнообразными и довольно сложными структурами, система обозначений также очень сложна. Современная система записи формул сформировалась на основе европейской алгебраической традиции, а также математического анализа (понятия функции, производной и т. д.). Геометрия испокон века пользовалась наглядным (геометрическим же) представлением. В современной математике распространены также сложные графические системы записи (например, коммутативные диаграммы), нередко также применяются обозначения на основе графов.
Краткая история
Академиком А. Н. Колмогоровым предложена такая структура истории математики:
Развитие математики началось вместе с тем, как человек стал использовать абстракции сколько-нибудь высокого уровня. Простая абстракция — числа; осмысление того, что два яблока и два апельсина, несмотря на все их различия, имеют что-то общее, а именно занимают обе руки одного человека, — качественное достижение мышления человека. Кроме того, что древние люди узнали, как считать конкретные объекты, они также поняли, как вычислять и абстрактные количества, такие, как время: дни, сезоны, года. Из элементарного счёта естественным образом начала развиваться арифметика: сложение, вычитание, умножение и деление чисел.
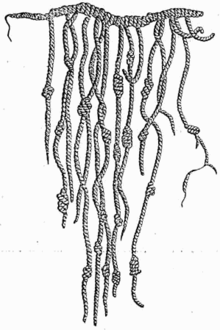
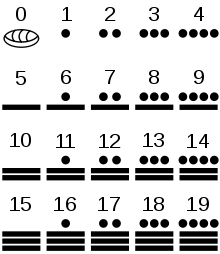
Развитие математики опирается на письменность и умение записывать числа. Наверно, древние люди сначала выражали количество путём рисования чёрточек на земле или выцарапывали их на древесине. Древние инки, не имея иной системы письменности, представляли и сохраняли числовые данные, используя сложную систему верёвочных узлов, так называемые кипу. Существовало множество различных систем счисления. Первые известные записи чисел были найдены в папирусе Ахмеса, созданном египтянами Среднего царства. Индская цивилизация разработала современную десятичную систему счисления, включающую концепцию нуля.
Исторически основные математические дисциплины появились под воздействием необходимости вести расчёты в коммерческой сфере, при измерении земель и для предсказания астрономических явлений и, позже, для решения новых физических задач. Каждая из этих сфер играет большую роль в широком развитии математики, заключающемся в изучении структур, пространств и изменений.
Философия математики
Цели и методы
Математика изучает воображаемые, идеальные объекты и соотношения между ними, используя формальный язык. В общем случае математические понятия и теоремы не обязательно имеют соответствие чему-либо в физическом мире. Главная задача прикладного раздела математики — создать математическую модель, достаточно адекватную исследуемому реальному объекту. Задача математика-теоретика — обеспечить достаточный набор удобных средств для достижения этой цели.
Содержание математики можно определить как систему математических моделей и инструментов для их создания. Модель объекта учитывает не все его черты, а только самые необходимые для целей изучения (идеализированные). Например, изучая физические свойства апельсина, мы можем абстрагироваться от его цвета и вкуса и представить его (пусть не идеально точно) шаром. Если же нам надо понять, сколько апельсинов получится, если мы сложим вместе два и три, — то можно абстрагироваться и от формы, оставив у модели только одну характеристику — количество. Абстракция и установление связей между объектами в самом общем виде — одно из главных направлений математического творчества.
Другое направление, наряду с абстрагированием — обобщение. Например, обобщая понятие «пространство» до пространства n-измерений. «Пространство 

Изучение внутриматематических объектов, как правило, происходит при помощи аксиоматического метода: сначала для исследуемых объектов формулируются список основных понятий и аксиом, а затем из аксиом с помощью правил вывода получают содержательные теоремы, в совокупности образующие математическую модель.
Основания
Вопрос сущности и оснований математики обсуждался со времён Платона. Начиная с XX века наблюдается сравнительное согласие в вопросе, что надлежит считать строгим математическим доказательством, однако отсутствует согласие в понимании того, что в математике считать изначально истинным. Отсюда вытекают разногласия как в вопросах аксиоматики и взаимосвязи отраслей математики, так и в выборе логических систем, которыми следует при доказательствах пользоваться.
Помимо скептического, известны нижеперечисленные подходы к данному вопросу.
Теоретико-множественный подход
Предлагается рассматривать все математические объекты в рамках теории множеств, чаще всего с аксиоматикой Цермело — Френкеля (хотя существует множество других, равносильных ей). Данный подход считается с середины XX века преобладающим, однако в действительности большинство математических работ не ставят задач перевести свои утверждения строго на язык теории множеств, а оперируют понятиями и фактами, установленными в некоторых областях математики. Таким образом, если в теории множеств будет обнаружено противоречие, это не повлечёт за собой обесценивание большинства результатов.
Логицизм
Данный подход предполагает строгую типизацию математических объектов. Многие парадоксы, избегаемые в теории множеств лишь путём специальных уловок, оказываются невозможными в принципе.
Формализм
Данный подход предполагает изучение формальных систем на основе классической логики.
Интуиционизм
Интуиционизм предполагает в основании математики интуиционистскую логику, более ограниченную в средствах доказательства (но, как считается, и более надёжную). Интуиционизм отвергает доказательство от противного, многие неконструктивные доказательства становятся невозможными, а многие проблемы теории множеств — бессмысленными (неформализуемыми).
Конструктивная математика
Основные темы
Числа
Понятие «число» первоначально относилось к натуральным числам. В дальнейшем оно было постепенно распространено на целые, рациональные, действительные, комплексные и другие числа.
| |||||||||||||||
 |  | ||||||||||||||
| Комплексные числа | Кватернионы | ||||||||||||||
 Числовые системы Числовые системы | |
|---|---|
| Счётные множества | Натуральные числа ( ) • Целые ( ) • Целые ( ) • Рациональные ( ) • Рациональные ( ) • Алгебраические ( ) • Алгебраические ( ) • Периоды • Вычислимые • Арифметические ) • Периоды • Вычислимые • Арифметические |
| Вещественные числа и их расширения | Вещественные ( ) • Комплексные ( ) • Комплексные ( ) • Кватернионы ( ) • Кватернионы ( ) • Числа Кэли (октавы, октонионы) ( ) • Числа Кэли (октавы, октонионы) ( ) • Седенионы ( ) • Седенионы ( ) • Альтернионы • Процедура Кэли — Диксона • Дуальные • Гиперкомплексные • Суперреальные • Гиперреальные • Surreal number (англ.) ) • Альтернионы • Процедура Кэли — Диксона • Дуальные • Гиперкомплексные • Суперреальные • Гиперреальные • Surreal number (англ.) |
| Другие числовые системы | Кардинальные числа • Порядковые числа (трансфинитные, ординал) • p-адические • Супернатуральные числа |
| См. также | Двойные числа • Иррациональные числа • Трансцендентные • Числовой луч • Бикватернион |
Преобразования
 |  |  |  |
| Арифметика | Дифференциальное и интегральное исчисление | Векторный анализ | Анализ |
 |  |  | |
| Дифференциальные уравнения | Динамические системы | Теория хаоса |
Структуры
Пространственные отношения
Более наглядные подходы в математике.
Дискретная математика
Дискретная математика включает средства, которые применяются над объектами, способными принимать только отдельные, не непрерывные значения.
 |  |  |  |
| Математическая логика | Теория вычислимости | Криптография | Теория графов |
Коды в системах классификации знаний
Онлайновые сервисы
Существует большое число сайтов, предоставляющих сервис для математических расчётов. Большинство из них англоязычные. [20] Из русскоязычных можно отметить сервис математических запросов поисковой системы Nigma.
Что такое современная математика
Когда я выбирала тему проекта, в первую очередь мне было интересно, где в жизни можно столкнуться с математикой, кроме уроков в школе.
В современном мире не возможно представить жизнь без бытовой техники, компьютеров, которые совершенствуются с каждым годом. На каждом шагу видим рекламу, магазины зазывают скидками, банки привлекают наше внимание сниженными кредитными ставками. Но как во всем этом разобраться? Где и как можно с экономить? Какие навыки и знания помогут мне ответить на эти вопросы?
Математика участвует в развитии интеллекта, мышления и личностных качеств человека. Формирует логический склад ума. Жизненные процессы и явления, можно описать на математическом языке, с помощью формул и математических законов. Человек, который знает язык математики, может правильно ориентироваться в окружающей нас действительности. Знание математики позволяет правильно обрабатывать информацию, статистические данные, делать правильные выводы. Если ученик будет уметь применять математический язык, то при ответе на уроке он сможет быстро и четко сформулировать и обосновать свой ответ.
Актуальность проекта: Получаем теоритические и практические знания, которые понадобятся в жизни. Расширяем свой кругозор, потому что математика встречается повсюду, в окружающем нас мире.
Цель проекта: проанализировать быт современного человека; определить где чаще всего он сталкивается в жизни с математикой; выяснить роль математики в жизни человека.
Задачи проекта: Изучить литературу по теме проекта; познакомится с краткой историей возникновения математики; понять где в современном образе жизни можно применять математику; найти примеры, где встречается математика в быту.
1. История возникновения математики
Считается, что люди учились считать и говорить одновременно.
Самые древние математические документы, которые дошли до нас – это хозяйственные записи вавилонян. Они сделаны за шесть тысяч лет до нашей эры. Спустя две тысячи лет в вавилонских клинописных таблицах можно встретить и хозяйственные расчеты, и настоящие математические задачи. Расцветом математики у вавилонян считается эпоха Самураи. В этот период можно увидеть сложные алгебраические действия, например, решение квадратных и кубических уравнений, которые сейчас умеют решать ученики десятых классов.
1.1.Возникновение арифметики и геометрии
Человек воспринимает математику, как понимание о количестве, структуре и соотношении. Начало развития математики – это создание практических навыков счета, измерения линий, поверхности, объемов. Понятие о натуральных числах появилось не сразу. Счет был вещественным — использовались пальцы, камешки, пометки. Потом стали считать пакетами единиц, в которых было, например, 10 объектов. С изобретением письменности стали применять буквы или особые обозначения для сокращённого изображения больших чисел. Названия чисел от двух до десяти, а также десятков и числа 100 в индоевропейских языках похожи. Из этого следует, что понятие абстрактного числа появилось очень давно, до разделения этих языков. У многих народов особое внимание уделяют числу 10, причиной был счет по пальцам.
В то же время, что и числа, человек начал изучать формы и фигуры. По наблюдениям приводил плоские и пространственные формы в одно. Обобщал их и присваивал названия похожие с оригиналами: например, у греков « ромбос » означает волчок, «трапедсион» — столик ( трапеция ), « сфера » — мяч.
Теория измерений была не точна и появилась значительно позже. Измерительным инструментом была мерная верёвка с узлами или пометками, что не могло приводить к точным измерениям. Определение площади происходило без инструментов.
1.2. Первые ученые-математики
Эвклида считали отцом геометрии. Множество теорем и гипотез были доказаны им. Он написал несколько научных трактатов. Из них два труда — «Элементы» и «Начала». Заложил основу всей европейской математики. В «Началах» содержится известная нам теорема Пифагора. По этому учебнику преподавали геометрию в школах Европы около 2 тысяч лет!
По возвращению в Европу написал ряд научных трудов, в том числе главный, по математике — «Книга абака». Леонардо ввёл в европейскую математику привычные нам арабские цифры, а также не менее привычную десятичную систему исчисления. Как истинный сын торговца, юноша внёс в математику понятие отрицательных чисел, называя их «долгом». Разработал основы бухгалтерского учёта. Об этом ученом я подробно рассказывала в своем предыдущем проекте «Числа Фибоначчи».
1.3. Интересные факты из математики.
Проверить подлинность купюры евро можно по серийному номеру буквы и одиннадцати цифр. Заменить букву на её порядковый номер в английском алфавите, сложить все получившиеся числа, складывать цифры результата, пока не получится одна цифра.
Цифра — 8, означает, что купюра подлинная. Ещё один способ проверки, складываем цифры, без буквы. Результат из буквы и одной цифры должен соответствовать определённой стране. Потому что евро печатают в разных странах. Например, для Германии это X2.
Слово «алгебра» одинаково звучит на всех языках мира. Оно – арабского происхождения, и ввел его в обиход великий математик Средней Азии конца 8 – начала 9 века Махаммед ибн Муса аль-Хорезми. Его математический трактат назывался «Альджебр валь мукабала», от первого слова которого и произошло международное название науки – алгебра.
Ноль «0» – единственное число, которое невозможно написать римскими цифрами.
2. Математика в современном мире.
Хочу рассказать о некоторых областях человеческой деятельности, где используется математика.
2.1. Математика вокруг нас.
Каждую минуту человек совершает какие-то действия: учит уроки, сдает экзамены, строит дом, делает ремонт, совершает покупки в магазине, рассматривает возможность приобретения жилья с помощью ипотеки, пишет компьютерные программы. Можно причислять бесконечно. Но некоторые моменты я рассмотрю в своем проекте.
Я и моя сестра стали взрослыми и родители решили сделать косметический ремонт в нашей комнате. Переклеить обои и поменять шторы. При обсуждении какие выбрать обои, было принято решение: обои должны быть без рисунков, светлых тонов, потому-то солнце в комнате только до обеда. Шторы, должны быть плотными, чтобы не пропускали яркий утренний свет.
Чтобы понять сколько надо купить обоев, клея, сколько понадобится метров ткани для пошива штор, в этом мне поможет математика. Для расчета количества необходимого материала для ремонта, понадобятся исходные данные: площадь стен комнаты, длина карниза и высота потолка. Для получения исходных данных я использовала измерительный инструмент – рулетку, длинной 5 метров. И полученные данные внесла в таблицы 1 и таблицу 2.
Наименование измеряемого материала
Общая площадь стен комнаты
Наименование измеряемого материала
После получения исходных данных необходимо решить где купить материал для ремонта? Для этого надо сравнить цены. Для сравнения я выбрала хозяйственный магазин и интернет магазин. Данные внесла в таблицу 3.
Цена в хозяйственном магазине
Цена в интернет магазине
Количество в таблице 3, было получено расчетным путем, используя исходные данные из таблиц 1 и 2.
После сравнения цен, сделан вывод – цена в интернет магазине на 7.23% ниже, чем в хозяйственном магазине.
В магазине вся мебель продается в разобранном виде. Покупатель может заказать сборку мебели на дому, стоимость которой составляет 20% от стоимости купленной мебели. Шкаф стоит 3800 рублей. Во сколько рублей обойдется покупка этого шкафа вместе со сборкой?
1) Пусть X – стоимость сборки мебели на дому
(рублей) – стоит сборка мебели на дому
2) (рублей) – стоимость шкафа вместе со сборкой.
10 : 100 = 0,1литра бензина на 1 км
6 * 46 = 276, стоимость 6 литров бензина
276 * 22 = 6072 рублей стоимость бензина на месяц по маршруту от дома до работы и обратно.
Цена = (10:100*60*46)*22= 6072 руб.
2.2. Математика в современных технологиях.
Строители, при возведении стен дома применяют теорему Пифагора, чтобы при строительстве соблюдалось возведение стен под прямым углом. Архитекторы, при проектировании зданий и сооружений, используют правило золотого сечения, которое основано на математическом ряде последовательных чисел Фибоначчи.
Одна таблетка лекарства весит 30 мг и содержит 14% активного вещества. Ребенку в возрасте до 6 месяцев врач прописывает 1,4 мг активного вещества на каждый килограмм веса в сутки. Сколько таблеток этого лекарства следует дать ребенку в возрасте четырех месяцев и весом 6 кг в течение суток?
30*0,14 = 4,2 мг, активного вещества в одной таблетке
1,4*6=8,4мг активного вещества назначил врач 6 месячного ребенка
8,4: 4,2 = 2 таблетки в сутки лекарства следует дать ребенку.
20 лет назад все расчеты производились вручную.
2.3. Самые востребованные профессии связанные с математикой.
Ученый – занимается изучением определенной области: физики, математики, биологии, на основе математических методов и экспериментов. Вносит свой вклад в науку. Деятельность ученого тесно связана с математикой. Без математических расчетов и применения некоторых математических законов не возможно доказать научные гипотезы и провести подготовительные мероприятия для проведения тестовой части научного исследования.
Инженер – специалист, изучающий техническую работу механических устройств. Его деятельность заключается в изучении информации, проверяет технические и экономические показатели. Ищет возможность сокращения производственного цикла. Математика для инженера является базой для инженерной работы специалиста.
Финансист – специалист в области финансовой деятельности. Контролирует распределение финансовых ресурсов. Работа построена на основе знаний математики. Часто используют в своей работе такие математические навыки как вычисление процентов, возведение в степень, умножение, вычитание, сложение, деление. Это самые простые математические функции, которые использует финансист.
Архитектор – специалист, который занимается архитектурным проектированием. Разрабатывает эскизные проекты, рабочие чертежи и рисунки. Для создания чертежей помогают знания по геометрии: теорема Пифагора, правило «золотого сечения», геометрические фигуры, измерение углов. Не возможно перечислить все математические законы, которые применяет в своей работе архитектор.
Программист – специалист, разрабатывающий программное обеспечение для вычислительно операционных систем. Создает исходный код для программ. Разрабатывает операционные системы для компьютеров, мобильные приложения, программы для электронных платежей, программы проектирования зданий и сооружений. Математика и программирование тесно связано. Без знаний дифференциальных уравнений, геометрии, алгебры, теории вероятности, программист не может работать.
В ходе исследовательской работы получила теоритические и практические навыки. Научилась самостоятельно замерять размеры жилого помещения, применив измерительный инструмент – рулетку 5метров. Участвовала в ремонте в моей комнате, что помогло на практике увидеть, как с помощью математики можно рассчитать количество необходимого материала. Выяснила, какие примерные задачи бывают на экзамене по математики в 11 классе. Узнала интересные факты о математики. Получила представление о специальностях, которые связаны с математикой.
После изучения литературы, решения задач, проделывания практических математических действий, можно сделать вывод по теме «Математика в современном мире». Расширила свой кругозор, получила понимание, что математика тесно связана с другими областями науки, выяснила, что все современные технологии основаны на математике, нашла примеры, где встречается математика.
Математика помогает сделать расчеты, прогнозировать конкретные ситуации вперед на определенный промежуток времени, создавать новые компьютерные программы, которые упростят работу ученых, инженеров, архитекторов, медиков и остальных.
Данную тему проекта можно использовать для выступлений на конференциях, перед одноклассниками. Можно продолжить работу с проектом, разделив на части и изучить более детально, каждое направление отдельно.
В современном мире математика помогает правильно обобщать, анализировать, находить закономерности, логически мыслить, быстро соображать при экстренных ситуациях и планировать свое время.
В своей работе использовала метод изучения теоритических и практических знаний по выбранной теме и анализ полученной информации.
Считаю данную тему актуальной и полезной.
Список используемой литературы
3. ЕГЭ 4000 задач с ответами по математике. – И.В.Ященко, И.Р.Высоцкий, А.В. Забелин, Москва, «Экзамен», 2015.