Что такое спектр радиосигнала
Что такое спектр радиосигнала
Спектр излучения радиосигнала — относительная интенсивность электромагнитного излучения по шкале частот.
Радиочастотный спектр — совокупность радиочастот в установленных Международным союзом электросвязи пределах, которые могут быть использованы для функционирования радиоэлектронных средств или высокочастотных устройств;
Совокупность гармонических электромагнитных колебаний, на которые можно разложить сложный сигнал, называется спектром этого сигнала. Различаютют амплитудно-частотный (АЧ) спектр и фазо-частотный (ФЧ) спектр. Для построения АЧ спектра на оси абсцисс откладываются частоты гармонических колебаний, образующих спектр, а по оси ординат из этих точек строятся перпендикулярные отрезки, длины которых соответствуют амплитудам соответствующих гармонических составляющих.
Физический смысл спектра заключается в том, что он определяет совокупность гармонических составляющих (с заданными амплитудами и частотами), формирующих заданную форму сигнала во временной области. В общем случае спектр сигналов, ограниченных во времени, бесконечен, т.е. для получения заданной формы сигнала необходимо бесконечно большое число гармоник, однако амплитуды гармоник падают с ростом частоты. Это позволяет ограничить реальный спектр некоторой полосой частот, достаточной для обеспечения воспроизведения сигналов с требуемой точностью. Диапазон
частот
(сокращенное наименование)
диапазона волн
Эти условные диапазоны спектра достаточно велики и, в свою очередь, разбиты на частотные диапазоны, куда входят так называемые радиовещательные и телевизионные диапазоны, диапазоны для наземной и авиационной, космической и морской связи, для передачи данных и медицины, для радиолокации и радионавигации и т.д.
Что такое спектр радиосигнала
Спектр излучения радиосигнала — относительная интенсивность электромагнитного излучения по шкале частот.
Радиочастотный спектр — совокупность радиочастот в установленных Международным союзом электросвязи пределах, которые могут быть использованы для функционирования радиоэлектронных средств или высокочастотных устройств;
Совокупность гармонических электромагнитных колебаний, на которые можно разложить сложный сигнал, называется спектром этого сигнала. Различаютют амплитудно-частотный (АЧ) спектр и фазо-частотный (ФЧ) спектр. Для построения АЧ спектра на оси абсцисс откладываются частоты гармонических колебаний, образующих спектр, а по оси ординат из этих точек строятся перпендикулярные отрезки, длины которых соответствуют амплитудам соответствующих гармонических составляющих.
Физический смысл спектра заключается в том, что он определяет совокупность гармонических составляющих (с заданными амплитудами и частотами), формирующих заданную форму сигнала во временной области. В общем случае спектр сигналов, ограниченных во времени, бесконечен, т.е. для получения заданной формы сигнала необходимо бесконечно большое число гармоник, однако амплитуды гармоник падают с ростом частоты. Это позволяет ограничить реальный спектр некоторой полосой частот, достаточной для обеспечения воспроизведения сигналов с требуемой точностью. Диапазон
частот
(сокращенное наименование)
диапазона волн
Эти условные диапазоны спектра достаточно велики и, в свою очередь, разбиты на частотные диапазоны, куда входят так называемые радиовещательные и телевизионные диапазоны, диапазоны для наземной и авиационной, космической и морской связи, для передачи данных и медицины, для радиолокации и радионавигации и т.д.
Что такое спектр радиосигнала
Введение
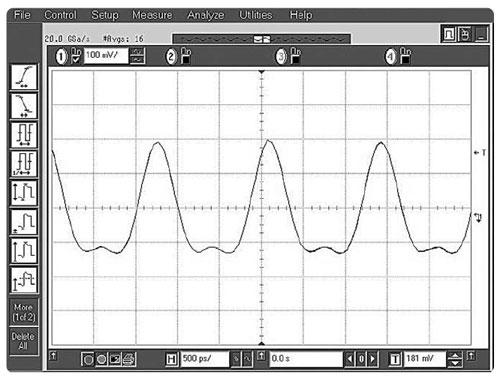
Рисунок 1-1. Сложный сигнал во временной области
Некоторые измерения требуют получения полной информации о сигнале – частоты, амплитуды и фазы. Такого рода анализ называется векторным анализом сигнала и рассматривается в документе Agilent Application Note 150-15, Vector Signal Analysis Basics. Современные анализаторы спектра способны проводить различного рода векторные измерения сигнала. Однако, другая обширная группа измерений не включает определения фазовых соотношений между синусоидальными составляющими. Такой тип анализа сигнала называется спектральным анализом. Поскольку спектральный анализ более прост для понимания и одновременно необычайно полезен на практике, мы сперва рассмотрим то, как анализаторы спектра осуществляют измерения для спектрального анализа, начиная с Главы 2.
Теоретически, чтобы осуществить преобразование из временной области в частотную область, сигнал должен быть оценен на всем промежутке времени, то есть до ± бесконечности. Однако, на практике мы всегда ограничиваемся каким-то конечным периодом, когда проводим измерение. Преобразование Фурье также может быть осуществлено и из частотной области во временную. В этом случае, опять же, теоретически нам надо знать все спектральные составляющие в диапазоне частот до ± бесконечности. На самом же деле, производя измерения только в той области частот, в которой содержится наибольшая часть энергии сигнала, можно получить вполне приемлемые результаты. При преобразовании Фурье из частотной области очень важно знать фазу индивидуальных составляющих. Например, прямоугольный периодический сигнал, переведенный в частотную область и обратно, может превратиться в пилообразный, если не были зафиксированы фазы.
Что такое спектр?
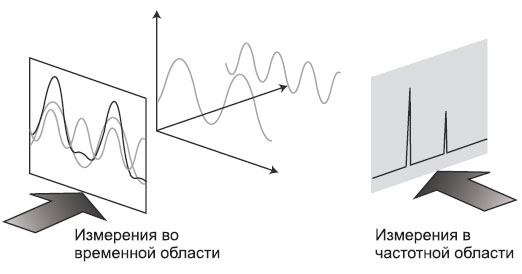
Так чем же является спектр в контексте нашего обсуждения? Спектр – это набор синусоидальных волн, которые, будучи надлежащим образом скомбинированы, дают изучаемый нами сигнал во временной области. На Рис. 1-1 показана волновая форма сложного сигнала. Давайте предположим, что мы ожидали увидеть чисто синусоидальный сигнал. И хотя форма явно демонстрирует нам, что сигнал не является чистой синусоидой, она не дает определенного ответа на вопрос о причинах данного явления. На Рис. 1-2 показан наш сложный сигнал во временной и в частотной области. В частотной области показана амплитуда для каждой синусоидальной волны в спектре в зависимости от частоты. Как видно, в данном случае спектр состоит лишь из двух волн. Теперь мы знаем, отчего наш сигнал не является чистой синусоидой: в нем содержится еще одна волна, вторая гармоника в нашем случае. Означает ли это, что измерения во временной области можно вообще не проводить? Отнюдь. Временная область является предпочтительной для многих измерений, а для некоторых является единственно возможной. К примеру, только во временной области можно измерить длительность фронта и спада импульса, выбросы и биения.
Рисунок 1-2. Связь между временной и частотной областью
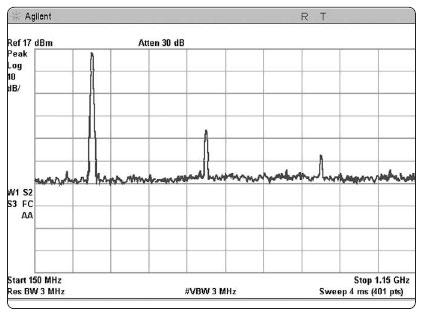
Рисунок 1-3. Тест передатчика на гармонические искажения
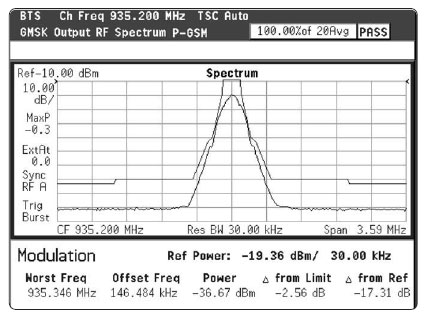
Рисунок 1-4. Радиосигнал GSM и спектральная маска, показывающая границу нежелательных выбросов
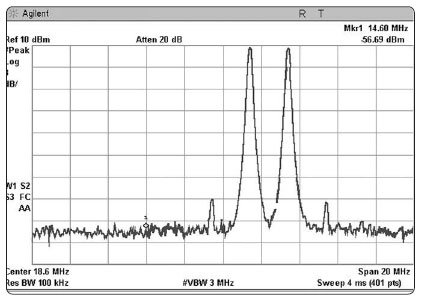
Рисунок 1-5. Двухтоновый тест радиочастотного усилителя мощности
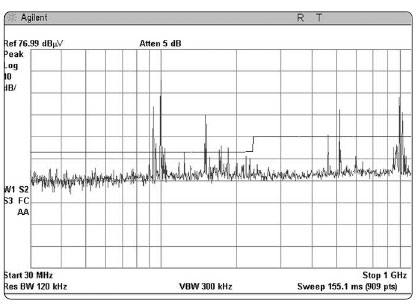
Рисунок 1-6. Выбросы излучения и их ограничения по стандарту CISPR11 как часть теста на электромагнитную совместимость
Типы измерений
Чаще всего анализаторами спектра измеряют частоту, мощность, модуляцию, искажения и шум. Знание спектрального состава сигнала очень важно, особенно в системах с полосой частот ограниченной ширины. Переданная мощность также является важным измеряемым параметром. Слишком малая мощность означает, что сигнал не сможет достичь точки назначения. Слишком большая мощность может быстро истощить заряд батарей, создать искажения и чрезмерно повысить рабочую температуру системы.
Измерение качества модуляции может быть важным для того, чтобы обеспечить нормальную работу системы и быть уверенным в том, что информация передается корректно. Измерения коэффициента модуляции, уровня полосы боковых частот, качества модуляции и заполнения полосы частот – это примеры самых распространенных тестов при аналоговой модуляции. В случае цифровой модуляции измеряются модуль вектора погрешности, дисбаланс IQ, зависимость погрешности фазы от времени и ряд других параметров. Более подробно об этих видах измерений рассказано в документе Agilent Application Note 150-15, Vector Signal Analysis Basics.
В сфере коммуникаций и связи измерение искажений очень важно как для приемников, так и для передатчиков. Излишние гармонические искажения на выходе передатчика могут создавать помехи на других коммуникационных частотах. В блоках предусилителей приемника не должно быть интермодуляции, чтобы избежать перекрестного наложения сигнала. Хороший пример – интермодуляция несущих сигналов кабельного телевидения, которые при распространении по распределительной системе вносят искажения в другие каналы этого же кабеля. Распространенными измерениями искажений являются измерения интермодуляции, гармоник и паразитного излучения.
Часто бывает нужно измерить и шум как сигнал. Любая активная цепь или устройство будет генерировать шум. Измерения коэффициента шума и отношения сигнал/шум (С/Ш) являются важными для описания показателей устройства и его вклада в общие показатели системы.
1 Жан Батист Фурье, 1768 – 1830, французский математик и физик, открывший, что периодические функции могут быть представлены последовательностью синусов и косинусов.
2 Если же сигнал появляется лишь раз, то его спектральным представлением будет непрерывное множество синусоидальных волн.
Страница: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Что такое спектр радиосигнала
 |
В зависимости от используемого окна полученный спектр имеет различный вид. На рисунке 2.38 показаны спектры синусоидального сигнала с частотой 50 Гц в зависимости от примененного окна. Появление на спектре составляющих рядом с основной частотой 50Гц вызвано эффектом просачивания, когда энергия основной составляющей распределяется между близлежащими спектральными полосами.
 |
В процессе цифрового интегрирования, при вычислении значений виброскорости и виброперемещения, на частотах ниже 10 Гц может появиться заметный шум, порождаемый процессом интегрирования или применением акселерометров с относительно высоким уровнем собственного шума. При измерении малых сигналов шум интегрирования может уменьшать динамический диапазон полезного сигнала. Особенно это касается измерений малых значений виброперемещения.
Методы спектрального анализа
Все методы спектрального анализа можно разделить на две группы. Классические методы, базирующиеся на использовании преобразований Фурье. Методы параметрического моделирования, в которых выбирается некоторая линейная модель формирующего фильтра и оцениваются его параметры. К первой группе относят корреляционный и периодограммный методы. Корреляционный метод выполняется на основе статистических методов обработки процесса вибрации.
Совокупность коэффициентов Ак и φк представляет амплитудный и фазовый частотные спектры периодического сигнала х(t). Графическое построение, наглядно интерпретирующее коэффициенты ряда Фурье, называется спектральной диаграммой.
Применяется для установления развития различных неисправностей. Особенно эффективно для анализа подшипников скольжения.
В линейных механических системах, частота возмущающей силы совпадает с частотой реакции системы на эту силу. Это позволяет идентифицировать источник вибрации. Большинство повреждений имеют жесткую связь с частотой вращения ротора механизма.
На высоких частотах вибрация приобретает волновой характер, в спектре мало линий, но достаточно малых сил для возбуждения вибрации. Эта зона определяет зарождение и развитие начальных стадий повреждений подшипников качения, зубчатых передач.
Вибрация ультразвуковых частот возбуждается, в основном, микроударами, но распространяется только по однородной среде (металл без болтов, сварных швов). До оптимальной точки ее измерения часто трудно добраться.
Спектральный сигнал может содержать следующие компоненты.
Амплитудно-частотная характеристика (АЧХ). Спектр сигнала.
При обсуждении переменного тока в одной из предыдущих статей (ссылка) мы познакомились с понятием гармонической (синусоидальной) функции. А бывают ли негармонические функции и сигналы и как с ними работать? В этом нам и предстоит сегодня разобраться 🙂 Кроме того, мы рассмотрим важнейшее понятие — амплитудно-частотную характеристику (АЧХ) сигналов.
Гармонические и негармонические сигналы.
Здесь A — амплитуда сигнала, w — циклическая частота, а \phi — начальная фаза. Вы спросите — а как же синус? Разве синусоидальный сигнал не является гармоническим? Конечно, является, дело в том, что sin\alpha = cos(\frac<\pi><2>\medspace-\medspace \alpha) — то есть сигналы отличаются начальной фазой, соответственно, синусоидальный сигнал не противоречит определению, которое мы дали для гармонических колебаний 🙂
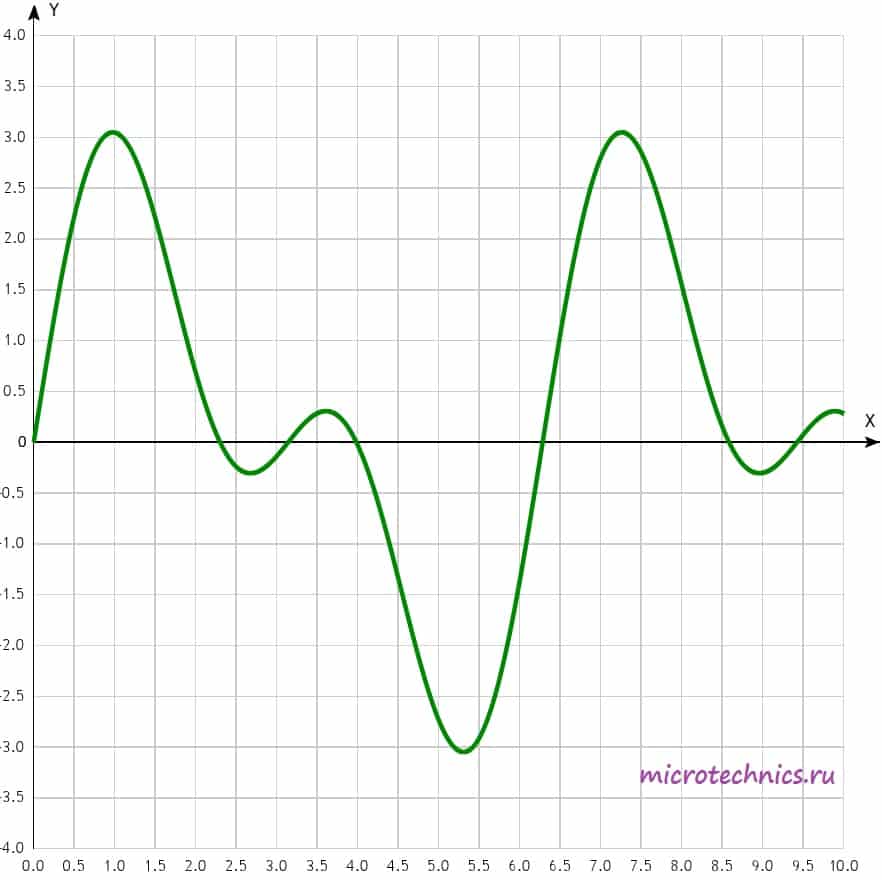
Вторым подклассом периодических сигналов являются негармонические колебания. Вот пример негармонического сигнала:
Как видите, несмотря на «нестандартную» форму, сигнал остается периодическим, то есть его форма повторяется через интервал времени, равный периоду.
Для работы с такими сигналами и их исследования существует определенная методика, которая заключается в разложении сигнала в ряд Фурье. Суть методики состоит в том, что негармонический периодический сигнал (при выполнении определенных условий) можно представить в виде суммы гармонических колебаний с определенными амплитудами, частотами и начальными фазами. Важным нюансом является то, что все гармонические колебания, которые участвуют в суммировании, должны иметь частоты, кратные частоте исходного негармонического сигнала. Возможно это пока не совсем понятно, так что давайте рассмотрим практический пример и разберемся чуть подробнее 🙂 Для примера используем сигнал, который изображен на рисунке чуть выше. Его можно представить следующим образом:
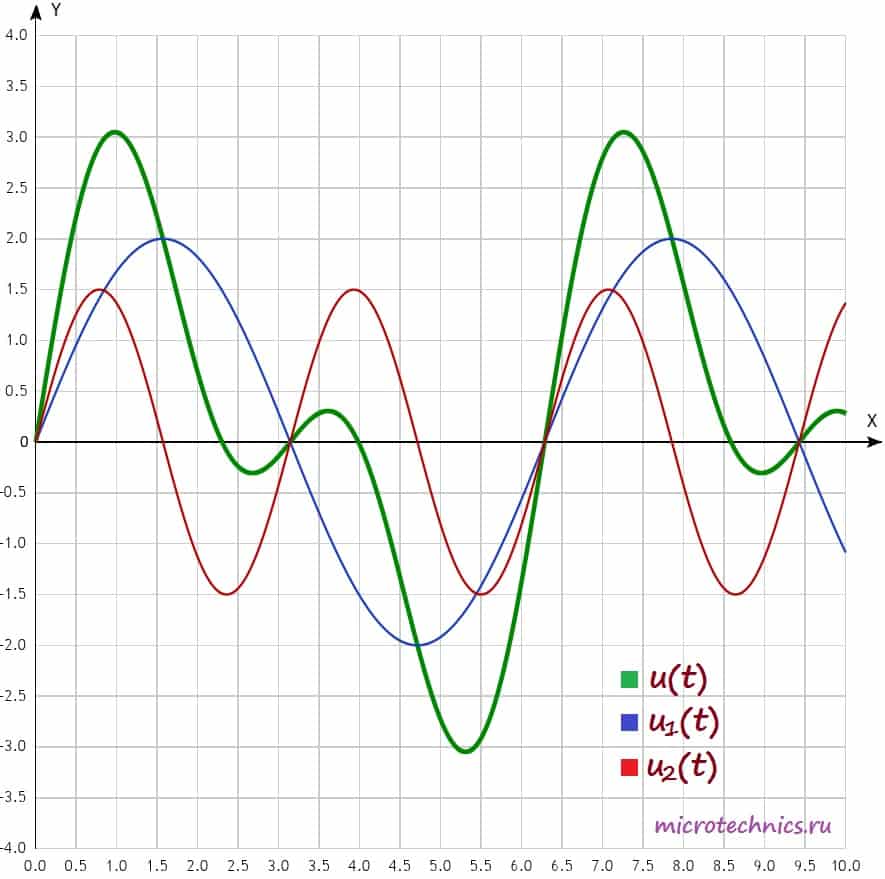
Давайте изобразим все эти сигналы на одном графике:
В этой формуле U_k — амплитуда, а \phi_k — начальная фаза k-ой гармоники. Как мы уже упомянули чуть ранее, частоты всех гармоник кратны частоте первой гармоники, собственно, это мы и видим в этой формуле 🙂 U_0 — это нулевая гармоника, ее частота равна 0, она равна среднему значению функции за период. Почему среднему? Смотрите — среднее значения функции синуса за период равно 0, а значит при усреднении в этой формуле все слагаемые, кроме U_0 будут равны 0.
Амплитудный спектр сигнала.
Совокупность всех гармонических составляющих негармонического сигнала называют спектром этого сигнала. Различают фазовый и амплитудный спектр сигнала:
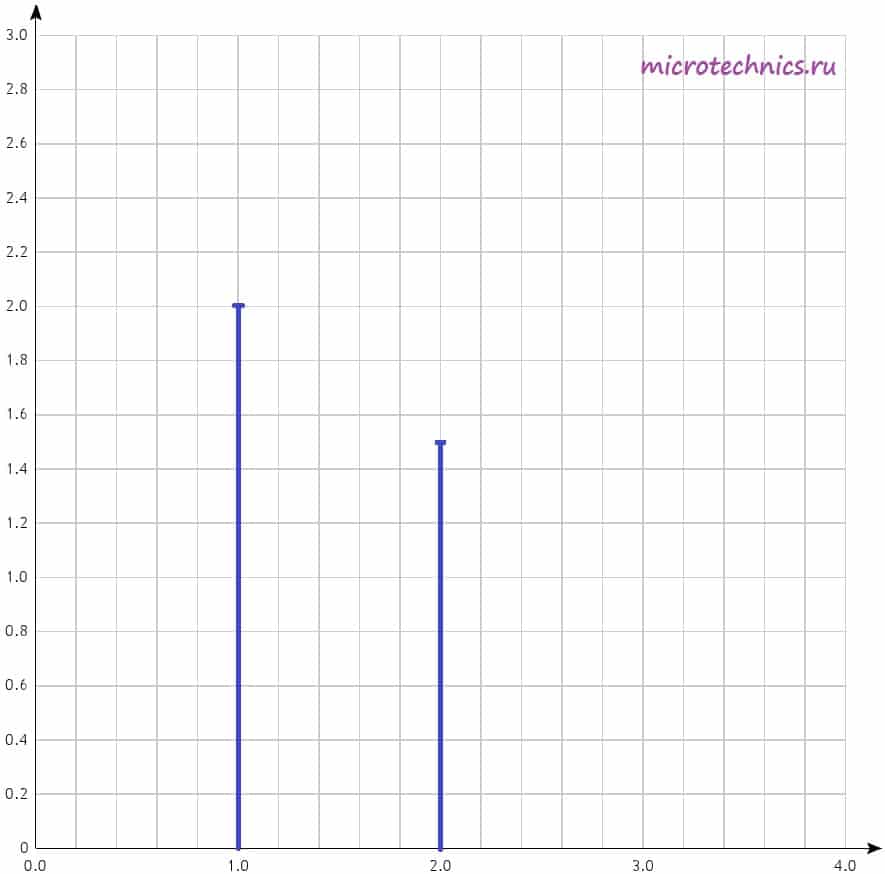
Давайте рассмотрим амплитудный спектр поподробнее. Для визуального изображения спектра используют диаграммы, представляющие из себя набор вертикальных линий определенной длины (длина зависит от амплитуды сигналов). На горизонтальной оси диаграммы откладываются частоты гармоник:
По горизонтальной оси могут откладываться как частоты в Гц, так и просто номера гармоник, как в данном случае. А по вертикальной оси — амплитуды гармоник, тут все понятно. Давайте построим амплитудный спектр сигнала для негармонического колебания, которое мы рассматривали в качестве примера в самом начале статьи. Напоминаю, что его разложение в ряд Фурье выглядит следующим образом:
У нас есть две гармоники, амплитуды которых равны, соответственно, 2 и 1.5. Поэтому на диаграмме две линии, длины которых соответствуют амплитудам гармонических колебаний. Фазовый спектр сигнала строится аналогично, за той лишь разницей, что используются начальные фазы гармоник, а не амплитуды.
Итак, с построением и анализом амплитудного спектра сигнала мы разобрались! Давайте перейдем к следующей теме сегодняшней статьи — к понятию амплитудно-частотной характеристики.
Амплитудно-частотная характеристика (АЧХ).
АЧХ является важнейшей характеристикой многих цепей и устройств — фильтров, усилителей звука и т. д. Даже простые наушники имеют свою собственную амплитудно-частотную характеристику. Что же она показывает?
АЧХ — это зависимость амплитуды выходного сигнала от частоты входного сигнала. Как мы выяснили в первой части статьи, негармонический периодический сигнал можно разложить в ряд Фурье. Но нас сейчас интересует, в первую очередь, аудио-сигнал, и выглядит он следующим образом:
Как видите, ни о какой периодичности здесь не идет и речи! Но, к счастью, существуют специальные алгоритмы, которые позволяют представить звуковой сигнал в виде спектра входящих в него частот. Мы сейчас не будем подробно разбирать эти алгоритмы, это тема для отдельной статьи 🙂 Просто примем тот факт, что они позволяют нам осуществить такое преобразование с аудио-сигналом.
Соответственно, мы можем построить диаграмму амплитудного спектра звукового сигнала. А пройдя через какую-либо цепь (к примеру, через наушники при воспроизведении звука) сигнал будет изменен. Так вот амплитудно-частотная характеристика как раз и показывает, какие изменения будет претерпевать входной сигнал при прохождении через ту или иную цепь. Давайте обсудим этот момент чуть поподробнее…
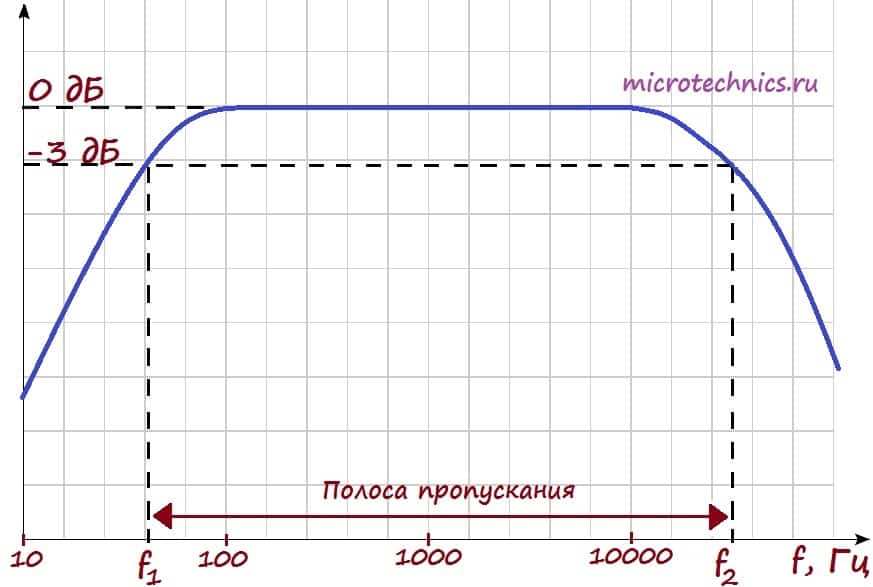
Итак, на входе мы имеем ряд гармоник. Амплитудная-частотная характеристика показывает, как изменится амплитуда той или иной гармоники при прохождении через цепь. Рассмотрим пример АЧХ:
Разберемся поэтапно, что же тут изображено… Начнем с осей графика АЧХ. По оси y мы откладываем величину выходного напряжения (или коэффициента усиления, как на данном рисунке). Коэффициент усиления мы откладываем в дБ, соответственно величина, равная 0 дБ, соответствует усилению в 1 раз, то есть амплитуда сигнала остается неизменной.
По оси x откладываются частоты входного сигнала. Таким образом, в рассматриваемом случае для всех гармоник, частоты которых лежат в интервале от 100 до 10000 Гц, амплитуда не изменится. А сигналы всех остальных гармоник будут ослаблены.
Практические примеры АЧХ аудио-устройств.
Частотный диапазон аудио-устройств обычно разбивают на низкие, средние и высокие частоты. Приблизительно это выглядит так:
Именно такую терминологию обычно можно встретить в разных программах-эквалайзерах, используемых для настройки звука. Теперь вы знаете, что красивые графики из таких программ являются именно амплитудно-частотными характеристиками, с которыми мы познакомились в сегодняшней статье 🙂
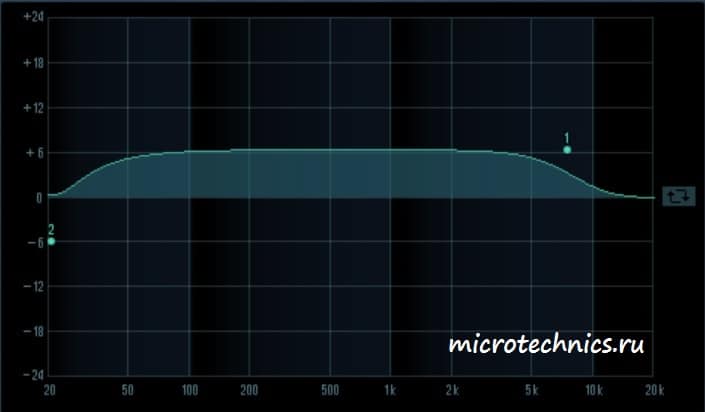
В завершении статьи посмотрим на пару АЧХ, полученных в программном эквалайзере:
Здесь мы можем видеть амплитудно-частотную характеристику усилителя. Причем усилены будут преимущественно средние частоты диапазона.
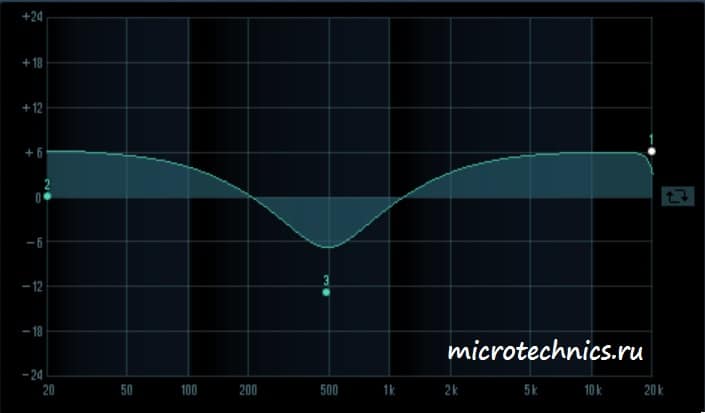
А здесь ситуация совсем другая — низкие и верхние частоты усиливаются, а в области средних частот для гармоник с частотой 500 Гц мы наблюдаем значительное ослабление.
А здесь усиливаются только низкие частоты. Аудио-аппаратура с такой АЧХ будет обладать высоким уровнем басов 🙂
На этом мы заканчиваем нашу сегодняшнюю статью… Спасибо за внимание и ждем вас на нашем сайте снова!