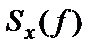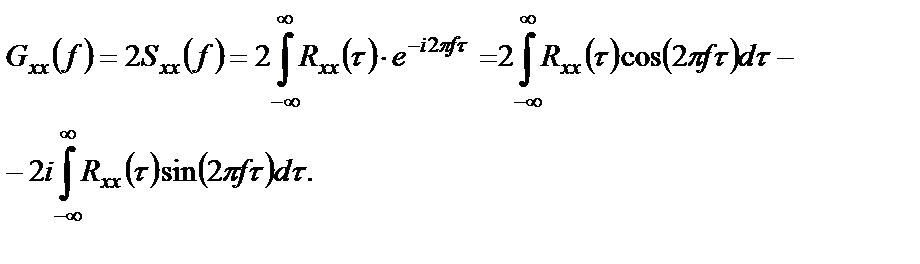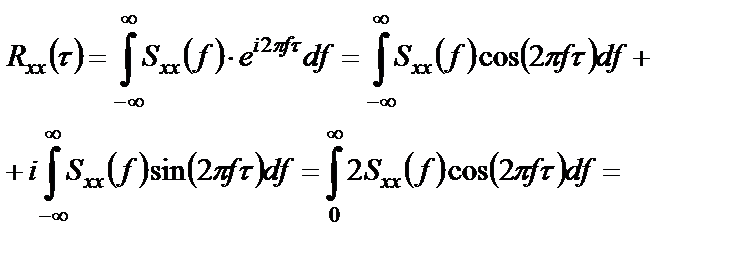Что такое спектральная мощность

Спектральная плотность мощности

Спектральная плотность мощности (СПМ) в физике и обработке сигналов — функция, задающая распределение мощности сигнала по частотам. Её значение имеет размерность мощности, делённой на частоту, то есть энергии.

Содержание

Формальное определение

Пусть — сигнал, рассматриваемый на промежутке времени . Тогда энергия сигнала на данном интервале равна:

= = = ,

где — спектральная функция сигнала. При , средняя мощность (дисперсия)

.

— спектральная плотность мощности (функция плотности спектра мощности).

Спектр плотности мощности сигнала сохраняет информацию только об амплитудах спектральных составляющих. Информация о фазе теряется. Поэтому все сигналы с одинаковым спектром амплитуд и различными спектрами фаз имеют одинаковые спектры плотности мощности.

Методы оценки

Оценка СПМ может выполняться методом преобразования Фурье, предполагающего получение спектра в области частот посредством быстрого преобразования Фурье (БПФ). До изобретения алгоритмов БПФ этот метод из-за громоздкости прямого вычисления дискретного преобразования Фурье (ДПФ) практически не использовался. Предпочтение отдавалось другим методам, в частности, методу корреляционной функции (Блэкмена-Тьюки) и периодограммному методу.

См. также

Литература

Полезное

Смотреть что такое «Спектральная плотность мощности» в других словарях:

Спектральная плотность мощности шума прибора СВЧ — 221. Спектральная плотность мощности шума прибора СВЧ Спектральная плотность мощности шума Noise spectral power density Pш Мощность шума прибора СВЧ в полосе 1 Гц Источник: ГОСТ 23769 79: Приборы электронные и устройства защитные СВЧ. Термины,… … Словарь-справочник терминов нормативно-технической документации

Спектральная плотность мощности шумового диода — 140. Спектральная плотность мощности шумового диода G Отношение среднего квадратического значения мощности шумового диода к заданному диапазону частот Источник: ГОСТ 25529 82: Диоды полупроводниковые. Термины, определения и буквенные обозначения… … Словарь-справочник терминов нормативно-технической документации

спектральная плотность мощности шума — spektrinis triukšmo galios tankis statusas T sritis radioelektronika atitikmenys: angl. noise spectral power density vok. Spektralleistungsdichte des Rauschens, f rus. спектральная плотность мощности шума, f pranc. densité spectrale de puissance… … Radioelektronikos terminų žodynas

спектральная плотность мощности излучения — spektrinis spinduliuotės galios tankis statusas T sritis Standartizacija ir metrologija apibrėžtis Pasirinktosios spektro dalies vienetinio dažnio, bangos ilgio (ar kito su jais susijusio dydžio) intervalo vidutinė spinduliuotės galios vertė.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

спектральная плотность мощности излучения — spektrinis spinduliuotės galios tankis statusas T sritis fizika atitikmenys: angl. radiation power spectral density vok. spektrale Strahlungsleistungsdichte, f rus. спектральная плотность мощности излучения, f pranc. densité spectrale de… … Fizikos terminų žodynas

относительная спектральная плотность мощности шума прибора СВЧ — Ндп. энергетический спектр шума энергетический спектр флуктуаций спектральная плотность шума ΔPш Отношение спектральной плотности мощности шума прибора СВЧ к выходной мощности в полосе 1 Гц. [ГОСТ 23769 79] Недопустимые, нерекомендуемые… … Справочник технического переводчика

Относительная спектральная плотность мощности шума прибора СВЧ — 222. Относительная спектральная плотность мощности шума прибора СВЧ Ндп. Энергетический спектр шума Энергетический спектр флуктуации Спектральная плотность шума Relative noise spectral power density ΔPш Отношение спектральной плотности мощности… … Словарь-справочник терминов нормативно-технической документации

Спектральная плотность — В статистической радиотехнике и физике при изучении детерминированных сигналов и случайных процессов широко используется их спектральное представление в виде спектральной плотности, которая базируется на преобразовании Фурье. Если процесс имеет… … Википедия

Спектральная плотность излучения — характеристика спектра излучения, равная отношению интенсивности (плотности потока) излучения в узком частотном интервале к величине этого интервала. Является применением понятия спектральной плотности мощности к электромагнитному излучению.… … Википедия

Спектральная плотность энергии (мощности) лазерного излучения — 5. Спектральная плотность энергии (мощности) лазерного излучения* Спектральная плотность энергии (мощности) СПЭ (СПМ) Wλ, Wv, Pλ, Pv Источник … Словарь-справочник терминов нормативно-технической документации

Источник

Однако в этой статье основное внимание уделяется ситуациям, в которых временные ряды известны (по крайней мере, в статистическом смысле) или непосредственно измерены (например, с помощью микрофона, производимого компьютером). Спектр мощности важен в статистическая обработка сигналов и в статистическом исследовании случайные процессы, а также во многих других отраслях физика и инженерное дело. Обычно процесс является функцией времени, но можно аналогичным образом обсудить данные в пространственной области, разлагаемые с точки зрения пространственная частота. [3]

Содержание

Объяснение

Любой сигнал, который можно представить как переменную, изменяющуюся во времени, имеет соответствующий частотный спектр. Сюда входят знакомые объекты, такие как видимый свет (воспринимается как цвет), музыкальные ноты (воспринимаются как подача), радио / ТВ (определяется их частотой, а иногда длина волны) и даже регулярное вращение земли. Когда эти сигналы рассматриваются в форме частотного спектра, выявляются определенные аспекты принимаемых сигналов или лежащие в основе процессы, их производящие. В некоторых случаях частотный спектр может включать отчетливый пик, соответствующий синусоидальная волна составная часть. И дополнительно могут быть пики, соответствующие гармоники основного пика, указывающего на периодический сигнал, который нет просто синусоидальный. Или непрерывный спектр может показывать узкие частотные интервалы, которые сильно усиливаются в соответствии с резонансами, или частотные интервалы, содержащие почти нулевую мощность, как если бы режекторный фильтр.

В физика, сигнал может быть волной, например электромагнитная волна, акустическая волна, или вибрация механизма. В спектральная плотность мощности (PSD) сигнала описывает мощность присутствует в сигнале как функция частоты на единицу частоты. Спектральная плотность мощности обычно выражается в Вт на герц (Вт / Гц). [4]

Когда сигнал определяется только с точки зрения Напряжениенапример, не существует уникальной мощности, связанной с указанной амплитудой. В этом случае «мощность» просто рассчитывается в единицах квадрата сигнала, так как это всегда будет пропорциональный к фактической мощности, передаваемой этим сигналом в данный сопротивление. Таким образом, можно использовать единицы V 2 Гц −1 для PSD и V 2 с Гц −1 для ОУР (спектральная плотность энергии) [5] даже при том, что никакая фактическая «мощность» или «энергия» не указана.

В общем случае единицы PSD будут отношением единиц отклонения на единицу частоты; так, например, серия значений смещения (в метрах) с течением времени (в секундах) будет иметь PSD в единицах m 2 / Гц. Для анализа случайной вибрации, единицы измерения грамм 2 Гц −1 часто используются для PSD ускорение. Здесь грамм обозначает перегрузка. [7]

Математически нет необходимости назначать физические размеры сигналу или независимой переменной. В следующем обсуждении значение х (т) останется неопределенным, но предполагается, что это независимая переменная времени.

Определение

Спектральная плотность энергии

Спектральная плотность энергии наиболее подходит для переходных процессов, то есть импульсных сигналов, имеющих конечную общую энергию. Конечное или нет, Теорема Парсеваля [9] (или теорема Планшереля) дает нам альтернативное выражение для энергии сигнала:

Икс ^ ( ж ) = ∫ − ∞ ∞ е − я 2 π ж т Икс ( т ) d т < displaystyle < hat > (е) = int _ <- infty>^ < infty>e ^ <- i2 pi ft>x (t) dt>

Спектральная плотность мощности

Тогда спектральная плотность мощности просто определяется как подынтегральное выражение выше. [11] [12]

Источник

Спектральные плотности некоторых сигналов

DSPL-2.0 — свободная библиотека алгоритмов цифровой обработки сигналов

Распространяется под лицензией LGPL v3

Спектральная плотность прямоугольного импульса равна:

Рассмотрим треугольный импульс длительности и амплитуды :

Для рассмотрения спектральной плотности треугольного импульса мы не будем вычислять интеграл Фурье непосредственно, потому что это потребует громоздких выкладок, а воспользуемся свойством преобразования Фурье свертки двух сигналов.

Можно заметить, что треугольный импульс длительности и амплитуды может быть представлен как результат свертки прямоугольного импульса длительности и амплитуды c самим собой, как это показано на рисунке 3.

Таким образом, мы можем применить свойство преобразования Фурье свертки сигналов и записать спектральную плотность треугольного импульса как квадрат спектральной плотности прямоугольного импульса длительности и амплитуды :

Гауссов импульс задается выражением:

График гауссова импульса при различном значении и показан на рисунке 4а.

Рассмотрим спектральную плотность гауссова импульса:

График спектральной плотности гауссова импульса для различного значения параметра показан на рисунке 4б. C увеличением увеличивается ширина гауссова импульса во временно́й области, и сужение спектральной плотности. При этом, убывание импульса во времени и по частоте носит экспоненциальный характер.

Как можно видеть из рисунка 5а, увеличение параметра приводит к сужению импульса во временно́й области.

Рассмотрим спектральную плотность двустороннего экспоненциального импульса:

Рассмотрим теперь односторонний экспоненциальный импульс, который получается из двустороннего при обнулении значения отрицательной полуоси времени:

Спектральная плотность одностороннего экспоненциального импульса равна:

Для получения спектральной плотности сигнала воспользуемся свойством двойственности преобразования Фурье, рассмотренным в в предыдущем параграфе. Тогда из выражения (2) можно записать:

В данном разделе мы рассмотрели спектральные плотности некоторых непериодических сигналов: прямоугольного, треугольного, гауссова импульса, а также одностороннего и двустороннего экспоненциальных импульсов.

Были приведены аналитические выражения для спектральных плотностей каждого из сигналов, а также их частотные свойства.

Источник

Спектральная плотность излучения

Спектральная плотность излучения — характеристика спектра излучения, равная отношению интенсивности (плотности потока) излучения в узком частотном интервале к величине этого интервала. Является применением понятия спектральной плотности мощности к электромагнитному излучению.

Энергия светового пучка неравномерно распределена по волнам различных длин. Зависимость частоты от длины волны описывается как λv=c

Для характеристики распределения излучения по частотам используют интенсивность, приходящуюся на единичный интервал частот. Эта величина называется спектральной плотностью интенсивности излучения и обозначается как I(v).

Различным видимым цветам соответствуют различные спектральные плотности видимого света.

Источники

Полезное

Смотреть что такое «Спектральная плотность излучения» в других словарях:

спектральная плотность излучения — spektrinis spinduliuotės tankis statusas T sritis fizika atitikmenys: angl. spectral density of radiation vok. Spektralstrahlungsdichte, f rus. спектральная плотность излучения, f pranc. densité spectrale de rayonnement, f … Fizikos terminų žodynas

спектральная плотность излучения — Энергия излучения, рассчитанная на единицу спектрального интервала. Примечание. Различают также спектральную плотность потока частиц и спектральную плотность потока квантов излучения … Политехнический терминологический толковый словарь

относительная спектральная плотность излучения — Отношение среднего значения оптической величины в рассматриваемом малом спектральном интервале к ширине этого интервала. [ГОСТ 25066 91] Тематики индикаторы знакосинтезирующие … Справочник технического переводчика

относительная спектральная плотность излучения — 8 относительная спектральная плотность излучения: Отношение среднего значения оптической величины в рассматриваемом малом спектральном интервале к ширине этого интервала. Источник: ГОСТ 25066 91: Индикаторы знакосинтезирующие. Термины,… … Словарь-справочник терминов нормативно-технической документации

Спектральная плотность мощности — Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей. Спектральная плотность мощности (СПМ) в физике и обработке сигналов функция, задающая распределение мощно … Википедия

Спектральная плотность — В статистической радиотехнике и физике при изучении детерминированных сигналов и случайных процессов широко используется их спектральное представление в виде спектральной плотности, которая базируется на преобразовании Фурье. Если процесс имеет… … Википедия

СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ — величины, характеризующей излучение (напр., потока излучения, силы света), отношение рассматриваемой величины, взятой в бесконечно малом спектр. интервале, содержащем данную длину волны l, к ширине этого интервала dl. Вместо l могут… … Физическая энциклопедия

Спектральная плотность энергии (мощности) лазерного излучения — 5. Спектральная плотность энергии (мощности) лазерного излучения* Спектральная плотность энергии (мощности) СПЭ (СПМ) Wλ, Wv, Pλ, Pv Источник … Словарь-справочник терминов нормативно-технической документации

спектральная плотность средней мощности оптического излучения ПОМ — 81 спектральная плотность средней мощности оптического излучения ПОМ [волоконно оптического лазера]: Средняя мощность оптического излучения передающего оптоэлектронного модуля [волоконно оптического лазера], приходящаяся на единичный интервал… … Словарь-справочник терминов нормативно-технической документации

спектральная плотность энергии излучения — spektrinis spinduliuotės energijos tankis statusas T sritis Standartizacija ir metrologija apibrėžtis Pasirinktosios spektro dalies vienetinio dažnio ar bangos ilgio intervalo vidutinė spinduliuotės energijos vertė. atitikmenys: angl. spectral… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

Источник

Спектральная плотность мощности

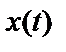
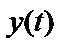
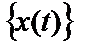
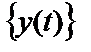
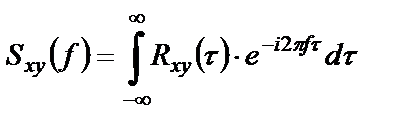
Взаимная спектральная плотность мощности(взаимный спектр мощности) двух реализаций и стационарных эргодических случайных процессов и определяется как прямое преобразование Фурье над их взаимной ковариационной функцией

(1.32)

или, с учетом соотношения между круговой и циклической частотами ,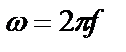

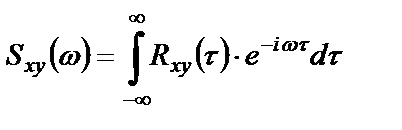
. (1.33)

Обратное преобразование Фурье связывает взаимные ковариационную функцию и спектральную плотность мощности:

. (1.34)

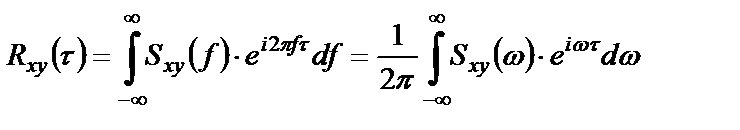
Аналогично (1.32), (1.33) вводится спектральная плотность мощности(спектр мощности) случайного процесса

(1.35)

. (1.36)

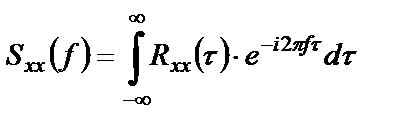
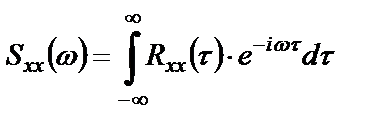
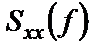
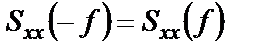
Функция обладает свойством четности:

. (1.37)

Для взаимной спектральной плотности справедливо следующее соотношение:

, (1.38)

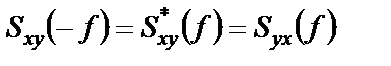
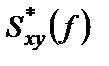
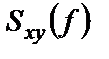
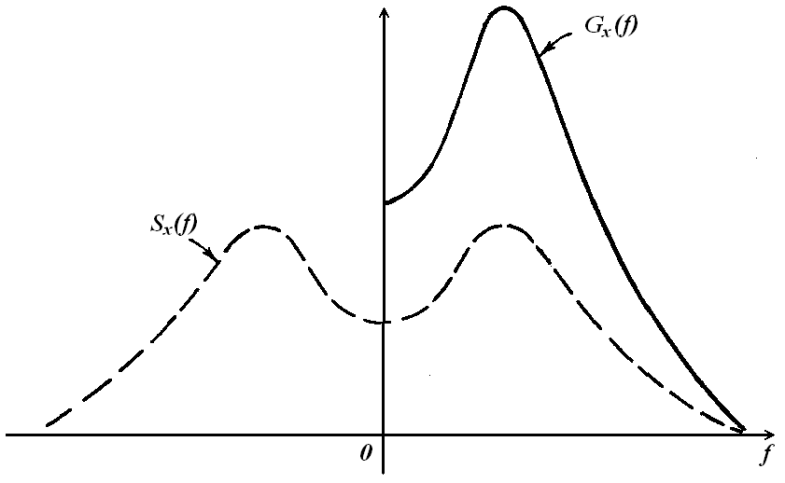
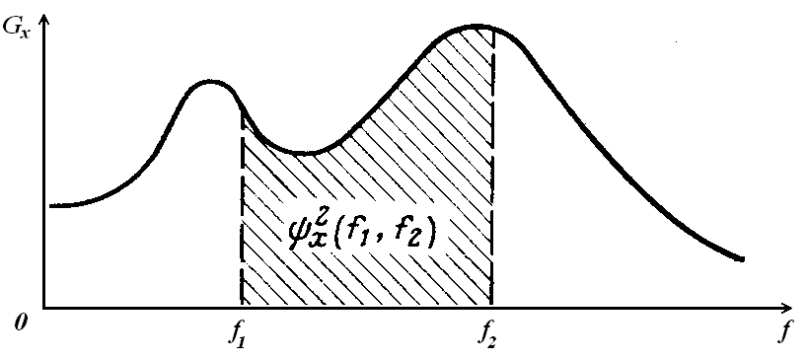
где – функция, комплексно сопряженная к .

Введенные выше формулы для спектральных плотностей определены как для положительных, так и для отрицательных частот и носят название двухсторонних спектральных плотностей. Они удобны при аналитическом изучении систем и сигналов. На практике же пользуются спектральными плотностями, определенными только для неотрицательных частот и называемыми односторонними (рисунок 1.14):

(1.39)

(1.40)

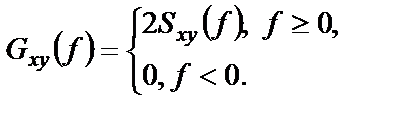
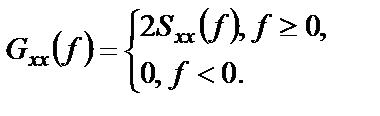
Рисунок 1.14 – Односторонняя 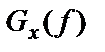и двусторонняя

Выведем выражение, связывающее одностороннюю спектральную плотность стационарного СП с его ковариационной функцией:

Учтем свойство четности для ковариационной функции стационарного СП и функции косинус, свойство нечетности для функции синус, а также симметричность пределов интегрирования. В результате второй интеграл в полученном выше выражении обращается в нуль, а в первом интеграле можно сократить вдвое пределы интегрирования, удвоив при этом коэффициент:

. (1.41)

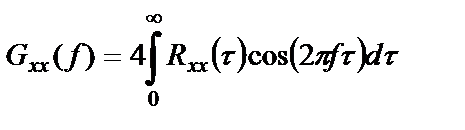
Очевидно, что спектральная плотность мощности случайного процесса 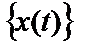является действительной функцией.

Аналогично можно получить обратное соотношение:

. (1.42)

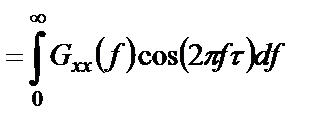
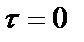
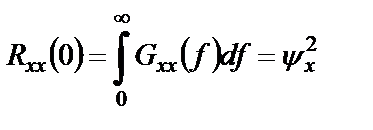
Из выражения (1.42) при следует, что

. (1.43)

Это означает, что общая площадь под графиком односторонней спектральной плотности равна среднему квадрату случайного процесса. Другими словами, односторонняя спектральная плотность интерпретируется как распределение среднего квадрата процесса по частотам.

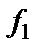
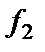
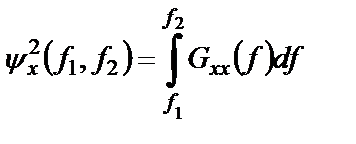
Площадь под графиком односторонней плотности, заключенная между двумя произвольными значениями частоты и , равна среднему квадрату процесса в этой полосе частот спектра (рисунок 1.15):

. (1.44)

Рисунок 1.15 – Свойство спектральной плотности

Взаимная спектральная плотность мощности является комплексной величиной, поэтому ее можно представить в показательной форме записи через модуль и фазовый угол:

, (1.45)

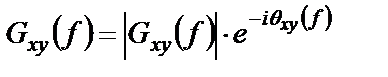
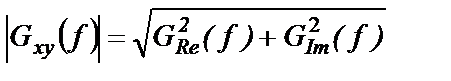
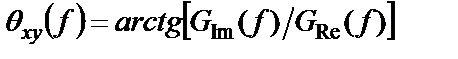
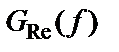
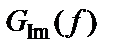
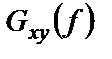
где – модуль;

– фазовый угол;

, – действительная и мнимая части функции соответственно.

Модуль взаимной спектральной плотности входит в важное неравенство

. (1.46)

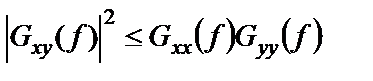
Это неравенство позволяет определить функцию когерентности (квадрат когерентности), которая аналогична квадрату нормированной корреляционной функции:

, (1.47)

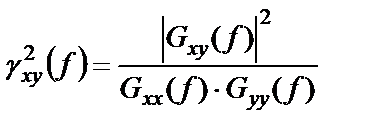
причем .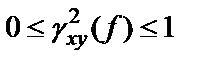

Второй способ введения спектральных плотностей состоит в непосредственном преобразовании Фурье случайных процессов.

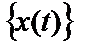
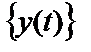
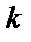
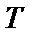
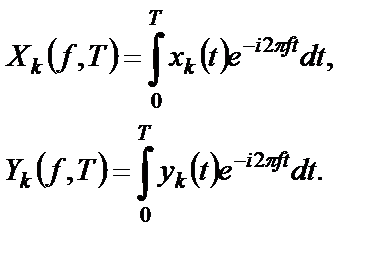
Пусть и – два стационарных эргодических случайных процесса, для которых финитные преобразования Фурье -х реализаций длины определяют в виде

(1.48)

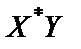
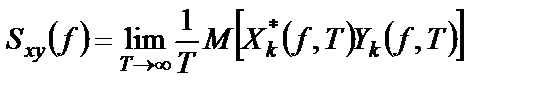
Двусторонняя взаимная спектральная плотность этих случайных процессов вводится с использованием произведения через соотношение

, (1.49)

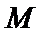
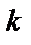
где оператор математического ожидания означает операцию усреднения по индексу .

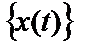
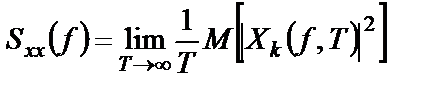
Расчет двусторонней спектральной плотности случайного процесса осуществляют по соотношению

. (1.50)

Аналогично вводятся и односторонние спектральные плотности:

(1.51)

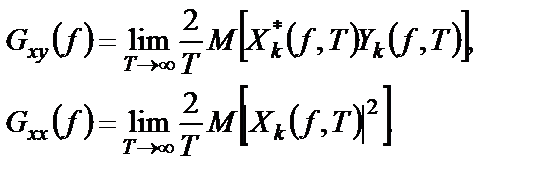
Функции 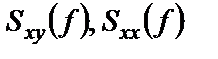, определенные формулами (1.49), (1.50), идентичны соответствующим функциям, определенным соотношениями (1.32), (1.33) как преобразования Фурье над ковариационными функциями. Это утверждение носит называние теоремы Винера-Хинчина.

Контрольные вопросы

1. Приведите классификацию детерминированных процессов.

2. В чем отличие между полигармоническими и почти периодическими процессами?

3. Сформулируйте определение стационарного случайного процесса.

4. Какой способ усреднения характеристик эргодического случайного процесса предпочтителен – усреднение по ансамблю выборочных функций или усреднение по времени наблюдения одной реализации?

5. Сформулируйте определение плотности распределения вероятности случайного процесса.

6. Запишите выражение, связывающее корреляционную и ковариационную функции стационарного случайного процесса.

7. В каком случае два случайных процесса считаются некоррелированными?

8. Укажите способы расчета среднего квадрата стационарного случайного процесса.

9. Каким преобразованием связаны спектральная плотность и ковариационная функции случайного процесса?

10. В каких пределах изменяются значения функции когерентности двух случайных процессов?

Литература

1. Сергиенко, А.Б. Цифровая обработка сигналов / А.Б. Сергиенко. – М: Питер, 2002.– 604 с.

2. Садовский, Г.А. Теоретические основы информационно-измерительной техники / Г.А. Садовский. – М.: Высшая школа, 2008. – 480 с.

3. Бендат, Д. Применение корреляционного и спектрального анализа / Д. Бендат, А. Пирсол. – М.: Мир, 1983. – 312 с.

4. Бендат, Д. Измерение и анализ случайных процессов / Д. Бендат, А. Пирсол. – М.: Мир, 1974. – 464 с.

Источник