Что такое спин электрона

Спин электрона. Часть 1 — Эксперимент Штерна-Герлаха.

Спин (spin – вращение) это наиболее простая вещь на которой можно продемонстрировать отличия квантовой механики от классической. Из определения кажется, что связан он с вращением, но не надо представлять себе электрон или протон вращающимися шариками. Как и в случае многих других устоявшихся научных терминов было доказано что это не так, но терминология уже устоялась. Электрон – точечная частица (нулевого радиуса). А спин отвечает за магнитные свойства. Если электрически заряженная частица движется по кривой траектории (в том числе вращается), то образуется магнитное поле. Электромагниты так работают – электроны движутся по проводам катушки. Но спин отличается от классического магнита. Вот неплохая анимация:

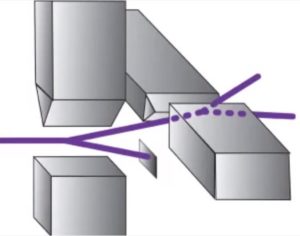
Если магнитики пропускать через неоднородное магнитное поле (обратите внимание на различную форму северного и южного полюсов магнита, задающего поле), то в зависимости от ориентации магнитика (его вектора магнитного момента) они будут притягиваться (отталкиваться) от полюса с большей концентрацией силовых линий магнитного поля (заостренный полюс магнита). В случае перпендикулярной ориентации магнитик вообще никуда не отклонится и попадет в центр экрана.

Пропуская электроны мы будем наблюдать только отклонение вверх или вниз на одно и то же расстояние. Это пример квантования (дискретности). Спин электрона может принимать только одно из двух значений относительно заданной оси ориентации магнита – «вверх» или «вниз». Поскольку электрон мысленно представить себе нельзя (у него нет ни цвета, ни формы, ни даже траектории движения), как и во всех подобных анимациях цветные шарики не отражают реальность, но суть думаю понятна.

Если, например, пропустить вертикально расположенный классический магнитик через два перпендикулярно ориентированных друг относительно друга магнита, то отклоняясь вверх в первом, он не отклонится во втором вообще никак – его вектор магнитного момента будет перпендикулярен линиям магнитного поля. На видео выше это тот случай когда магнитик попадает в центр экрана. Электрон же обязан куда-нибудь отклонится.

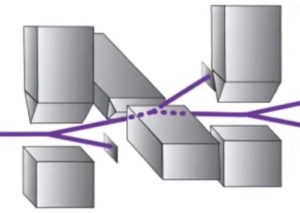
Если мы будем пропускать через второй магнит только электроны со спином вверх, как на рисунке, то окажется что часть из них оказались еще и со спином вверх (вниз) относительно другой перпендикулярной оси. Вправо и влево фактически, но спин измеряют относительно выбранной оси, поэтому «вверх» и «вниз» общепринятая терминология вместе с указанием оси. Вектор не может быть направлен сразу вверх и вправо. Делаем вывод, что спин – это не классический вектор, прикрепленный к электрону наподобие вектора магнитного момента магнитика. Более того, зная, что спин электрона направлен вверх после прохождения первого магнита (отклоняющиеся вниз блокируем), невозможно предсказать куда он отклонится во втором случае: вправо или влево.

Ну и можно еще чуть-чуть усложнить эксперимент – блокировать электроны, отклонившиеся влево и пропустить через третий магнит, ориентированный как и первый.

И мы увидим, что электроны будут отклонятся как вверх, так и вниз. То есть электроны, попадающие во второй магнит все имели спин вверх относительно ориентации первого магнита, а потом часть из них стала вдруг со спином вниз относительно той же самой оси.

Странно! Если через такую конструкцию пропускать классические магнитики, повернутые под одним и тем же произвольно выбранным углом, то они всегда будут попадать в конце в одну и ту же точку экрана. Это называется детерминизмом. Повторив эксперимент при полном соответствии начальных условий мы должны получить тот же результат. В этом заключается основа предсказательной силы науки. Даже наша интуиция основана на повторяемости результатов в схожих ситуациях. В квантовой механике предсказать куда отклонится конкретно взятый электрон в общем случае невозможно. Хотя в некоторых ситуациях есть исключения: если поставить два магнита с одинаковой ориентацией, то если электрон отклонится вверх в первом, то он точно отклонится вверх и во втором. А если магниты повернуты на 180 градусов друг относительно друга и в первом электрон отклонился, например, вниз, то во втором он точно отклонится вверх. И наоборот. Сам по себе спин не меняется. Это уже хорошо)

Какие из всего этого можно сделать общие выводы.

Да, описанные действия с магнитиками называются эксперимент Штерна-Герлаха.

Существует видеоверсия данного поста в части 2 и части 3 элементарного введения в квантовую механику.

Вторая статья цикла про спин электрона: Электроны в магнитном поле.

Источник

Что такое спин электрона

В 1922 году немецкие физики О. Штерн и В. Герлах поставили опыты, целью которых было измерение магнитных моментов P_m атомов различных химических элементов. Для химических элементов, образующих первую группу таблицы Менделеева и имеющих один валентный электрон, магнитный момент атома равен магнитному моменту валентного электрона, т.е. одного электрона.

Идея опыта заключалась в измерении силы, действующей на атом в сильно неоднородном магнитном поле. Неоднородность магнитного поля должна быть такова, чтобы она сказывалась на расстояниях порядка размера атома. Только при этом можно было получить силу, действующую на каждый атом в отдельности.

Схема опыта изображена на рис. 7.9. В колбе с вакуумом, 10 –5 мм рт. ст., нагревался серебряный шарик К, до температуры испарения.

Атомы серебра летели с тепловой скоростью около 100 м/с через щелевые диафрагмы В и, проходя резко неоднородное магнитное поле, попадали на фотопластинку А.

Если бы момент импульса атома (и его магнитный момент ) мог принимать произвольные ориентации в пространстве (т.е. в магнитном поле), то можно было ожидать непрерывного распределения попаданий атомов серебра на фотопластинку с большой плотностью попаданий в середине. Но на опыте были получены совершенно неожиданные результаты: на фотопластинке получились две резкие полосы – все атомы отклонялись в магнитном поле двояким образом, соответствующим лишь двум возможным ориентациям магнитного момента (рис. 7.10).

Этим доказывался квантовый характер магнитных моментов электронов. Количественный анализ показал, что проекция магнитного момента электрона равна магнетону Бора:

.

Таким образом, для атомов серебра Штерн и Герлах получили, что проекция магнитного момента атома (электрона) на направление магнитного поля численно равна магнетону Бора.

.

Опыты Штерна и Герлаха не только подтвердили пространственное квантование моментов импульсов в магнитном поле, но и дали экспериментальное подтверждение тому, что магнитные моменты электронов тоже состоят из некоторого числа «элементарных моментов», т.е. имеют дискретную природу. Единицей измерения магнитных моментов электронов и атомов является магнетон Бора (ħ – единица измерения механического момента импульса).

Кроме того, в этих опытах было обнаружено новое явление. Валентный электрон в основном состоянии атома серебра имеет орбитальное квантовое число l = 0 (s—состояние). Но при l = 0 (проекция момента импульса на направление внешнего поля равна нулю). Возник вопрос, пространственное квантование какого момента импульса обнаружилось в этих опытах и проекция какого магнитного момента равна магнетону Бора.

В 1925 г. студенты Геттингенского университета Гаудсмит и Уленбек предположили существование собственного механического момента импульса у электрона (спина) и, соответственно, собственного магнитного момента электрона Pms.

Введение понятия спина сразу объяснило ряд затруднений, имевшихся к тому времени в квантовой механике. И в первую очередь – результатов опытов Штерна и Герлаха.

Авторы дали такое толкование спина: электрон – вращающийся волчок. Но тогда следует, что «поверхность» волчка (электрона) должна вращаться с линейной скоростью, равной 300 с, где с – скорость света. От такого толкования спина пришлось отказаться.

В современном представлении – спин, как заряд и масса, есть свойство электрона.

П. Дирак впоследствии показал, что существование спина вытекает из решения релятивистского волнового уравнения Шредингера.

Из общих выводов квантовой механики следует, что спин должен быть квантован: , где s – спиновое квантовое число.

Аналогично, проекция спина на ось z (L_sz) (ось z совпадает с направлением внешнего магнитного поля) должна быть квантована и вектор может иметь (2s + 1) различных ориентаций в магнитном поле.

Из опытов Штерна и Герлаха следует, что таких ориентаций всего две: , а значит s = 1/2, т.е. спиновое квантовое число имеет только одно значение.

Для атомов первой группы, валентный электрон которых находится в s—состоянии (l = 0), момент импульса атома равен спину валентного электрона. Поэтому обнаруженное для таких атомов пространственное квантование момента импульса в магнитном поле является доказательством наличия у спина лишь двух ориентаций во внешнем поле. (Опыты с электронами в p—состоянии подтвердили этот вывод, хотя картина получилась более сложной) (желтая линия натрия – дуплет из-за наличия спина).

Численное значение спина электрона:

.

По аналогии с пространственным квантованием орбитального момента проекция спина квантуется (аналогично, как , то и ). Проекция спина на направление внешнего магнитного поля, являясь квантовой величиной, определяется выражением:

,

где – магнитное спиновое квантовое число, , т.е. может принимать только два значения, что и наблюдается в опыте Штерна и Герлаха.

Итак, проекция спинового механического момента импульса на направление внешнего магнитного поля может принимать два значения:

Так как мы всегда имеем дело с проекциями, то говоря, что спин имеет две ориентации, имеем в виду две проекции.

Проекция спинового магнитного момента электрона на направление внешнего магнитного поля:

.

Отношение – спиновое гиромагнитное отношение.

Источник

Спин электрона — определение, классификация и примеры значений

Спин электрона (от англ. «вращение») относится к физическому свойству субатомных частиц, в соответствии с которым каждая элементарная частица имеет собственный момент импульса фиксированной величины.

Это внутреннее свойство, такое как масса или электрический заряд. Когда говорят о спине, вместо буквы l пишется буква s.

В 1920 году химики пришли к выводу, что с известными квантовыми числами (масса, электрический заряд) было невозможно полностью описать электроны в атоме. В химии электроны играют ведущую роль.

Что такое спин в физике

Около 1925 г. три исследователя Ральф Крониг, Гаудсмит и Уленбек начали с идеи, что электрон, который вращается вокруг атомного ядра, похож на Землю, двигающуюся вокруг Солнца.

Как Земля имеет вращательное движение, так и электрон, связанный с атомом, вращается сам по себе.

Полный угловой момент Земли представляет собой векторную сумму ее орбитального углового момента и ее углового момента вращения. Но в случае электрона нельзя рассчитать его угловой момент вращения так, как рассчитывают момент Земли, основываясь на массе, радиусе и угловой скорости.

Электрон является держателем отрицательного электрического заряда. Вращение создает магнитное поле, которое называется спином.

Спин обеспечивает меру собственного момента импульса каждой частицы. Он необходим, чтобы определить тип частицы.

Добавив спин в качестве четвертого числа, можно было дать более полное объяснение характеристик спектров атомов, обладающих одним электроном. Можно представить электрон как крутящийся мяч, а спин как связанный с этим вращением момент. Но в этом случае скорость движения получится выше скорости света.

Существование спина подтверждается многими экспериментальными результатами. До сих пор неизвестно, из чего складывается спин протона. Нельзя провести измерение относительно оси Х и оси У одновременно.

Вскоре концепция была распространена на все субатомные частицы, включая протоны, нейтроны и античастицы. Свойства большинства парамагнитных и ферромагнитных веществ определяет обусловленный спином электрона магнитный момент.

Техника и наука нашли широкое применение определенных свойств, связанных с этим физическим свойством. Правило Хунда говорит, что суммарный спин должен быть максимальным (при распределении электронов в пределах энергетического уровня).

Классификация элементарных частиц по спину

Какое значение может принимать спиновое квантовое число?

Принципы квантовой механики указывают, что значения спина в нормальных условиях ограничены целым или полуцелым числом, кратным постоянной Планка.

Фермионы (электроны, кварки, нейтрино) имеют полуцелые значения (½, 3/2).

Бозоны (фотоны, глюоны, бозоны) имеют спины 0, 1, 2. У фотона спин — 1.

Некоторые экзотические частицы, такие как пион, имеют значение 0.

1/2 — это спин одиночного электрона. Такая система называется дублет.

Магнитный спиновый момент существует для незаряженных частиц, таких как фотон. Ферромагнетизм возникает из-за выравнивания спинов (иногда и от орбитальных магнитных моментов).

В настоящее время микроэлектроника находит применение для определенных свойств или эффектов, связанных с природой вращения, таких как магнитосопротивление или гигантское магнитосопротивление, которое используется в жестких дисках.

Также рассматривается возможность использования этих свойств для будущих компьютеров, в которых спин изолированной системы может служить квантовым битом (кубитом). Сейчас ученые пытаются контролировать спин, используя сверхкороткие импульсы лазера.

Квантовое число характеризует собственный момент движения электрона, одно из состояний микрофизической системы (например, атома, молекулы и т. д.), возможных согласно квантовой теории. Обычно это целое или полуцелое число (n или n + 1/2).

Для четкого описания системы необходимо предоставить полный набор чисел (измеренных одновременно). Открытие трудно переоценить. Без него нельзя было бы построить квантовые вычислители, а многие свойства атомов и материалов так и остались бы загадкой.

Источник