Что такое сплайн в векторной графики

Использование сплайнов в графических средах

Как показала практика, сплайны оказались очень удобным инструментом при построении различных графических изображений.

Сплайн является важным объектом векторной графики, с его помощью можно описывать ту или иную геометрическую фигуру. Например, с использованием сплайнов построены современные шрифты TrueType и PostScript.

У векторной графики много достоинств. Она экономна в плане дискового пространства, необходимого для хранения изображений: это связано с тем, что сохраняется не само изображение, а только некоторые основные данные, используя которые, программа всякий раз воссоздает изображение заново. Кроме того, описание цветовых характеристик почти не увеличивает размер файла.

Объекты векторной графики легко трансформируются и модифицируются, что не оказывает практически никакого влияния на качество изображения. Масштабирование, поворот, искривление могут быть сведены к нескольким элементарным преобразованиям над векторами.
В тех областях графики, где важное значение имеет сохранение ясных и четких контуров (например, в шрифтовых композициях, в создании логотипов и прочее), векторные программы незаменимы.

Для работы со сплайнами в векторной графике используется множество программных пакетов (ArchiCAD, 3ds max, Maya).

В дипломной работе изучается как используются сплайны в графических средах и математических процессорах 3ds Max и Maple.

Источник

Сплайны (Spline — кусочно-полиномиальная функция) — это двумерные геометрические объекты, которые совершенно самостоятельны и могут служить основой для построения более сложных трехмерных тел. Внешне сплайны представляют собой разнообразные линии, форма линии определяется типом вершин, через которые она проходит. Сплайнами могут быть как простейшие геометрические фигуры: прямоугольники, звезды, эллипсы и пр., так и сложные ломаные или кривые, а также контуры текстовых символов.

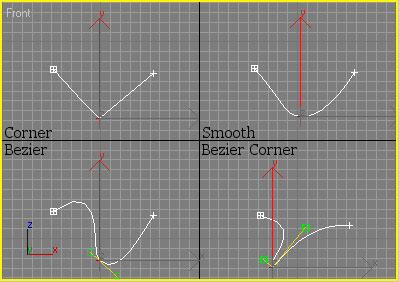
Основными элементами сплайнов являются вершины (Vertex) и сегменты (Segment). Вершинами называют точки, расположенные на сплайне, при этом первая вершина, обозначающая начало сплайна, отмечается квадратиком белого цвета. Под сегментом принято понимать участок линии сплайна, ограниченный двумя соседними вершинами, — сегменты могут быть как прямо-, так и криволинейными отрезками. Вершины сплайна различаются по типу, от которого зависит степень кривизны прилегающих к данным вершинам сегментов сплайна. Всего выделяют четыре типы вершин (рис. 1):
Corner (Угловая) — вершина, в которой сплайн имеет излом, а примыкающие к ней сегменты лишены кривизны.
Smooth (Сглаженная) — вершина, через которую кривая сплайна проводится с плавным изгибом, а кривизна прилегающих к вершине сегментов одинакова с обеих сторон.
Bezier (Безье) — вершина, напоминающая сглаженную и отличающаяся от нее возможностью управления степенью кривизны обоих сегментов. Последнее осуществляется благодаря наличию в вершине касательных векторов, ограниченных на концах маркерами в виде квадратиков зеленого цвета и называемых ручками Безье. Перемещая ручки Безье, можно изменять направление, в соответствии с которым сегменты сплайна входят в вершину и выходят из нее, а изменяя расстояние от маркеров до вершины — регулировать степень кривизны сегментов сплайна. У вершин данного типа ручки Безье связаны между собой, и перемещение одной из них автоматически вызывает перемещение второй.
Bezier Corner (Безье угловая) — вершина, имеющая касательные векторы, позволяющие управлять степенью кривизны сегментов, однако, в отличие от вершин Bezier, у вершин Bezier Corner касательные векторы не связаны друг с другом и перемещение одного из маркеров не зависит от перемещения другого.

Сегменты также различаются по типу: Curve (Кривая) или Line (Линия). Выбрав типа Curve, можно получить криволинейные сегменты, если вершины являются гладкими или имеют тип Безье, в случае же угловых вершин даже при установке типа Curve сегмент останется линейным. Выбор типа Line приводит к игнорированию типа вершин, в результате чего сегмент данного типа всегда выглядит линейным.

Источник

Сплайн

Сплайны имеют многочисленные применения как в математической теории, так и в разнообразных вычислительных приложениях. В частности, сплайны двух переменных интенсивно используются для задания поверхностей в различных системах компьютерного моделирования.

Содержание

Определение и история

Теория интерполяции сплайнами и сам термин сплайн ведут свой отсчёт со статьи Айзека Шонберга (англ. Isaac Jacob Schoenberg ) 1946 года. Особенно интенсивное её развитие произошло в 50-70 годы, традиционной прикладной сферой использования интерполяционных сплайнов стали в настоящее время системы автоматизированного проектирования. Однако потенциальные возможности сплайнов значительно шире, чем просто описание некоторых кривых. В реальном мире большое количество физических процессов по самой своей природе являются сплайнами. В механике это деформация гибкой пластины или стержня, зафиксированных в отдельных точках; траектория движения тела, если сила, действующая на него меняется ступенчато (траектория искусственного космического объекта с активными и инерционными отрезками движения, траектория движения самолета при ступенчатой ​​изменении тяги двигателей и изменении профиля крыла и т. д.). В термодинамике это теплообмен в стержне, составленном из фрагментов с различной теплопередачей. В химии — диффузия через слои различных веществ. В электричестве — распространение электромагнитных полей через разнородные среды. То есть, сплайн не надуманная математическая абстракция, а во многих случаях он является решением дифференциальных уравнений, описывающих вполне реальные физические процессы.

Рассмотрение сплайнов начнем с определения алгебраического сплайна []: Функция определенная и непрерывная на отрезке , называется полиномиальным сплайном порядка с узлами , если на каждом из отрезков , является алгебраическим полиномом степени, не превышающей , а в каждой из точек некоторая производная может иметь разрыв. Если в точке непрерывные функции , а производная в точке терпит разрыв, число называют дефектом сплайна. Множество называют сеткой узлов сплайна, а точки узлами или точками соприкосновения или склейки сплайна.

Как следует из определения, для построения сплайна, состоящего из фрагментов, требуется найти такие значения числовых параметров для каждого фрагмента — полинома степени , которые обеспечат непрерывность в узлах как самой функции, так и необходимых производных. Так, всего следует определить параметров. С учетом условия интерполяции и непрерывности первых двух производных определение параметров сводится к решению системы с линейных уравнений. Как правило, значения коэффициентов для отрезков полиномов непосредственно не рассчитываются.

Для определения интерполяционного сплайна с непрерывной первой производной, достаточно рассчитать значение первой производной в узлах. Способ определения производных в узлах сплайна определяет широкое разнообразие интерполяционных сплайнов. Часто производные определяются не как константы, а как некоторые зависимости от интерполируемой функции и сетки интерполяции.

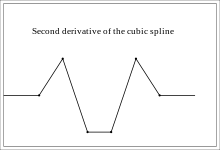
Если значение первой производной в узлах рассчитывать исходя из условия непрерывности второй производной (решая систему с n линейных уравнений), то сплайн будет иметь две непрерывные производные. Такой способ построения сплайна, как и сам сплайн называют глобальным, поскольку при определении каждого из его коэффициентов учитывается все множество узлов интерполяции.

В других случаях, для определения отдельного коэффициента учитываются только ближайшие узлы интерполяции и такие способы построения, как и сами сплайны, называют локальными. Параметры фрагмента такого сплайна можно определить независимо от других фрагментов.

Простым условием построения фрагмента локального сплайна является условие равенства полинома на концах отрезков соответствующим значениям интерполируемой функции.

Для простейшего сплайна — ломаной — этого условия вполне достаточно. Два коэффициента прямой однозначно определяются из двух уравнений. Такой сплайн является локальным. Для полиномов высших степеней мы должны добавить дополнительные условия таким образом, чтобы общее число уравнений было равно числу коэффициентов полинома. Так, для сплайна 3-й степени таким условием является равенство 1-й производной на концах отрезка некоторому значению, которое определяется для соседних участков одинаковым образом (в формулах (2) через значение производной функции, которой приближают).

Система из 4-х уравнений

позволяет однозначно определить 4 коэффициента полинома. Для полинома 5-й степени мы должны дополнительно наложить условие равенства 2-й производной на концах отрезка и т. д. Приведенное выше показывает, почему сплайны строят преимущественно из полиномов нечётных степеней (с чётным количеством коэффициентов).

Для полиномов четных степеней при сборке системы (3) остается неопределенной производная в одном из концов отрезка, и условие равенства производных (гладкости кривой) не будет выполняться. Поэтому для полинома 2-й степени невозможно достичь равенства первой производной в точках стыка, а для 4-й степени — второй производной и т. д., исходя из системы уравнений (3). Для построения сплайнов с четными степенями искусственно добавляют дополнительные условия чтобы сформировать систему уравнений, подобную (3). Когда производные полинома сплайна определяются как соответствующие производные интерполируемой функции, то сплайн является эрмитовым.

Существуют локальные методы построения сплайнов Бесселя и Акими, B — сплайны []. В основном, когда речь идет о сплайнах, то имеют в виду сплайны, построенные из алгебраических полиномов. Именно к ним относится приведенное выше определение. Именно эти сплайны являются наиболее изученными. Однако сплайн может состоять из фрагментов функций любого класса. В [] рассмотрено построение таких сплайнов и исследуются их свойства. Автор не дает общего определения построенных сплайнов. Очевидно, что для любых классов функций, из которых состоит сплайн, приведенное в начале статьи определение не совсем подходит. Если, например, сплайн состоит из отрезков экспоненты, то понятие дефекта сплайна теряет смысл. Хотя количество непрерывных производных останется важной характеристикой. Построение сплайна, фрагментами которого являются разрывные функции (рациональные функции, функции Паде), несколько выходит за рамки сплайновой идеи, поскольку одним из основных преимуществ сплайнов является их гладкость. Если произвольно расширять такие конструкции, то стираются различия сплайнов от кусковых функций. Другим преимуществом сплайнов является эффективность вычислений. Чрезмерное усложнение фрагментов существенно снижает преимущество сплайнов перед классическими функциями.

Классификация сплайнов

Как отмечалось выше, существует большое количество конструкций, которые называют сплайнами. Поэтому необходимо внести определенную классификацию в это многообразие, имея целью выделить те признаки, которые позволят выбрать сплайны годные для конкретной прикладной задачи.

Вид фрагментов сплайна. То, что сплайн состоит из фрагментов одинакового вида, является одним из ключевых признаков, что отличает его от других кусковых функций.

Самые известные сплайны — состоящие из фрагментов — алгебраических полиномов не выше заданной степени. Как правило, это кубические полиномы, или полиномы нечётных степеней: первой, третьей (кубический), пятой степени. Более высокие степени применяют редко из-за усложнения расчетов и сложностей, описанных в предыдущем разделе. Основным их преимуществом является простота расчетов и анализа. Недостатком является то, что относительно мало реальных физических процессов соответствуют этой зависимости.

Экспоненциальные сплайны. Если гибкую металлическую линейку, зафиксированную в узлах, натянуть, то решением дифференциального уравнения будет не алгебраический полином, а экспонента. Поэтому такие сплайны называют также напряженными. Экспонента описывает многие физические процессы в динамических системах. Недостатком является трудоёмкость расчета.

Тригонометрическими являются сплайны, фрагменты которых описываются тригонометрическими полиномами. Имеют достаточно сложные расчетные выражения. Более пятидесяти различных по виду фрагментов сплайнов описаны в работах Б. А. Попова.

Также существуют рациональные сплайны и сплайны Паде. Их особенностью является возможность разрыва производных на фрагментах, при непрерывности в узлах. М. Ансерме строит фракциональные сплайны, где фрагменты заданы с помощью гамма-функции.

Целесообразность применения фрагментов определенного вида основана на конкретных условиях задачи и ограничениях реализации. Как правило, основное требование — это достижение заданной точности интерполяции при приемлемых затратах времени и ресурсов на реализацию. Удачный выбор фрагментов, который соответствует характеру процесса, позволяет сократить время вычислений и требуемый объём памяти.

Число фрагментов. Очевидно, что минимальное число фрагментов — один. Классическое определение сплайна ограничивает число фрагментов определенным числом на конечном отрезке. Однако можно строить сплайны и с бесконечным числом фрагментов, а реально эти методы и алгоритмы, которые не нуждаются в информации об определенном количестве фрагментов. Представителями этих сплайнов являются кардинальные сплайны, исследованные Шенбергом. Для построения сплайнов с неограниченным числом фрагментов лучше подходят локальные сплайны.

Ширина фрагментов. Следует выделить сплайны с равной шириной фрагментов. Это позволяет значительно упростить расчетные выражения, ускорить работу алгоритмов и снизить затраты на реализацию. Определенного упрощения можно достичь за счёт применения фрагментов с кратной шириной. Существуют сплайны с нулевой шириной фрагментов (Де Бур). Это приводит к кратности узлов и возможности приближать сплайны с неразрывными фрагментами разрывных функций. Расчетные выражения получают в результате предельных переходов. Сплайны могут иметь также фрагменты с бесконечной шириной. Эти фрагменты должны быть крайними. Иногда это позволяет естественно задать краевые условия.

Условия стыковки фрагментов. Еще один важный признак, что отличает сплайны. Когда идет речь о сплайнах, как правило, считают, что фрагменты стыкуются гладко. То есть обеспечивается непрерывность значений и первой производной. Понятие дефекта сплайна связано с числом непрерывных производных, которые имеет функция-фрагмент определенного вида и числом производных, непрерывность которых гарантирована в узлах. Экспонента, синусоида имеют бесконечное число производных. Для них это понятие не имеет смысла. Поэтому удобнее говорить прямо о числе производных, непрерывность которых гарантирована в узлах сплайна. Практически речь идет о непрерывности значений и первой, максимум второй производной. Разрыв второй и высших производных визуально не заметно, поэтому учитывается редко. Понятно, что первая производная в точках стыка может задаваться по-разному. Наиболее распространены два приёма. Значение первой производной выбирается так, чтобы обеспечить непрерывность второй (глобальные кубические сплайны минимального дефекта). Первая производная равняется первой производной интерполируемой функции (возможно приближенно) в эрмитовых сплайнах.

Краевые условия. Если сплайны имеют ограниченное число фрагментов, то, естественно, у них отсутствуют крайние фрагменты слева и справа, поэтому крайние узлы не с чем стыковать. Исключением являются лишь периодические сплайны, которые имеют естественное продолжение. Иногда естественными называют краевые условия с нулевой производной, хотя никаких оснований считать их более естественными, чем другие, нет. Если сплайн имеет фрагменты одинаковой ширины, считают недостающие фрагменты той же ширины. Другой вариант — это считать недостающие фрагменты продлёнными в бесконечность. Преимущество такого подхода в возможности экстраполяции. Можно считать ширину фрагментов нулевой. Расчетные выражения получают предельными переходами. Если взглянуть на краевые условия с точки зрения формирования сплайна из базисных функций, то они сводятся к продолжению соответствующих локальных базисных функций. Ширина соседних фрагментов влияет на их форму. А простое обрезание часто приводит к осцилляции и росту погрешности на краях. Важное значение краевые условия имеют при обработке изображений и в задачах с экстраполяцией.

Дополнительные ограничения. Они чаще всего касаются производных в узлах. Иногда они вытекают из физики процесса. Условия: неотъемлемость значений, равенство моментов, площадей, условия нормирования. Дополнительные условия иногда упрощают анализ свойств сплайнов, но могут серьезно затруднять построение и затраты реализации.

Сетка точек интерполяции. Может существенно влиять на эффективность расчетов. Важны случаи равномерной сетки и равномерной сетки, с расстоянием между точками, кратным расстоянию между узлами сплайна.

Локальные свойства базисных функций. Сплайн можно представить как сумму взвешенных базисных сплайнов. Существенным является ширина этих базисных функций. Так, в глобальных сплайнах базисные сплайны ненулевые на всём отрезке интерполяции. Хотя стоит заметить, что с определенной точностью (достаточной для многих технических расчетов) их можно считать локальными. У локальных сплайнов ширина базисных функций невелика (четыре фрагмента у кубических эрмитовых сплайнов). Это существенно влияет на эффективность расчетов и затраты реализации.

Форма представления. Функции, задающие фрагменты сплайна, как правило, зависят от множества параметров, благодаря которым они меняют свою форму. Значения параметров на каждом из фрагментов индивидуальны. Эти параметры могут задавать конкретный сплайн. Для полиномиальных сплайнов это полиномиальные коэффициенты. Так, сплайн можно представить множеством параметров функций на каждом из фрагментов. Назовем это представление пофрагментным. Такое представление является наглядным, часто имеет явный физический смысл. Но число параметров является чрезмерным. Так, для кубического сплайна необходимо иметь 4 * (r-1) параметров (r — число узлов сплайна). Значительно более компактным является представление сплайна в виде полинома, через базисные сплайн-функции в виде:

,

где — базисные сплайн-функции (как правило локальные), — числовые коэффициенты, задающие вес базисных функций при формировании сплайна. Число параметров, задающих сплайн, равно числу узлов сплайна. Между параметрами функции на фрагменте и коэффициентами полинома-сплайна существует зависимость, что позволяет с одними коэффициентами находить другие, хотя формулы могут иметь достаточно сложный вид.

Содержание коэффициентов сплайна. Как отмечалось в предыдущем пункте, содержание параметров сплайна при пофрагментном представлении определяется типом функции. При полиномиальном представлении следует выделить случай, когда коэффициенты имеют тот же физический смысл, что и входные данные. То есть, коэффициенты являются значениями сплайна в узлах. Такую форму называют Лагранжевой, по аналогии с полиномом Лагранжа. Следует заметить, что базисные сплайны этой формы равны единице в центральном узле и нулю во всех остальных.

Особые сплайны. В ряде случаев рассматривают функции, которые находятся близко к границе между сплайнами и обычными функциями, а также сплайнами и кусковыми функциями. К примеру, это сплайны, состоящие из двух фрагментов. Имеют упрощенный вариант построения, но особое внимание следует уделять краевым условиям.

Источник

Сплайны в 3d графике, максимально автоматизированный вариант

С месяц назад начал учить Python по книге Доусона и очнулся уже глубоко в процессе написания своей игры под pygame. ТЗ было таково, что наиболее перспективным показалось сделать игру с псевдо-трехмерной графикой, запихнув в спрайты сохраненные поверхности 3d-сплайнов. О последних и напишу.

Итак, имеются полигоны (проще всего работать с четырехугольниками), на которые мы хотим натянуть кубические поверхности так, чтобы они стыковались достаточно плавно — эти поверхности и есть сплайны.

Удобнее всего сплайн для одного полигона представить в виде функции

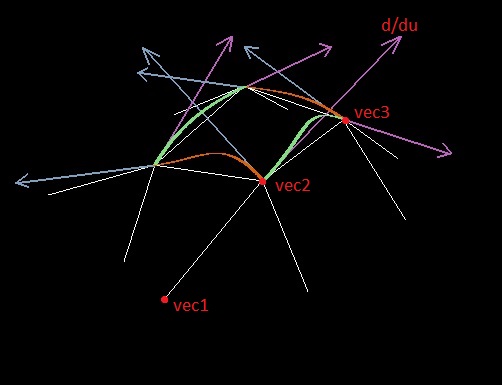
— кубические многочлены, удовлетворяющие каким-то граничным условиям (на рисунке ниже — салатовые и рыжие кривые, а производные-начальные условия — сиреневые и голубые вектора); u и v меняются в пределах от 0 до 1.

В такой интерпретации теряются некоторые степени (произведения 2-х и 3-х степеней параметров), зато коэффициенты многочлена можно найти, задав всего 12 векторов начальных условий (4 точки полигона и вектора производных по u и по v для каждой точки). На стыках сплайны совпадают, если задаются аналогичные начальные условия для соседних полигонов (вектора производных должны быть коллинеарны, поверхность проходит через те же точки полигона).

Одна беда — производная при такой постановке задачи на всей границе может не совпадать — будут небольшие артефакты на стыках. Можно выдумать еще 4 условия для исправления этого и аккуратно добавить в формулу еще один член

который не испортит границы, но это тема для отдельной статьи.

Альтернативный вариант — Поверхность Безье, но в нем предлагается задавать 16 параметров непонятного (мне) математического смысла, т.е. предполагается, что будет работать своими руками художник. Мне это не очень подходит, поэтому далее следует велосипед с костылями.

Коэффициенты (1) проще всего вычислить, найдя обратную матрицу к матрице значений и производных в углах и помножив на входные условия (три раза, для каждой координаты). Матрица может быть такой:

NumPy отлично с этой задачей справляется.

Остался один вопрос — откуда взять векторы производных. Предполагается, что надо их как-то выбирать исходя из положения соседних (для полигона) точек и из соображения гладкости.
Лично для меня еще было совершенно контринтуитивно, как быть с длиной вектора производной. Направление — понятно, а вот длина?

В итоге родился такой алгоритм:

1. На первом этапе происходит некоторая классификация точек. В графе (который задают точки полигонов и их связи) ищутся и запоминаются циклы длиной 4, а кроме того записываются соседи, наиболее подходящие на роль продолжения ребра полигона (заранее определяется, какие ребра соответствуют изменению параметра u, а какие — v). Вот кусок кода, который ищет, сортирует и запоминает соседей для 0-й точки какого-то цикла:

Дальше, при построении сплайна, производная вдоль ребра (например по параметру u) в точке полигона выбирается исходя из расположения двух точек ребра и одной соседней точки (пусть это будут точки vec1, vec2 и vec3; точка в которой ищется производная — вторая).

Сначала я пытался использовать для этой роли нормированный вектор vec3 — vec1 (типа применил теорему Лагранжа), но проблемы возникли именно с длиной вектора производных — делать его константой было плохой идеей.

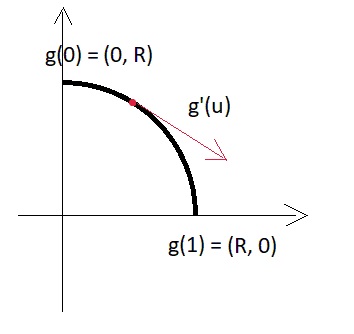
Для небольшой иллюстрации, что такое вектор производной в параметрическом варианте, обратимся к простой двумерной аналогии — вот кусок дуги окружности:

Т.е. модуль производной = R*pi/2 и, вообще говоря, зависит от размера куска дуги, который мы задали через параметр.

Что же с этим теперь делать? Лев Николаевич Толстой завещал нам, что все круглое = хорошее, поэтому, если мы зададим производную в точке так, как если бы хотели построить там дугу, — у нас получится гладкая красивая кривая.

Конец лирического отступления.

Второй этап поиска производной:

2. Через наши три точки vec1, vec2, vec3 строим плоскость, в этой плоскости ищем окружность, которая проходит через все три точки. Искомая производная будет направлена по касательной к окружности в точке vec2, а модуль вектора производной должен равняться произведению радиуса окружности и угла сектора, который образуют две точки грани полигона (аналогично нашей простой плоской аналогии из лирического отступления).

Вроде все просто, вот код функции, например (опять используется NumPy):

Ну и в общем, это все как-то работает. Для демонстрации я взял куб 5х5х5 и менял положение точек рандомайзером:

Источник