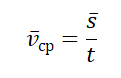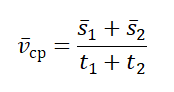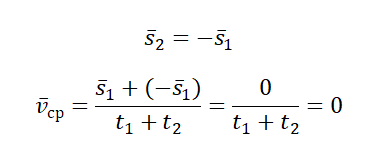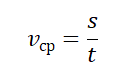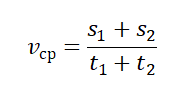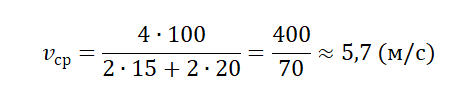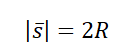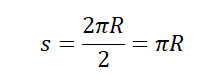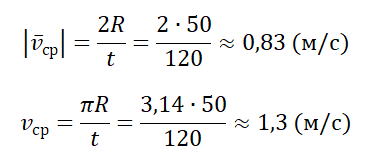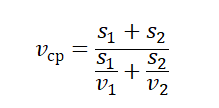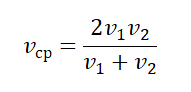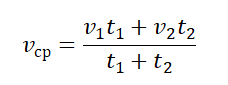Что такое средняя скорость неравномерного движения
I. Механика
Тестирование онлайн
Виды неравномерного движения
Неравномерным считается движение с изменяющейся скоростью. Скорость может изменяться по направлению. Можно заключить, что любое движение НЕ по прямой траектории является неравномерным. Например, движение тела по окружности, движение тела брошенного вдаль и др.
Иногда встречается неравномерное движение, которое состоит из чередования различного вида движений, например, сначала автобус разгоняется (движение равноускоренное), потом какое-то время движется равномерно, а потом останавливается.
Мгновенная скорость
Охарактеризовать неравномерное движение можно лишь скоростью. Но скорость всегда изменяется! Поэтому можно говорить лишь о скорости в данное мгновение времени. Путешествуя на машине спидометр ежесекундно демонстрирует вам мгновенную скорость движения. Но время при этом надо уменьшить не до секунды, а рассматривать гораздо меньший промежуток времени!
Средняя скорость

У средних величин рисуют сверху горизонтальную черту.
Средняя скорость перемещения. Средняя путевая скорость
Главное запомнить
1) Определение и виды неравномерного движения;
2) Различие средней и мгновенной скоростей;
3) Правило нахождения средней скорости движения
Формула для определения средней скорости*
Часто требуется решить задачу, где весь путь разбит на равные участки, даны средние скорости на каждом участке, требуется найти среднюю скорость движения на всем пути. Неверное решение будет, если сложить средние скорости и разделить на их количество. Ниже выводится формула, которую можно использовать при решении подобных задач.
Определение мгновенной скорости графически*
Упражнения
Во время езды на автомобиле через каждую минуту снимались показания спидометра. Можно ли по этим данным определить среднюю скорость движения автомобиля?
Нельзя, так как в общем случае величина средней скорости не равна среднему арифметическому значению величин мгновенных скоростей. А путь и время не даны.
Какую скорость переменного движения показывает спидометр автомобиля?
Близкую к мгновенной. Близкую, так как промежуток времени должен быть бесконечно мал, а при снятии показаний со спидометра так о времени судить нельзя.
В каком случае мгновенная и средняя скорости равны между собой? Почему?
При равномерном движении. Потому что скорость не изменяется.
Скорость движения молотка при ударе равна 8м/с. Какая это скорость: средняя или мгновенная?
Поезд прошел путь между городами со скоростью 50км/ч. Какая это скорость: средняя или мгновенная?
*Два шарика начали одновременно и с одинаковой скоростью двигаться по поверхностям, имеющим форму, изображенную на рисунке. Как будут отличаться скорости и время движения шариков к моменту их прибытия в точку В? Силу трения не учитывать.
Задача решается графическим способом. Скорости будут одинаковы. Время движения второго шарика меньше. Примерные графики движения шариков приведены на рисунке. Так как пути. пройденные шариками, равны, то, как видно из графика (на графике пути численно равны площадям заштрихованных фигур), время второго шарика меньше времени первого.
Неравномерное движение и средняя скорость
теория по физике 🧲 кинематика
Неравномерное движение — движение с переменной скоростью, которая может менять как направление, так и модуль.
Неравномерное движение можно охарактеризовать средней скоростью. Различают среднюю векторную и среднюю скалярную скорости.
Средняя векторная скорость
Средняя векторная скорость — это скорость, равная отношению перемещения тела ко времени, в течение которого это перемещение было совершено.
v ср — средняя векторная скорость, s — перемещение тела, совершенное за время t
Направление вектора средней скорости всегда совпадает с направлением вектора перемещения.
Чтобы вычислить среднюю векторную скорость, нужно поделить сумму всех перемещений на сумму всех временных промежутков, в течение которых эти перемещения были совершены:
Пример №1. Миша пробежал стометровку за 16 секунд. Через 1 минуту он вернулся на старт. Найти среднюю векторную скорость мальчика.
Миша совершил одинаковые по модулю, но разные по направлению перемещения. При сложении этих векторов получается 0. Поэтому средняя векторная скорость также равна нулю:
Средняя скалярная скорость
Средняя скалярная (путевая) скорость — это скорость, равная отношению пути, пройденного телом, ко времени, в течение которого этот путь был пройден.
vср — средняя путевая скорость, s — путь, пройденный телом за время t
Чтобы вычислить среднюю путевую скорость, нужно поделить сумму всех путей на сумму всех временных промежутков, в течение которых эти пути были преодолены:
Пример №2. Мальчик пробежал по периметру квадратного поля сто стороной 100 м. На первые две стороны мальчик потратил по 15 секунд, а на последние две — по 20 секунд. Найти среднюю путевую скорость мальчика.
У квадрата 4 стороны, поэтому путь мальчика составляют 4 дистанции по 100 м каждая. Поэтому средняя путевая скорость равна:
Средняя скалярная скорость всегда больше или равна модулю средней векторной скорости:
Пример №3. Рыболов остановился на берегу круглого пруда и увидел на противоположном берегу удобное для рыбалки место. Он к нему шел в течение 2 минут. Вычислите среднюю путевую и среднюю векторную скорости рыболова после того, как он придет на новое место, если радиус пруда равен 50 м.
Две противоположные точки окружности соединяются отрезком, проходящим через его центр — диаметром. Поэтому модуль вектора перемещения равен двум радиусам пруда:
Чтобы дойти до диаметрально противоположной точки окружности, нужно пройти путь, равный половине окружности:
Переведя 2 минуты в СИ, получим 120 с. Модуль средней векторно скорости равен:
Пример №4. Первые полчаса автомобиль двигался со скоростью 90 км/ч, а потом 1 час он двигался со скоростью 60 км/ч. Найти среднюю скорость автомобиля.
Нам известны скорости на каждом из участков пути и время, в течение которого каждый из этих участков был преодолен. Поэтому:
Что такое средняя скорость неравномерного движения
Неравномерное движение — это движение, при котором за равные промежутки времени тело проходит разные пути.
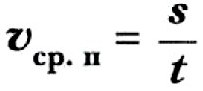
Средняя путевая скорость — скалярная неотрицательная величина.
Средняя скорость тела за промежуток времени t — это физическая величина, равная отношению перемещения 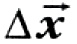
Средняя скорость — вектор. Она направлена туда, куда направлено перемещение тела за рассматриваемый промежуток времени.
Если тело всё время движется в одном направлении, то модуль средней скорости равен средней путевой скорости. Если же в процессе своего движения тело меняет направление движения, то модуль средней скорости меньше средней путевой скорости.
Пример решения задач на среднюю скорость при неравномерном движении
Автомобиль проехал за первый час 50 км, а за следующие два часа он проехал 160 км. Какова его средняя скорость за все время движения?
Еще больше задач на движение (с решениями и ответами) в конспекте «Задачи на движение»
Это конспект по физике за 7 класс по теме «Неравномерное движение. Средняя скорость». Выберите дальнейшие действия:
Неравномерное прямолинейное движение. Средняя скорость
п.1. График скорости при неравномерном прямолинейном движении
Прямолинейное и равномерное движение возможно лишь на участке пути.
Любое тело со временем меняет свою скорость, как по величине, так и по направлению.
Для описания неравномерного движения его можно разбить на участки, на которых скорость постоянна, и свести задачу к уже известному нам равномерному прямолинейному движению.
п.2. Как найти путь и перемещение по графику скорости?
Мы уже знаем, что путь равен площади прямоугольника, который образуется между отрезком графика скорости и отрезком \(\triangle t\) на оси \(t\) (см. §8 данного справочника).
п.3. Средняя скорость и средняя путевая скорость
В нашем примере с велосипедистом, который все время двигался в одну сторону и дошел до города B, получаем: \begin
А вот для случая, когда велосипедист развернулся и пошел обратно: \begin
п.4. Задачи
Задача 1. По графику скоростей найдите среднюю скорость и среднюю путевую скорость движения.
Задача 2. Мотоциклист проехал расстояние между двумя пунктами со скоростью 40 км/ч. Потом увеличил скорость до 80 км/ч и проехал расстояние в два раза меньше. Найдите среднюю скорость мотоциклиста за все время движения.
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | 40 | \(\frac<2d><40>=\frac | \(2d\) |
| 2й участок | 80 | \(\frac | \(d\) |
| Сумма | — | \(t=\frac | \(s=2d+d=3d\) |
Задача 3. Автомобиль проехал первую половину пути по шоссе со скоростью 90 км/ч, а вторую половину – по грунтовой дороге со скоростью 30 км/ч. Найдите среднюю скорость автомобиля.
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | 90 | \(\frac | \(\frac s2\) |
| 2й участок | 30 | \(\frac | \(\frac s2\) |
| Сумма | — | \(t=\frac | \(s\) |
Задача 4*. Туристы прошли по маршруту со средней скоростью 32 км/ч. Маршрут был разделен на три участка, первый участок преодолевался пешком, второй – на автобусе, третий – на катере. Найдите скорость на каждом участке, если длины этих участков относятся как 1:4:45, а соответствующие интервалы времени как 4:1:20.
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | \(\frac | \(4t\) | \(d\) |
| 2й участок | \(\frac<4d> | \(t\) | \(4d\) |
| 3й участок | \(\frac<45d><20t>\) | \(20t\) | \(45d\) |
| Сумма | — | \(25t\) | \(50d\) |
Задача 5*. Первую половину маршрута турист проехал на попутном автомобиле в 10 раз быстрее по сравнению с ходьбой пешком, а вторую половину – на попутном возу в 2 раза медленней. Сэкономил ли турист время на всем маршруте по сравнению с ходьбой пешком?
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | \(10v\) | \(\frac | \(\frac s2\) |
| 2й участок | \(\frac | \(\frac | \(\frac s2\) |
| Сумма | — | \(t=\frac | \(s\) |
п.5. Лабораторная работа №3. Определение средней скорости движения тела
Цель работы
Научиться определять среднюю скорость движения тела по данным измерений на разных участках. Научиться вычислять абсолютные и относительные погрешности при подстановке данных измерений в формулы.
Теоретические сведения
В лабораторной работе изучается движение тела (шарика) по двум участкам (желобам) с различной скоростью.
Длина участков измеряется с помощью мерной ленты с ценой деления \(\triangle=1\) см,
инструментальная погрешность равна: \(d=\frac<\triangle><2>=0,5\) см
Абсолютная погрешность измерений при работе с мерной лентой равна инструментальной погрешности, поэтому: \(\triangle s_1=\triangle s_2=d=0,5\) см
Погрешность суммы двух длин: \(\triangle(s_1+s_2)= \triangle s_1+\triangle s_2=2d=1\) см
Измерение времени на каждом участке проводится в сериях их 5 измерений по методике, описанной в Лабораторной работе №2 (см. §4 данного справочника).
Погрешность суммы двух измерений: \(\triangle(t_1+t_2)=\triangle t_1+\triangle t_2\)
Приборы и материалы
Два желоба (не менее 1 м каждый), шарик, мерная лента, секундомер.
Ход работы
1. Ознакомьтесь с теоретической частью работы, выпишите необходимые формулы.
2. Соберите установку, как показано на рисунке. Установите один желоб под углом, другой – горизонтально, закрепите, поставьте в конце горизонтального участка упор. Подберите длину желобов и наклон так, чтобы движение по каждому участку было не менее 1 с.
3. Измерьте фактическую длину каждого участка движения в готовой установке с помощью мерной ленты.
4. Найдите относительную погрешность суммы двух длин \(\delta_
5. Проведите серии по 5 экспериментов для определения \(t_1\) и \(t_2\) с помощью секундомера.
6. Найдите \(\triangle t_1,\ \triangle t_2, \ \triangle(t_1+t_2),\ \delta_
7. По результатам измерений и вычислений найдите \(v_
8. Сделайте выводы о проделанной работе.
Результаты измерений и вычислений
2) Измерение времени
Цена деления секундомера \(\triangle =0,2\) с
Инструментальная погрешность секундомера \(d=\frac<\triangle><2>=0,1\) с
Время движения по наклонному желобу
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| \(t_1\) c | 1,5 | 1,6 | 1,5 | 1,4 | 1,4 | 7,4 |
| \(\triangle\) c | 0,02 | 0,12 | 0,02 | 0,08 | 0,08 | 0,32 |
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| \(t_2\) c | 2,3 | 2,4 | 2,2 | 2,2 | 2,4 | 11,5 |
| \(\triangle\) c | 0 | 0,1 | 0,1 | 0,1 | 0,1 | 0,4 |
Выводы
На основании проделанной работы можно сделать следующие выводы.
Измерения длин проводились с помощью мерной ленты. Ошибка измерений равна инструментальной ошибке 0,5 см.
Измерения времени проводились с помощью секундомера. По результатам серий экспериментов ошибка была принята равной инструментальной 0,1 с.
Получена величина средней скорости: \begin
Неравномерное движение
В окружающем нас мире редкостью является равномерное движение тел, поскольку большинство объектов материального мира не способны двигаться с подобной точностью на протяжении длительного времени. Потому актуально использование понятия неравномерного движения тел.
Для характеристики такого вида движения используют понятия средней, мгновенной и средней путевой скоростей.
Характеристика средней скорости
Показатель средней скорости рассматривают на определённом отрезке пути, и рассчитывают таким образом:
Поскольку средняя скорость рассчитывается с использованием скалярных величин, то она также есть величиной скалярной.
Среднюю скорость также возможно рассчитать по формуле перемещения:
В этом случае она будет величиной векторной, поскольку рассчитывается через перемещение – векторную величину.
Не нашли что искали?
Просто напиши и мы поможем
Стоит различать эти две скорости. Несмотря на то, что они характеризуют одно и то же движение, данные величины имеют разный физический смысл.
Зачастую, вычисляя среднюю скорость, допускают некоторую погрешность, так как определяют среднюю скорость как среднее арифметическое. Суть заключается в том, что средняя арифметическая величина скорости тела на различных участках может отличаться от реального значения средней скорости тела, рассчитанной через преодоленный путь.
Непрерывное неравномерное движение тел сопровождается постоянным изменением их скорости. Это движение порождает закономерность, которая гласит, что скорость тела в любой следующей точке траектории не равняется его скорости в предыдущей.
Характеристика мгновенной скорости
Мгновенная скорость – это скорость объекта, которая фиксируется в конкретное время в конкретной точке.
Мгновенная скорость, рассчитанная через пройденный путь, есть величиной скалярной. Если она рассчитывается через перемещение, то является величиной векторной.
Характеристика средней путевой скорости
Различают еще одно понятие, характеризующее неравномерное движение – это средняя путевая скорость.
Поскольку средняя скорость – это вектор, который направлен в сторону перемещения тела, то модуль средней скорости принимает значение средней путевой скорости в том случае, когда тело не меняет направление своего движения. Если же тело меняет направление своего движения, модуль средней скорости уменьшается до средней путевой скорости.
Разновидности неравномерного движения
Движение тела может быть неравномерным по скорости и по направлению.
Существует несколько разновидностей неравномерного движения, среди них выделяют:
Сложно разобраться самому?
Попробуй обратиться за помощью к преподавателям
Равнопеременным считается такое неравномерное движение, при котором скорость тела меняется на конкретную величину за равнозначные промежутки времени.
Движение тела, когда его скорость за любые равнозначные промежутки времени не меняется на конкретную величину, является неравнопеременным.
Если при равнопеременном движении скорость тела увеличивается, оно считается равноускоренным, если же скорость тела уменьшается – равнозамедленным.
Неравномерно движущееся тело может сочетать несколько вышеприведенных разновидностей.
Понятие ускорения
Рассчитывается таким образом:
Физический смысл ускорения заключается в том, что оно показывает на какую величину увеличивается или уменьшается скорость тела за единичный период времени.
Данная величина характеризует только равноускоренное или равнозамедленное движение, но не описывает равнопеременное движение, так как при этом не наблюдается взаимозависимость скорости и ускорения тела.
Ускорение со знаком «+» описывает равноускоренное движение, а со знаком «-» – равнозамедленное.
Уравнение ускоренного движения объекта записывается в следующем виде (для оси абсцисс):
С помощью данного уравнения рассчитывают скорость движения тела в любой промежуток времени.