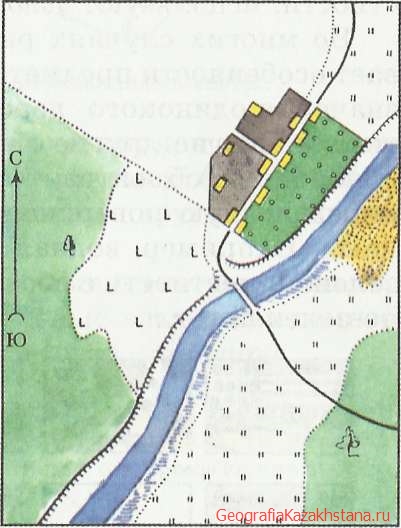
Что такое сплошные горизонтали на плане местности
Страница 4 — 5. План местности — Контурные карты по географии. 6 класс. Дрофа
Комментарий: Перед выполнением работы, обязательно изучите Правила оформления контурных карт. В них вы найдёте информацию о том, как должны быть сделаны надписи к различным географическим объектам. Например, что все водные объекты подписываются синим цветом, а остальные — чёрным.
При этом, если вы внимательно рассмотрите наши ГДЗ, то увидите, что на наших картах объекты подписаны самыми разными цветами. Это сделано специально, ведь наша главная цель — помочь вам сориентироваться в огромном количестве информации, которой насыщена любая карта. Разноцветные надписи помогут вам быстро найти нужное: города и реки, моря и равнины. Вы сможете быстро увидеть что добавилось на карте в результате выполнения следующего задания и лучше понять что и где находится.
Так что пользуйтесь нашими картами «с умом», чтобы ваши оценки не были снижены из-за тонкостей оформления. Работу лучше выполнять по шагам, последовательно выполняя задания к контурным картам. Для того, чтобы увеличить карту, просто нажмите на неё. Также можно увеличивать и уменьшать размер страницы при помощи одновременного клавиш Ctrl и «+» или Ctrl и «-«.
Для выполнения заданий будем рассматривать карту атласа на страницах 8 и 9.
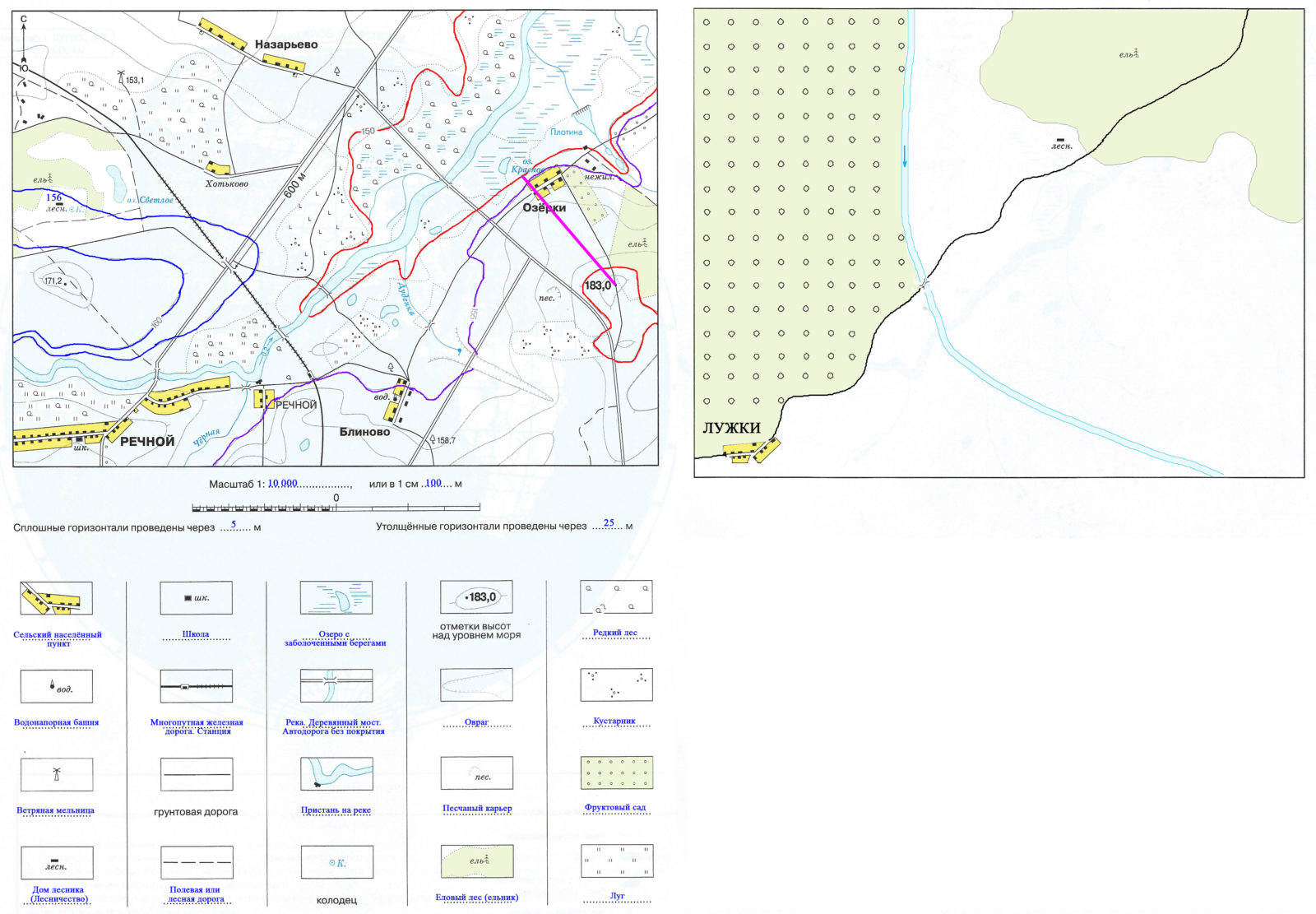
1. Подпишите значения условных знаков.
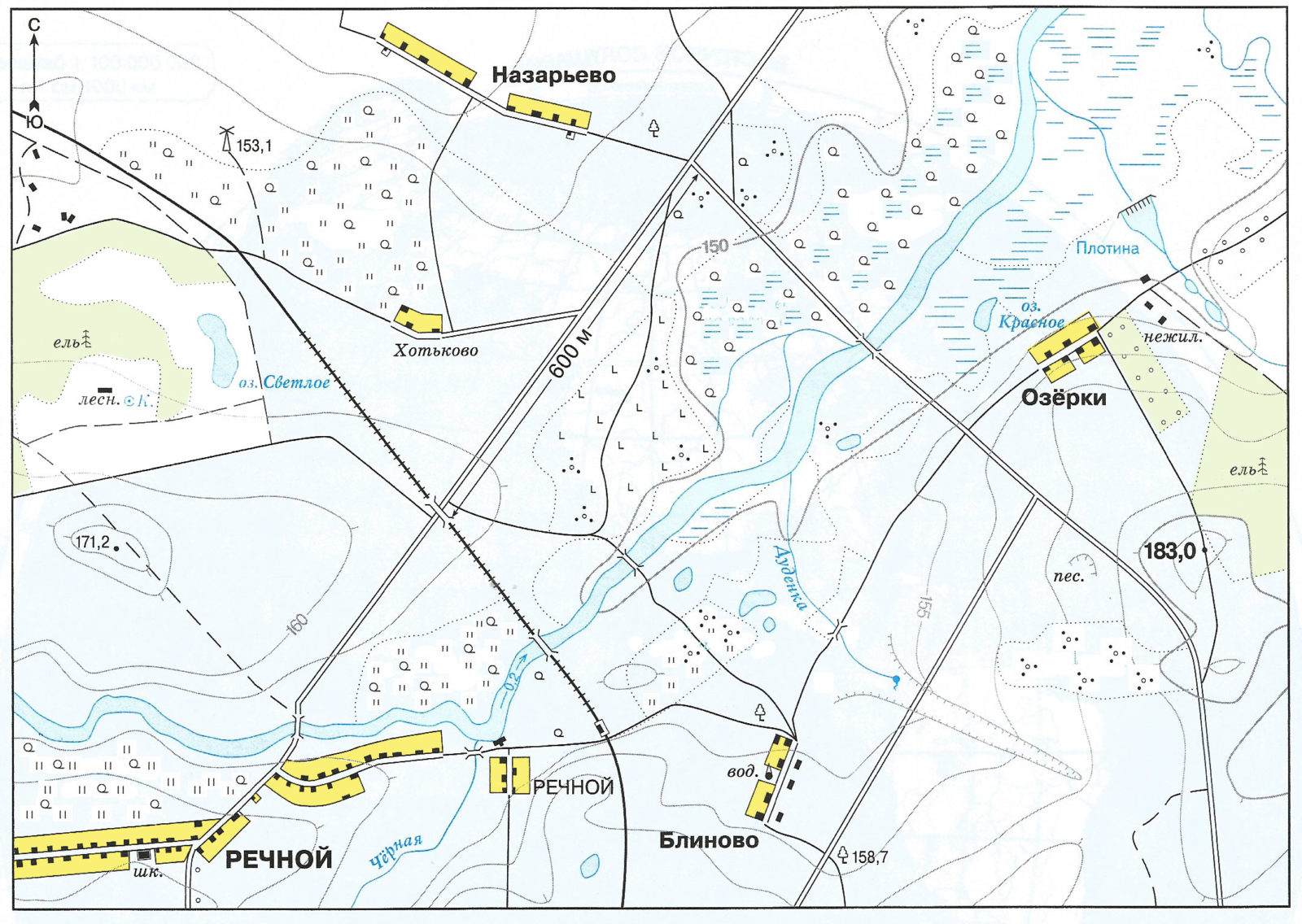
3. Известно, что расстояние на местности от железнодорожного моста до перекрёстка автомобильных дорог составляет 600 м. Определите масштаб плана и впишите его в легенду плана.
Измерим это расстояние на карте линейкой. Получается, что 600 метров на местности = 6 см на карте. Значит 1 см на карте равен 100 метрам на местности. Переведем метры в сантиметры: 100 м = 10 000 см, то есть масштаб карты 1:10 000.
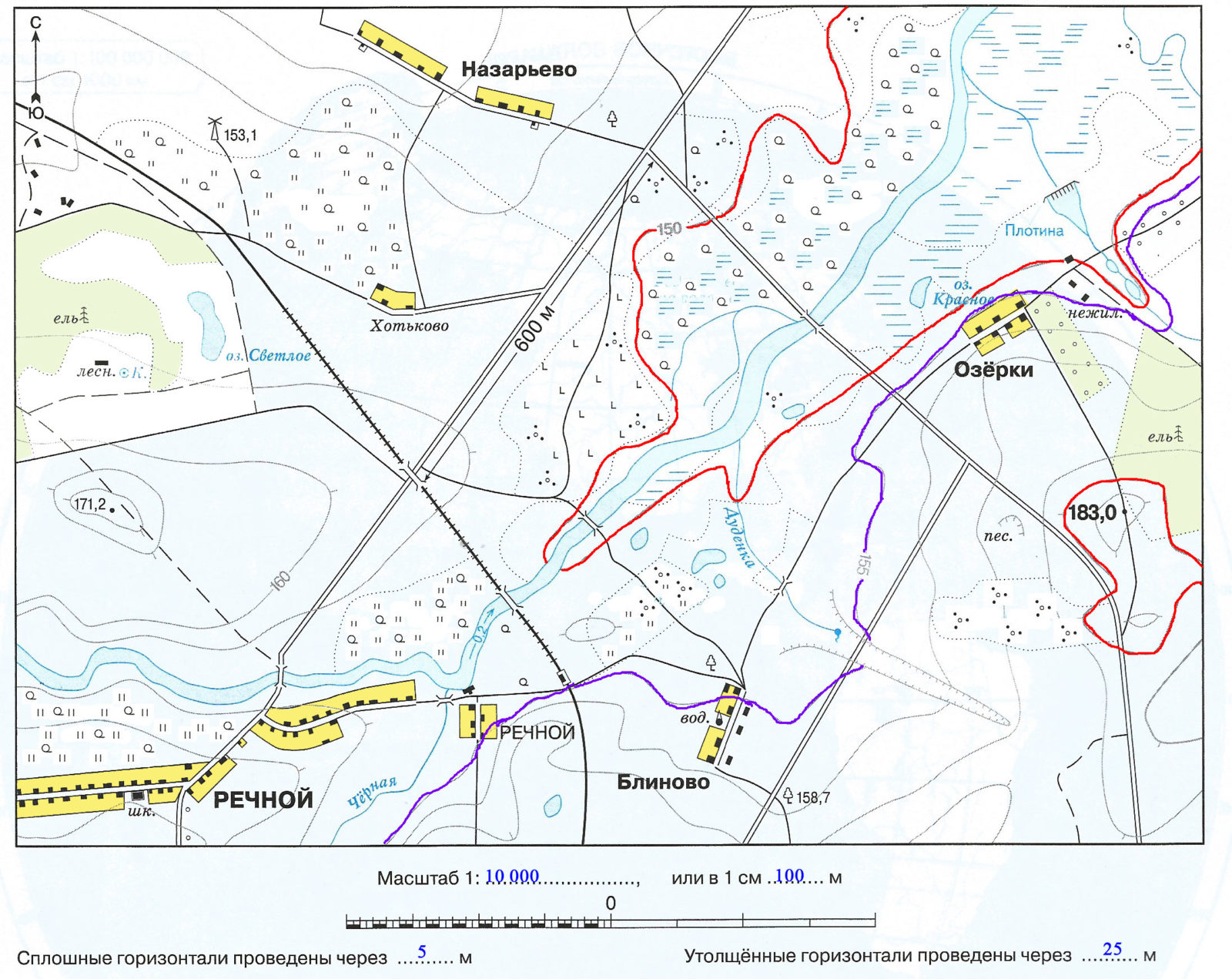
4. Определите, через сколько метров проведены сплошные и утолщённые горизонтали, и укажите их в легенде плана.
Рассмотрим карту. Для удобства обведём утолщенные горизонтали красной линией, а ближайшую сплошную горизонталь с обозначением высоты — фиолетовой линией.
Мы видим, что красная горизонталь с отметкой расположена на уровне 150 м, а ближайшая к ней фиолетовая — на уровне 155 м. Значит расстояние между сплошными горизонталями на этой карте составляет 5 метров.
По правилам, утолщенные диагонали проводятся по каждой пятой сплошной горизонтали. То есть расстояние между утолщенными горизонталями составляет 5 • 5 = 25 м. Можно вычислить, что вторая обведенная нами красным цветом утолщенная горизонталь находится на высоте 150 + 25 = 175 м.
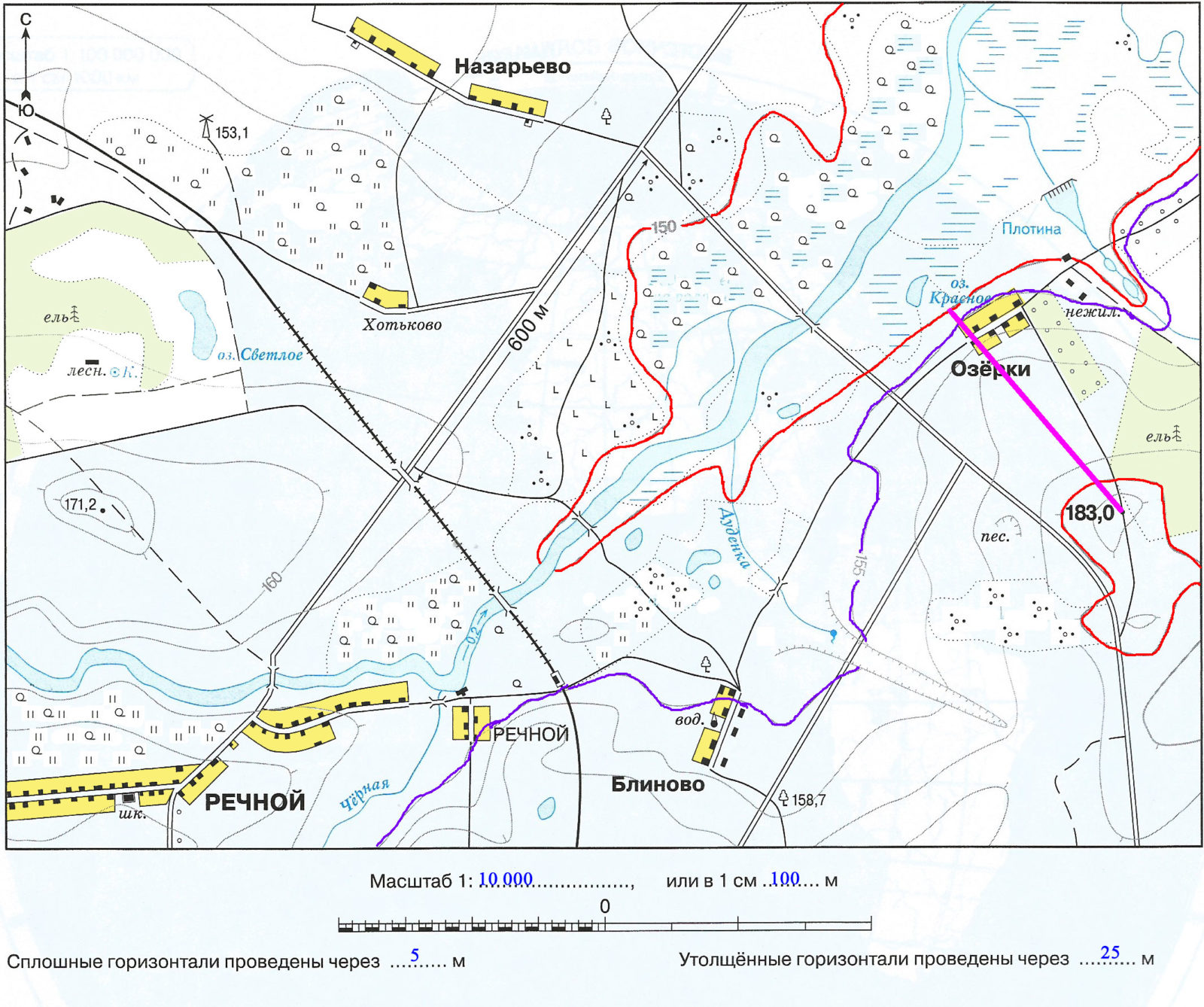
5. Определите максимальную и минимальную абсолютные высоты, подписанные на плане. Проведите между ними линию и подпишите расстояние между отметками высот. Определите относительную высоту.
6. Определите и подпишите абсолютную высоту домика лесника, расположенного в западной части плана.
Для удобства обведём ближайшие к домику лесника горизонтали синими линиями. Мы видим, что горизонталь, расположенная выше домика лесника имеет отметку 160 метров. Так как расстояние между сплошными горизонталями составляет 5 метров, то горизонталь, расположенная ниже домика лесника находится на отметке 155 м.
Можно предположить, что домик лесника находится на высоте 156 метров над уровнем моря.
7. Составьте план местности по описанию:
«От посёлка Лужки, расположенного на юго-западе, к хвойному лесу, расположенному на северо-востоке, ведёт грунтовая дорога. Примерно на середине пути к лесу протекает небольшая речка, перебраться через которую можно по деревянному мосту. Речка течёт с севера и вскоре после моста поворачивает на юго-восток. От посёлка и до речки, слева от дороги, тянутся фруктовые сады. На самом краю леса, к северу от дороги, стоит избушка лесника».
План местности
Как обозначаются предметы местности на плане? Какова польза плана в хозяйственной деятельности человека?
Рис. 16. План местности.
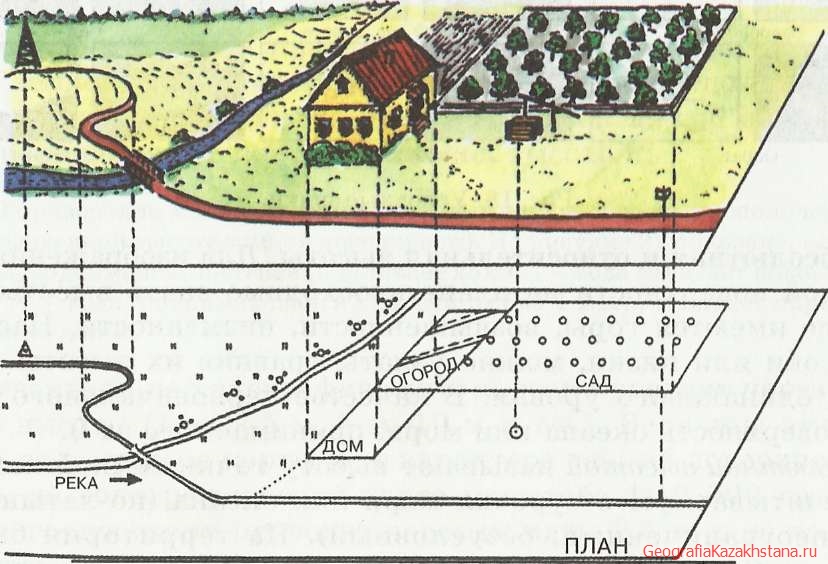
Рис. 17. Нанесение предметов местности на план.
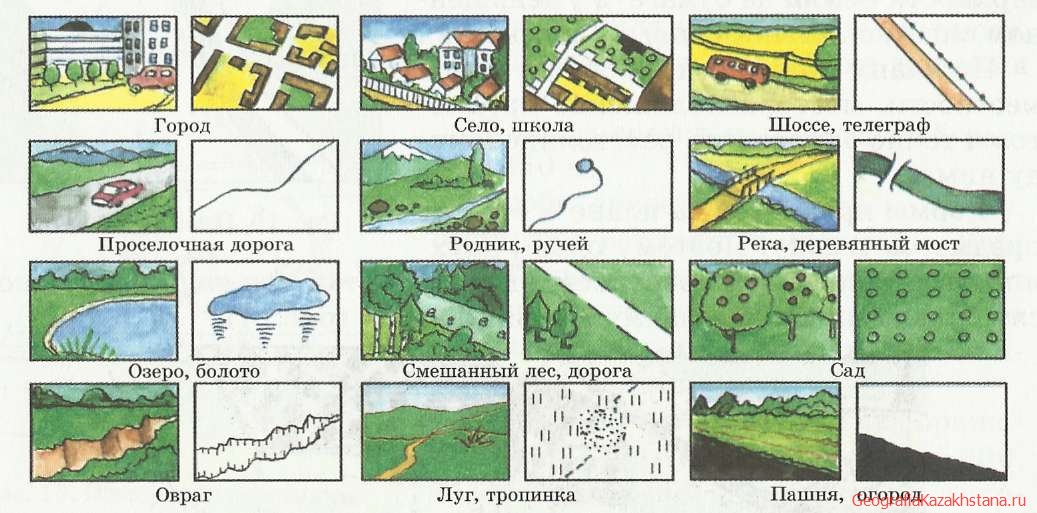
2. Условные знаки. Чтобы различить предметы на плане, возникает необходимость сверху написать их названия. Но тогда весь чертеж состоял бы из надписей. И было бы трудно понять такой чертеж. Поэтому, для того чтобы было легко представить характер местности, используют условные знаки (рис. 18).
Рис. 18. Условные знаки.
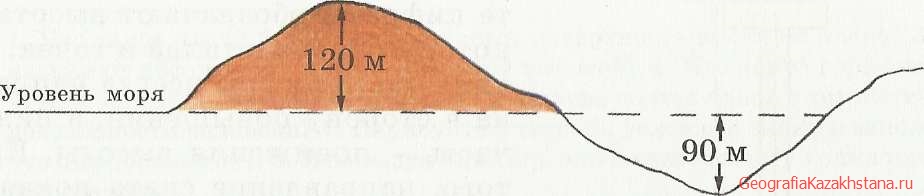
Рис. 19. Положительные и отрицательные абсолютные высоты.
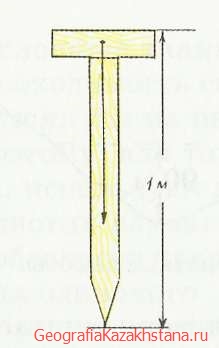
Рис. 20. Нивелир.
Простейший нивелир можно легко изготовить самим. На верхнюю часть рейки высотой 1 м горизонтально прибивают деревянную планку. На ней устанавливают отвес на шнуре, который используют для проверки правильности уровня планки (рис. 20).
Для определения высоты холма один ученик, стоя у подошвы холма, направляет нивелир к его склону. Второй ученик вбивает колышек в указанное место. Это означает, что место забитого колышка от нивелира находится на 1 м выше. Далее нивелир переносят к колышку и направляют на следующую точку. Таким образом, перемещаясь вверх по склону, определяют относительную высоту вершины холма от его подошвы (рис. 21).
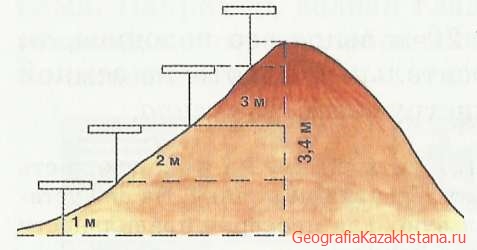
Рис. 21. Измерение высоты холма.
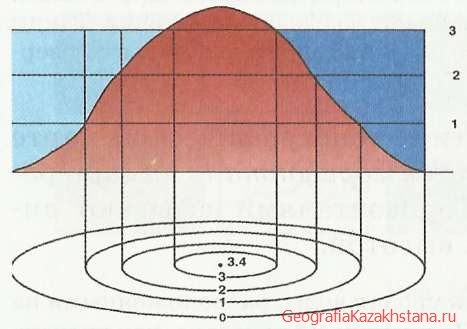
Рис. 22. Изображение холма горизонталями.
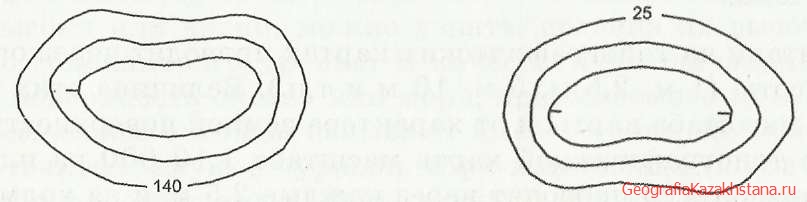
Рис. 23. Определение различия форм рельефа по цифрам и бергштриху. Расположение цифр показывает повышение и понижение высоты местности.
Некоторые формы земной поверхности (обрывы, овраги и т. д.), которые невозможно обозначить горизонталями, изображают с помощью дополнительных условных знаков.
5. Значение плана для деятельности человека. План очень необходим в ежедневной жизни. Перед тем, как начать любое крупное строительство завода, фабрики и гидроэлектростанции, нужно начертить план той местности. Чтобы проложить дорогу, построить здание, нужен план. Специалист сельского хозяйства также планирует посевные работы. План помогает ориентироваться на местности во время туристических походов и путешествий. Поэтому умение разбираться в плане, наносить его на бумагу при необходимости приносит очень большую пользу.
2. Как изображается поверхность земли на плане?
3. Что называют абсолютной и относительной высотой?
4. Что такое горизонтали? 5.
Для чего используется бергштрих?
6. Какова польза плана в хозяйственной деятельности человека?
7. Нарисуйте в тетради условные знаки и запомните, что они обозначают.
8. Используя нивелир, определите высоту холма или глубину оврага.
Сущность изображения на картах рельефа горизонталями учебные материалы
↑ Формы рельефа. Характеристика скатов.
Рельеф земной поверхности, представляет собой совокупность различных по форме и размерам неровностей. К основным типовым формам рельефа относятся:
гора; горный хребет; котловина; лощина; седловина.
При сравнении между собой изображения горы и котловины видно, что они выглядят на карте одинаково – как система замкнутых, огибающих одна другую кривых линий. Схожими между собой получаются также изображения хребта и лощины. Все формы рельефа ограничены поверхностями (скатами). Скаты, в зависимости от характера их профиля, подразделяются на ровные, выпуклые, вогнутые и волнистые. Каждая форма скатов характеризуется своеобразием изображения скатов горизонталями. Поэтому, необходимо уметь различать типовые формы рельефа и формы скатов, изображенные на карте горизонталями, т.е. уметь читать рельеф на карте.
Ровный скат характеризуется одинаковой крутизной на всем его протяжении и хорошо просматривается с гребня. Изображение ровного ската горизонталями отличается равенством заложений.
Выпуклый скат круче в нижней части и положе в верхней. Нижняя часть выпуклого ската с гребня не просматривается. Изображение выпуклого ската горизонталями характеризуется увеличением заложений от его нижней части к верхней.
Вогнутый скат круче в верхней части и положе в нижней. Он просматривается с гребня на всем протяжении. Изображение вогнутого ската горизонталями характеризуется увеличением заложений от верхней его части к нижней.
Волнистый скат представляет сочетание ровных, выпуклых, и вогнутых скатов. Соответственно и изображение волнистого ската горизонталями будет чередоваться различными величинами заложений. Линия, где скат переходит от более пологого к более крутому или наоборот, называется перегибом ската.
Способ изображения рельефа горизонталями позволяет изучать и оценивать тактические свойства местности, а именно проходимость местности, защитные и маскировочные свойства местности, а также наблюдение и ведение огня и возможности инженерных расчетов на оборудование позиций в подразделениях и частях.
Определение направления скатов.
Направлением ската называется простирание его наибольшей крутизны.На карте это направление перпендикулярно к горизонтали, проходящей через данную точку на скате.
Таким образом, чтобы определить по карте направление ската в какой – либо точке, лежащей на горизонтали, надо в этой точке восстановить в виде короткой черточки (штриха) перпендикуляр к горизонтали в сторону понижения ската. Для определения направления ската в любой точке, находящейся между горизонталями, следует провести через нее прямую или кривую (в зависимости от формы горизонталей) линию пересекающуюся приблизительно под прямым углом ближайшие в обе стороны от этой горизонтали. Эта линия и будет указывать направление ската.
↑ Определение крутизны ската
Рельеф местности, являясь одним из важнейших топографических элементов местности, оказывает существенное влияние на боевые действия войск. Поэтому на топографических картах, кроме местных предметов, изображаются также и неровности земной поверхности, без чего невозможно всесторонне изучать характер местности, ее пространственные формы и производить по карте необходимые расчеты.
Чтобы отчетливо и полно представлять себе местность по карте, необходимо прежде всего хорошо разбираться в изображении на ней рельефа.
В 15 – 17 веках применялся перспективный или картинный способ изображения рельефа.
Затем стал применяться расчетно – перспективный способ.
В конце 18 столетия появился способ изображения рельефа штрихами, сущность которого заключалось в том, что скаты возвышенностей изображались на картах черточками (штрихами) различной толщины, чем круче скат, тем толще и короче штрих, чем положе скат, тем тоньше и длиннее штрих и больше расстояние между штрихами.
Сущность этих способов сводилась к созданию впечатления крутизны скатов, путем изменения расстояния между штрихами или густоты тона краски. Более крутые скаты изображались краской более густого тона; при переходе к менее крутым скатам тон краски ослабевался.
К недостаткам штрихового способа изображения рельефа нужно отнести его чрезвычайную трудоемкость, а также невозможность определения по штриховому изображению высот точек местности и превышений между ними. Кроме того, сплошная штриховка затемняла карту и затрудняла ее чтение. Отмывка более проста для выполнения, чем штриховка. Однако изображение рельефа этим способом, хотя и обладает наглядностью, но не дает возможности производить по карте какие – либо расчеты и измерения. На обзорно – топографических картах отмывка применяется главным образом как вспомогательное средство, которое улучшает наглядность изображения рельефа.
Во второй половине 19 века возросшие требования к содержанию карт обусловили необходимость более точного изображения рельефа на картах, в результате чего был разработан более современный способ изображения рельефа – горизонталями, который постепенно заменил штриховку и получил общее признание.
Приоритет в деле внедрения способа горизонталей принадлежит русским военным топографам, которые уже более ста лет назад стали применять этот способ для изображения рельефа на картах. Полный перевод на этот способ совершен в России в 1867 году, когда во всех остальных европейских странах господствовал еще устаревший способ – штриховка.
На топографических картах способ изображения рельефа горизонталями нашел дальнейшее развитие, обеспечивающее точную и правильную передачу характерных особенностей всех форм рельефа.
Таким образом изображение рельефа горизонталями позволяет наглядно показать на карте все неровности земной поверхности и обладает высокими измерительными свойствами, благодаря чему можно решать различные задачи как в интересах войск, так и для нужд народного хозяйства.
Оттенение скатов неровностей тонами серо – коричневой или оранжевой краской на картах масштаба 1: 500 000 и 1: 1 000 000 значительно улучшает изображение и читаемость рельефа. Горизонталями на карте называются кривые замкнутые линии, соединяющие точки местности с одинаковой высотой. Для лучшей читаемости горизонтали изображаются на картах коричневым цветом.
Этот способ является основным при изображении рельефа на современных картах, т.к. такое изображение рельефа обладает высокими измерительными свойствами.
По расположению горизонталей можно судить о крутизне скатов. Чем круче скат, тем горизонтали расположены ближе одна к другой, и наоборот, чем положе скат, тем горизонтали расположены дальше одна от другой.
Достоинства способа изображения рельефа горизонталями состоит в том, что он позволяет получить по карте такое изображение рельефа, по которому можно решать следующие задачи:
строить вертикальные разрезы местности в любых направлениях;
воспроизводить рельеф местности в виде макетов;
вычислять объем земляных работ;
составлять проекты различных сооружений и другие задачи, требующие знания высот точек местности, превышений между ними и крутизны скатов.
↑ В войсках по карте можно решать следующие задачи:
производить выбор участков местности для размещения боевых порядков частей;
производить выбор площадок для позиций подразделений;
определять возможность ведения огня по маловысотным самолетам противника;
определять места для маскировки личного состава и техники от наблюдения противника;
Недостатком способа изображения рельефа горизонталями является то, что он обладает достаточной наглядностью и пластичностью. Горизонтали не всегда позволяют создать впечатление сплошной поверхности, поэтому по ним трудно судить о формах рельефа и соотношениях высот. Этот недочет частично исправляется согласованием рисунка смежных горизонталей, выделением в рельефе главного за счет исключения мелких подробностей и различными пояснительными подписями, характеризующими элементы рельефа.
Выбор высоты сечения для изображения рельефа местности горизонталями зависит от масштаба, в котором составляется карта и от характера рельефа.
На картах высоту сечения непосредственно не видно, она подписывается под линейным масштабом карты. На картах мы видим заложения, т.е. расстояния между двумя горизонталями. Заложение, есть проекция наклонного отрезка, т.е. наикратчайшее расстояние между двумя смежными горизонталями.
Виды горизонталей: основные, дополнительные (половинные), вспомогательные.
Горизонтали, соответствующие принятой высоте сечения, называются основными и проводятся сплошными линиями.
Они проводятся только в тех местах, где ими нужно выразить какие – либо детали рельефа.
При изображении полугоризонталями вершин, расположенных на скатах, обязательно проводятся ответные полугоризонтали, т.е. те же горизонтали, но на встречных скатах.
В тех же случаях, когда важные в каком – либо отношении детали рельефа не выражаются и полугоризонталями, применяются вспомогательные горизонтали.
Проводятся они также прерывистыми линиями, но более короткими штрихами, нежели половинные горизонтали. Половинные, вспомогательные и утолщенные горизонтали, так же как и основные изображаются на картах коричневым цветом.
Основная высота сечения всегда указывается под линейным масштабом карты. Здесь подписывается через сколько метров проведены сплошные горизонтали.
Горизонтали и их свойства. Способы построения горизонталей



По отметкам точек
Рельефом называют совокупность неровностей земной поверхности. Знание рельефа местности необходимо при проектировании и строительстве железных и автомобильных дорог, осушительных и оросительных систем, промышленных предприятий и т. д. Существует несколько способов изображения рельефа на топографических картах и планах. Наиболее старый способ – это изображение рельефа штрихами, наносимым на карту по особой шкале.
Рельеф местности может быть также изображен подписями отметок ряда точек или отмывкой красками различного тона. Однако наилучшим способом оказалось изображать рельеф горизонталями в сочетании с некоторыми условными знаками и подписями отметок характерных точек. Горизонталь – это линия, соединяющая точки земной поверхности с одинаковыми высотами.
Чтобы правильно изобразить рельеф, необходимо знать его основные формы.
Существует пять основных форм рельефа (рисунок 3.5):
— возвышенность (рисунок 3.5, а);
— котловина (рисунок 3.5, б);
— хребет (рисунок 3.5, в);
— лощина (рисунок 3.5, г);
— седловина (рисунок 3.5, д).
На рисунке 3.5 эти формы рельефа показаны в разрезе. Рассмотрим сущность изображения рельефа горизонталями. На рисунке 3.5, а показана возвышенность (холм, гора), наивысшую точку которой называют вершиной, низ – подошвой, а боковые поверхности – скатами. Для изображения возвышенности горизонталями представим себе, что эту возвышенность пересекают ряд равноотстоящих друг от друга плоскостей, параллельных основной уровенной поверхности. Линии пересечения этими плоскостями земной поверхности и будут являться горизонталями. Спроектировав их отвесными линиями на плоскость, получим на ней изображение возвышенности.
Для наглядности некоторые горизонтали подписывают, кроме того у них ставят черточки-бергштрихи, показывающие направление ската местности.
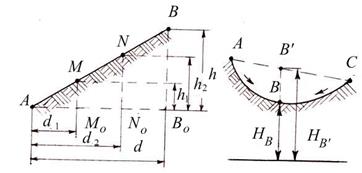
Расстояние между двумя соседними секущими плоскостями называют высотой сечения рельефа h. На картах и планах высота сечения рельефа характеризуется разностью высот двух смежных горизонталей. Например, на рисунке 3.5, а высота сечения рельефа h = 5 м.
Расстояние между горизонталями на плане или карте называется заложением. На рисунке 3.5, а заложение d = АС. Зависимость между высотой сечения рельефа h, заложением d, углом наклона υ, уклоном i и линии местности АВ можно получить из треугольника АВС (рисунок 3.5, а):
Уклон и угол наклона линии местности являются основными характеристиками крутизны скатов. Чем больше угол наклона, тем круче скат местности. Из формулы (3.6) следует, что чем меньше заложение d или чем чаще горизонтали на плане, тем скат местности круче.
Изображение горизонталями котловины, лощины, хребта и седловины показано на рисунке 3.5. Котловина (впадина) – замкнутое углубление поверхности (см. рисунок 3.5, б). Самую низкую часть впадины называют дном, боковые поверхности – скатами, а линию слияния с окружающей местностью – бровкой.
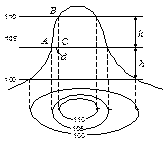 а) а) |  б) б) |
 в) в) |  г) г) |
 д) д) |
Рисунок 3.5 – Основные формы рельефа
Хребет – вытянутая в одном направлении возвышенность с двумя скатами (см. рисунок 3.5, в). Линию встречи скатов в верхней части называют водоразделом (водораздельной линией).
Лощина – вытянутое в одном направлении понижение с двумя скатами (рисунок 3.5 г). Линию встречи скатов в нижней их части называют водосливом или тальвегом (водосливной линией).
Седловина – понижение между двумя возвышенностями (см. рисунок 3.5 д). Наиболее низкую точку между возвышенностями называют перевалом.
Бергштрихи на картах и планах обычно показывают по водораздельным и водосливным линиям. Подписи на горизонталях делают так, чтобы основание числа показывало направление ската. Горизонтали вычерчивают коричневым цветом. Каждую десятую или пятую из них вычерчивают утолщенной линией.
Из сущности горизонталей вытекают их свойства:
— горизонталь – это замкнутая кривая линия, все точки на которой имеют одинаковую высоту, кратную высоте сечения рельефа;
— горизонтали на плане не могут раздваиваться и обрываться; если горизонталь не замыкается в пределах плана, она замыкается за его пределом;
— горизонтали не должны пересекаться между собой, так как они получаются пересечением земной поверхности плоскостями, лежащими на разных высотах;
— чем чаще горизонтали на плане, тем уклон местности больше, или чем меньше заложение, тем скат круче;
— водораздельные и водосливные линии и направления максимального уклона горизонтали пересекают под прямым углом.
Высота сечения рельефа устанавливается в зависимости от масштаба плана и характера рельефа местности так, чтобы горизонтали не сливались между собой. В Республике Беларусь приняты следующие высоты сечения рельефа при масштабах съемки:
| 1:500 – h = 0,25; 0,5 м; 1:1000 – h = 0,25; 0,5; 1 м; 1:2000 – h = 0,5; 1; 2 м; | 1:5000 – h = 0,5; 1; 2; 5 м; 1:10000 – h = 1; 2,5; 5 м. |
Для более полного изображения и удобства чтения рельефа на картах и планах подписывают отметки характерных точек рельефа (вершин холмов, дна котловин, перевалов и т. д.). Например, на рисунке 3.5, б подписана отметка дна котловины 98,7 м.
Способы построения горизонталей по отметкам точек.
Для проведения горизонталей на плане нужно нанести характерные точки, снятые на местности, и выписать их высоты. Те точки, между которыми земная поверхность не имеет переломов, т. е. имеет постоянный уклон, соединить линиями. Далее на каждой линии интерполированием находят точки пересечения ее горизонталями и отмечают высоты этих горизонталей.
Соединив затем плавными кривыми линиями точки с одинаковыми высотами, получают изображение рельефа местности на плане. Таким образом, задача построения горизонталей на плане в основном сводится к умению находить проекции точек пересечения горизонталями линий, отметки концов которых известны, при этом высота сечения рельефа должна быть уже установлена. Эта задача называется интерполированием горизонталей, т. е. нахождением промежуточных значений высот горизонталей по отметкам точек. Интерполирование можно производить аналитическим или графическим способом.
Аналитический способ. По известным высотам точек А и В и расстоянию d между ними (рисунок 3.6, а) необходимо найти величины расстояний d1 и d2 от точки А до точек М0 и N0 c отметками Нм и HN, равными отметкам горизонталей.
Рисунок 3.6 – Аналитический способ интерполирования
Из подобия треугольников АВВО, АММО и ANNO находим:
Графический способ. Интерполирование этим способом выполняют с помощью миллиметровой или прозрачной бумаги. При наличии миллиметровой бумаги ее прикладывают к линии плана АВ. По отметкам концов АВ строят профиль этой линии. Проектируя затем на линию плана точки пересечения линии профиля с линиями миллиметровой бумаги, принятыми за секущие плоскости, получают искомые точки М и N.
При наличии прозрачной бумаги (восковки, кальки), на ней предварительно наносят ряд равноотстоящих друг от друга параллельных линий, которым придают отметки секущих плоскостей. Восковку накладывают на план так, чтобы конечные точки линии плана заняли положение, соответствующее их отметкам между линиями восковки (рисунок 3.7). Далее точки пересечения линии плана с линиями восковки перекалывают на план. Это и будут искомые точки на плане.
Решение инженерных задач по планам и картам
Современные топографические карты и планы дают богатый и разносторонний материал о той местности, которая на них изображена условными знаками. Зная условные знаки, при изучении карты можно получить необходимые данные о населенных пунктах, гидрографии, растительности, дорожной сети, рельефе и других объектах. Кроме того, при помощи карты можно решать ряд инженерных задач: определять географические и прямоугольные координаты точек, измерять дирекционные углы и азимуты направлений, определять высоты точек, уклоны заданных линий, водосборные площади бассейнов, строить профили земной поверхности, производить трассирование и т. д.
1. Прямоугольные координаты точек на карте определяют от линии координатной (километровой) сетки, абсциссы и ординаты которых подписываются в общегосударственной системе координат.
2. На картах подписываются также широты и долготы точек пересечения параллелей и меридианов, ограничивающих данный лист. Кроме того, на обрамляющих карту рамках вычерчиваются одноминутные деления широты и долготы. Соединяя точки одноименных делений северной и южной сторон рамок, а также западной и восточной, получим на карте сетку меридианов и параллелей, пользуясь которой, можно определить широту и долготу любой точки карты.
3. Дирекционный угол или азимут линии можно измерить транспортиром непосредственно на карте, как угол между направлением линии километровой сетки или истинного меридиана и направлением заданной линии. Обычно на полях карты всегда дается для данного листа сближение меридианов и склонение магнитной стрелки, используя которые, по формулам (2.3) – (2.4) можно вычислить все углы ориентирования.
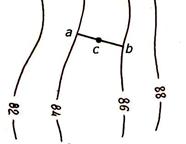
4. Высоту (отметку) любой точки, например С (рисунок 3.8, а), можно определить, если через нее провести линию ab по кратчайшему расстоянию между горизонталями.
Из подобия треугольников abb1 и acc1, учитывая, что h – высота сечения рельефа, d – заложение (рисунок 3.8, б), получим cc1 = ac bb1 / ab или Δh = Δd h /d. (3.7)
Отметка точки НС будет равна отметки точки a плюс величина Δh:
|  б) б) |
Рисунок 3.8 – Определение отметки точки
В формуле (3.7) величины d и Δd измеряют на плане, а высота сечения рельефа известна на плане или карте.
5. Определяют уклон линии. Уклоном линии называется тангенс угла наклона этой линии или отношение высоты сечения рельефа к заложению (рисунок 3.8, б):
Для определения уклона можно воспользоваться формулой (3.6) или (3.8). Из формул следует, что уклон – безразмерная величина. Его выражают в процентах (% – сотых долях) или в промилях (‰ – тысячных долях). Для определения угла наклона линии (крутизны ската) υ из формулы (3.8) можно получить:
υ = arctg i = arctg (h / d). (3.9)
Угол наклона можно также определить графически с помощью графика заложений, который обычно приведен под южной рамкой карты. При отсутствии графика заложений его можно построить. Для этого на горизонтальной прямой АВ от точки А откладывают равные отрезки произвольной величины (рисунок 3.9). Из точек отложения к прямой АВ восстанавливают перпендикуляры. Используя формулу (3.8), определяют заложение:
d = h / tg υ = h / i, (3.10)
где h – высота сечения рельефа
Подставляя в формулу (3.10) величины υ, равные 1, 2, 3 о и т. д., последовательно получают заложение для каждого из углов наклона υ и откладывают их на перпендикулярах в масштабе плана или карты. Полученные на перпендикулярах точки соединяют плавной кривой линией, а внизу подписывают углы наклона.
6. Для построения по заданному направлению АВ на плане профиля линии местности при помощи полоски бумаги линия с плана переносится на миллиметровую бумагу с отметками всех точек пересечения линии с горизонталями. Далее в заданном вертикальном масштабе по вертикальным линиям откладывают отметки точек, и все вершины перпендикуляров соединяют прямыми линиями. Получают профиль местности по заданному направлению (рисунок 3.10).
7. Для проведения на карте или плане линии заданного уклона по графику заложений или, исходя из формулы (3.10), определяют величину заложения соответствующего уклона. Затем циркулем-измерителем откладывают это заложение в масштабе плана и, начиная от первой горизонтали, пересекающей линию, последовательно засекают смежные горизонтали. Полученная ломаная линия будет иметь заданный уклон (рисунок 3.11).
 |
Рисунок 3.10 – Продольный профиль
8. Водосборные площади по картам и планам определяют для вычисления расхода воды с бассейнов при строительстве плотин, мостов, труб и т. п. Водосборной площадью или бассейном водотока называют ту площадь, с которой поверхностные воды после дождя или таяния снега по условиям рельефа местности и его геологического строения стекают в данный водоток. Границами водосборной площади служат водораздельные линии и линии наибольшего ската. На карте или плане сначала намечают границы водосборной площади до створа строящегося сооружения, а затем при помощи планиметра или палетки определяют площадь в пределах установленной границы (рисунок 3.12).
|  | |
| Рисунок 3.11 – Линия заданного клона | Рисунок 3.12 – Определение границы водосборной площади |
Решение практических задач на планах и картах подробно изложено в учебно-методических пособиях по выполнению расчетно-графических и лабораторных работ по геодезии.
Определение площадей по картам и планам
При решении многих вопросов, связанных с использованием земельной территории, необходимо знать площади тех или иных участков. Площади участков могут быть определены или по результатам обмера участка в натуре или по планам и картам.
Существует три основных способа определения площадей:
— графический, когда площадь вычисляется по данным, взятым графически с плана или карты;
— аналитический, когда площадь вычисляют непосредственно по результатам полевых измерений или по их функциям – координатам вершин участка;
— механический, когда площадь определяется по плану при помощи специальных приборов, называемых планиметрами.
Часто эти способы применяются комбинированно. Например, общая площадь участка определяется аналитическим способом, а площадь внутренних контуров – графическим или механическим. Рассмотрим каждый из вышеуказанных способов более подробно.
Графический способ определения площадей. Сущность этого способа состоит в том, что данный участок на плане разбивают прямыми линиями на ряд простейших геометрических фигур (обычно треугольники, реже – прямоугольники, квадраты или трапеции) и с помощью циркуля-измерителя и масштабной линейки определяют в каждой фигуре размеры тех элементов, которые необходимы для вычисления площади фигуры.
Вычислив по известным формулам геометрии площади фигур и взяв их сумму, находят общую площадь участка. Ошибка определения площади графическим способом равна примерно 1:100 – 1:200 от величины вычисляемой площади. Для повышения точности определения площадей этим способом следует пользоваться планами наиболее крупного масштаба, а также использовать, где это возможно, данные измерений в натуре.
Площади криволинейных контуров удобно определять при помощи палеток. Палетка (рисунок 3.13) представляет собой сетку квадратов, нанесенную на восковке или прозрачной целлулоидной пластинке. Стороны квадратов могут быть от 2 до 10 мм. Пользование палеткой видно из рисунка 3.13. Для определения площади палетку накладывают на контур и считают число квадратов, поместившихся внутри контура.
Доли неполных квадратов при этом оценивают на глаз. Зная в масштабе плана площадь одного квадрата, умножением на число квадратов находят общую площадь контура. Точность определения площадей палеткой несколько ниже, описанного выше графического способа. Главная ошибка при этом происходит от оценки частей неполных квадратов на глаз. Более высокую точность дают палетки с меньшей стороной квадрата.
Аналитический способ определения площадей. Исходными данными для вычисления площадей данным способом служат координаты вершин многоугольника.
Пусть требуется вычислить площадь полигона 1-2-3-4 (рисунок 3.14), координаты вершин которого известны: 1 (X1, Y1); 2 (Х2, Y2); 3 (Х3, Y3); 4 (Х4, Y4). Из рисунка 3.14 видно, что площадь Р данного четырехугольника представляет собой алгебраическую сумму и разность площадей трапеции:
Раскрыв скобки, выполнив сокращение и приведение подобных членов, получим:
или в общем виде для n-угольника можно записать
Подобным образом из уравнения (3.11) после преобразований можно получить:

Согласно формулам (3.12) и (3.13) двойная площадь многоугольника равна сумме произведений всех абсцисс на разность ординат последующей и предыдущей вершин, или сумме произведений всех ординат на разность абсцисс предыдущей и последующих вершин.
Следует иметь ввиду, что сумма всех разностей абсцисс (или ординат) от первой до последней точки должна равняться нулю. Это свойство используется для контроля вычисления разностей в формулах (3.12) и (3.13). Погрешность вычисления площадей аналитическим способом не превышает 1:1000 вычисляемой площади.
Механический способ определения площадей. Определение площадей механическим способом производится при помощи планиметров. Наибольшее распространение получил полярный планиметр (рисунок 3.15), состоящий из полюсного и обводного рычагов.
Полюсный рычаг на одном конце имеет груз с короткой иглой (полюсом), а на другом – штифт, который соединяется с обводным рычагом. На конце обводного рычага имеется обводной шпиль (или лупа), которым обводят измеряемую площадь. На обводном рычаге расположен счетный механизм (рисунок 3.15), состоящий из счетного колеса, разделенного на 100 частей. Ось вращения колеса сопряжена при помощи червячной передачи с циферблатом, разделенным по окружности на 10 частей и снабженным указателем для снятия отсчета.
Червячная передача устроена так, что одному обороту колеса соответствует поворот циферблата на одно деление. Рядом с колесом находится верньер, по которому отсчитывают десятые доли делений колеса или тысячные доли его оборота.
Полный отсчет, выраженный в тысячных долях оборота колеса, состоит из четырех цифр, первая из которых берется по указателю циферблата, вторая и третья – по нулевому штриху верньера с ободка колесика. Четвертая отсчитывается по верньеру. Например, отсчет на рисунке 3.15 составит 3215.
При определении площади фигуры устанавливают планиметр полюсом внутри или вне контура фигуры, а обводной шпиль ставят над какой-либо точкой контура и делают отсчет по счетному механизму U1. После этого тщательно обводят шпилем по ходу часовой стрелки контур фигуры и делают второй отсчет U2. Площадь Р при полюсе вне фигуры вычисляют по формуле
а при полюсе внутри фигуры –
где С – цена деления планиметра;
g – постоянное число планиметра.
Перед работой планиметр необходимо поверить и определить его цену деления и постоянное число.
При проверке планиметра должны быть проверено выполнение следующих условий:
— счетное колесо планиметра должно свободно вращаться на оси без трений и колебаний. Выполнение этого условия достигается регулировкой подшипников оси колеса при помощи исправительных винтов.
— плоскость ободка счетного колеса должна быть перпендикулярна к оси обводного рычага. Для проверки этого условия обводят одну и ту же фигуру при двух положениях планиметра, когда счетный механизм находится слева и справа от фигуры. Если расхождение между разностями отсчетов в обоих случаях не превышает 2-3 делений планиметра, то условие выполнено. В противном случае площадь следует определять при двух положениях планиметра и брать среднее из результатов.
Цену деления планиметра определяют многократными обводами двух-трех квадратов координатной сетки плана или карты при двух положениях планиметра, помещая полюс вне фигуры.
Тогда цена деления будет равна известной площади обводимой фигуры Р, деленной на среднюю разность отсчетов:
После определения цены деления планиметра находят его постоянное число. Для этого обводят планиметром большой квадрат координатной сетки с известной площадью при полюсе внутри фигуры.
Постоянное число планиметра:
При передвижении счетного механизма вдоль обводного рычага изменяется его длина и соответственно изменяется цена деления и постоянное число планиметра. Длина обводного рычага точно фиксируется по шкале с делениями, нанесенными на рычаге.
При определении площадей планиметром необходимо соблюдать следующие правила:
— план или карта, по которому определяют площади, должен быть хорошо разглажен и натянут на ровном гладком столе;
— положение полюса планиметра выбирают так, чтобы при обводе данной фигуры не образовывались весьма острые или тупые углы между рычагами планиметра и чтобы счетное колесо при этом не сходило с листа бумаги;
— обводной шпиль следует вести по контуру плавно, выбирая все изгибы контура. Начальную точку выбирают в таком месте, в котором при обводе счетное колесо почти не вращается;
— для контроля и уточнения результатов каждый контур обводят два раза в прямом и обратном направлениях и берут среднее из результатов.
Точность определения площадей планиметром зависит от формы и размера обводимой фигуры, состояния плана и других причин. Для фигур средней величины (10–30 см 2 ) ошибка определения площади планиметром не превышает 1:200 величины площади.