Что такое среднее арифметическое 5 класса
Среднее арифметическое
Чтобы найти среднее арифметическое, нужно сложить все числа и поделить их сумму на их количество.
Обозначим среднее арифметическое буквой « m ». По определению выше найдем сумму всех чисел.
Разделим полученную сумму на количество взятых чисел. У нас по условию три числа.
В итоге мы получаем формулу среднего арифметического:
Для чего нужно среднее арифметическое?
Кроме того, что его постоянно предлагают найти на уроках, нахождение среднего арифметического весьма полезно и в жизни.
Например, вы решили продавать футбольные мячи. Но так как вы новичок в этом деле, совершенно непонятно по какой цене вам продавать мячи.
Тогда вы решаете узнать, по какой цене в вашем районе уже продают футбольные мячи конкуренты. Узнаем цены в магазинах и составим таблицу.
| Магазин | Цена футбольного мяча |
|---|---|
| «Спорт-товары» | 290 руб. |
| «Adidas» | 360 руб. |
| «Все для футбола» | 310 руб. |
Цены на мячи в магазинах оказались совсем разные. Какую цену для продажи футбольного мяча нам лучше выбрать?
Если выбрать самую низкую ( 290 руб.), то мы будем продавать товар себе в убыток. Если выбрать самую высокую ( 360 руб.), то покупатели не будут приобретать футбольные мячи у нас.
Нам нужна средняя цена. Здесь на помощь приходит среднее арифметическое.
Вычислим среднее арифметическое цен на футбольные мячи:
Таким образом, мы получили среднюю цену ( 320 руб.), по которой мы можем продавать футбольный мяч не слишком дёшево и не слишком дорого.
Средняя скорость движения
Со средним арифметическим тесно связано понятие средней скорости движения.
Наблюдая за движением транспорта в городе, можно заметить, что машины, то разгоняются и едут с большой скоростью, то замедляются и едут с маленькой скоростью.
Таких участков на пути следования автотранспорта бывает много. Поэтому для удобства расчётов, используют понятие средней скорости движения.
Средняя скорость движения — это весь пройденный путь разделить на всё время движения.
Рассмотрим задачу на среднюю скорость.
Задача № 1503 из учебника «Виленкин 5 класс»
Автомобиль двигался 3,2 ч по шоссе со скоростью 90 км/ч, затем 1,5 ч по грунтовой дороге со скоростью 45 км/ч, наконец 0,3 ч по просёлочной дороге со скоростью 30 км/ч. Найдите среднюю скорость движения автомобиля на всём пути.
Для расчёта средней скорости движения нужно знать весь путь, пройденный автомобилем, и всё время, которое автомобиль двигался.
S1 = 90 · 3,2 = 288 (км) — шоссе.
S2 = 45 · 1,5 = 67,5 (км) — грунтовая дорога.
S3 = 30 · 0,3 = 9 (км) — просёлочная дорога.
S = 288 + 67,5 + 9 = 364,5 (км) — весь путь, пройденный автомобилем.
t = 3,2 + 1,5 + 0,3 = 5 (ч) — всё время.
Vср = 364,5 : 5 = 72,9 (км/ч) — средняя скорость движения автомобиля.
Ответ: Vср = 72,9 (км/ч) — средняя скорость движения автомобиля.
Простая формула, чтобы подсчитать среднее арифметическое
Понятие среднего арифметического
Среднее арифметическое нескольких чисел — это сумма этих чисел, которую разделили на количество слагаемых. Формула среднего арифметического, которую обычно проходят в 5 классе, выглядит так:
Потренируемся использовать формулу среднего арифметического.
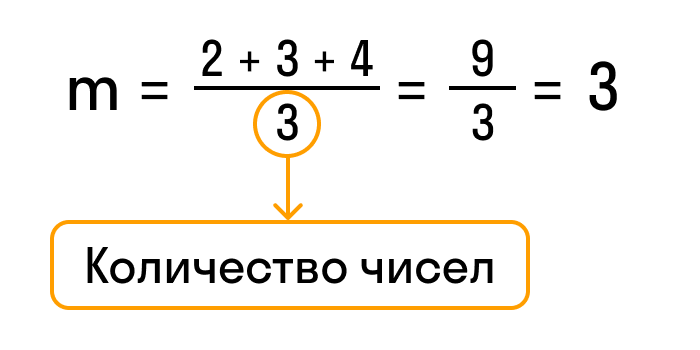
Например, найдем среднее арифметическое чисел 2, 3 и 4. Обозначим среднее значение латинской буквой «m» и посчитаем сумму этих чисел.
Разделим результат на количество чисел в задании, то есть на 3, и получим ответ — 3.
Применить эти знания можно в любой сфере жизни, где нужно обобщить и дать среднюю оценку: узнать среднюю цену товара в разных магазинах, вычислить среднюю зарплату сотрудников компании, сравнить среднюю посещаемость занятий учениками 5А и 5Б.
Средняя скорость движения — это весь пройденный путь, поделенный на время движения. Формула:
Так мы рассмотрели самые основные методы нахождения среднего значения. Теперь осталось попрактиковаться на примерах, чтобы быстро решать задачки на контрольной.
Примеры расчета среднего арифметического
Пример 1. Вычислить среднее арифметическое 33,3 и 55,5.
Чтобы найти среднее арифметическое двух чисел, надо сложить эти числа и результат разделить на 2: (33,3 + 55,5) : 2 = 88,8 : 2 = 44,4.
Пример 2. Подсчитать среднее арифметическое 7,5 и 8 и 0,5.
Чтобы найти среднее арифметическое трех чисел, надо сложить эти числа и результат разделить на 3: (7,5 + 8 + 0,5) : 3 = 16 : 3 = 5,33.
Пример 3. Найти среднее арифметическое 202, 105, 67 и 9.
Чтобы найти среднее арифметическое четырех чисел, надо сложить эти числа и результат разделить на 4: (202 + 105 + 67 + 9) : 4 = 383 : 4 = 95,75.
Пример 4. Сколько в среднем тратит школьник денег в неделю, если в понедельник он потратил 80 рублей, во вторник 75 рублей, в среду и четверг по 100 рублей, в пятницу 50 рублей.
Чтобы найти сколько в среднем школьник потратил за пять дней, надо сложить эти суммы и результат разделить на 5: (80 + 75 + 100 + 100 + 50) : 5 = 405 : 5 = 81.
Ответ: школьник в неделю тратит в среднем 81 рубль.
Еще больше интересных практических заданий — на курсах математики в онлайн-школе Skysmart. Вводный урок — бесплатно!
Среднее арифметическое
Среднее арифметическое – это частное от деления суммы чисел на их количество.
Пример 1. Найти среднее арифметическое двух чисел: 4 и 6.
Решение: Сначала найдём сумму данных чисел:
Затем разделим полученный результат на количество слагаемых, то есть на 2:
Значит среднее арифметическое двух чисел (4 и 6) равно 5.
Пример 2. Найти среднее арифметическое чисел 15, 8, 20 и 13.
Решение: Сначала найдём сумму данных чисел:
Затем разделим полученный результат на количество слагаемых:
Из данных примеров можно сделать вывод, что для нахождения среднего арифметического, нужно сложить все числа и поделить их сумму на их количество.
Рассмотрим задачи, в которых требуется найти средне арифметическое нескольких чисел, относящихся к одной величине.
Задача 1. Утром температура была 15 градусов, днём она поднялась до 27 градусов, а вечером опустилась до 19, ночью температура достигла отметки в 11 градусов. Найти среднюю температуру за сутки.
Решение: Сначала найдём общую сумму температур за сутки:
15 + 27 + 19 + 11 = 72,
затем разделим полученную сумму на 4:
Ответ: средняя температура за сутки равна 18 градусам.
Задача 2. В магазине продали 6 килограммов яблок по цене 55 рублей за килограмм и 4 килограмма груш по цене 75 рублей за килограмм. Какая средняя цена 1 килограмма фруктов?
Решение: Сначала посчитаем сколько всего денег получил магазин за фрукты:
55 · 6 = 330 (р) — выручка за яблоки;
75 · 4 = 300 (р) — выручка за груши;
330 + 300 = 630 (р) — общая выручка за фрукты.
Затем найдём общий вес фруктов:
теперь разделим общую выручку на общий вес проданных фруктов и получим среднюю цену за 1 кг:
Ответ: средняя цена 1 килограмма проданных фруктов — 63 рубля.
«Среднее арифметическое». Урок математики в 5-м классе
Разделы: Математика
Тема урока: «Среднее арифметическое».
Класс: 5.
Тип урока: урок изучения нового материала.
Вид урока: мультимедийный урок.
Оборудование:мультимедийный проектор, слайды, созданные в программе Microsoft Power Point (Приложение), доска.
Эпиграф к уроку:Чем больше я знаю, тем больше умею.
I. Организационный момент
II. Устная работа
(Начинается демонстрация слайда )
а) 0,14 + 0,06; б) 2,78 + 5,22;
в) 3,7 + 1,13; г) 4 + 0,4;
д) 1,45 + 0,5; е) 16,3 + 3,07.
а) 0,42 : 7; б) 4,08 : 0,04;
в) 50 : 0,5; г) 0,18 : 0,6;
д) 1 : 0,2; е) 6 : 0,03.
III. Изучение нового материала
Учитель.Ребята, сегодня мы изучим новую тему. Называется она «Среднее арифметическое». Запишем число и тему урока.
(Демонстрируется слайд 2).
(Начинается демонстрация слайда 3). Рассмотрим задачу: У Ани 14 конфет, у Кати 9 конфет, а у Оли 10 конфет. Сколько конфет достанется каждой девочке, если конфеты разделить между ними поровну? Решение обсуждается с учащимися.
14 + 9 + 10 = 33 (конфеты)
33 : 3 = 11 (конфет)
Число 11 называют средним арифметическим чисел 14; 9 и 10.
Рассмотрим еще задачу (демонстрируется слайд 4): Миша, Петя и Коля были в походе. Подойдя к лесу, они решили сделать привал. У Миши было 2 пирожка, у Пети 4 и у Коли 6. Все пирожки мальчики разделили поровну и съели. Сколько пирожков съел каждый?
Совместно с учащимися получается:
2 + 4 + 6 = 12 (пирожков)
12 : 3 = 4 (пирожка)
Число 4 называется средним арифметическим чисел 2; 4 и 6.
Ребята, что же называется средним арифметическим чисел? ( Ответы учащихся)
(Далее демонстрируется слайд 5)
Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на число слагаемых.
Как найти среднее арифметическое нескольких чисел? (Ответы ребят)
(Слайд 6)
Среднее арифметическое = (Сумма чисел) : (количество слагаемых)
(Учащиеся записывают в тетрадях)
IV. Закрепление изученного материала
Ребята, давайте закрепим наши знания, решаем номер № 1497 (б, в). (Начинается демонстрация слайда 7).
№ 1497 (б) решается совместно с учителем.
0,1 + 0,2 + 0,3 = 0,6
0,6 : 3 = 0,2
Можно писать короче: (0,1 + 0,2 + 0,3) : 3 = 0,2. Пишем ответ.
Ответ: 0,2.
№ 1497 (в) – у доски
№ 1502 – у доски
(5,3 + 5,4 + 4,8 + 5,0 + 5,3 + 5,4 + 5,3 + 5,2 + 5,1) : 9 = 46,8 : 9 = 5,2
Ответ: 5,2.
Физкультминутка
Поднимает руки класс – это «раз».
Повернулась голова – это «два».
Руки вниз, вперед смотри – это «три».
Руки в стороны пошире развернули на «четыре»,
С силой их к плечам прижать – это «пять».
Всем ребятам надо сесть – это «шесть».
(Демонстрируется слайд 8)
1) Найти среднее арифметическое первых пяти натуральных чисел.
Вспоминаем какие числа называются натуральными. Решают самостоятельно.
(1 + 2 + 3 + 4 + 5) : 5 = 15 : 5 = 3. Ответ: 3.
2) Сумма пяти чисел 20,5. Каково среднее арифметическое этих чисел?
После обсуждения решают самостоятельно.
20,5 : 5 = 4,1. Ответ: 4,1.
3). Утром температура воздуха была 15,3 °С, в полдень 23,4 °С, а вечером 17,1 °С. Вычислить среднюю температуру воздуха за этот день.
V. Задание на дом: № 1525, 1528* (для сильных) (Слайд 9)
VI. Итог урока. Выставление оценок
– Что мы сегодня узнали нового на уроке?
– Что мы научились делать?
Среднее арифметическое
Содержание
Возможно, вы слышали выражения «средний балл за контрольную», «среднее количество осадков» или «средняя годовая температура». Этот урок посвящён среднему арифметическому – тому, что это такое, как находится и где может пригодиться.
Знакомство со средним арифметическим
То число грибов, которое получилось у каждого из друзей, будет средним арифметическим.
Среднее арифметическое нескольких чисел – это сумма этих чисел, разделённая на количество слагаемых.
Задачи на нахождение среднего арифметического
Теперь разделим эту сумму расстояний на количество часов.
Рассмотрим другую задачу.
Теперь просто вычтем из этого числа то, что делают первые двое рабочих и найдём количество деталей, которые делает третий.
$$(50 + 44 + 20) : 3 = 114 : 3 = 38$$
Среднее арифметическое десятичных дробей
Решать задачи на среднее арифметическое достаточно просто, если речь идёт о натуральных числах. Ненамного сложнее дело обстоит с десятичными дробями.
Сложим длины отрезков АВ и CD и вычислим их среднюю длину.
Вычислим, сколько съел каждый из кроликов.
Сначала найдём значение выражения.
$$1.4 \cdot x + x = 2.4 \cdot x = 15$$
Мы получили число моркови, которую съел белый кролик. Теперь давайте определим, сколько съел серый.
Проверим наше решение, сложив количество съеденного обоими кроликами и найдя среднее арифметическое.
Значит, наше решение было верным.
Среднее арифметическое обыкновенных дробей
Вычислять среднее арифметическое обыкновенных дробей приходится не так уж часто. Но давайте рассмотрим, как это делается.
Особенность поиска среднего арифметического обыкновенных дробей состоит в том, что нужно складывать их, а, значит, приводить к общему знаменателю.
Напомним, что приведение к общему знаменателю основывается на основном свойстве дроби, которое позволяет умножить обе части дроби на одно и то же число без изменения значения. Таким образом, мы можем найти для дробных слагаемых дополнительные множители, с помощью которых знаменатели слагаемых станут одинаковыми.
Умножаем обе части дроби на один и тот же дополнительный множитель.
Теперь у нас две дроби с одинаковым знаменателем, и мы можем легко их сложить.
Осталось только разделить эту сумму на число слагаемых. При делении обыкновенной дроби нужно умножить знаменатель дроби на делитель:
Многие операции, которые мы разобрали подробно, можно сделать и устно – здесь они расписаны так только для того, чтобы немного повторить пройденный материал.
Сначала нужно перевести каждую из этих смешанные дробей в неправильную. Для этого нужно умножить целое число на знаменатель и прибавить числитель.
Теперь подбираем дополнительные множители и складываем наши дроби.
Но если в условиях не сказано, что нужна именно десятичная дробь, лучше оставить обыкновенную, так как она будет точно передавать значение выражения.